Projektowanie elementów zginanych wg

Eurokodu 2

Część 2 – Obliczenia według metody

uproszczonej

WYKŁAD NR 3

PODSTAWY

PROJEKTOWANIA

KONSTRUKCJI

ŻELBETOWYCH

Semestr V , r .ak. 2011/2012

Opracowanie - prof. dr hab. inż. Andrzej Łapko

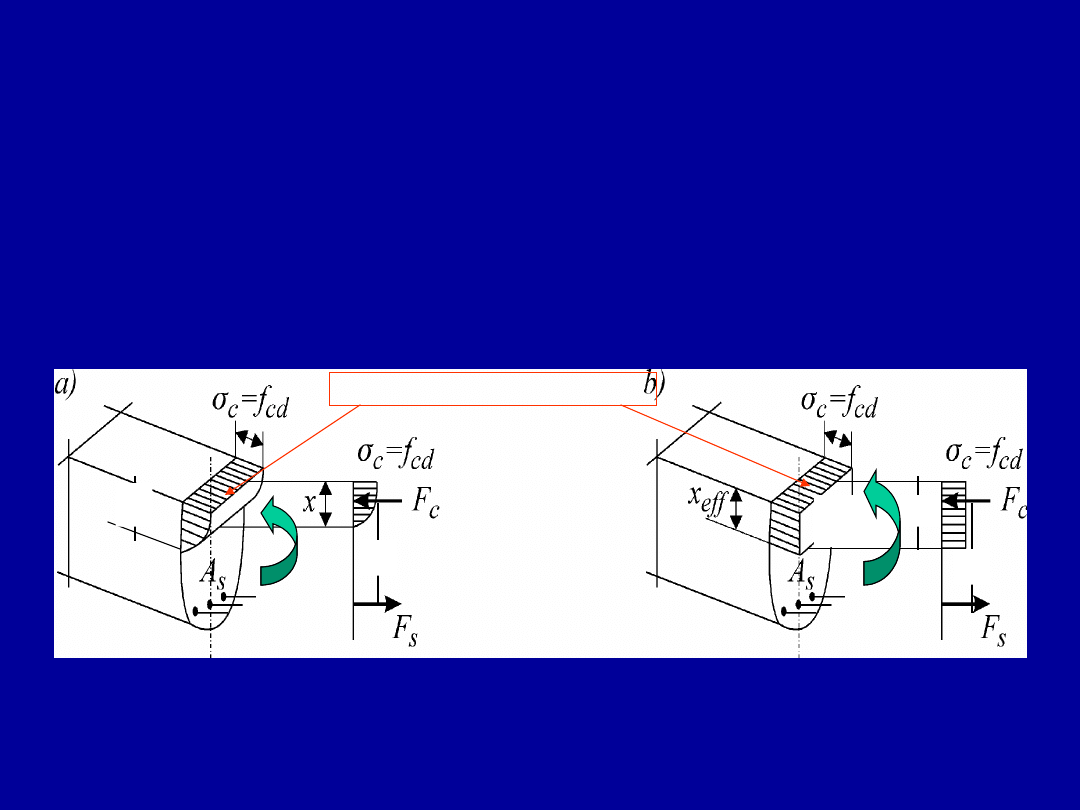
Podejścia przy określaniu nośności

przekrojów

w elementach zginanych

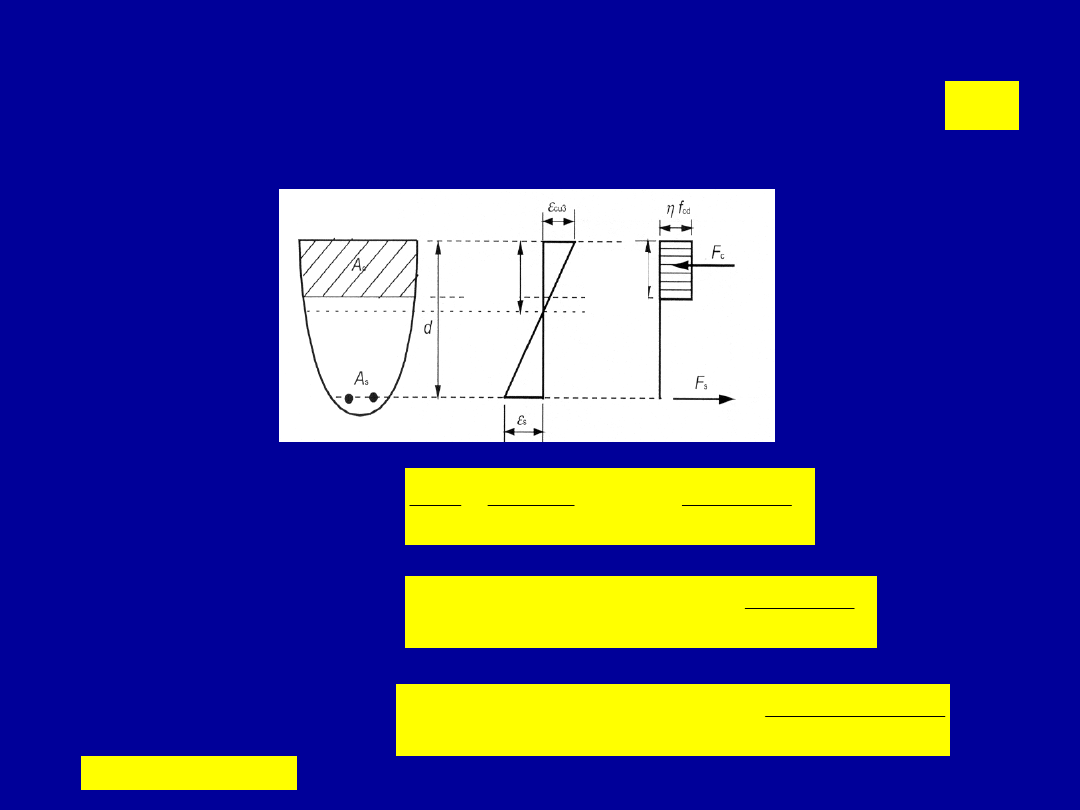
Podejścia przy analizie przekrojów zginanych

a) – ogólne, b) - uproszczone

Do sprawdzania SGN i wymiarowania żelbetowych

przekrojów w elementach zginanych można

wykorzystywać dwa podejścia:

1. Ogólne, 2. Uproszczone

M

Rd

M

Rd

x

ef

x

z

c

z

c

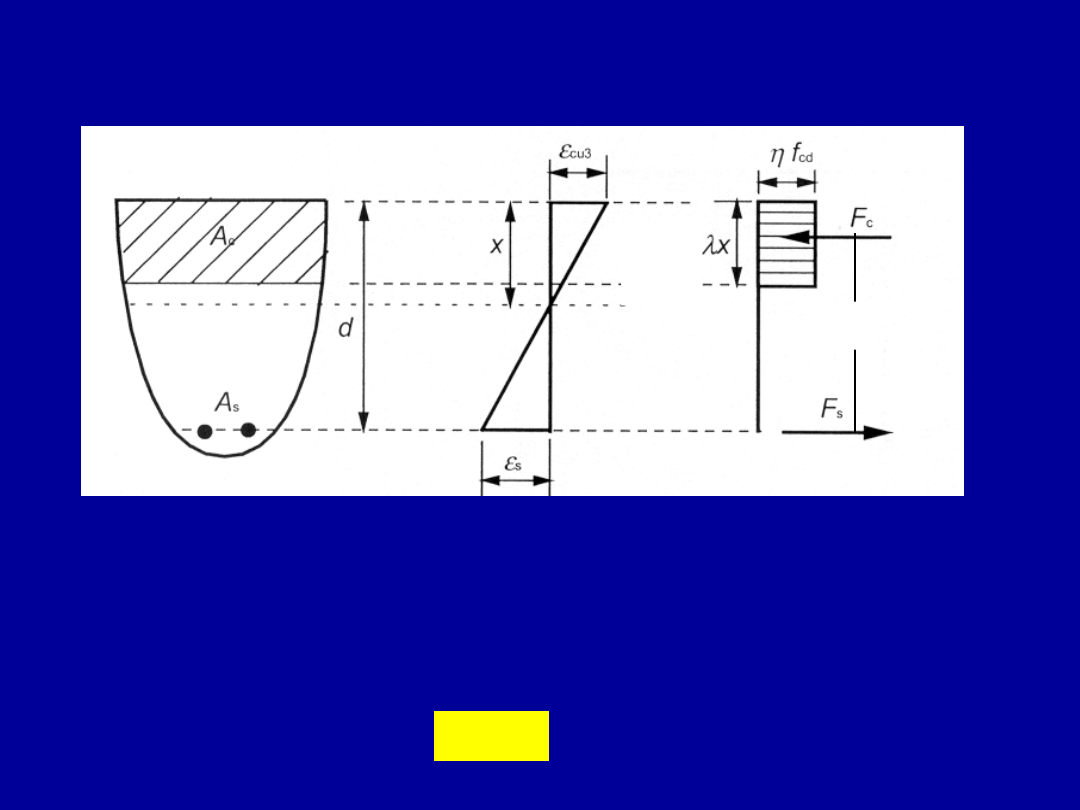
Blok naprężeń w strefie ściskanej

3

Metoda uproszczona – założenia

Na podstawie stanu odkształcenia przekroju ustala się
wyłącznie graniczną
wysokość strefy ściskanej, która wynika z przyjęcia
granicznych odkształceń



c

= ε

cu3

[‰] w betonie oraz odkształceń



sy

= w zbrojeniu

rozciąganym.

Uproszczenie – wykres prostokątny naprężeń w strefie ściskanej
o zasięgu efektywnym

x

x

ef







x

ef

=

z

c

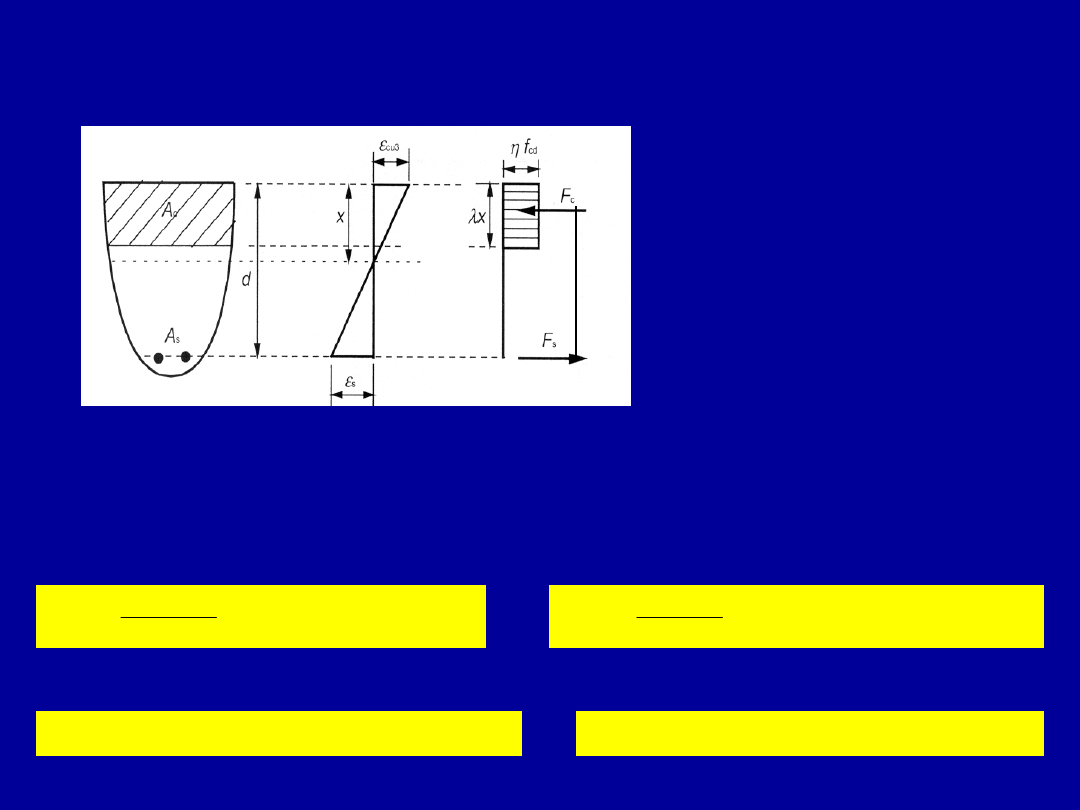
Metoda uproszczona – założenia wg PN-EN

Uproszczenie – dla betonów zwykłych zasięg strefy
ściskanej
opisuje współczynnik λ, a stan naprężeń w skrajnym
włóknie - η

x

ef

=

z

c

50MPa

f

dla

0,8

λ

ck





MPa

90

f

50

dla

400

50)

(f

-

0.8

λ

ck

ck









MPa

50

f

dla

1,0

η

ck





MPa

90

f

50

dla

200

50

f

-

1,0

η

ck

ck









Betony wszystkich klas

Betony zwykłe klas do C50/60

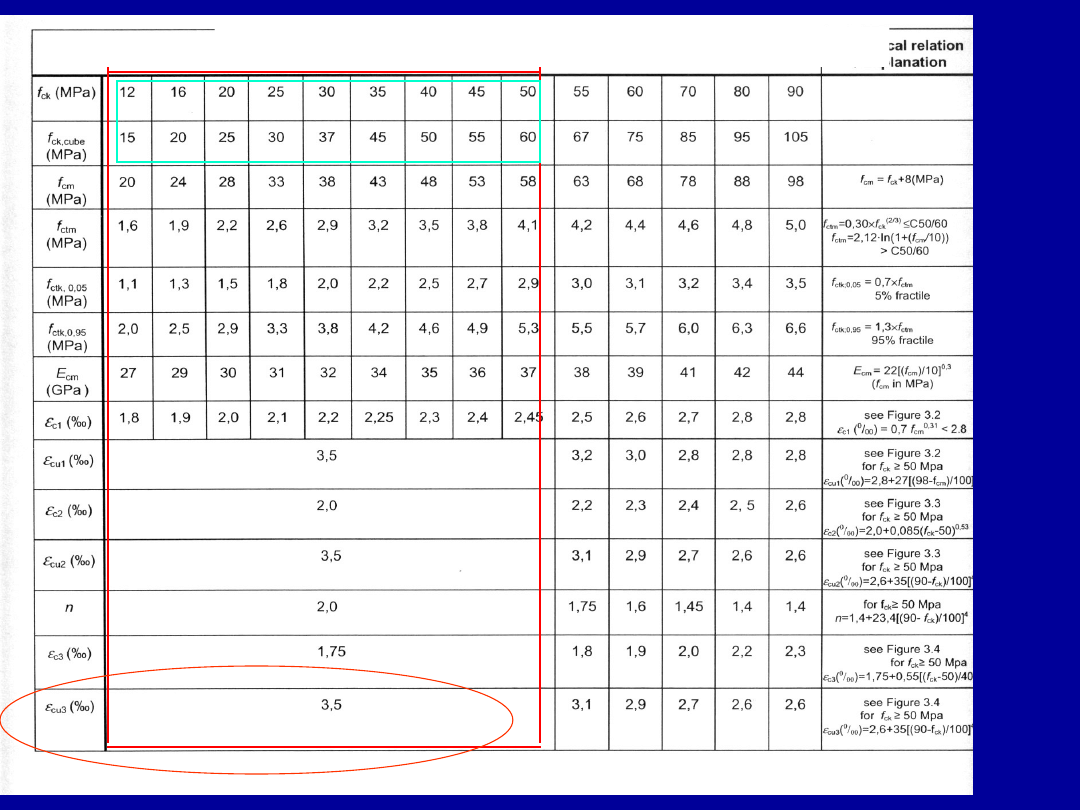
5

Charakterystyka klas betonu według Eurokodu 2

Graniczny zasięg strefy ściskanej w

elemencie zginanym z betonu zwykłych klas

d

x

x

d

x

sy

cu

cu

sy

cu





















3

3

lim

lim

lim

3

lim

,

ef

x

x

lim

x

ef,li

m

d

x

x

x

sy

cu

cu

ef

ef





















3

3

lim

,

lim

lim

,

W metodzie ogólnej

W metodzie uproszczonej
dla wszystkich betonów

W metodzie uproszczonej
dla betonów klas zwykłych

s

yd

ef

ef

E

f

d

x

x

x

/

0035

,

0

0035

,

0

8

,

0

8

.

0

lim

,

lim

lim

,













0035

,

0

,

8

,

0

3





cu





7

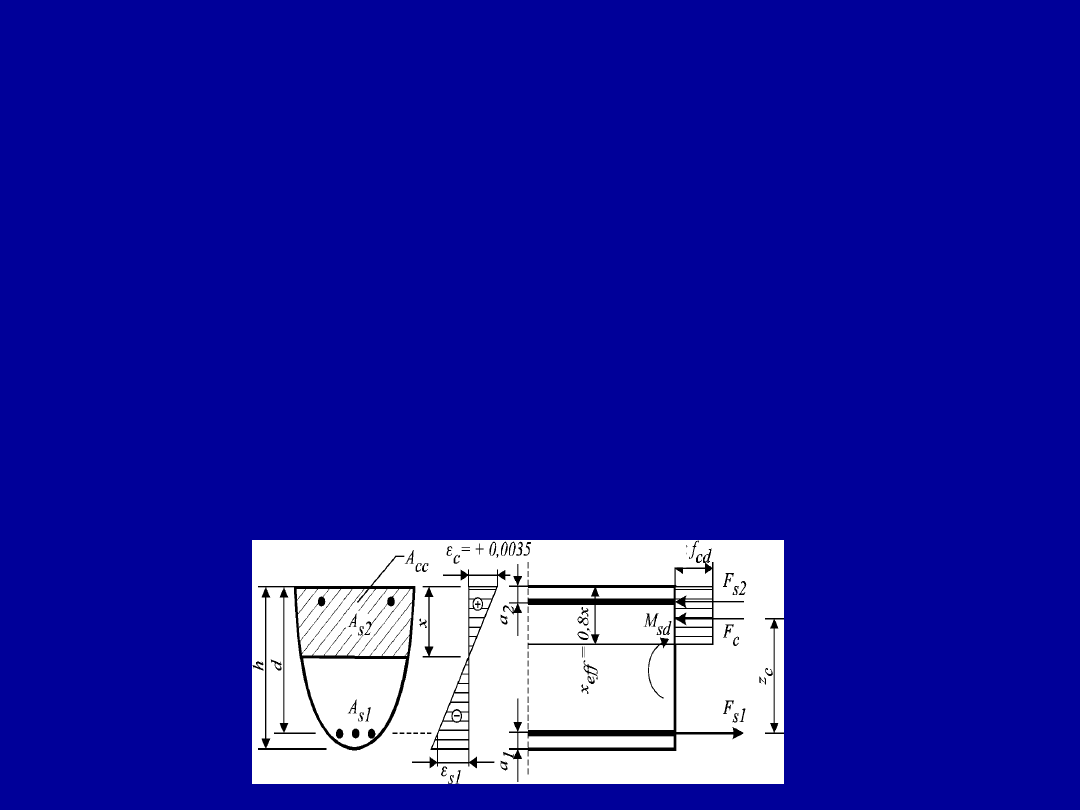
Graniczny zasięg strefy ściskanej w betonach

zwykłych klas

UWAGA !

Przekroczenie w obliczeniach zasięgu ξ

eff,lim

oznacza belkę przezbrojoną, w której stal rozciągana nie

osiąga granicy plastyczności (ε

y

< ε

sy

)

(jest to rozwiązanie nieekonomiczne).

lim

,

ef

x

Używamy zapisu w postaci bezwymiarowej ξ

ef

= x

ef

/d





















s

yd

ef

ef

E

f

d

x

/

0035

,

0

0035

,

0

8

,

0

lim

,

lim

,



x

lim

x

ef,li

m

Zapis dla betonów zwykłych

w postaci bezwymiarowej

ξ

ef,lim

= x

eflimf

/d

Przykład: dla stali gat. 34GS – f

yd

= 350 MPa, E

s

= 200 000 MPa

ξ

eff,lim

= 0,530

dla stali gat. RB 500 – f

yd

= 420 MPa, E

s

= 200 000 MPa

ξ

eff,lim

= 0,500

8

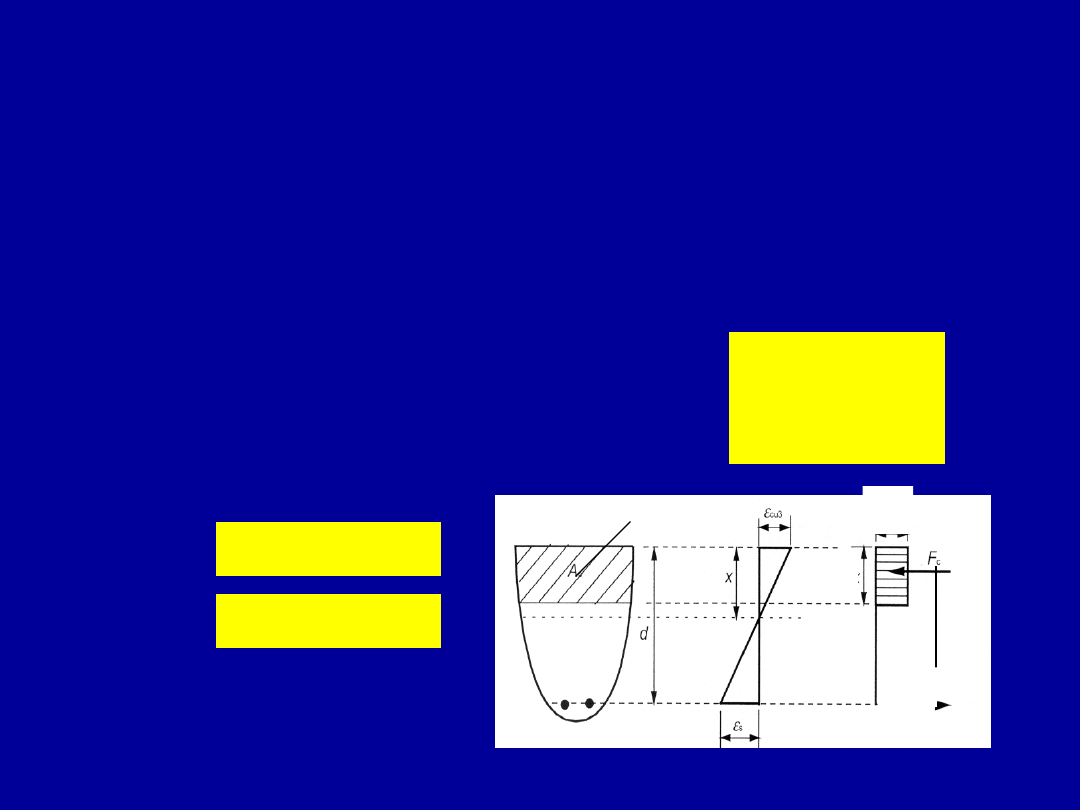
Beton zwykły - założenia metody

uproszczonej

Przekrój obciążony momentem zginającym obliczeniowym
M

Sd

pozostaje w równowadze pod działaniem

następujących sił wewnętrznych:

• wypadkowej naprężeń ściskających w betonie F

c

obliczanej na
podstawie prostokątnego wykresu naprężeń,
• wypadkowej F

s1

naprężeń w zbrojeniu rozciąganym,

• wypadkowej F

s2

naprężeń w zbrojeniu umieszczonym w

strefie
ściskanej,
• momentu wewnętrznego (nośności na zginanie) M

Rd

,

wynikającej
z działania pary sił: w strefie ściskanej i rozciąganej.

9

Równania równowagi dowolnego

przekroju zginanego, pojedynczo

zbrojonego

0

0

0

1

1













c

s

Ed

c

c

Ed

s

c

z

F

M

z

F

M

F

F

Suma rzutów sił na oś
podłużną

Suma momentów względem osi zbrojenia
rozciąganego

Suma momentów względem środka ciężkości
strefy ściskanej

gdzie:

cd

ef

cc

c

f

A

F

,



yd

s

s

f

A

F

1

1



A

cc,ef

f

cd

x

ef

F

s1

A

s1

10

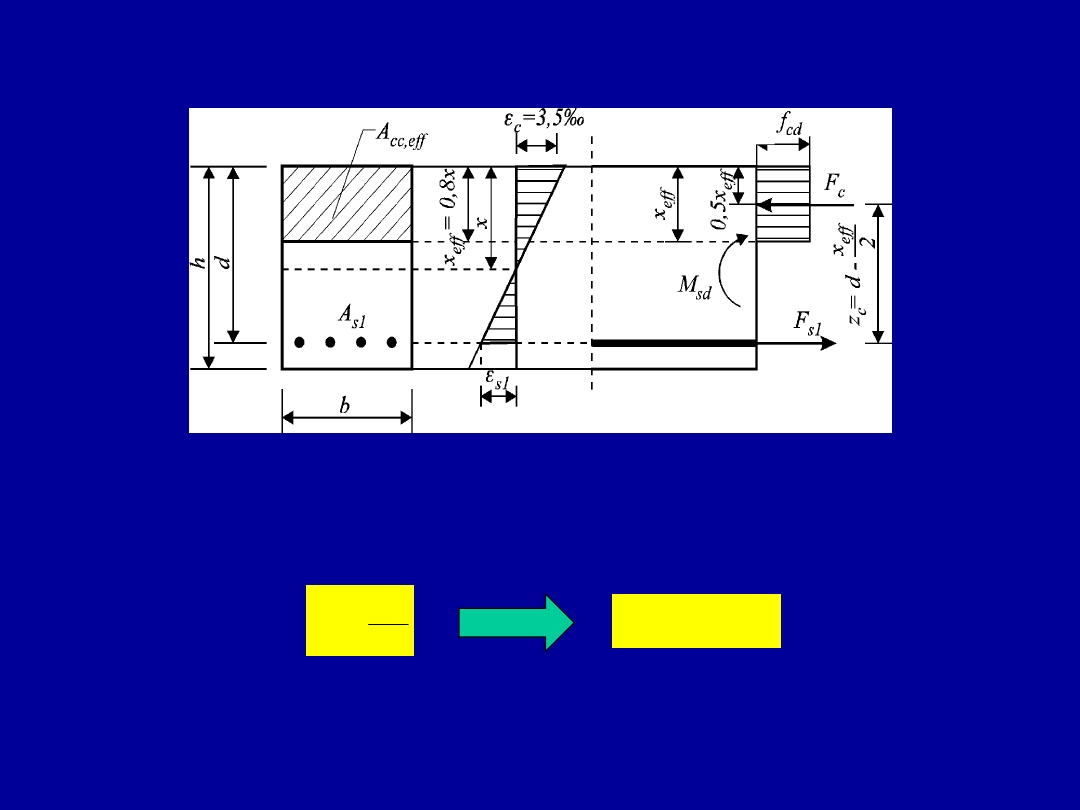
Przekrój prostokątny

pojedynczo zbrojony

z betonów klas do C50/60

11

Element pojedynczo zbrojony o przekroju prostokątnym

Położenie osi obojętnej x

ef

można wyrazić w sposób

bezwymiarowy

d

x

ef

ef





d

x

ef

ef







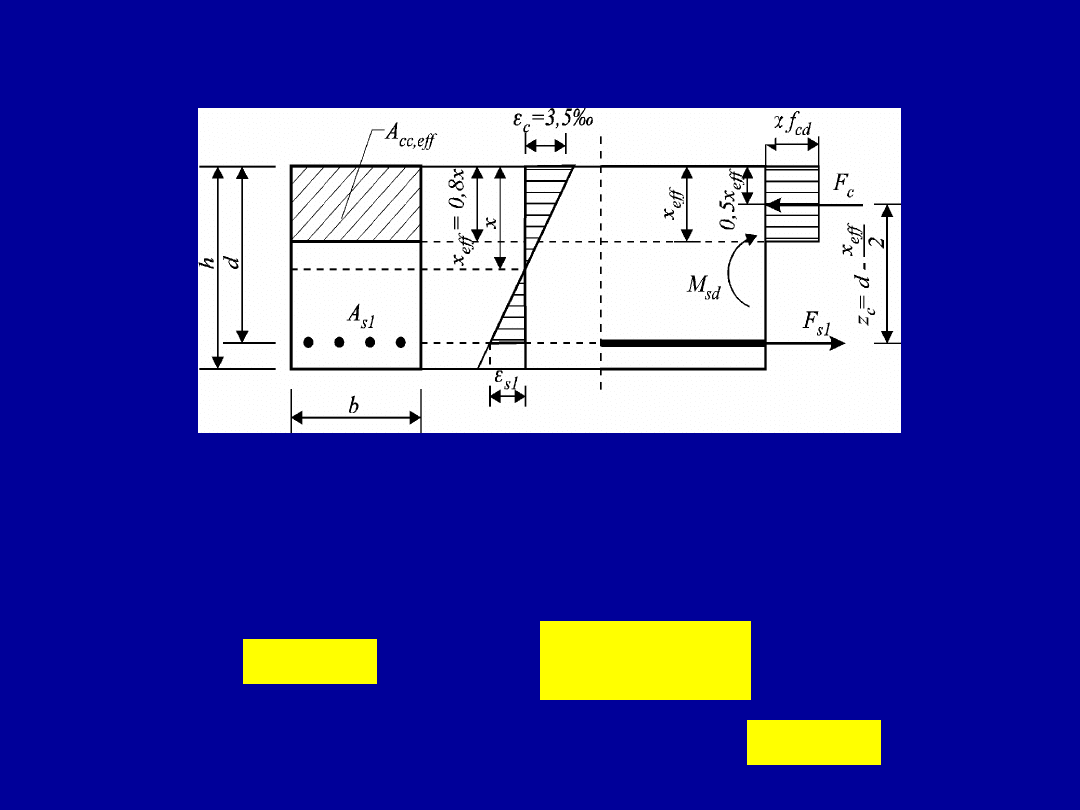
12

Element o przekroju prostokątnym pojedynczo zbrojonym

Pod działaniem momentu zginającego przekrój pozostaje
w równowadze pod działaniem następujących sił wypadkowych

:

• Wypadkowej ciśnień w strefie ściskanej betonu F

c

cd

ef

c

f

b

x

F 

• Wypadkowej naprężeń rozciągających w zbrojeniu

yd

s

s

f

A

F





1

1

cd

x

ef

c

f

b

d

F

ef















lub

13

Przekrój prostokątny pojedynczo zbrojony

W przekroju prostokątnym o stałej szerokości b wypadkowa

bloku naprężeń w strefie ściskanej położona jest w środku

ciężkości bryły naprężeń w odległości

2

2

d

x

a

ef

ef

c







Natomiast ramię sił wewnętrznych zapisane jest wzorem





















2

1

2

ef

ef

c

d

x

d

z



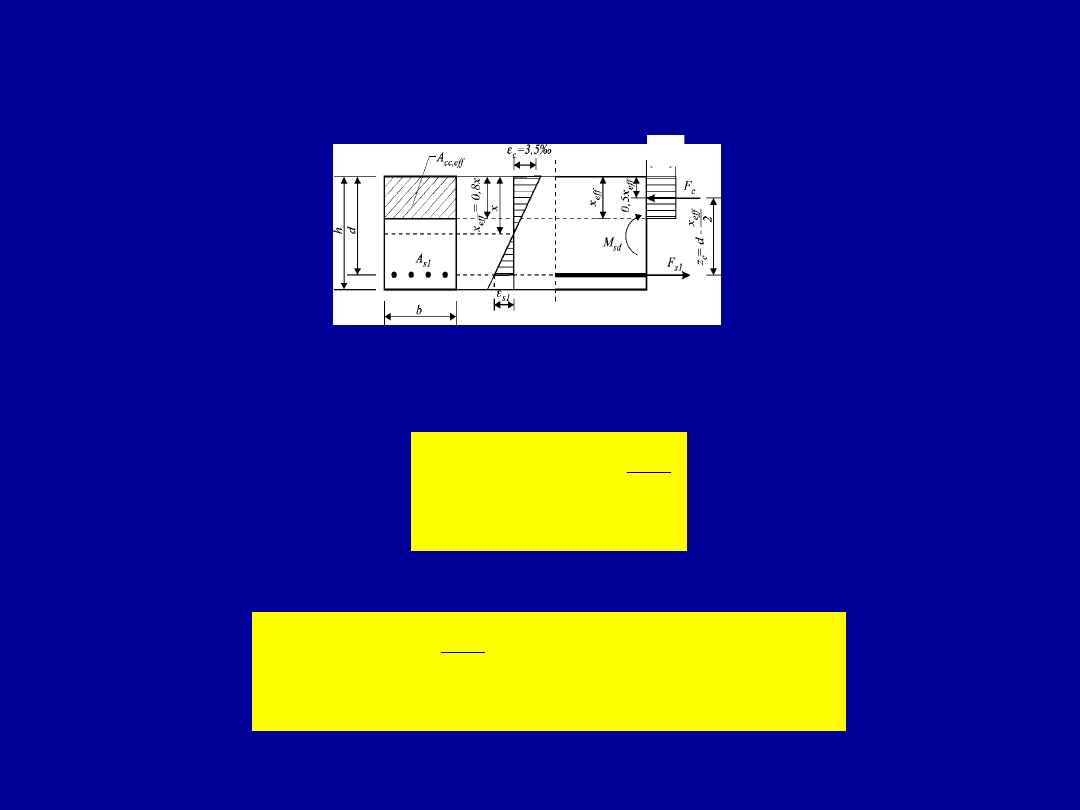
14

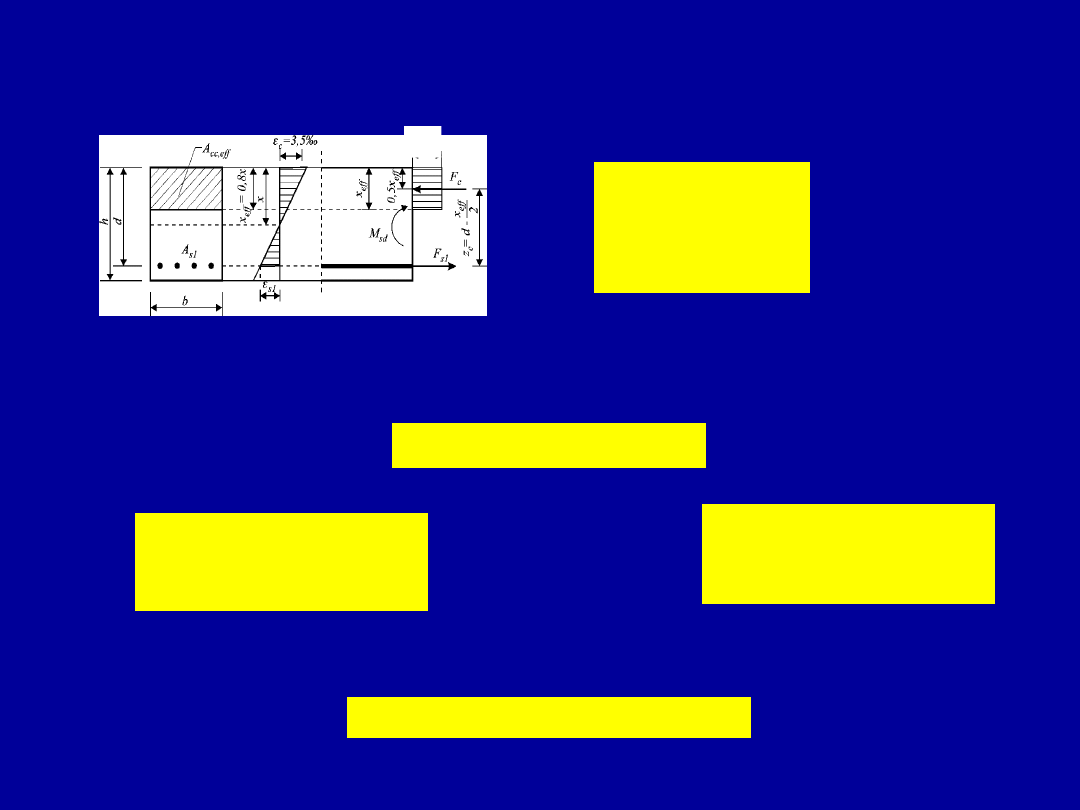
Nośność przekroju prostokątnego

pojedynczo zbrojonego

Moment sił wewnętrznych wynikający z działania pary sił F

c

i F

s1

, obliczony względem osi zbrojenia A

s1

ma postać.

Moment oznacza nośność na zginanie

 

 





 



c

c

z

ef

F

cd

ef

Rd

x

d

bf

x

M

















2

Moment sił wewnętrznych można też zapisać w postaci



cd

ef

cc

cd

S

c

ef

cc

cd

z

ef

A

ef

Rd

f

S

f

z

A

f

x

d

b

x

M

ef

cc

c

ef

cc

























,

,

,

,

2



 



 

 



gdzie: S

cc,ef

– moment statyczny powierzchni strefy ściskanej względem środka zbrojenia

f

cd

15

Równowaga przekroju prostokątnego

pojedynczo zbrojonego w elemencie

zginanym

f

cd

Warunek sumy rzutów sił na oś podłużną
elementu

1

1

0

s

c

s

c

F

F

F

F









0

1







yd

s

cd

x

ef

f

A

bf

d

ef











0

1

,







yd

s

cd

A

ef

f

A

f

b

x

ef

cc

lub

w

innej

postaci

Warunek równowagi momentów względem osi zbrojenia A

s1

c

c

Ed

Rd

Ed

z

F

M

M

M











0

0

0

0

1

1













c

s

Ed

c

c

Ed

s

c

z

F

M

z

F

M

F

F

Nośność na zginanie przekroju

prostokątnego

pojedynczo zbrojonego

Moment sił wewnętrznych wynikający z działania pary sił F

c

i F

s1

, obliczony względem osi zbrojenia A

s1

można zapisać w

funkcji bezwymiarowej x

ef

.

 

 





 



c

c

z

ef

F

cd

ef

Rd

x

d

bf

x

M

















2

cd

ef

ef

z

ef

F

cd

ef

Rd

bf

d

d

d

dbf

M

c

c

2

2

1

2









































 

 





 



d

x

d

x

ef

ef

ef

ef











Wykorzystując równanie równowago momentów otrzymujemy

cd

ef

ef

Ed

Rd

bf

d

M

M

2

2

1

























17



Obliczanie zbrojenia przekroju

prostokątnego pojedynczo

zbrojonego

Przyjmujemy wstępnie wymiary b x h przekroju zginanego
momentem o wartości obliczeniowej M

ed.

i zakładamy klasę

betonu i stali zbrojeniowej.
Obliczenia zbrojenia można być przeprowadzone analitycznie
Przekształcając

równanie

równowagi

momentów

można

obliczeniowo określić zasięg



ef

strefy ściskanej

ef

cd

Ed

ef

ef

f

bd

M















0

2

2

2

2

Po obliczeniu wartości



ef

potrzebne pole przekroju zbrojenia rozciąganego A

s1

można obliczyć z warunków równowagi sił na oś podłużną belki:

yd

cd

ef

s

f

f

db

A







1

stąd

cd

ef

ef

Ed

Rd

bf

d

M

M

2

2

1

























1

1

0

s

c

s

c

F

F

F

F









0

1





yd

s

cd

ef

f

A

dbf



18

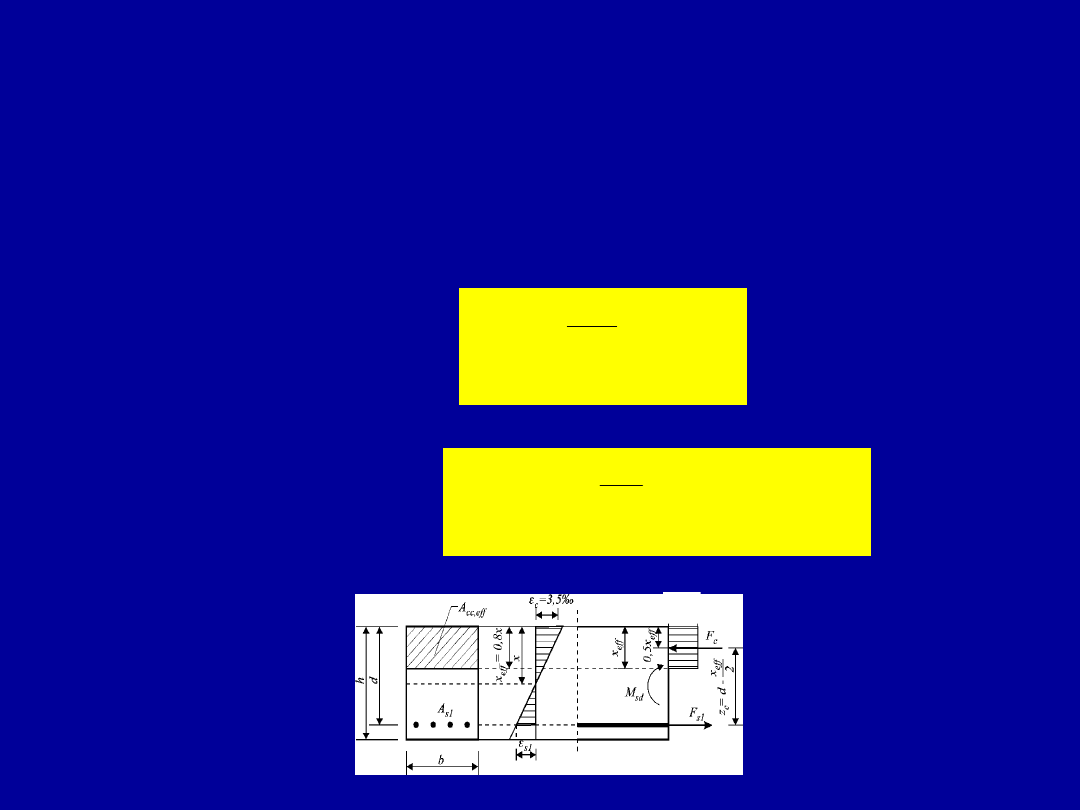
 Obliczanie zbrojenia przekroju

prostokątnego pojedynczo

zbrojonego

Pole zbrojenia można też wyznaczyć przekształcając równanie
równowagi momentów zewnętrznego i wewnętrznego

Pamiętając, że

stąd

yd

ef

Ed

s

f

d

M

A

















2

1

1



yd

c

Ed

s

c

F

yd

s

Ed

f

z

M

A

z

f

A

M

s











1

1

0

1



 



d

z

ef

c

















2

1



19

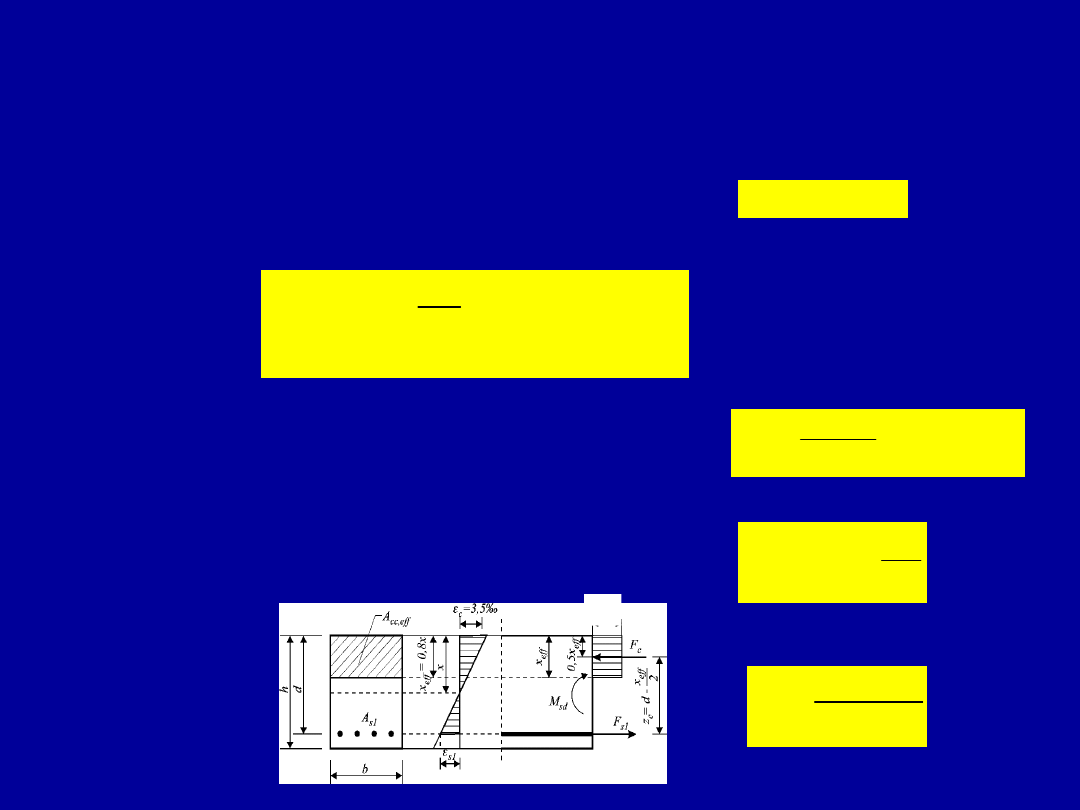
Projektowanie przekroju prostokątnego

pojedynczo zbrojonego przy użyciu tablic

Stabelaryzowane funkcje

pomocnicze



eff

= x

eff

/d,



eff

= f(



eff

)

oraz



eff

=

f(



eff

).

Ramię sił wewnętrznych z

c

d

d

z

ef

ef

c

ef



























 



2

1

Moment sił wewnętrznych

cd

ef

cd

ef

ef

Rd

bf

d

bf

d

M

ef

2

2

2

1

































 



 



f

cd

20

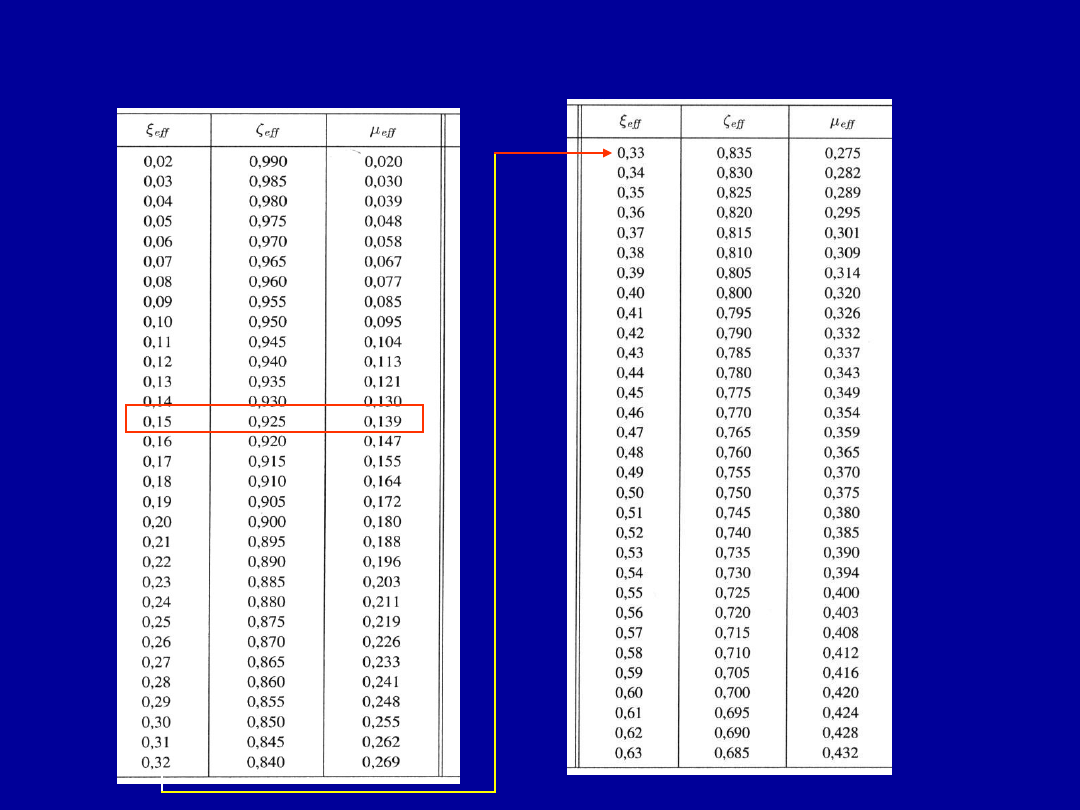
Projektowanie zbrojenia przekroju

prostokątnego pojedynczo zbrojonego przy

użyciu tablic

Z równania równowagi momentów sił wewnętrznych

f

cd

0





Rd

Sd

M

M

Możemy wyznaczyć współczynnik pomocniczy



eff

ef

ef

cd

Ed

ef

f

bd

M







lub

2





Pole przekroju zbrojenia rozciąganego wynosi

yd

cd

ef

s

f

f

db

A







1

lub

yd

ef

sd

s

f

d

M

A





1

cd

ef

cd

ef

ef

Rd

bf

d

bf

d

M

ef

2

2

2

1

































 



 



21

Tablice współczynników do projektowania elementu zginanego o przekroju prostokątnym

22

Korekta wyniku obliczeń z uwagi

na

minimalny stopień zbrojenia

bd

f

f

A

yk

ctm

s

26

,

0

min

,

1



bd

A

s

0013

,

0

min

,

1



gdzie: b – średnia szerokość strefy rozciąganej w elemencie,

d – wysokość użyteczna przekroju,
f

ctm

– średnia wytrzymałość betonu na rozciąganie

f

yk

– charakterystyczna granica plastyczności stali.

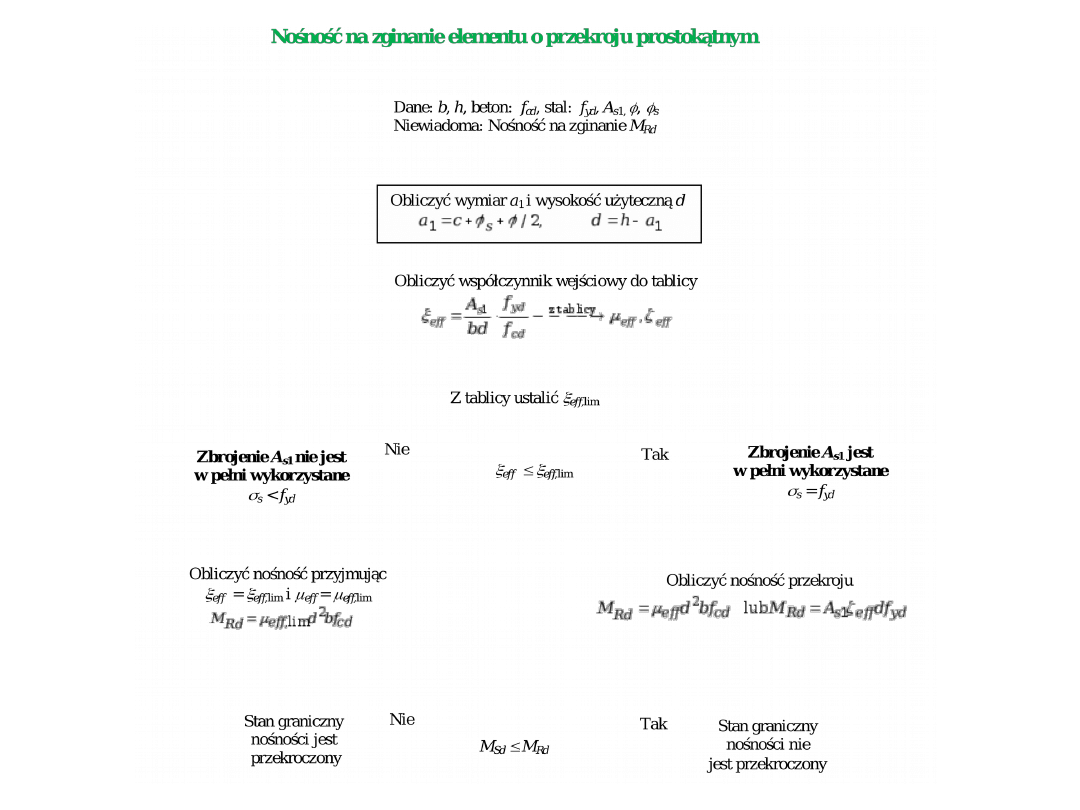
 Sprawdzanie nośności przekroju

zginanego

Nośność, czyli moment sił wewnętrznych elementu żelbetowego
określamy w celu sprawdzenia, czy stan graniczny nośności na
zginanie nie jest przekroczony. Znamy wymiary przekroju b x h
oraz pole powierzchni i układ zbrojenia i klasę betonu i stali
zbrojeniowej (wartości f

cd

oraz f

yd

).

Z tablicy ustalamy wartość współczynnika



ef

,i określamy nośność na zginanie

Stan graniczny nośności sprawdzamy z warunku SGN:

Na podstawie równania równowagi sił określamy współczynnik tablicowy ξ

ef

cd

yd

s

ef

f

f

bd

A

1





0

1





yd

s

cd

ef

f

A

dbf



cd

ef

Rd

bf

d

M

2





Rd

Ed

M

M



24

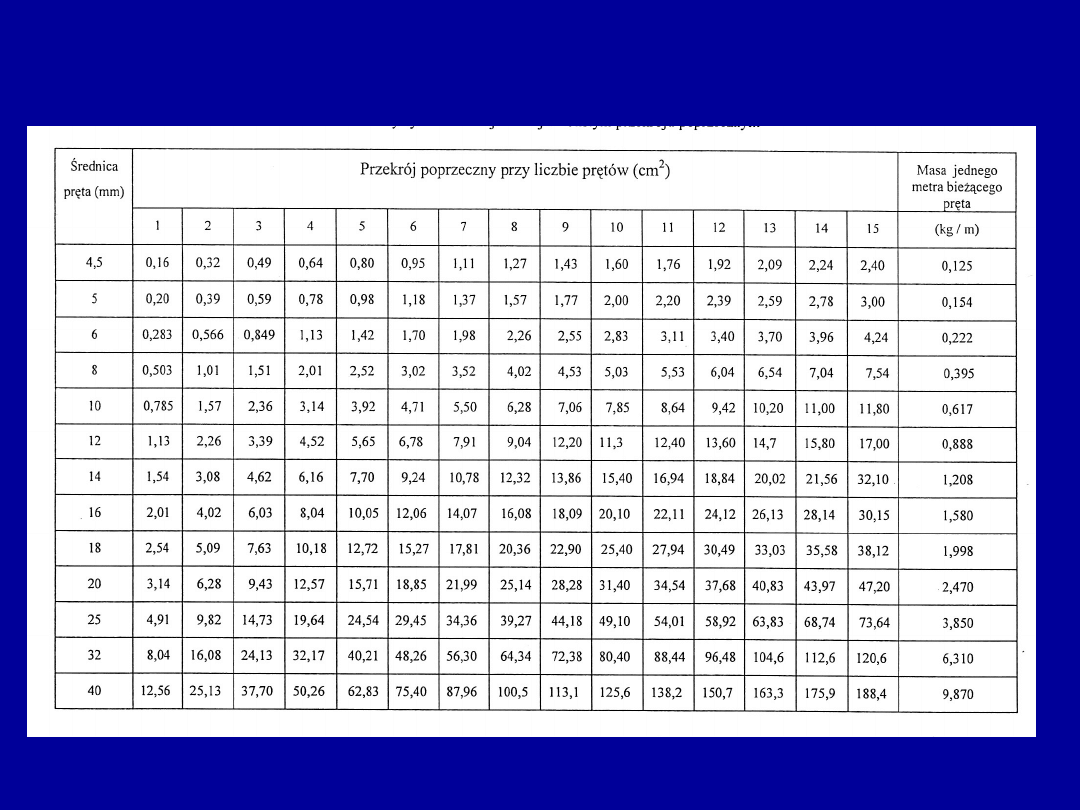
Tablica doboru prętów zbrojenia

26

Korekta wyniku obliczeń

zbrojenia z uwagi na minimalny

stopień zbrojenia

bd

f

f

A

yk

ctm

s

26

,

0

min

,

1



bd

A

s

0013

,

0

min

,

1



gdzie: b – średnia szerokość strefy rozciąganej w elemencie,

d – wysokość użyteczna przekroju,
f

ctm

– średnia wytrzymałość betonu na rozciąganie

f

yk

– charakterystyczna granica plastyczności stali.

27

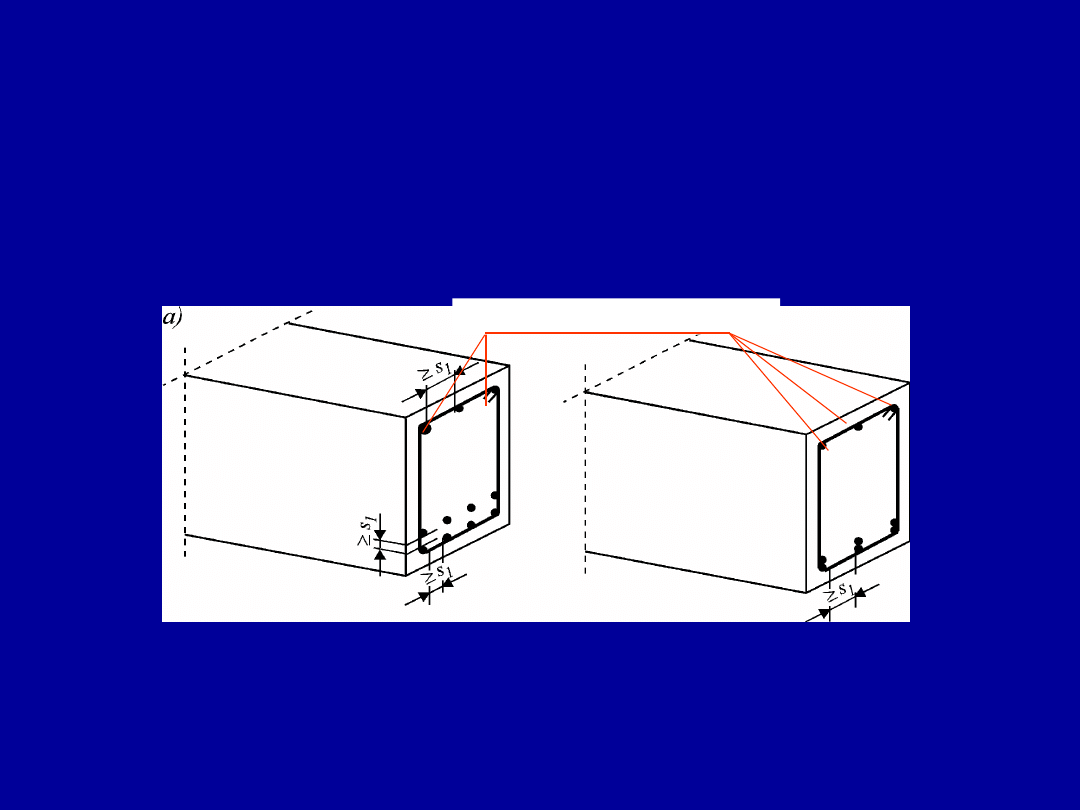
Element zginany o przekrój

prostokątnym

podwójnie zbrojonym – betony

zwykłe

Zbrojenie w strefie ściskanej

28

Przekrój prostokątny podwójnie

zbrojony

Przypadki zastosowania podwójnego zbrojenia:

1. Nośność strefy ściskanej nie jest wystarczająca, tzn.

lim

,

ef

ef







2.

Na belkę działają momenty różnych znaków, tzn. +M

Ed

i - M

Ed

3. Belka wymaga zbrojenia ze względów konstrukcyjnych

29

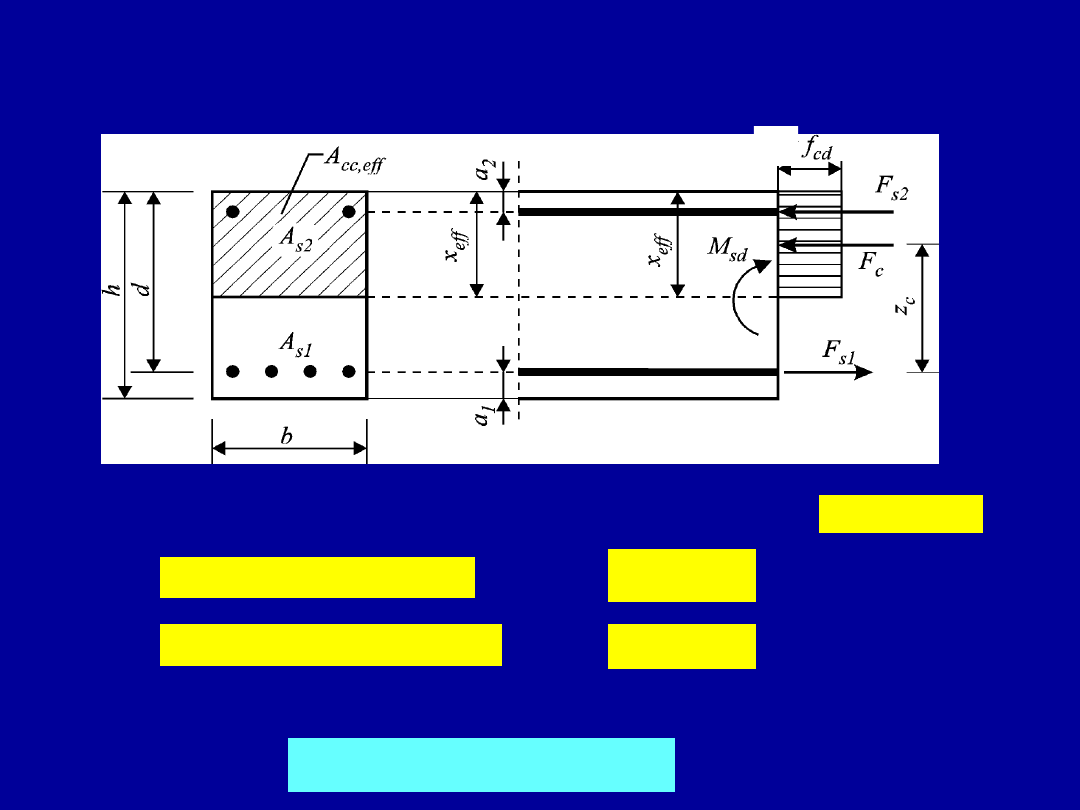
Przekrój prostokątny podwójnie zbrojony

Równanie równowagi sił poziomych na oś podłużną elementu

0

1

2











yd

s

yd

s

cd

ef

f

A

f

A

f

b

x

Równowaga momentów względem osi zbrojenia rozciąganego





2

2

a

d

f

A

z

F

M

M

yd

s

c

c

Rd

Ed









lim

,

ef

ef



 

jeżeli

0

1

2







s

s

c

F

F

F

0

1

2

lim

,











yd

s

yd

s

cd

ef

f

A

f

A

f

b

x

jeżeli

lim

,

ef

ef







30

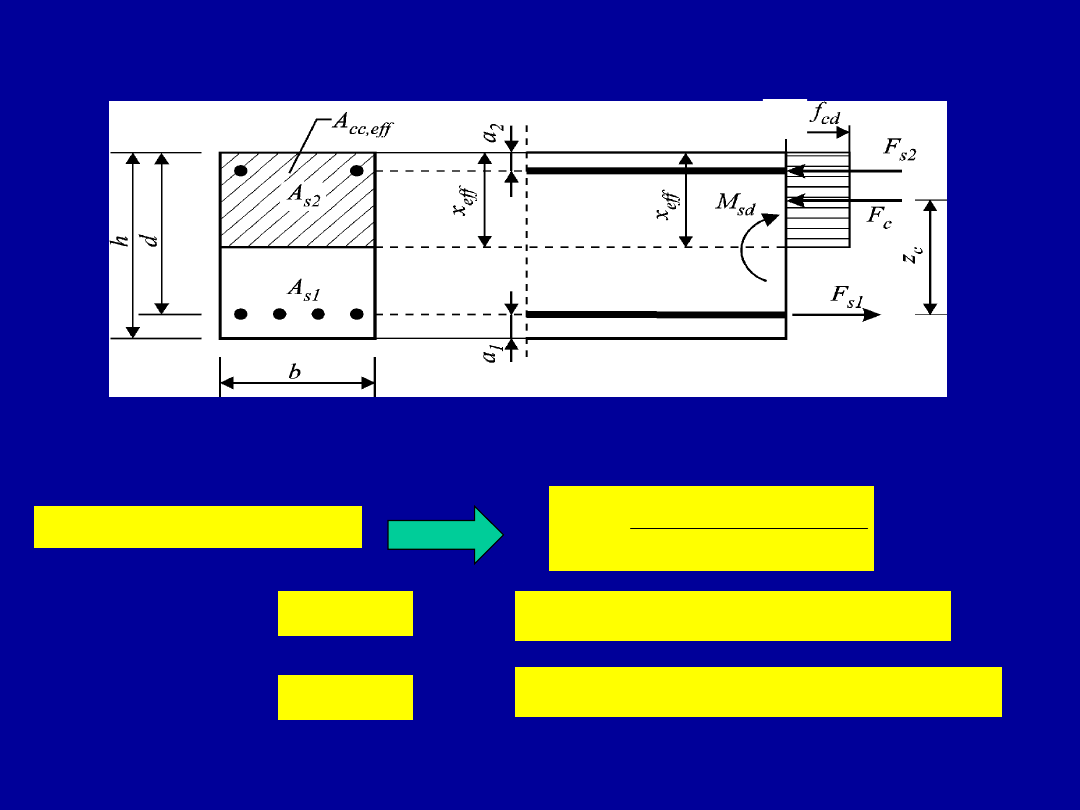
Nośność elementu prostokątnego podwójnie zbrojonego

Z równania równowagi sił poziomych wyznaczamy zasięg strefy ściskanej

0

1

2











yd

s

yd

s

cd

ef

f

A

f

A

f

db



cd

yd

s

yd

s

ef

f

db

f

A

f

A









2

1











2

2

2

5

,

0

1

a

d

f

A

bf

d

M

yd

s

cd

ef

ef

Rd















Jeżeli

lim

,

ef

ef







Jeżeli

lim

,

ef

ef















2

2

2

lim

,

lim

,

5

,

0

1

a

d

f

A

bf

d

M

yd

s

cd

ef

ef

Rd















31

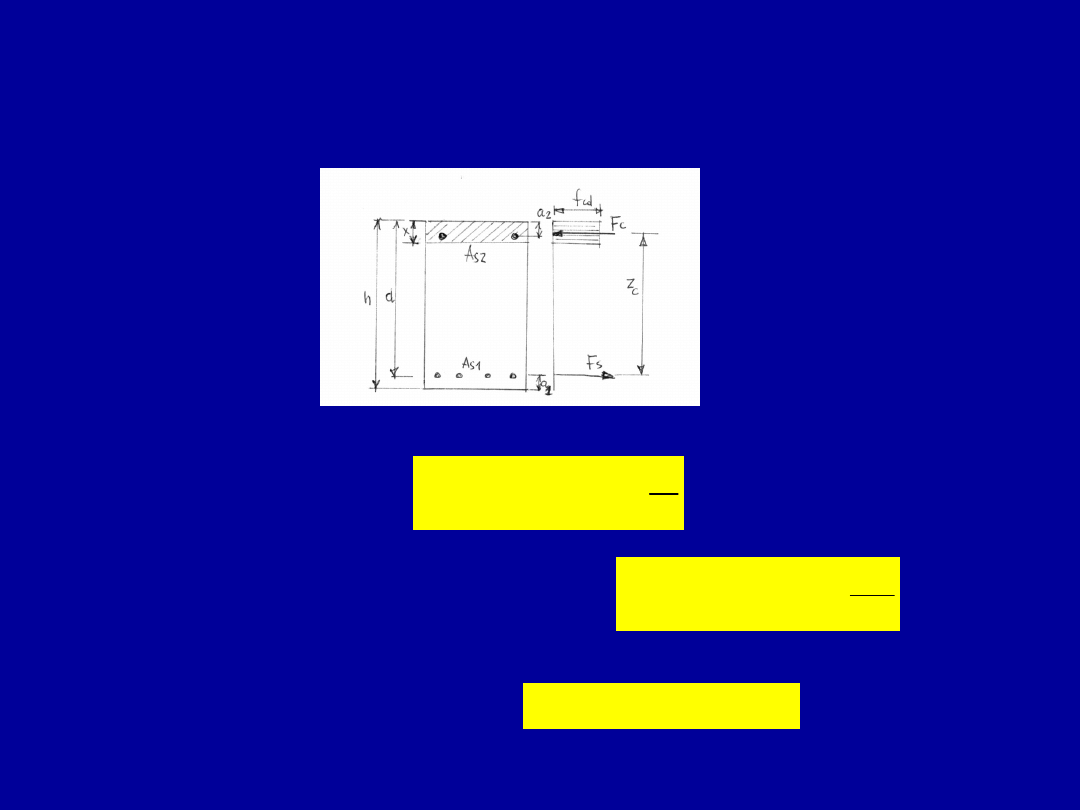
Nośność elementu prostokątnego podwójnie zbrojonego
- przypadek szczególny





2

1

1

a

d

f

A

z

F

M

yd

s

c

s

Rd







Jeżeli

d

a

a

x

ef

ef

2

2

2

czyli

2







Nośność na zginanie wyznacza się zakładając,
że zasięg strefy ściskanej wynosi

d

a

a

x

ef

ef

2

2

2

czyli

2







Zatem nośność na ściskanie wynosi

32

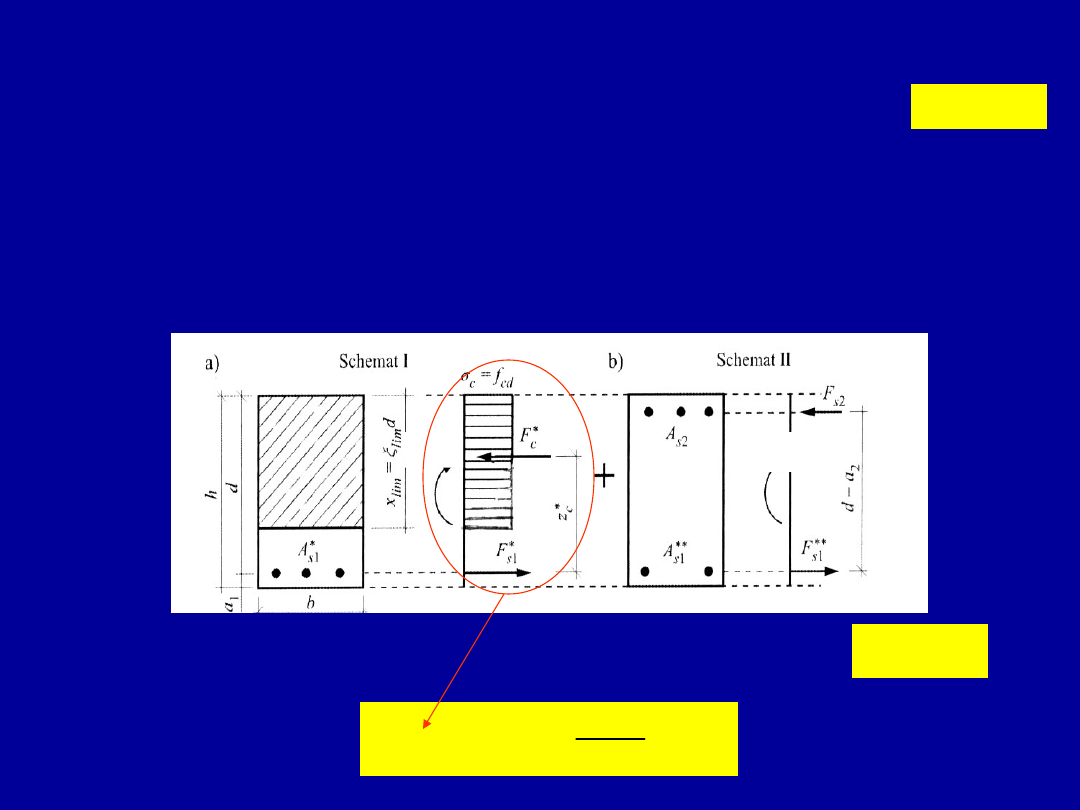
Obliczanie zbrojenia w przekroju

prostokątnym wymagającym

dozbrojenia w strefie ściskanej

Dla zadanych wymiarów b x h przekroju prostokątnego
zginanego momentem o wartości obliczeniowej M

Ed

,

zakładamy klasę betonu i stali zbrojeniowej.

Stosujemy zasadę superpozycji schematów I i II

W schemacie I obliczamy maksymalny moment M

Rd,lim

przyjmując

cd

ef

ef

Rd

f

b

d

M

2

lim

,

lim

,

lim

,

2

1





















lim

,

ef

ef







lim

,

ef

ef







Jeżeli

M

*

Ed

ΔM

Ed

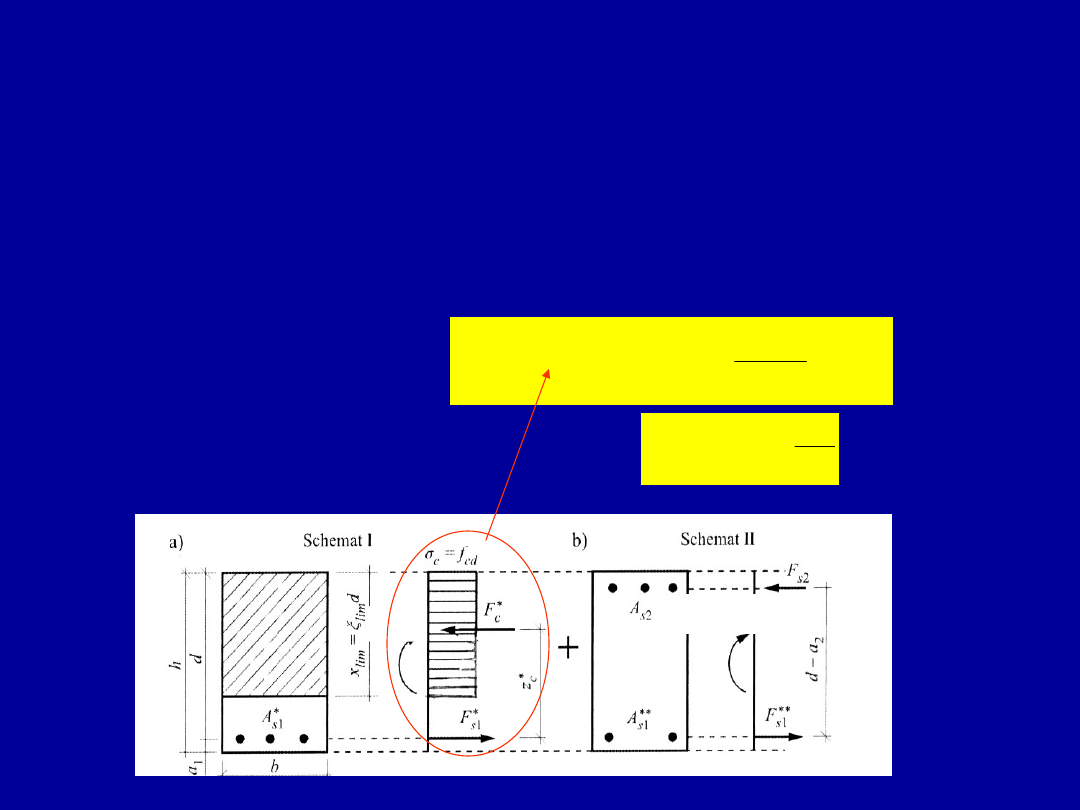
34

Obliczanie zbrojenia w przekroju

prostokątnym wymagającym

dozbrojenia w strefie ściskanej

Stosujemy zasadę superpozycji schematów I i II

cd

ef

ef

Rd

Ed

f

b

d

M

M

2

lim

,

lim

,

lim

,

*

2

1

























yd

cd

ef

s

f

f

db

A

lim

,

*

1





Schemat I

Pole przekroju zbrojenia rozciąganego

Równowaga momentów

M

*

Ed

ΔM

Ed

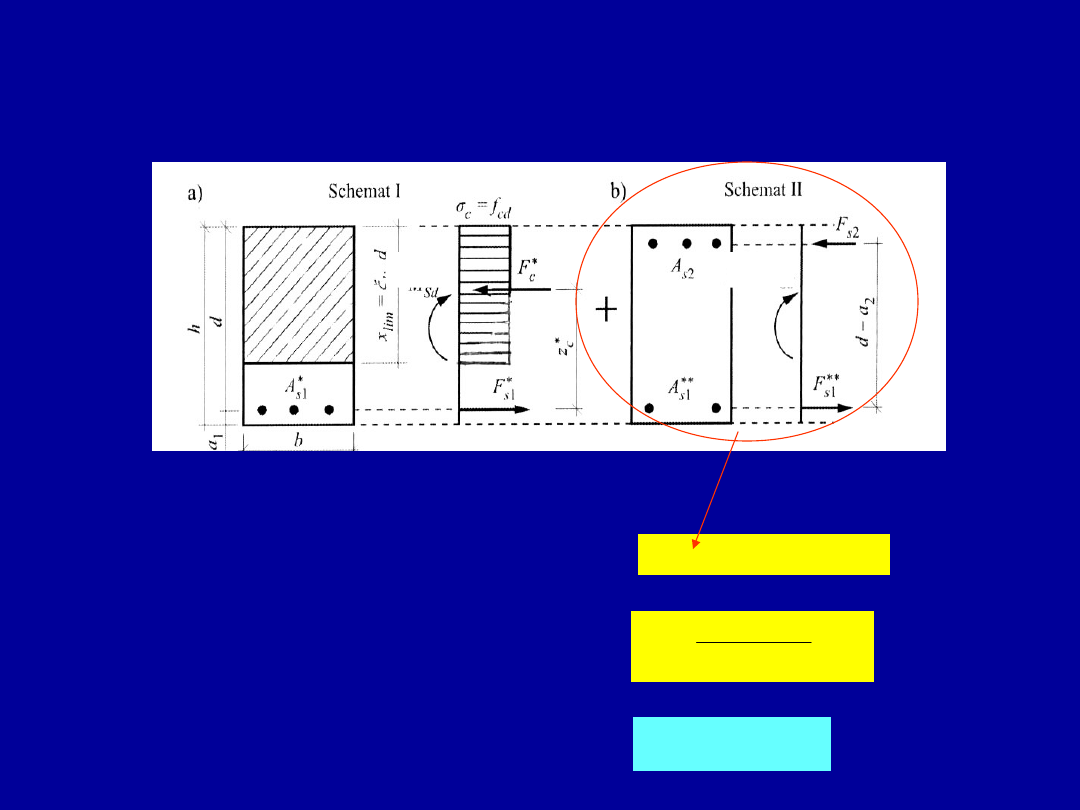
35

Obliczanie zbrojenia w przekroju

prostokątnym wymagającym

dozbrojenia w strefie ściskanej

Schemat II

Nadwyżka momentu sił wewnętrznych

lim

,

Rd

Ed

Ed

M

M

M











*

*

1

2

2

s

yd

Ed

s

A

a

d

f

M

A









Pole przekroju zbrojenia ściskanego
A

s2

równe zbrojeniu rozciąganemu w
schemacie II

Ostatecznie pole zbrojenia wynosi

*

*

1

*

1

1

s

s

s

A

A

A





ΔM

Ed

M

*

Ed

36

Element zginany pojedynczo

zbrojony

o przekroju teowym

37

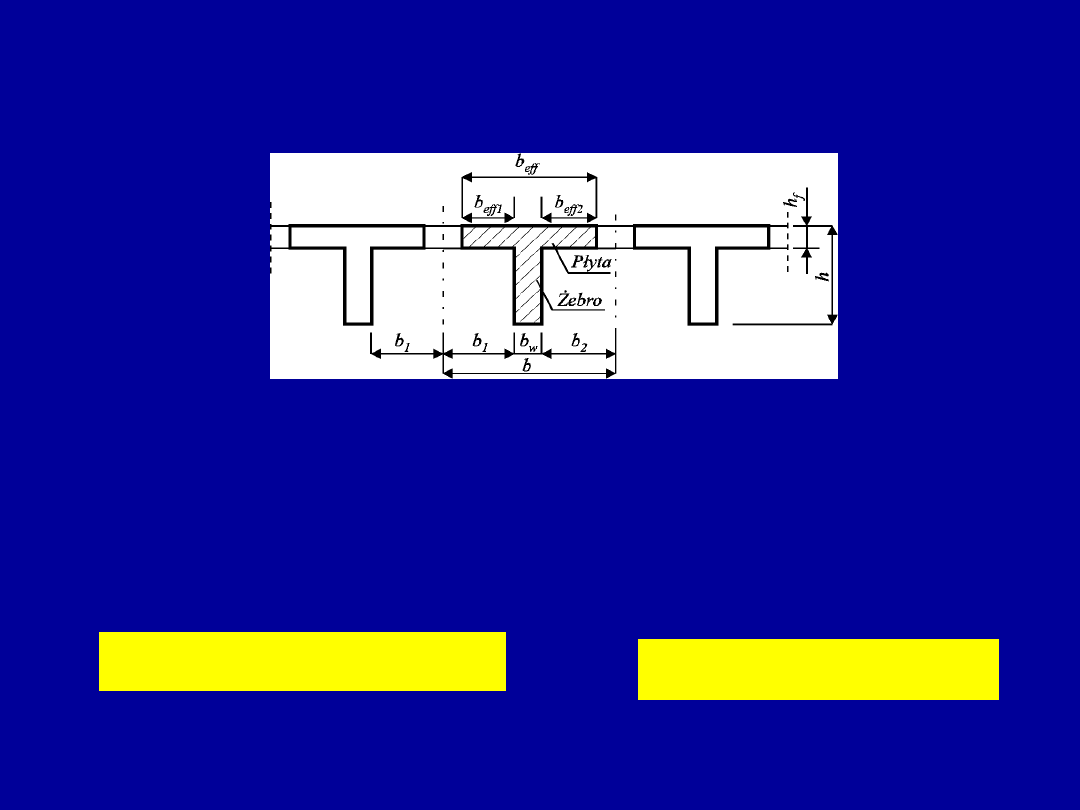
Przekroje zginane o kształcie teowym

Zasady idealizacji
konstrukcji

Efektywną szerokość b

ef

półki w belkach teowych można przyjmować

jako stałą na długości jednego przęsła. Szerokość tę wyznaczać należy

- w belkach teowych przy dwustronnym wysięgu płyty

2

1

,

b

b

b

b

b

b

w

i

ef

w

ef













gdzie l

0

- odległość między punktami wyznaczającymi miejsca zerowych

momentów na długości przęsła elementu.

0

0

,

2

,

0

1

,

0

2

,

0

l

l

b

b

i

i

ef







gdzi
e

38

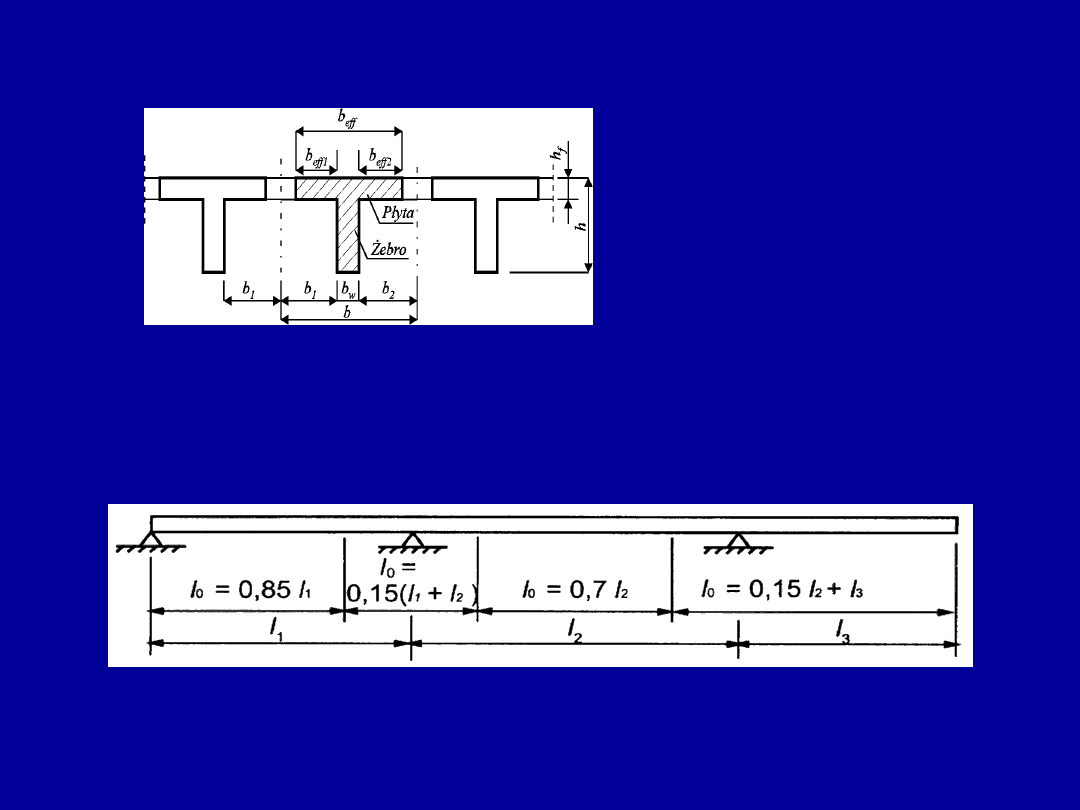
Przekroje o kształcie teowym

Zasady idealizacji
konstrukcji belki
współpracującej z płytą

l

0

- odległość między punktami wyznaczającymi miejsca zerowych

momentów na długości przęsła elementu.

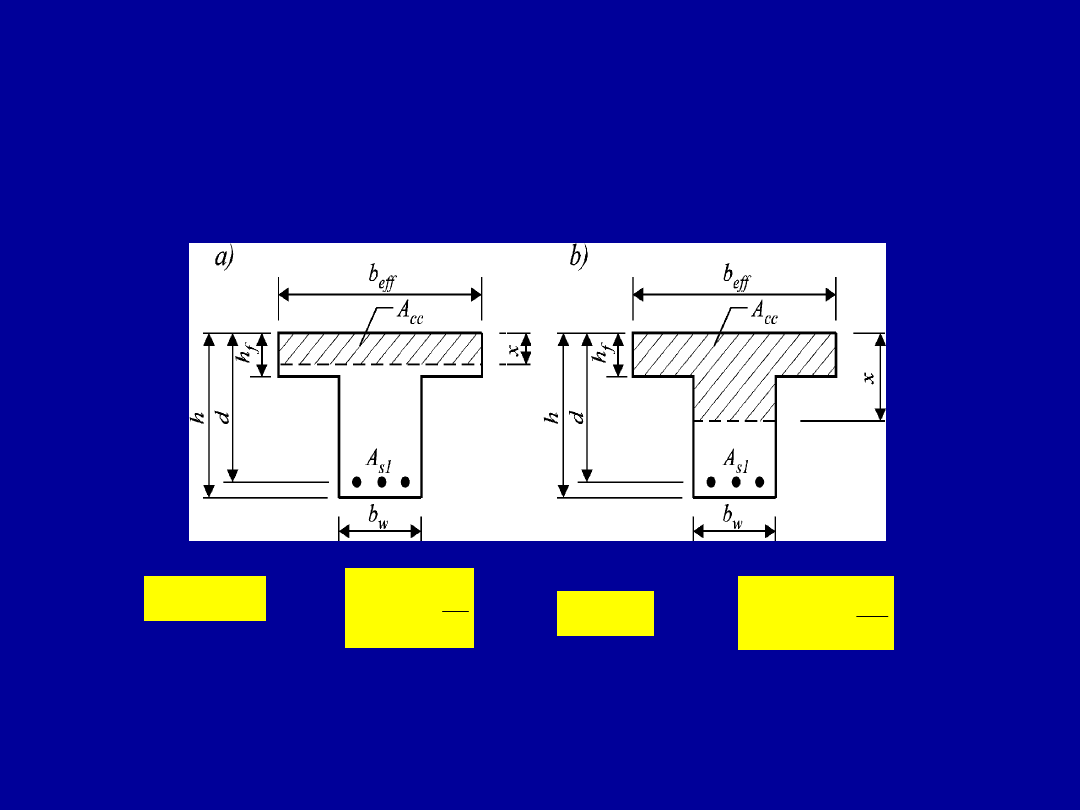
Odcinek l

0

wyznaczający strefę zasięgu naprężeń ściskających

w płycie
współpracującej ze środnikiem zależy od kształtu wykresu
momentów
zginających na elemencie. Długość tę można określić ze
schematu belki ciągłej.

39

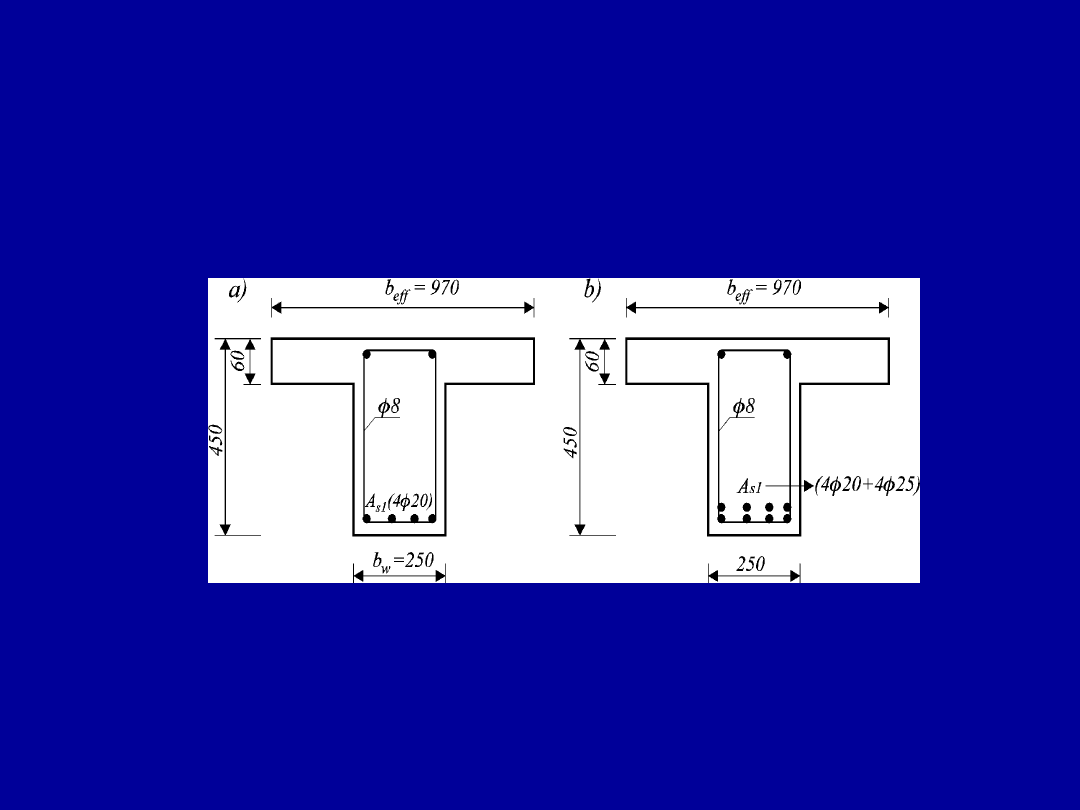
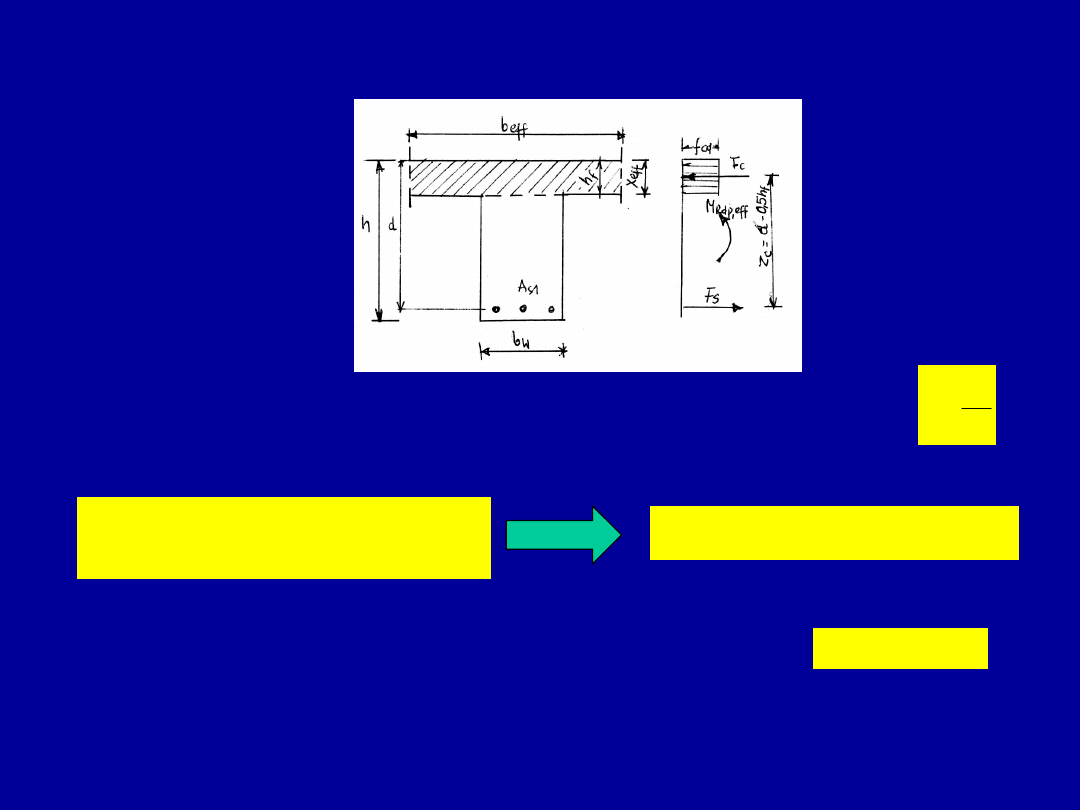
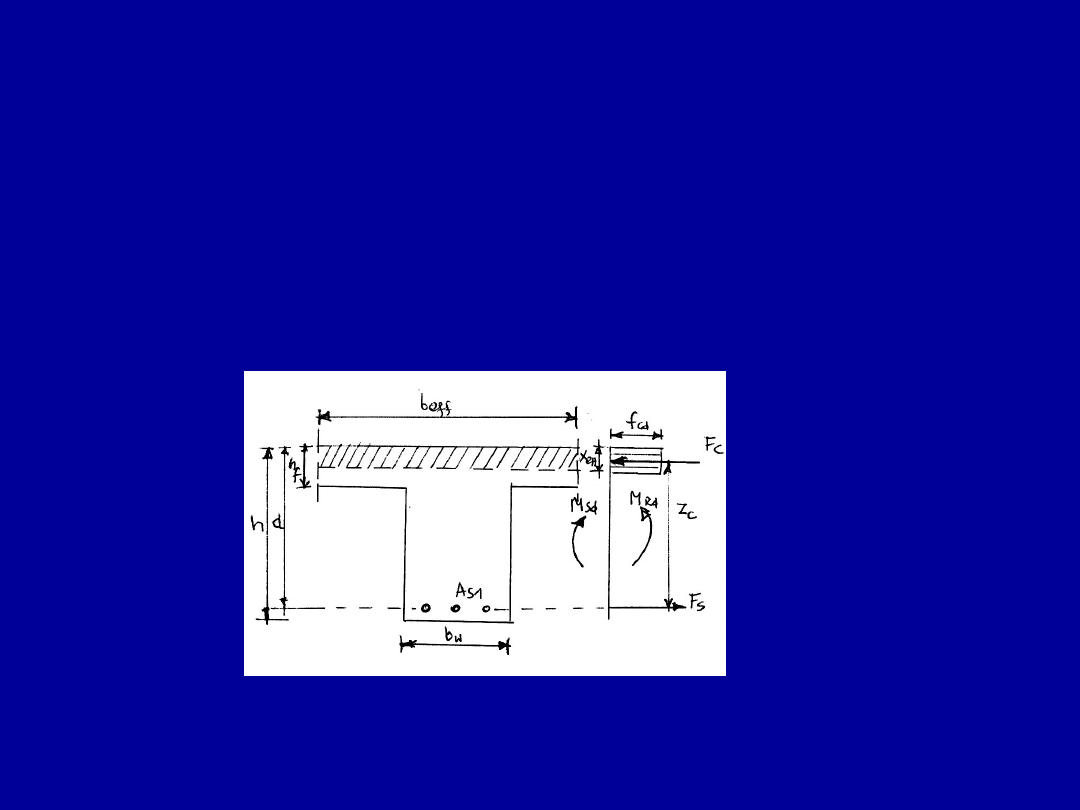
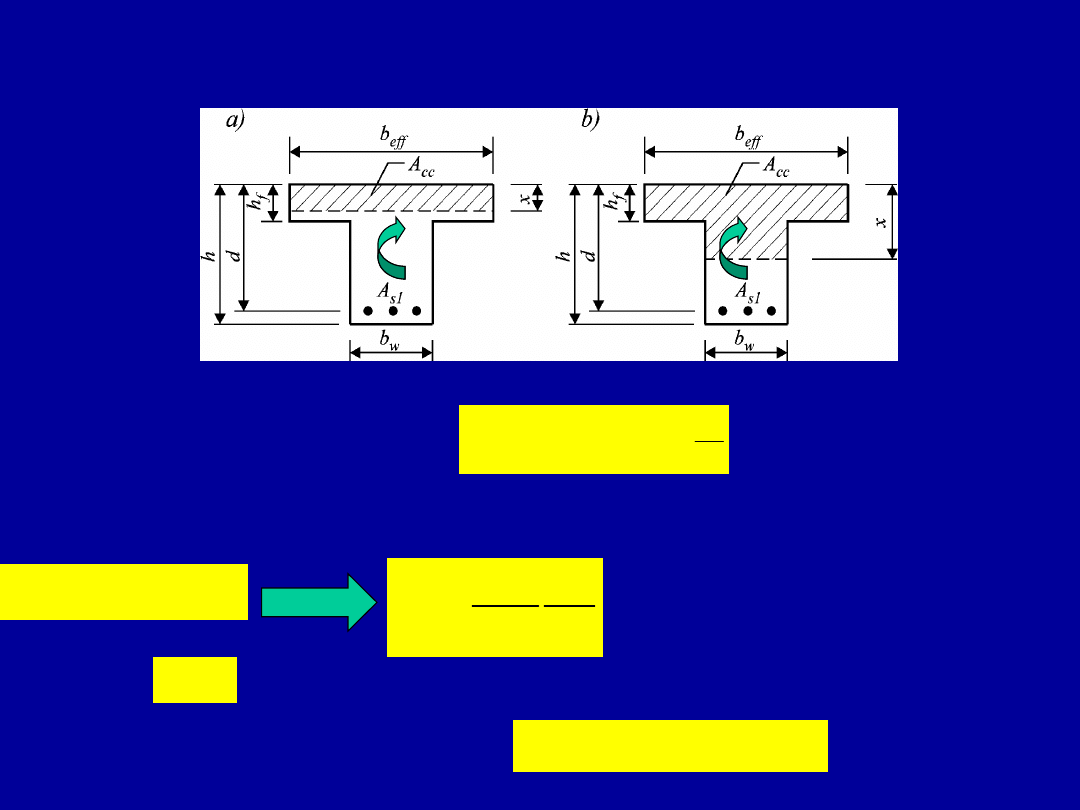
Elementy zginane o przekroju w

kształcie teowym

Dwa przypadki pracy przekroju teowego

a) – przekrój pozornie teowy, b) – przekrój rzeczywiście teowy

f

ef

h

x 

lub

d

h

f

ef









f

ef

h

x 

d

h

f

ef









lub

40

Ustalenie przypadku pracy belki o

przekroju teowym

Określa się moment graniczny M

Rdp,ef

,

obliczony względem

osi zbrojenia rozciąganego przy



ef

=



.





cd

ef

ef

Rdp

f

b

d

M

2

,

5

,

0

1



 



Przekrój jest pozornie teowy, jeżeli spełniony jest warunek

ef

Rdp

Ed

M

M

,



W przeciwnym przypadku występuje przekrój
rzeczywiście teowy.





 

 



 

 



c

c

z

f

F

cd

f

ef

c

c

ef

Rdp

h

d

f

h

b

z

F

M

5

,

0

,











d

h

f





41

 Obliczanie zbrojenia przekroju

pozornie teowego pojedynczo

zbrojonego

W przypadku przekroju pozornie teowego zadanie
sprowadza się
do obliczenia zbrojenia w przekroju o kształcie
prostokątnym
polu powierzchni strefy ściskanej A

cc,ef

= x

ef

b

ef

.

Wymiarowanie rozpoczynamy od obliczenia współczynnika pomocniczego



2

d

b

f

M

ef

cd

Ed

ef







Pole przekroju zbrojenia rozciąganego można obliczyć na dwa sposoby:

yd

cd

ef

ef

s

f

f

db

A







1

lub





yd

ef

Ed

s

f

d

M

A



5

,

0

1

1





Zadanie sprowadza się do obliczenia zbrojenia w
przekroju o kształcie prostokątnym o polu powierzchni
strefy ściskanej A

cc,ef

= x

ef

b

ef

.

ef

ef

ef

ef

















0

2

2

2

lim

,

2

1

1

ef

ef

ef

















Obliczanie zbrojenia przekroju pozornie

teowego pojedynczo zbrojonego

43

 Obliczanie zbrojenia przekroju

pozornie teowego pojedynczo

zbrojonego

Można też wykorzystać tablice. Należy obliczyć współczynnik do tablicy



ef

,

ef

ef

ef

cd

Ed

ef

d

b

f

M







,

2







Pole przekroju zbrojenia rozciąganego można obliczyć na dwa sposoby:

yd

cd

ef

ef

s

f

f

db

A







1

lub

yd

ef

sd

s

f

d

M

A





1

ef

lub





ef

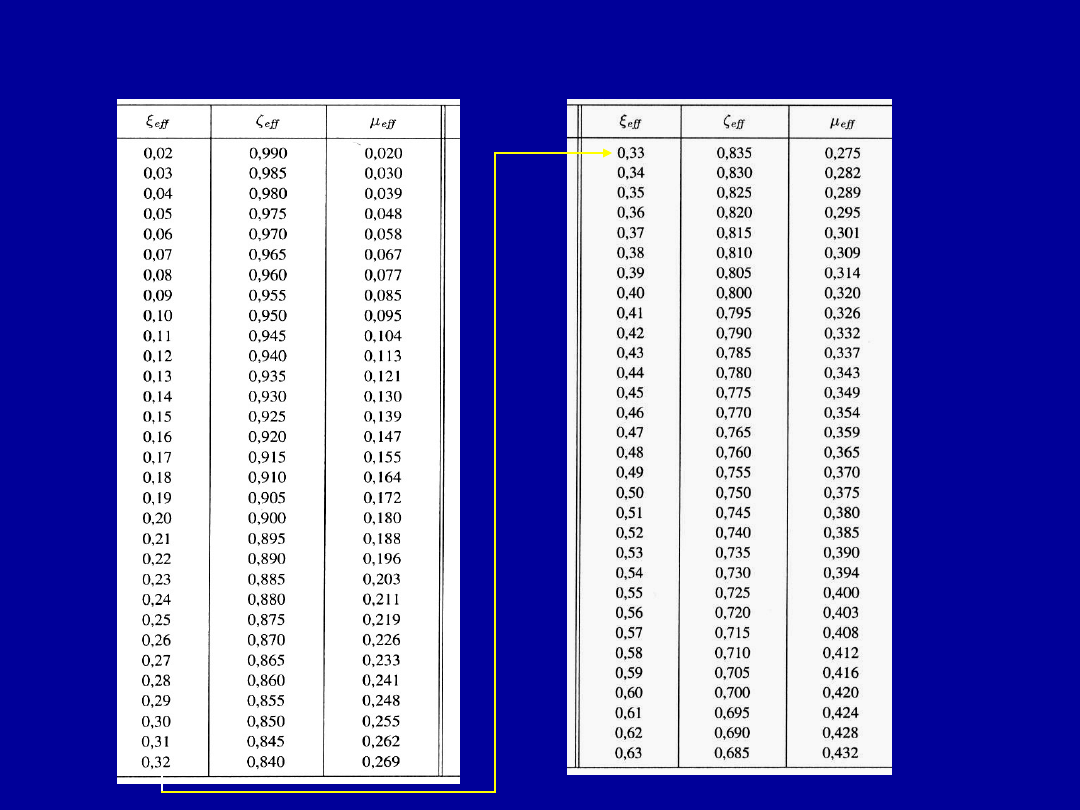
44

Tablice współczynników do projektowania elementu zginanego o przekroju prostokątnym

metodą uproszczoną

45

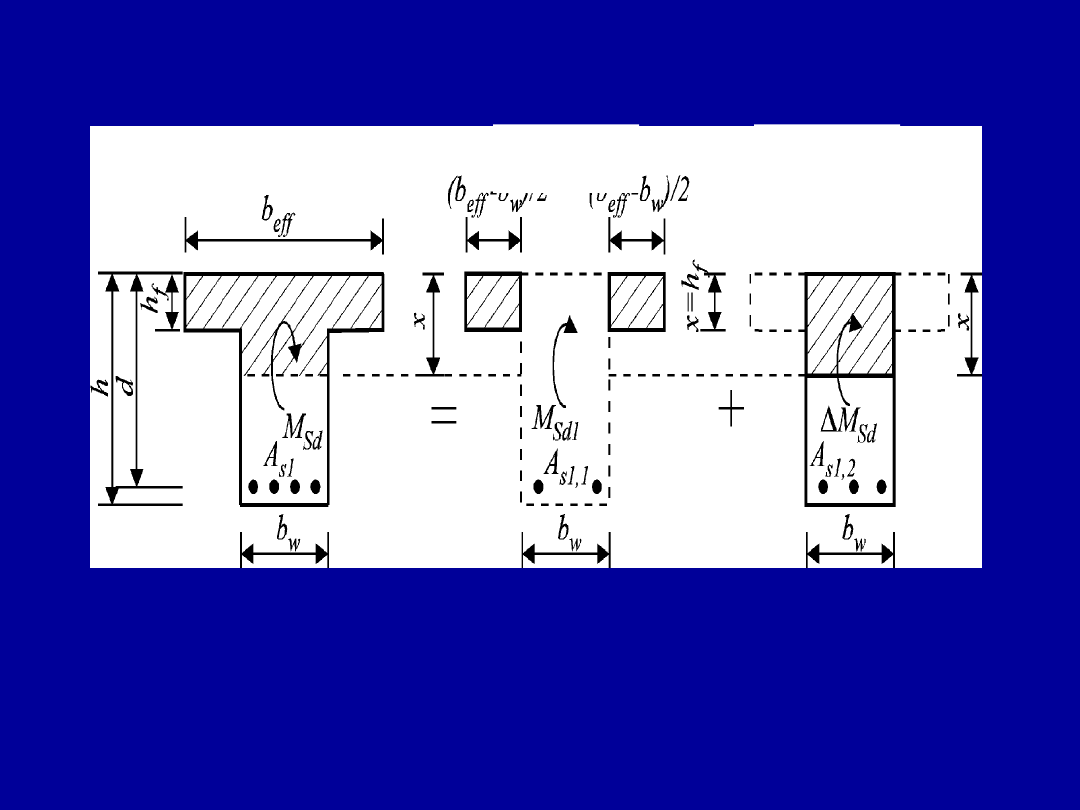
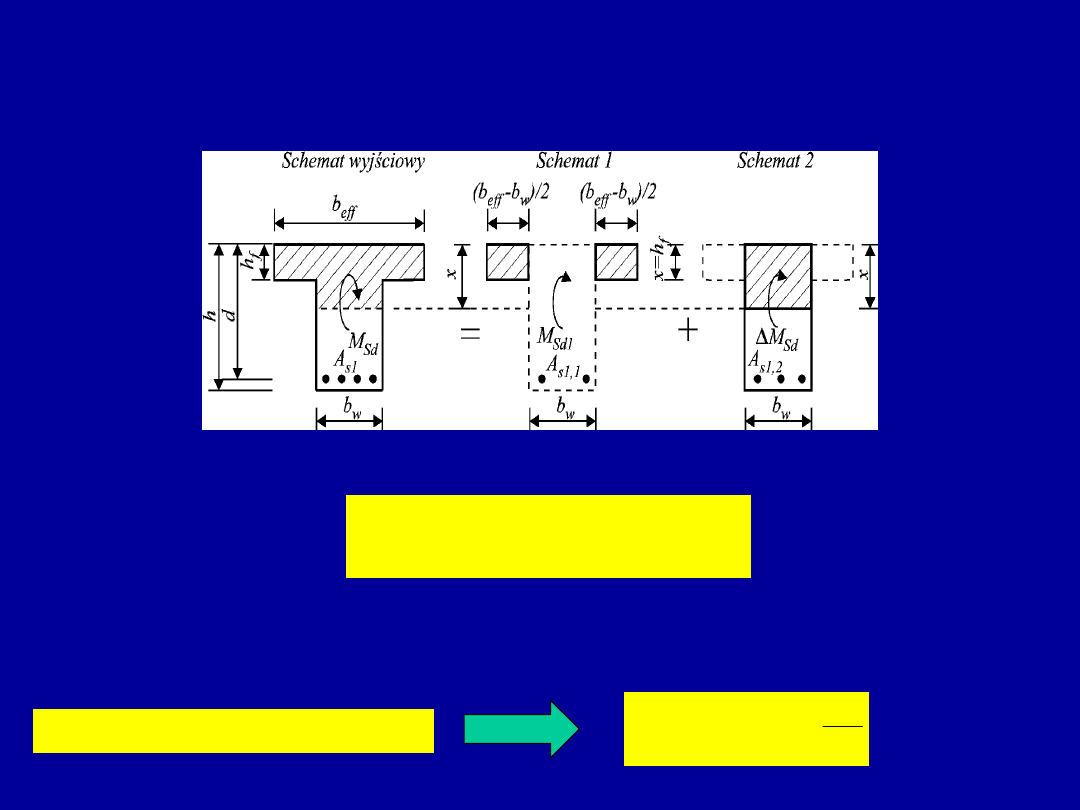
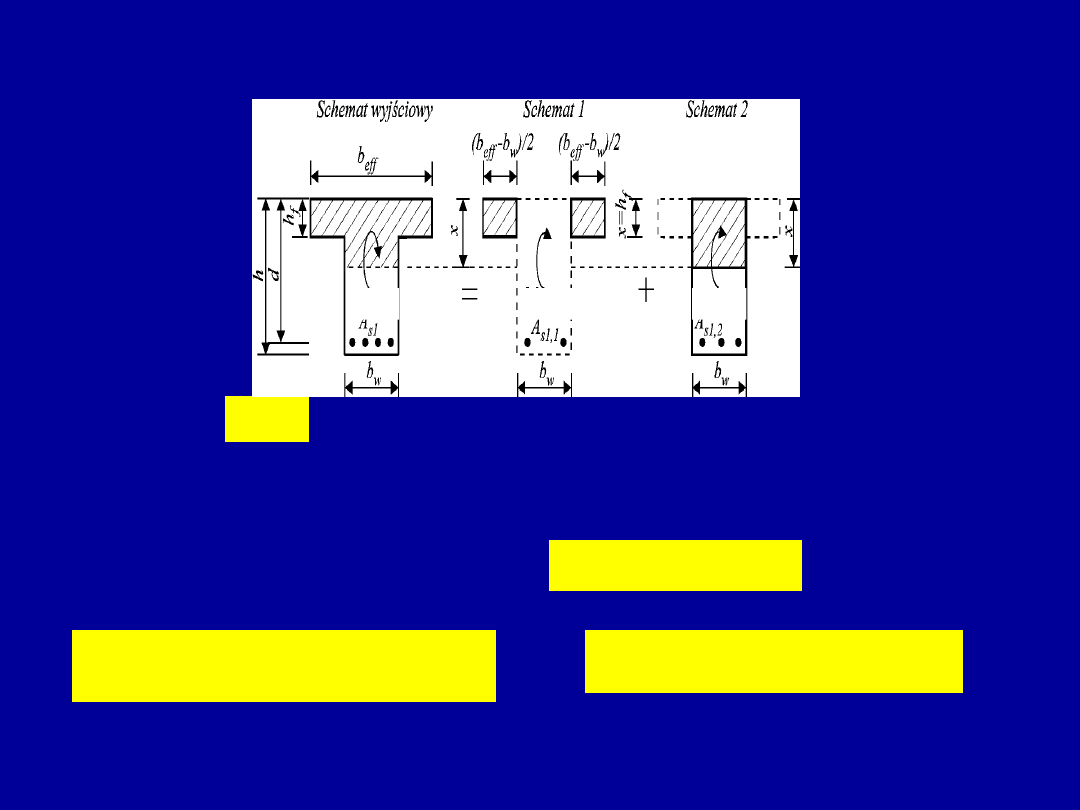
Schemat
wyjściowy

Schemat
1

Schemat
2

 Obliczanie zbrojenia przekroju rzeczywiście teowego

Stosuje się zasadę superpozycji schematów 1 i 2

46

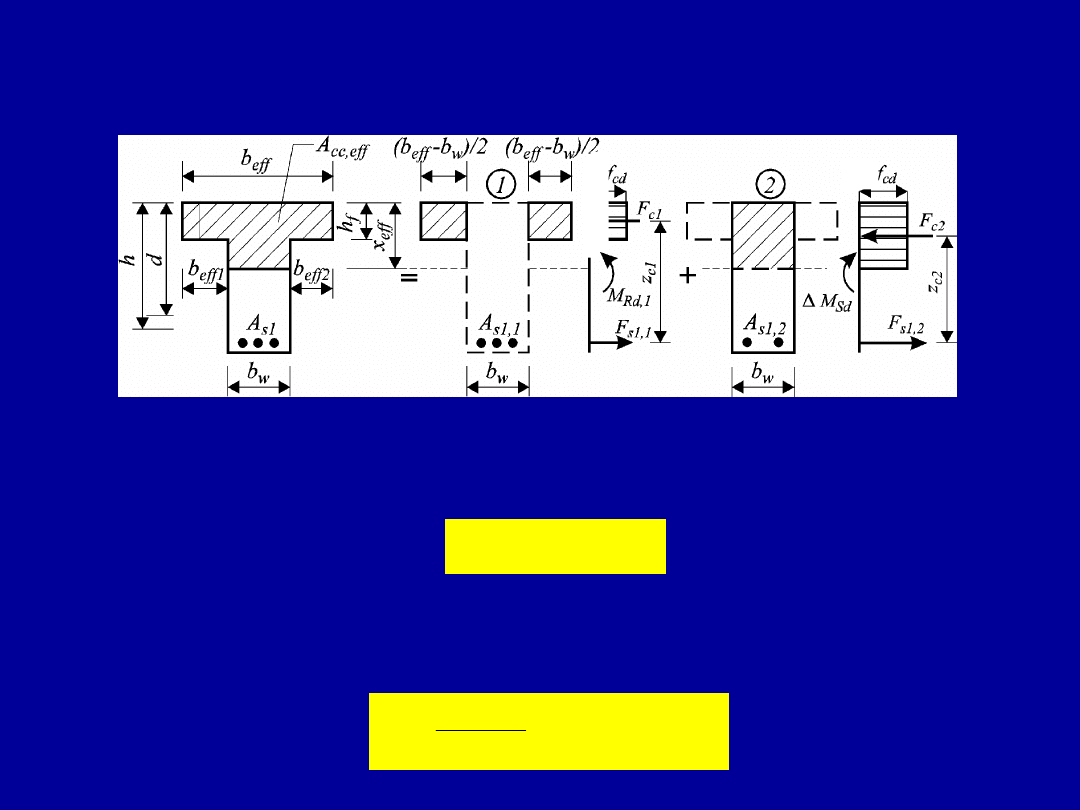
Nośność graniczną przekroju w schemacie „1” zapisujemy



 



 

 





















1

1

5

,

0

1

,

c

c

z

f

F

cd

w

ef

f

Rd

h

d

f

b

b

h

M







Zbrojenie A

s1

w schemacie „1” obliczamy z równania sumy rzutów wypadkowych

sił F

c1

i F

s1,1

na oś podłużną belki.





yd

cd

w

ef

f

s

f

f

b

b

h

A





1

,

1

 Obliczanie zbrojenia przekroju

rzeczywiście teowego





cd

f

w

ef

yd

s

c

s

f

h

b

b

f

A

F

F









1

,

1

1

1

,

1

47

W schemacie „2” przekrój teowy jest obciążony różnicą momentów – zewnętrznego
i odpowiadającego nośności przekroju w schemacie „1”

1

,

Rd

Ed

M

M

M







Na podstawie współczynnika wejściowego



ef

znajdujemy efektywny zasięg

strefy ściskanej



ef

oraz współczynnik pomocniczy



ef

ef

ef

tablicy

z

cd

w

ef

f

d

b

M







,

2















Schemat 2

48

Przekrój rzeczywiście teowy oblicza się jako pojedynczo zbrojony, jeżeli

lim

,

ef

ef







yd

cd

w

ef

s

f

f

db

A





2

,

1

Pole przekroju zbrojenia w schemacie 2 obliczymy
jak dla przekroju prostokątnego o szerokości b

w

yd

ef

Ed

s

df

M

A





2

,

1

lub

2

,

1

1

,

1

1

s

s

s

A

A

A





Ostatecznie pole zbrojenia rozciąganego otrzymujemy

Przekrój oblicza się jako podwójnie zbrojony, jeżeli

lim

,

ef

ef







49

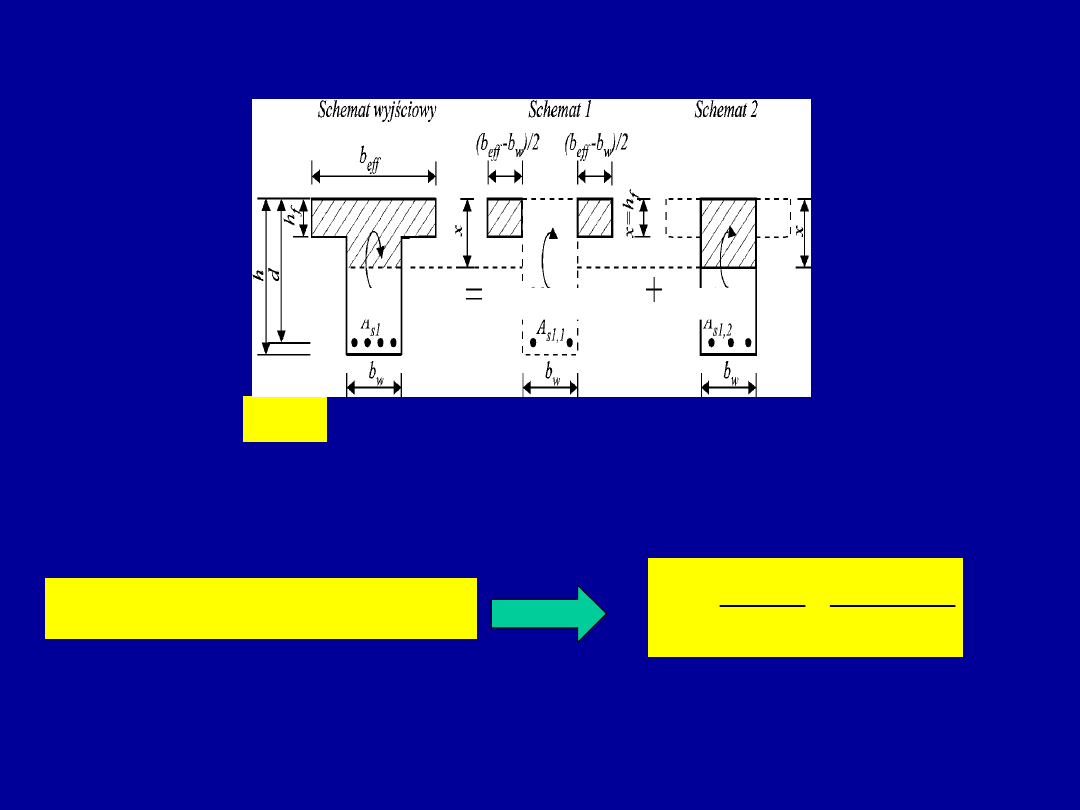
Wstępnie można założyć, że
przekrój jest pozornie teowy

d

h

h

x

f

ef

f

ef











czyli

Na podstawie równania równowagi sił podłużnych otrzymamy zasięg
strefy ściskanej

yd

s

cd

ef

ef

f

A

f

db

1





Wyznaczanie nośności przekroju teowego M

Rd

cd

yd

ef

s

ef

f

f

d

b

A

1





to nośność strefy ściskanej
wynosi





cd

ef

ef

ef

Rd

f

b

d

M

2

5

,

0

1









Jeżel
i







ef

M

Rd

= ?

M

Rd

= ?

50

Oznacza to, że założenie było błędne
i przekrój
jest rzeczywiście teowy

Zasięg strefy ściskanej trzeba wyznaczyć
ponownie





0

1









yd

s

cd

ef

cd

w

ef

f

A

df

f

b

b

d





Określanie nośności przekroju teowego





w

w

ef

cd

ef

yd

s

ef

b

b

b

df

b

f

A











1

Jeżel
i







ef

M

Rd

M

Rd1d

M

Rd2

51

to przekrój jest rzeczywiście teowy

Po wyznaczeniu zasięgu strefy ściskanej
suma nośności obu schematów wynosi

Określanie nośności przekroju teowego

Jeżel
i







ef

M

Rd

M

Rd1d

M

Rd2

2

1

Rd

Rd

Rd

M

M

M













cd

w

ef

Rd

f

d

b

b

M

2

1

5

,

0

1















cd

w

ef

ef

Rd

f

d

b

M

2

2

5

,

0

1









52

Koniec wykładu 3