1

Obliczenia elementów

żelbetowych

na skręcanie i docisk

WYKŁAD Nr 8

PODSTAWY

PROJEKTOWANIA

KONSTRUKCJI

ŻELBETOWYCH

Semestr V , r .ak. 2010/2011

Opracowanie - prof. dr hab. inż. Andrzej Łapko

2

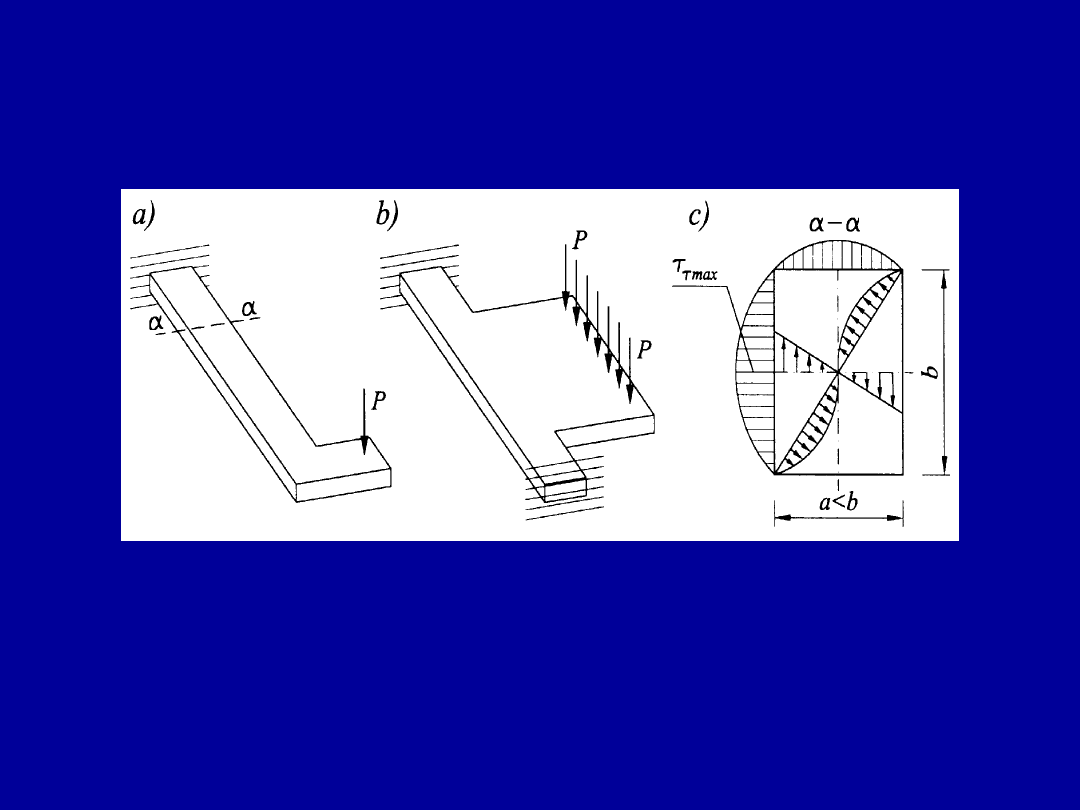
Elementy skręcane

W konstrukcjach budowlanych naprężenia od skręcania z reguły występują

w połączeniu z naprężeniami normalnymi pochodzącymi od zginania.

3

Wskutek działania momentu skręcającego T powstają

naprężenia ścinające



T

w przekrojach elementów. Rozkład

naprężeń zależy od kształtu przekroju, a także od

kierunku i usytuowania linii przekrojowej.

Według teorii sprężystości maksymalne naprężenia ścinające
przy skręcaniu swobodnym określamy jako:

- w prętach o przekroju kolistym o promieniu r

T

T

J

r

T 



max



r

T

E

d

4

Rozkład naprężeń ścinających wywołanych
działaniem momentu skręcającego wzdłuż
wybranych krawędzi prostokątnego przekroju

Określanie maksymalnych naprężeń

ścinających

przy czystym skręcaniu

- w prętach o przekroju prostokątnym i wymiarach boków a i b (a  b)

b

a

T

T

2

max







b

a

J

T

3





gdzie:

,  - współczynniki określone na podstawie analogii błonowej Prandtla

a

b







45

,

0

6

,

2

3

1



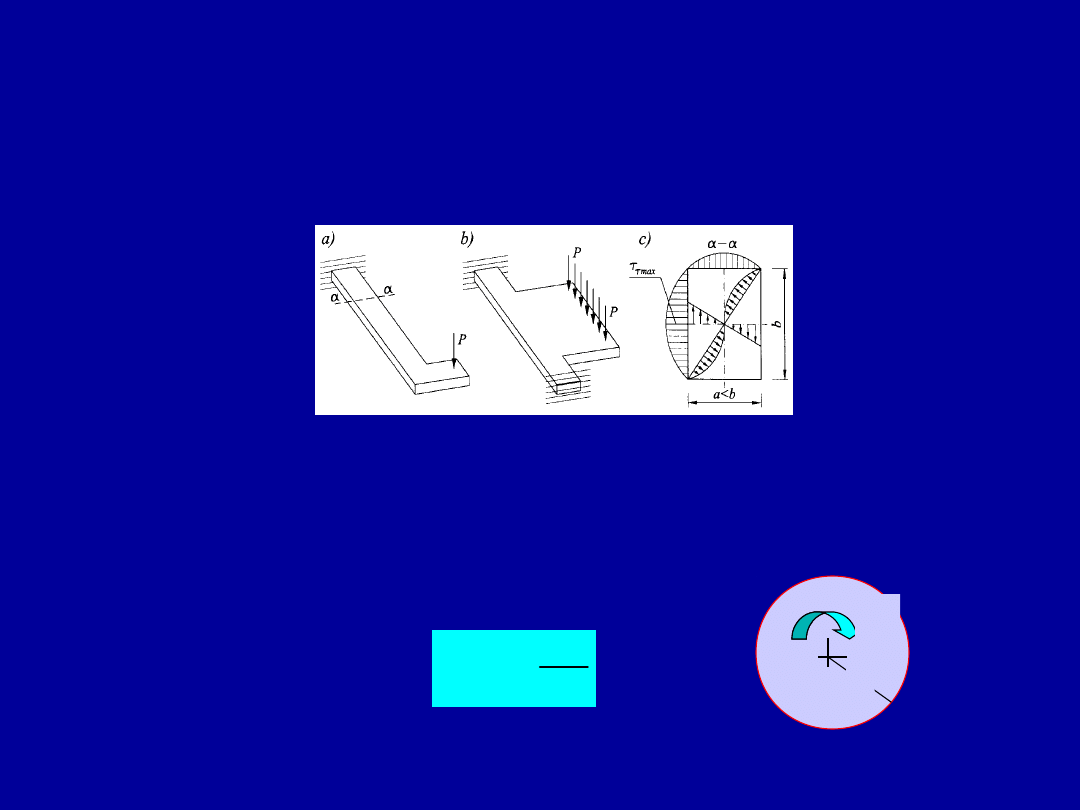
5

W skręcanych prętach cienkościennych o przekroju poprzecznym
złożonym z n przekrojów prostokątnych (rys a) naprężenia ścinające
od skręcania można obliczać ze wzoru







n

i

i

i

T

b

a

T

1

2

max

3



gdzie wyrażenie

oblicza się w każdym z prostokątów o bokach a i b (przy a << b)

3

2

b

a

6

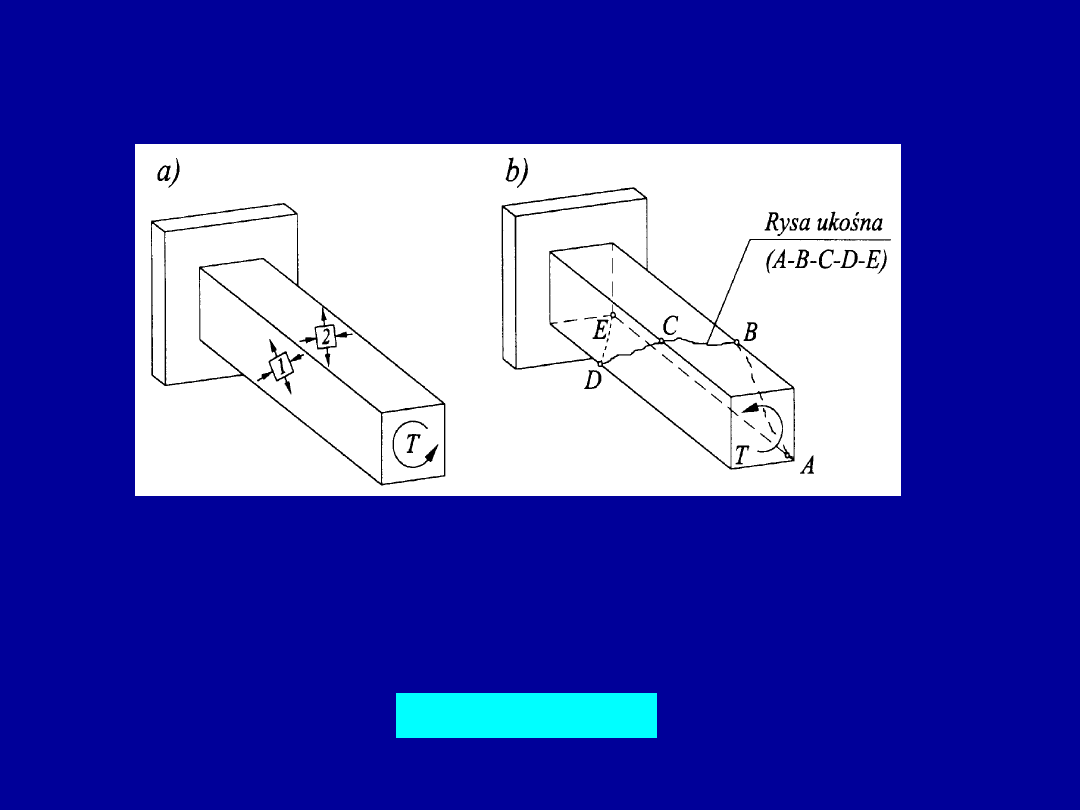
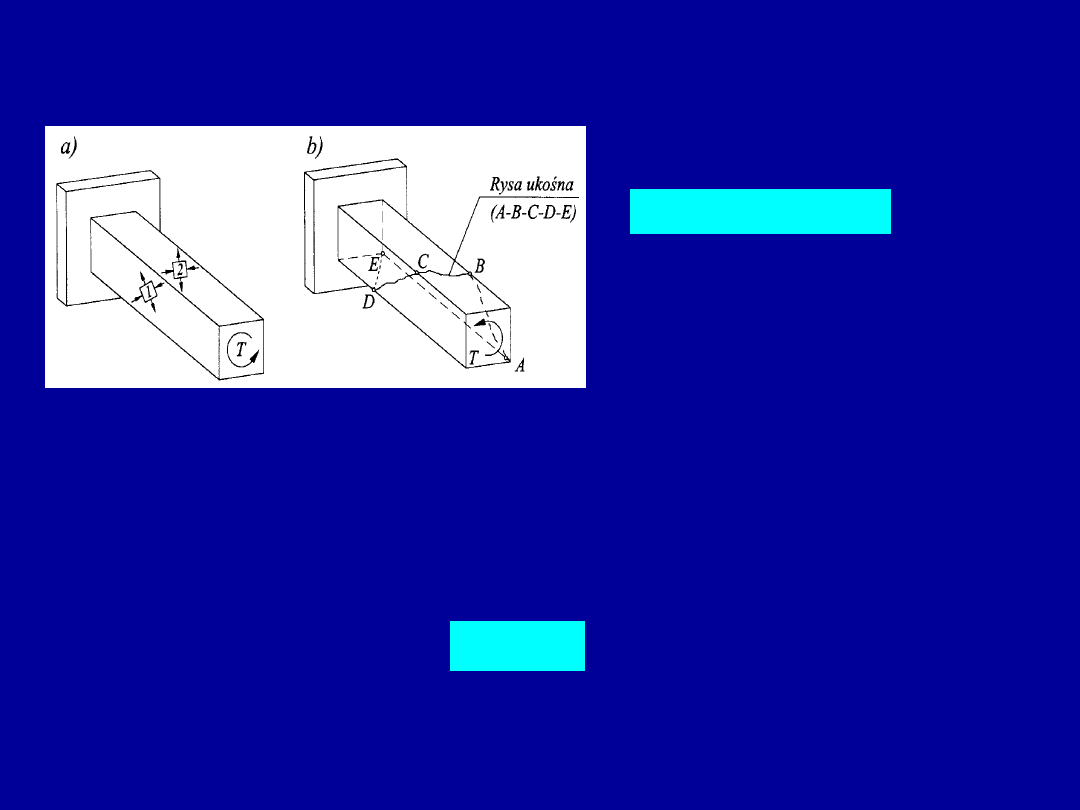
Naprężenia główne i rysy ukośne

w żelbetowych elementach skręcanych

W wyniku skręcania pręta pryzmatycznego powstają naprężenia ścinające
na wszystkich powierzchniach bocznych. Naprężenia główne w przekroju
są równe ścinającym tylko wtedy, gdy ustrój jest obciążony wyłącznie
momentem skręcającym. W tym przypadku otrzymujemy

max

2

1

T













7

Naprężenia główne w elementach skręcanych i ich efekty

w postaci rys ukośnych

max

2

1

T













Trajektoria naprężenia rozciągającego



1

jest nachylona pod kątem

 = 45

o

do krawędzi elementu. Naprężenie to może wywołać rysy ukośne okalające
powierzchnie boczne elementu.

Jeżeli na element jednocześnie działają moment skręcający i siła poprzeczna,
do obliczeń stosujemy zasadę superpozycji

s

T











1

gdzie:



T

- naprężenie ścinające wywołane skręcaniem,



s

- naprężenie ścinające wywołane siłą poprzeczną

8

Wymiarowanie elementów żelbetowych na skręcanie

wg PN-EN 1992-1-1:2008

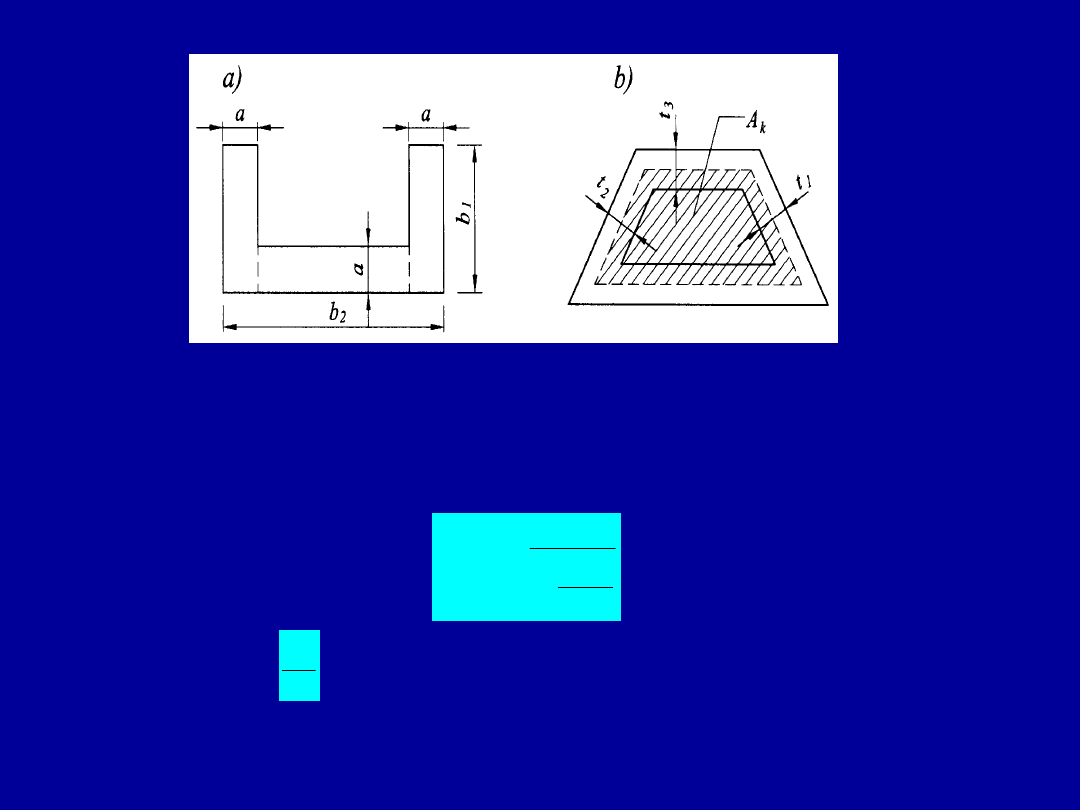
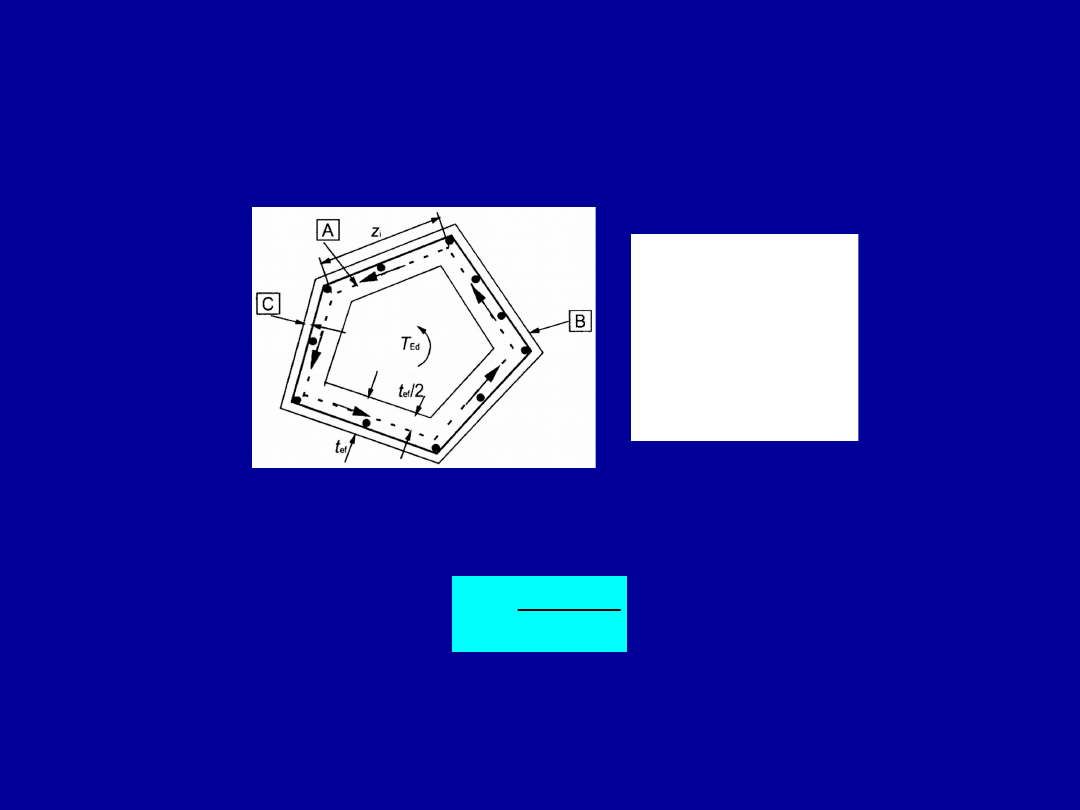
W teorii tej przekroje żelbetowe (pełne lub skrzynkowe) rozpatruje się

jako wydrążone przekroje cienkościenne

Naprężenia ścinające od skręcania w zamkniętym przekroju cienkościennym

zapisuje się zgodnie ze wzorem de Bredta

ef

k

Ed

t

t

A

T

2





gdzie: t

ef

– ekwiwalentna grubość ścianki, w której oblicza się naprężenia,

A

k

– pole powierzchni całego przekroju ograniczone linią poprowadzoną

w środku ciężkości ścianek (obwód wynosi u

k

)

A - linia środkowa

B – zewnętrzna krawędź

przekroju efektywnego,

obwód u,

C - otulina

9

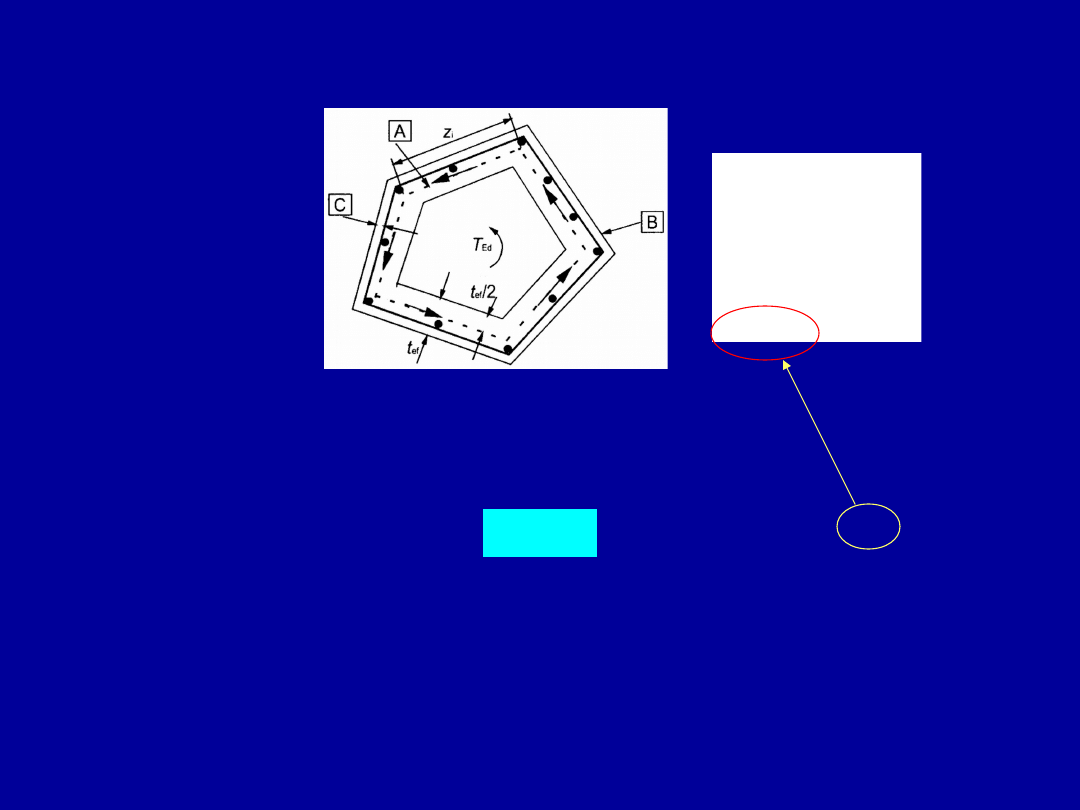
Wymiarowanie elementów żelbetowych na skręcanie

gdzie: t

ef,i

– efektywna grubość ścianki, dla której oblicza się naprężenia,

A – pole powierzchni całego przekroju ograniczone linią poprowadzoną

na obwodzie przekroju u

W przekrojach pełnych należy wyodrębnić ekwiwalentną „grubość” ścianki.
Grubość tę można zapisać

u

A

t

i

ef

/

,



A - linia środkowa

B – zewnętrzna krawędź

przekroju efektywnego,

obwód u,

C - otulina

lecz nie mniej niż 2c

10

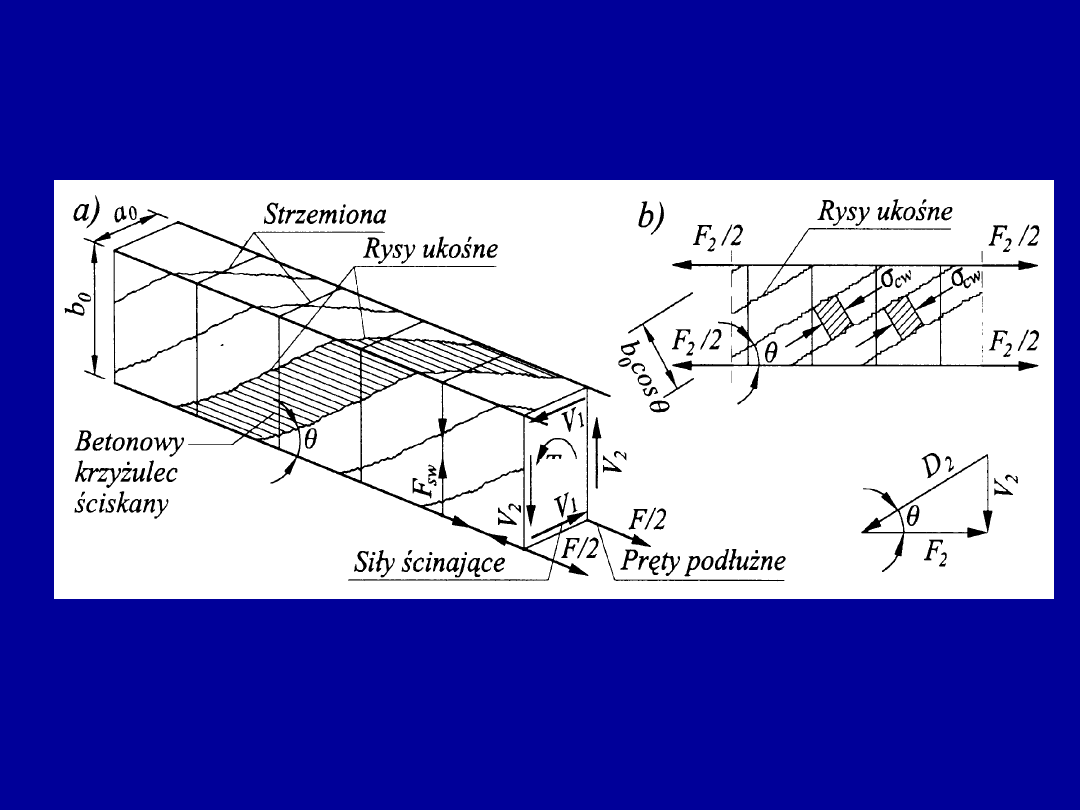
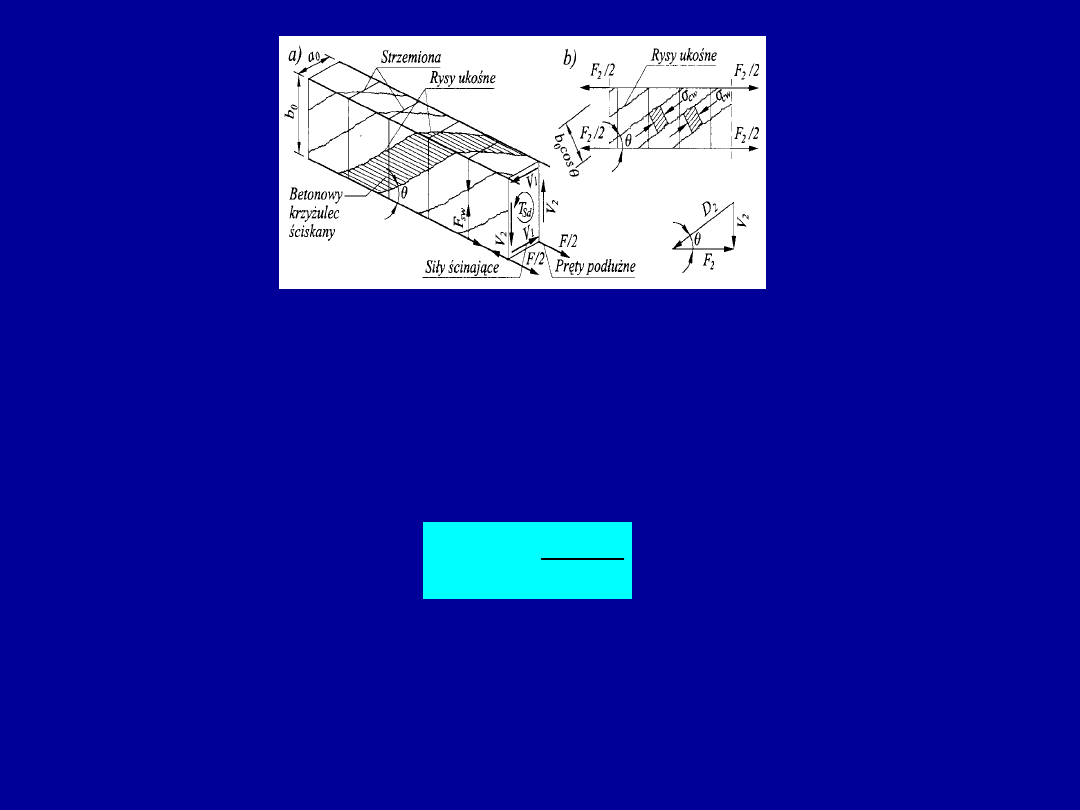
Obliczeniowy model kratownicy przestrzennej

w obliczeniach elementów skręcanych wg PN-EN 1992-

1-1:2008

W rozpatrywanym modelu element jest zastępowany ustrojem złożonym z:

- podłużnych prętów zbrojenia głównego (umieszczonego w narożach przekroju),
- zamkniętych rozciąganych strzemion (prostopadłych lub ukośnych),
- ściskanych krzyżulców betonowych nachylonych pod kątem

 do osi elementu.

T

Ed

11

Przekrój poprzeczny kratownicy (ustalony między środkami ciężkości prętów podłużnych)
ma wymiary a

0

x b

0

(odpowiada polu powierzchni rdzenia przekroju).

Kąt nachylenia

 krzyżulców ściskanych nie może przekroczyć

45

o

.

Na podstawie wzoru de Bredta dla zamkniętego przekroju cienkościennego otrzymujemy
wzór na strumień siły ścinającej

k

Ed

ef

A

T

t







2



gdzie:

 • t

ef

- strumień siły ścinającej na jednostkę długości obwodu rdzenia,

A

k

- powierzchnia rdzenia zawartego wewnątrz linii środkowej (w przekrojach

skrzynkowych A

k

oblicza się łącznie z powierzchnią wewnętrznej części pustej).

12

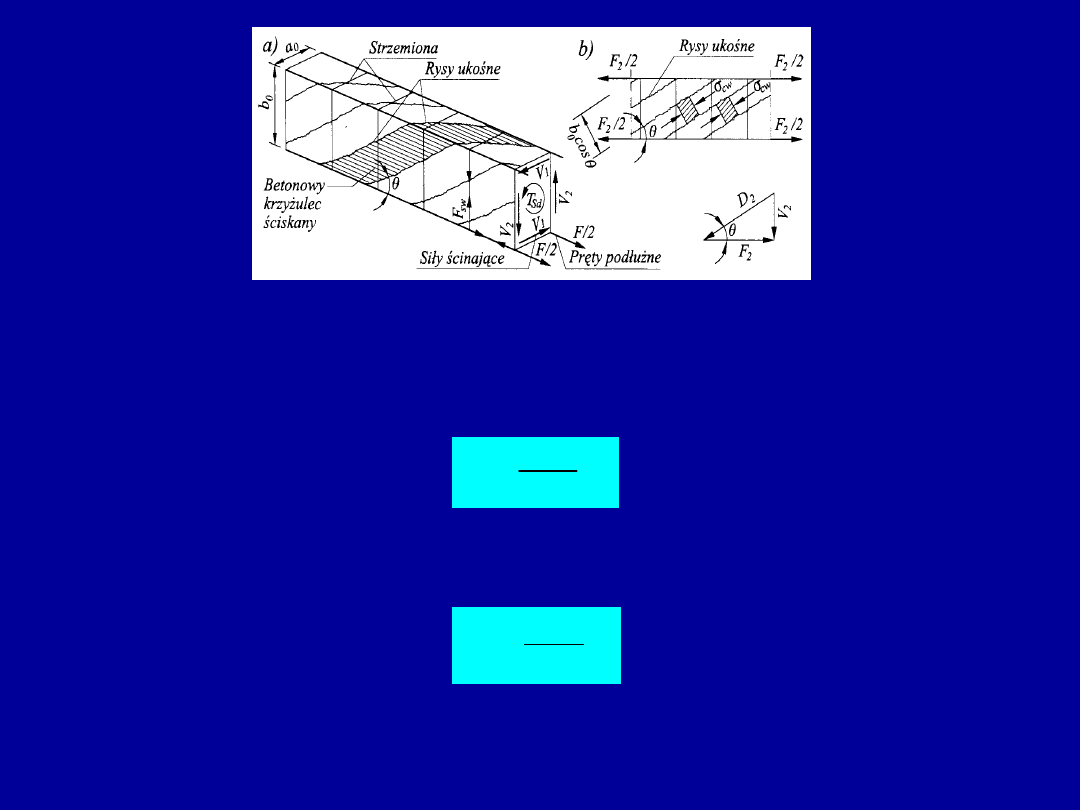
Sumaryczne siły poprzeczne przypadające na przekrój umownej kratownicy to:

- siły

V

2

na bocznych powierzchniach elementu

- siły

V

1

na górnej lub dolnej powierzchni elementu

0

1

2

a

A

T

V

k

Ed



0

2

2

b

A

T

V

k

Ed



13

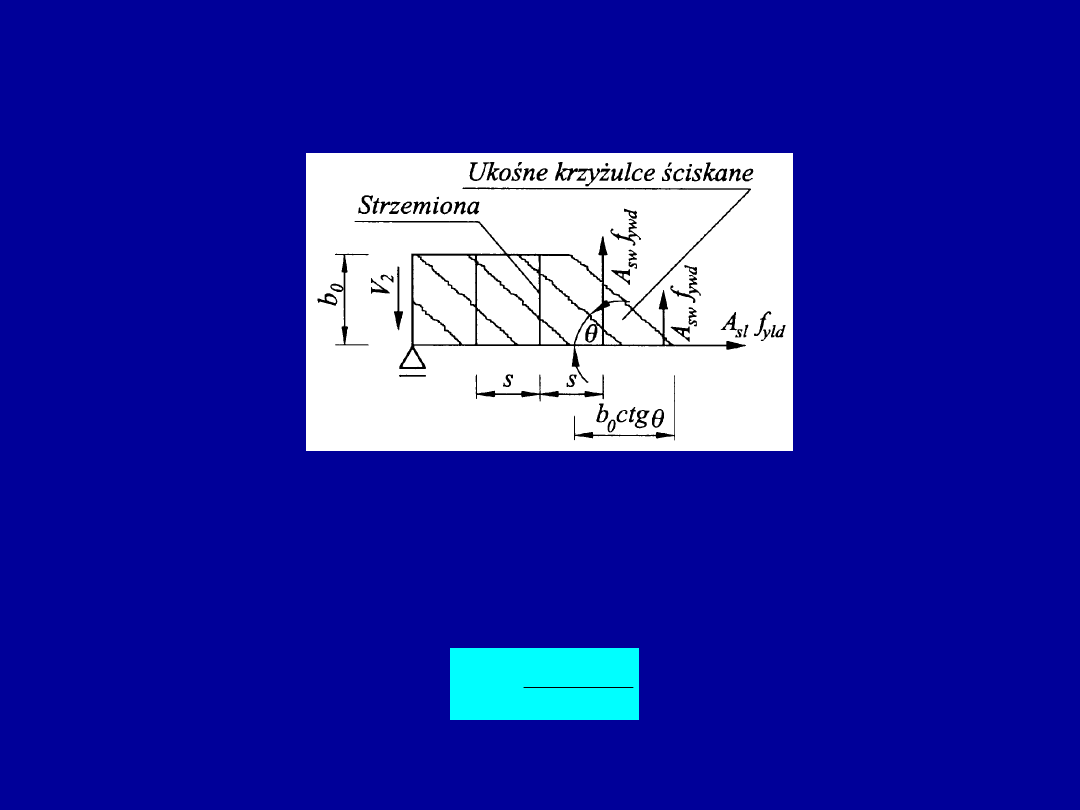
Rysy ukośne i krzyżulce ściskane w ścianie kratownicy przestrzennej

Widoczny fragment przekroju wydzielonego z przestrzennej kratownicy pozostaje
w równowadze pod działaniem sił w strzemionach pionowych przeciętych przekrojem
ukośnym wzdłuż rysy nachylonej pod kątem

. Liczbę strzemion o rozstawie s,

przeciętych przekrojem na odcinku o długości b

0

ctg

 obliczymy ze wzoru

s

b

n

s



ctg

0



Kąt

. przyjmuje się według tych samych zasad jak w obliczeniach na siłę poprzeczną

14

Obliczenia wg modelu

kratownicowego

Suma sił rozciągających w gałęziach strzemion (po osiągnięciu przez stal granicy
plastyczności f

ywd

) równoważy wypadkową pionową naprężeń ścinających V

2

.

2

0

cot

V

s

b

f

A

F

ywd

sw

sw









A

sw

– oznacza pole przekroju jednej gałęzi strzemienia pracującego na skręcanie.

Przekształcając powyższe wyrażenia możemy określić
potrzebne pole przekroju strzemion pionowych na
skręcanie

0

2

2

b

A

T

V

k

Ed





tan

2

ywd

k

Ed

sw

f

A

s

T

A





gdzie

o

k

Ed

o

ywd

sw

sw

b

A

T

s

b

f

A

F









2

cot



15

Siły podłużne wywołane skręcaniem

w modelu kratownicy przestrzennej

W ściankach pionowych modelowej kratownicy siła rozciągająca F

2

równoważy

składową pionową V

2

i ukośnie działającą siłę ściskającą D

2

.

W ściankach poziomych zachodzi analogiczna równowaga między siłami F

1

, V

1

i D

1

Z trójkątów sił w każdej ze ścianek otrzymujemy



cot

2

2

V

F 



cot

1

1

V

F 

16

Obliczenia wg modelu kratownicy

przestrzennej

Całkowita siła podłużna F działa w środku ciężkości ścianek
kratownicy przestrzennej.

Połowę siły rozciągającej F przenoszą pręty podłużne zbrojenia
umieszczone
w narożnikach kratownicy na górnej i na dolnej ściance.











cot

2

2

2

1

2

1

V

V

F

F

F









Z powyższych równań otrzymujemy zapis



cot

2

k

k

Ed

u

A

T

F 

gdzie u

k

- obwód idealizowanego przekroju elementu (obwód rdzenia przekroju);





0

0

2

b

a

u

k





0

1

2

a

A

T

V

k

Ed



0

2

2

b

A

T

V

k

Ed



17

Obliczenia zbrojenia wg modelu

kratownicowego

Zakładając, że podłużne zbrojenie osiąga granicę
plastyczności, odpowiednie pole przekroju zbrojenia
podłużnego na skręcanie A

sl

można określić

Prowadzi to do wzoru na pole przekroju zbrojenia podłużnego na skręcanie

yd

sl

f

A

F







cot

2

yd

k

k

Ed

sl

f

A

u

T

A









cot

2

k

k

Ed

u

A

T

F 

gdzie

18

Nośność elementów poddanych

czystemu skręcaniu

Nośność na skręcanie wyraża opór przekroju kratownicy
modelującej skręcany element żelbetowy. Nośność
dowolnego przekroju pełnościennego ustalana jest jak dla
przekroju cienkościennego

W PN-EN 1992-1-1:2008, wymiarowanie przekrojów w elementach skręcanych
momentem o wartości obliczeniowej T

Ed

ogranicza się do

przedziału

max

,

Rd

Ed

T

T 

A - linia środkowa

B – zewnętrzna krawędź

przekroju efektywnego,

obwód u,

C - otulina

T

Rd,max

–

nośność na skręcanie z uwagi na maksymalny moment

skręcający (wynikający z naprężeń ściskających w krzyżulcach
betonowych kratownicy modelowej)

19

Nośność elementów poddanych czystemu

skręcaniu

Nośność T

Rd,max

określa się przy maksymalnych naprężeniach w krzyżulcach, równych

cd

cw

f



 

Jeżeli strzemiona na skręcanie są prostopadłe (



= 90

0

) to wzór przybiera postać













2

,

,

max

,

cot

1

cot

2

cos

sin

2











k

i

ef

cd

k

i

ef

cd

Rd

A

t

f

A

t

f

T











 



250

1

6

,

0

ck

f



gdzie

20

Zbrojenie podłużne na skręcanie

Otrzymujemy

Pole przekroju dodatkowego

podłużnego

zbrojenia na skręcanie

można wyznaczyć
z przekształcenia wzoru

gdzie ΣA

sl

– sumaryczne pole przekroju zbrojenia podłużnego na skręcanie

f

yd

- obliczeniowa granica plastyczności prętów zbrojenia podłużnego



cot

2

yd

k

k

Ed

sl

f

A

u

T

A









cot

2

k

Ed

k

yd

sl

A

T

u

f

A





21

Nośność przy jednoczesnym skręcaniu i ścinaniu

Jeżeli element poddany jest skręcaniu i sile poprzecznej, naprężenia oblicza się
metodami wytrzymałości materiałów, dodatkowo sprawdzając warunki ograniczenia
w zakresie ściskania betonowych krzyżulców i rozciągania prętów modelujących
strzemiona zastępczej ustroju kratownicy. Jednocześnie należy sprawdzić warunki

1

2

max

,

2

max

,

































Rd

Ed

Rd

Ed

V

V

T

T

gdzie: T

Rd,,max

- nośność przekroju na skręcanie (z uwagi na beton krzyżulców ściskanych)

V

Rd,max

– maksymalna siła poprzeczna w przekroju w krzyżulcach ściskanych

W złożonym stanie obciążeń pole przekroju strzemion wyznacza się niezależnie
ze względu na ścinanie oraz na czyste skręcanie.

22

Nośność przy jednoczesnym skręcaniu i zginaniu

W tym przypadku zbrojenie podłużne należy projektować oddzielnie
na każdy rodzaj oddziaływań. Obowiązują tu następujące zasady:

W strefie rozciąganej przekroju zbrojenie podłużne na skręcanie
musi być obliczone dodatkowo ponad zbrojenie na zginanie,

W strefie ściskanej (w wyniku zginania) zbrojenie podłużne na zginanie
nie wymaga uzupełnienia o pręty podłużne obliczane na skręcanie,
gdy naprężenia od skręcania są mniejsze od naprężeń ściskających od zginania.

23

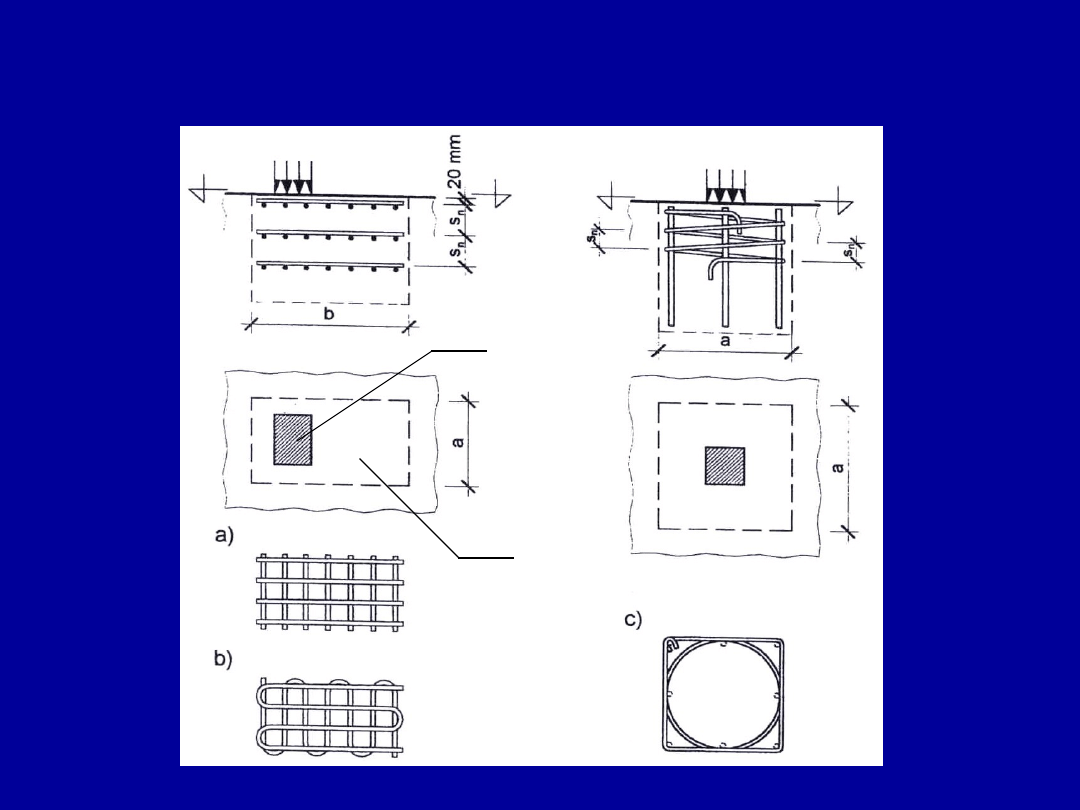
Zasady zbrojenia elementów skręcanych

Zbrojenie elementów poddanych czystemu skręcaniu lub skręcaniu
połączonemu ze ścinaniem powinno składać się z dwuramiennych
zamkniętych strzemion i dodatkowych prętów podłużnych
umieszczonych równomiernie na obwodzie rdzenia elementu.
Strzemion czteroramiennych nie stosuje się z uwagi na to, że ich
wewnętrzne ramiona pozostają poza zastępczą grubością t

ef

ścianki

elementu i nie przenoszą naprężeń

a1) a2) a3)

a) kształty zalecane

b) kształt nie

zalecany

Rozstaw prostopadłych strzemion
powinien nie przekraczać wartości:

8

u

d

75

,

0

b

24

Przykład elementu skręcanego

M

Ed

[kNm]

V

Ed

[kN]

T

Ed

[kNm]

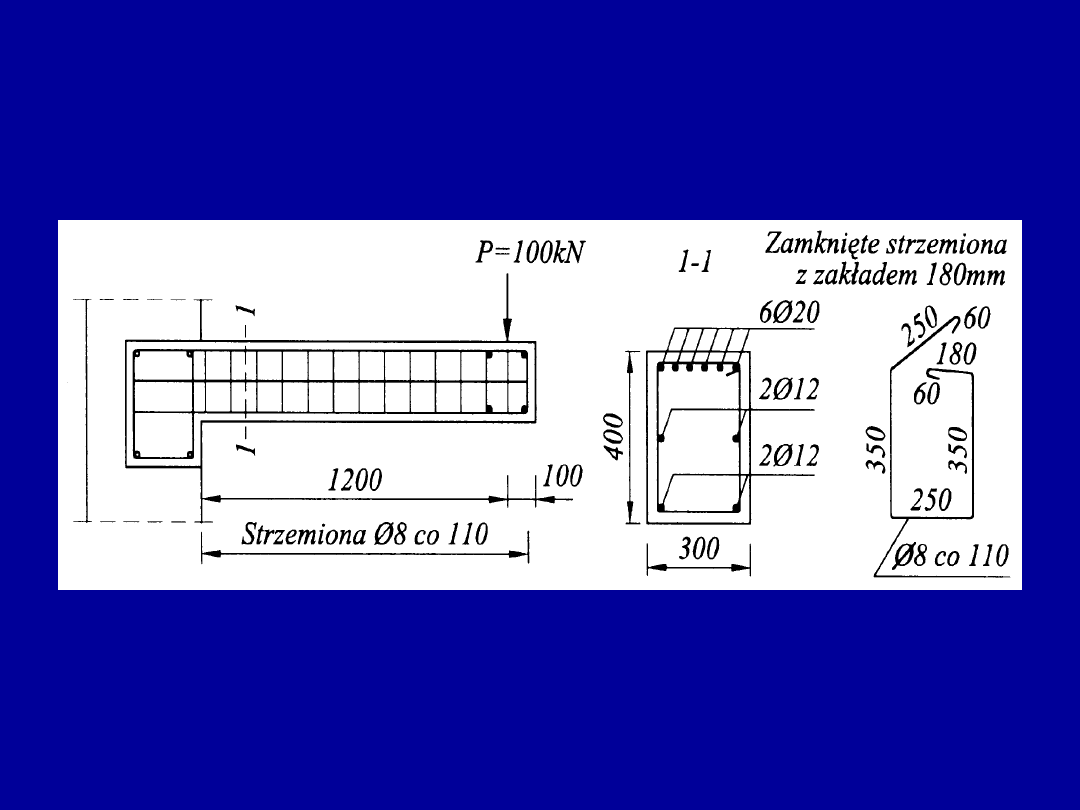
25

Przykład zbrojenia elementu skręcanego

26

Docisk przy obciążeniach

miejscowych

wg PN-EN 1992-1-1

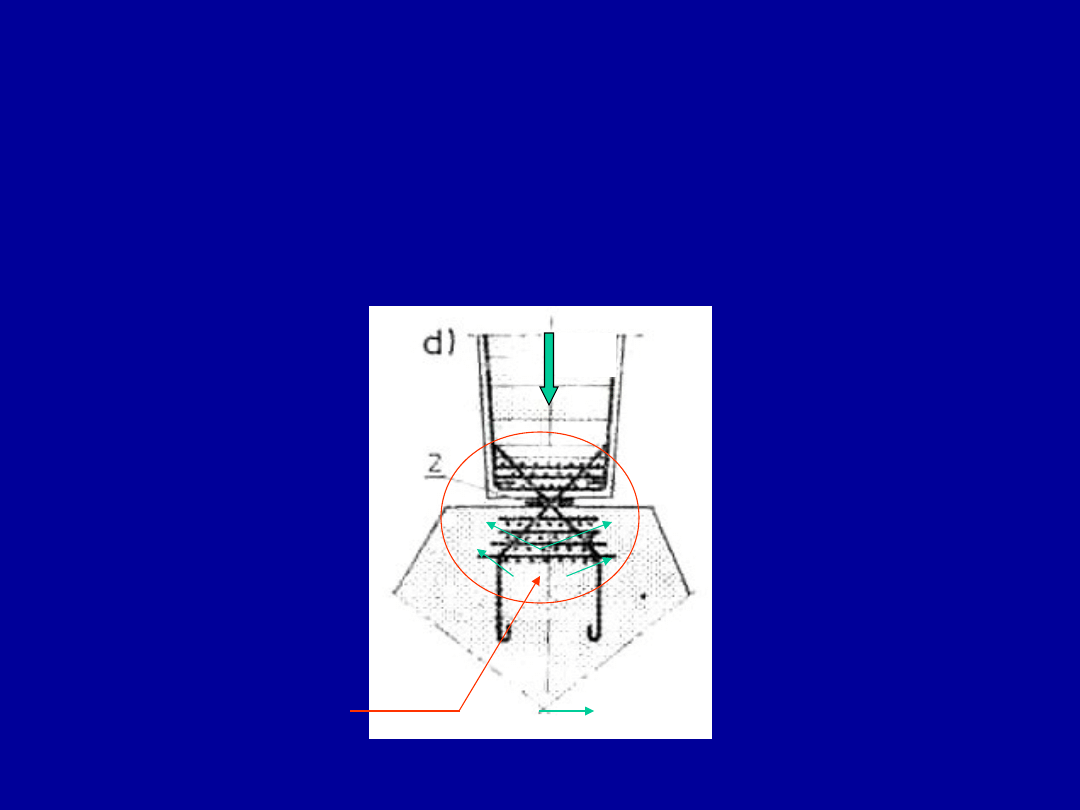
27

Przykład występowania docisku w strefie

przegubu słupa w połączeniu z

fundamentem

Strefa
docisku

N

Ed

Linie
rozciągań

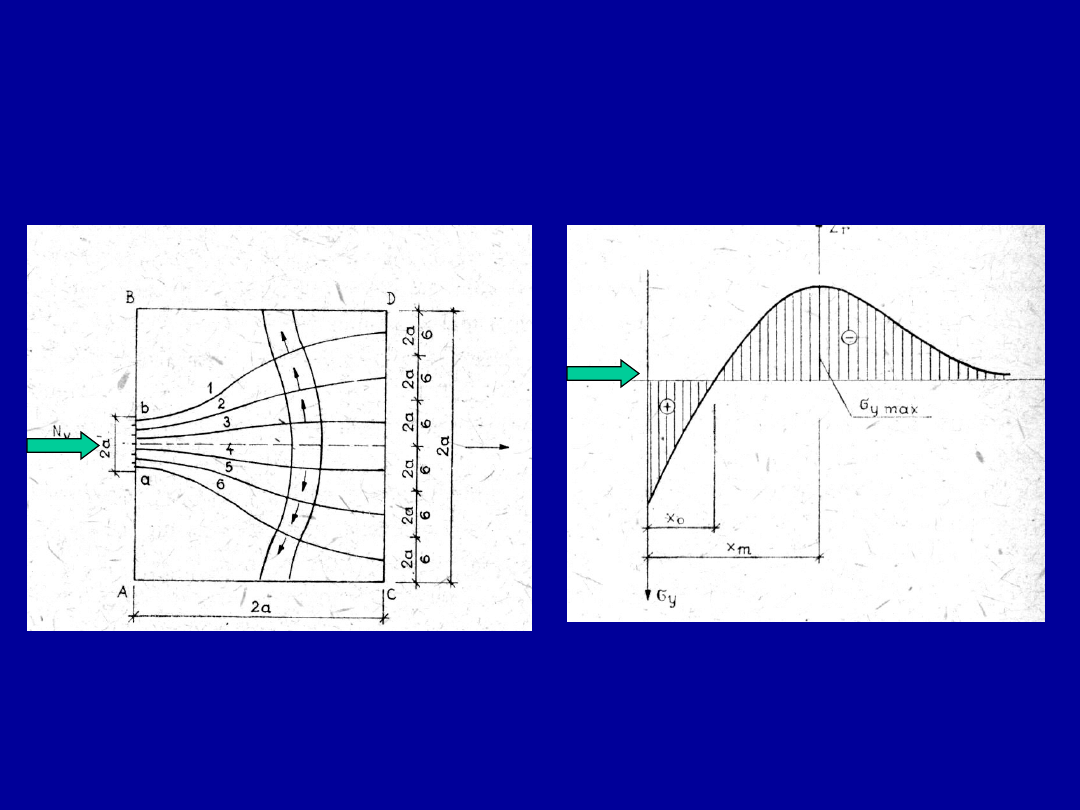
28

Przestrzenny stan naprężeń

wywołanych miejscowym dociskiem

Efekty miejscowego docisku: a) – ściskanie w kierunku x,

b) ściskanie i rozciąganie w kierunku y

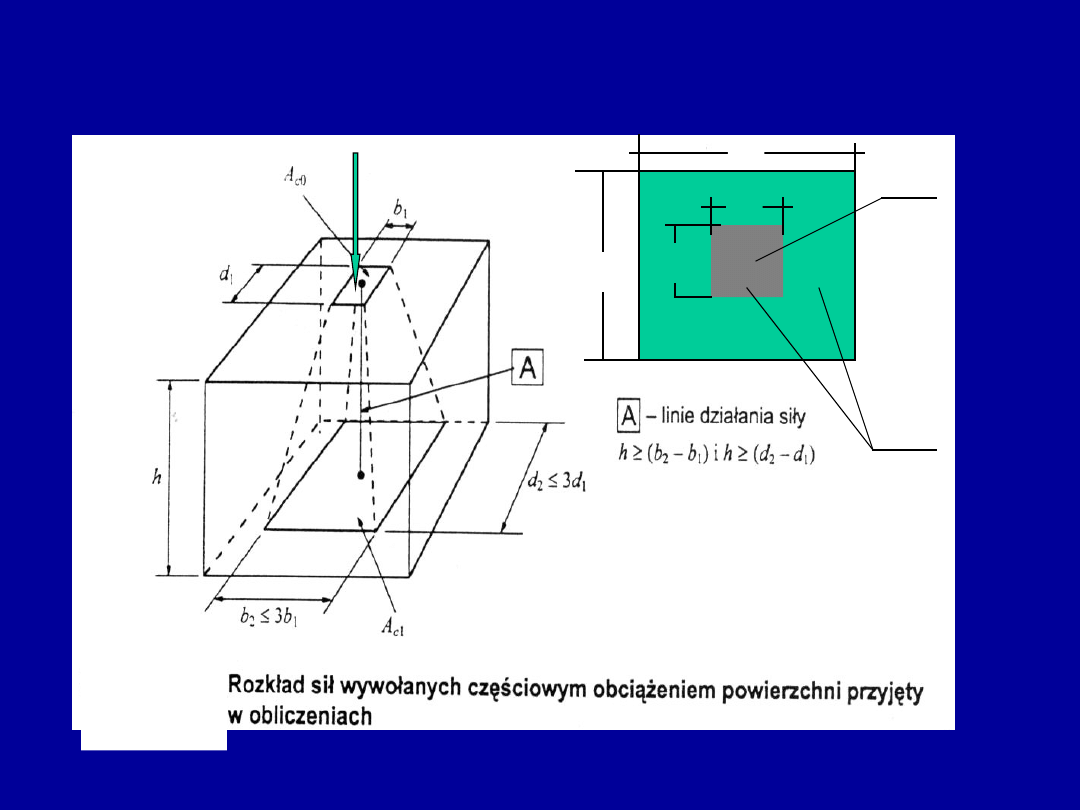
29

Poprzeczne obciążenie powierzchni

elementu

(problem docisku)

A

c0

A

c1

d

1

d

2

b

1

b

2

30

Nośność elementu bez zbrojenia

na docisk

gdzie: A

co

– powierzchnia docisku

A

c1

- największa obliczeniowa powierzchnia rozdziału

o kształcie podobnym do A

co

0

0

3

c

cd

c

cd

Rdu

A

f

A

f

F







3

0

1





c

c

A

A



gdzie

31

Rodzaje zbrojenia poprzecznego elementu

na docisk

5

,

1



k

A

c0

A

c1

32

Nośność elementu zbrojonego

poprzecznie na docisk – zbrojenie

siatkami

gdzie: k - współczynnik mocy zbrojenia na docisk

u

yd

cd

Rd

Ed

A

kf

A

f

V

V







0



n

st

st

u

s

A

l

n

A

l

n

A

2

,

2

2

1

,

1

1





Jeżeli zbrojenie na docisk jest wykonane
z siatek zgrzewanych lub wyginanych

5

,

1



k

33

Zbrojenie na docisk z siatek zgrzewanych lub wyginanych

n

st

st

u

s

A

l

n

A

l

n

A

2

,

2

2

1

,

1

1





5

,

1



k

gdzie:

n

1

, n

2

, l

1

, l

2

, A

st,1

, A

st,2

- odpowiednio liczba, długość

i pole przekroju pręta siatki w obydwu kierunkach

s

n

– rozstaw siatek

34

Koniec wykładu 8