1

Obliczeniowa kontrola 

zarysowania elementów

 

żelbetowych

WYKŁAD Nr 9

PODSTAWY 

PROJEKTOWANIA 

KONSTRUKCJI 

ŻELBETOWYCH

Semestr V , r .ak. 2011/2012

Opracowanie - prof. dr hab. inż. Andrzej Łapko

 

 

2

Wprowadzenie – mechanizm 

pojawienia się rys

 

Rysy powstają w rezultacie osiągnięcia przez beton wytrzymałości na rozciąganie, 

w określonych przekrojach i strefach elementów żelbetowych.

Naprężenia pochodzące od zewnętrznych czynników:

• mechanicznych (ciężar własny, obciążenia użytkowe) 

• niemechanicznych (zmiany temperatury, osiadanie podpór) 

Powstawanie rys jest w żelbecie praktycznie nieuniknione, zatem na etapie 
projektowania należy przeprowadzać kontrolę stanu granicznego zarysowania.

 

 

3

Rysy w betonie – problem szczelności i 

trwałości konstrukcji

 

 

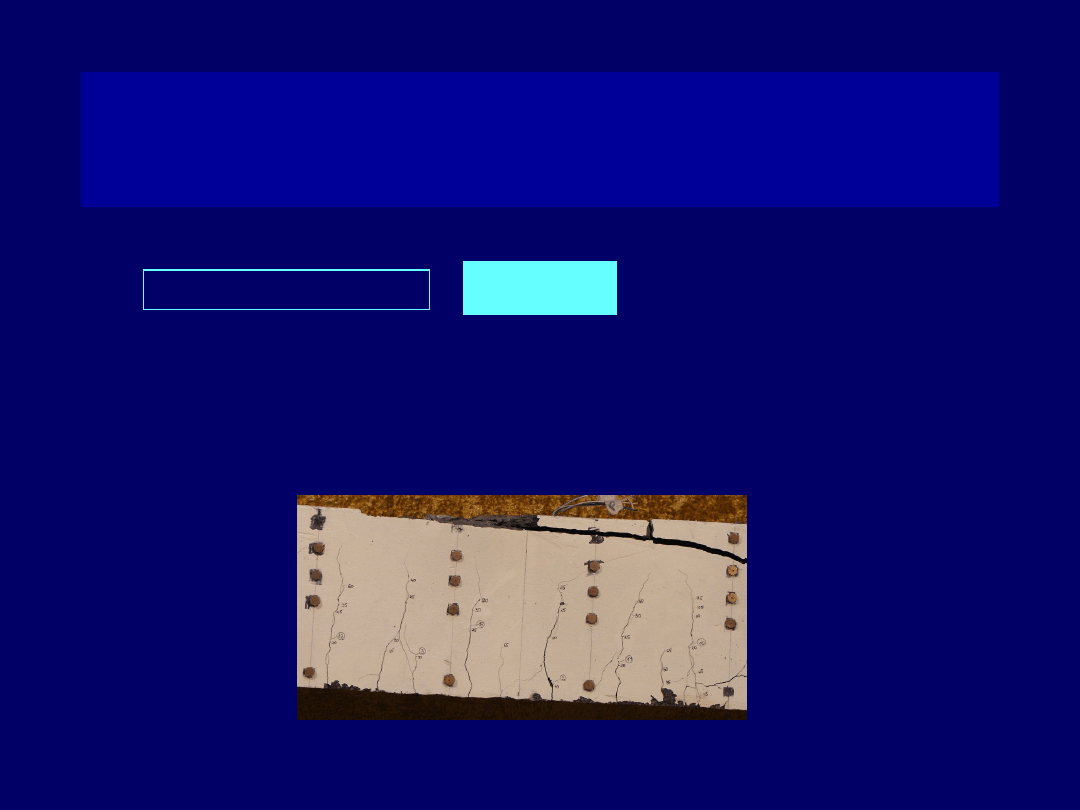
4

Zarysowana strefa rozciągana zginanej belki 

żelbetowej       w chwili zniszczenia elementu, 

Strefa ściskana

 

 

5

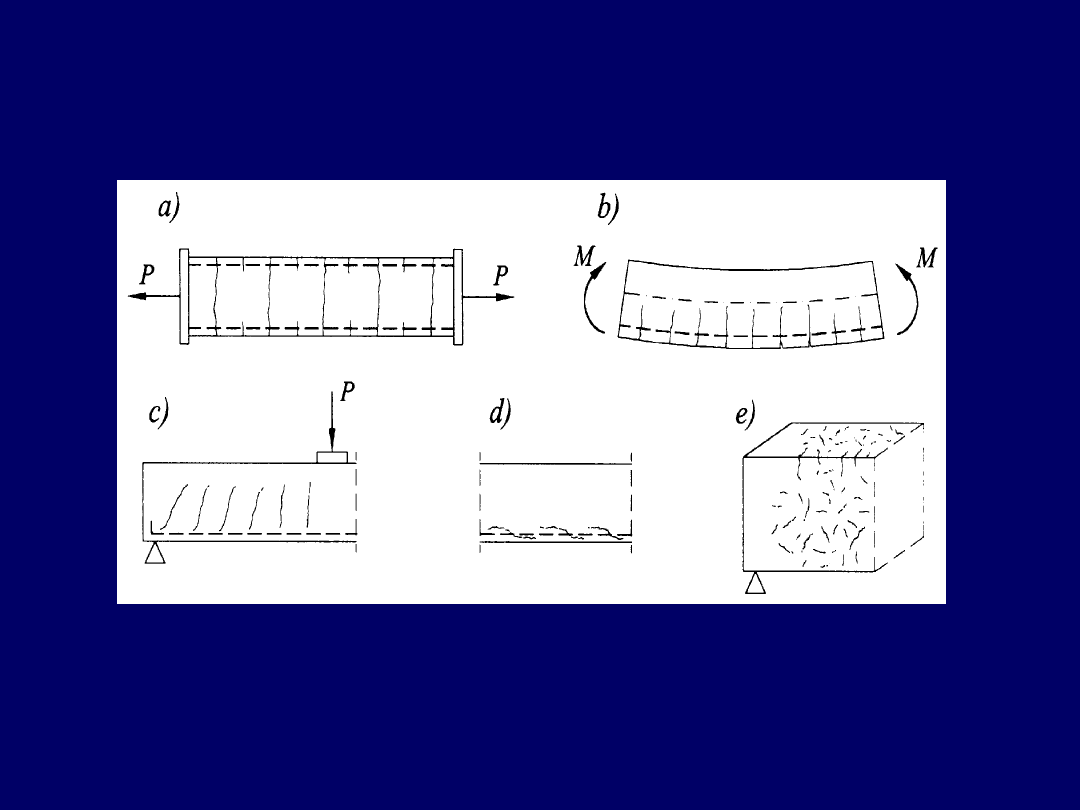
Przykładowe mechanizmy powstawania rys 

w konstrukcjach żelbetowych

Rysy strukturalne: a) prostopadłe, przebiegające „na wylot” (przy rozciąganiu), 
b) rysy prostopadłe przy zginaniu, c) rysy ukośne od sił poprzecznych,
d)      rysy podłużne wzdłuż zbrojenia , e) rysy powierzchniowe (od skurczu)

 

 

6

Obliczeniową kontrolę rys prowadzimy 

w ramach stanu granicznego 

użytkowalności konstrukcji

 

 

7

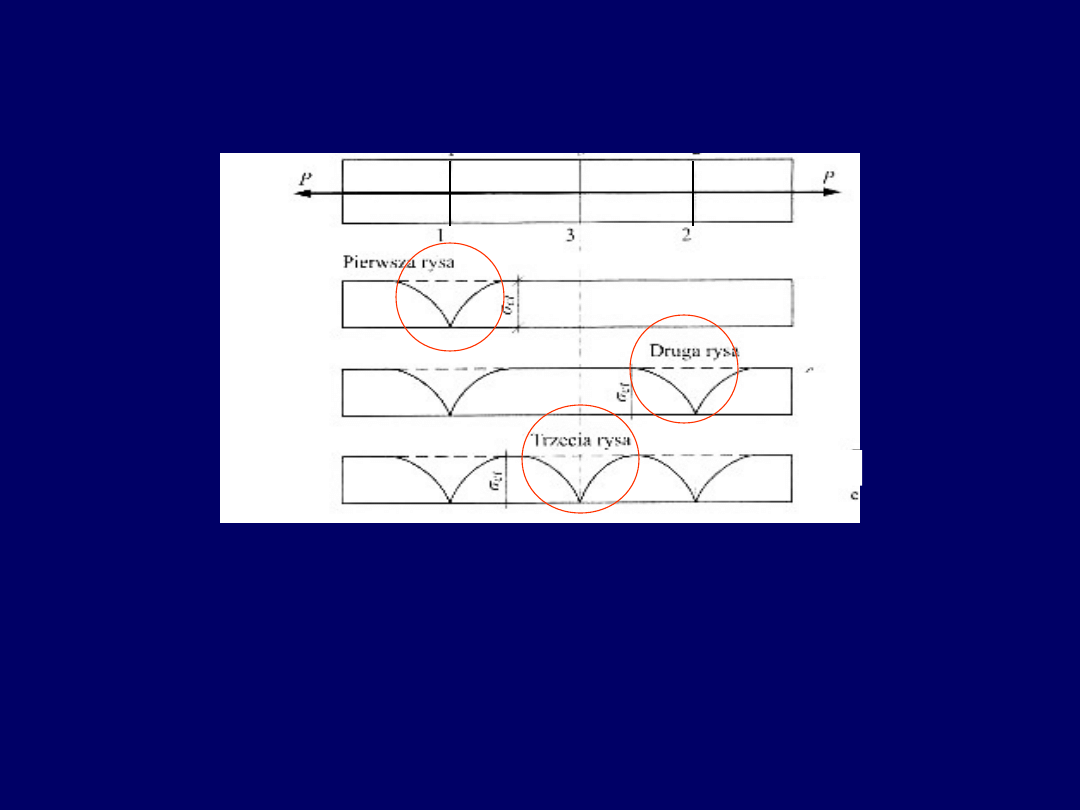
Proces powstawania rysy w przekroju żelbetowym osiowo 
rozciąganym

Wytrzymałość betonu na rozciąganie f

ct 

nie jest stała na długości elementu 

(wskutek losowo zróżnicowanej struktury betonu). 

Pierwsza rysa wystąpi w tym przekroju, gdzie 



ct

 = f

ct

 (przekrój 1-1). Po powstaniu

rysy w przekroju 1-1 naprężenia w betonie spadają do zera, a siłę rozciągającą 
przejmuje zbrojenie, z uwagi na przyczepność zbrojenia do betonu. 

f

ctm

f

ctm

F

ctm   

 

 

8

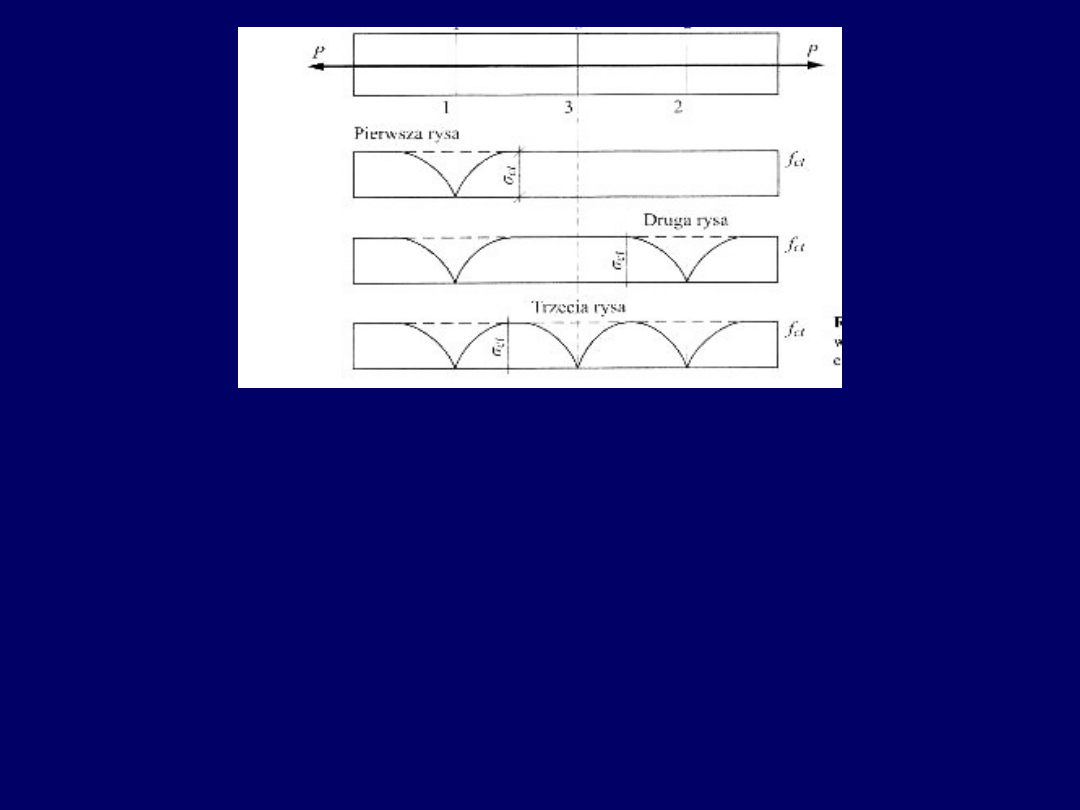
W  bliskim  sąsiedztwie  rysy  naprężenia  w  betonie  ulegają 
redystrybucji.  Dalszy  przyrost  obciążenia  spowoduje  w  innym 
przekroju  elementu  osiągnięcie  przez  beton  wytrzymałości  f

ct

  - 

dojdzie  zatem  do  powstania  drugiej  rysy  (przekrój  2-2). 

Wraz  z  przyrostem  obciążenia  wystąpi  dalsza  redystrybucja 
naprężeń  w  betonie  i  powstanie  kolejna  trzecia  rysa  między 
pierwszą i drugą. 

 

 

9

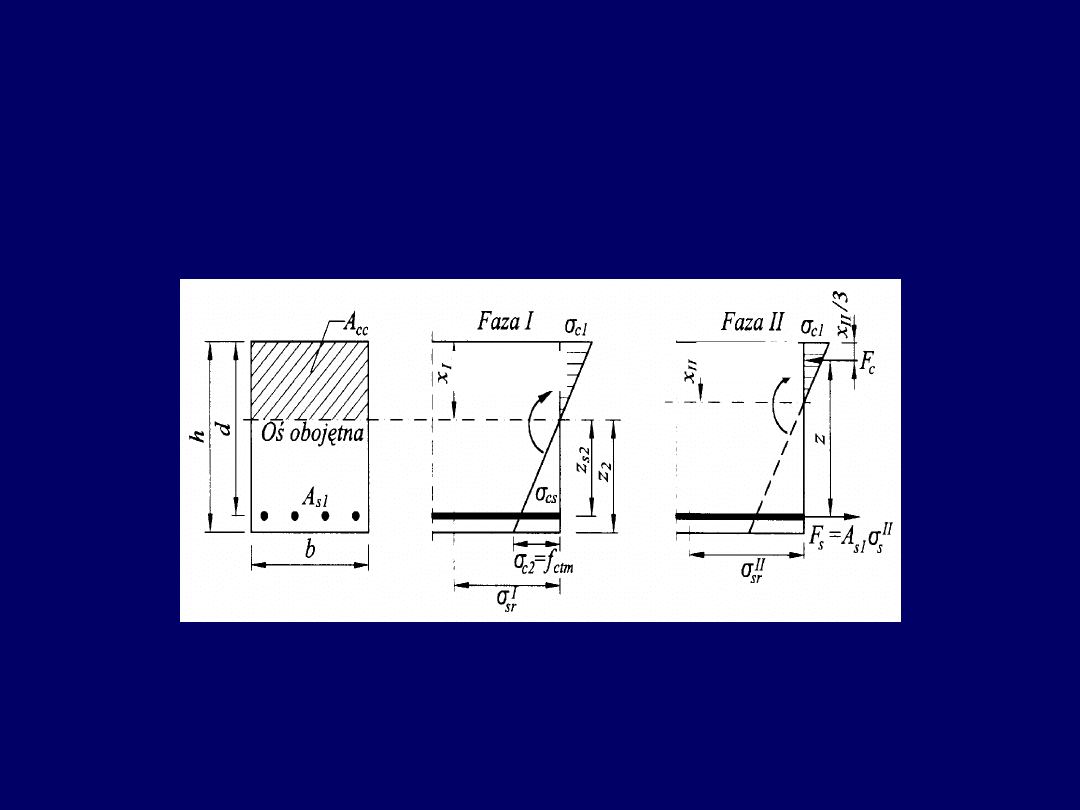
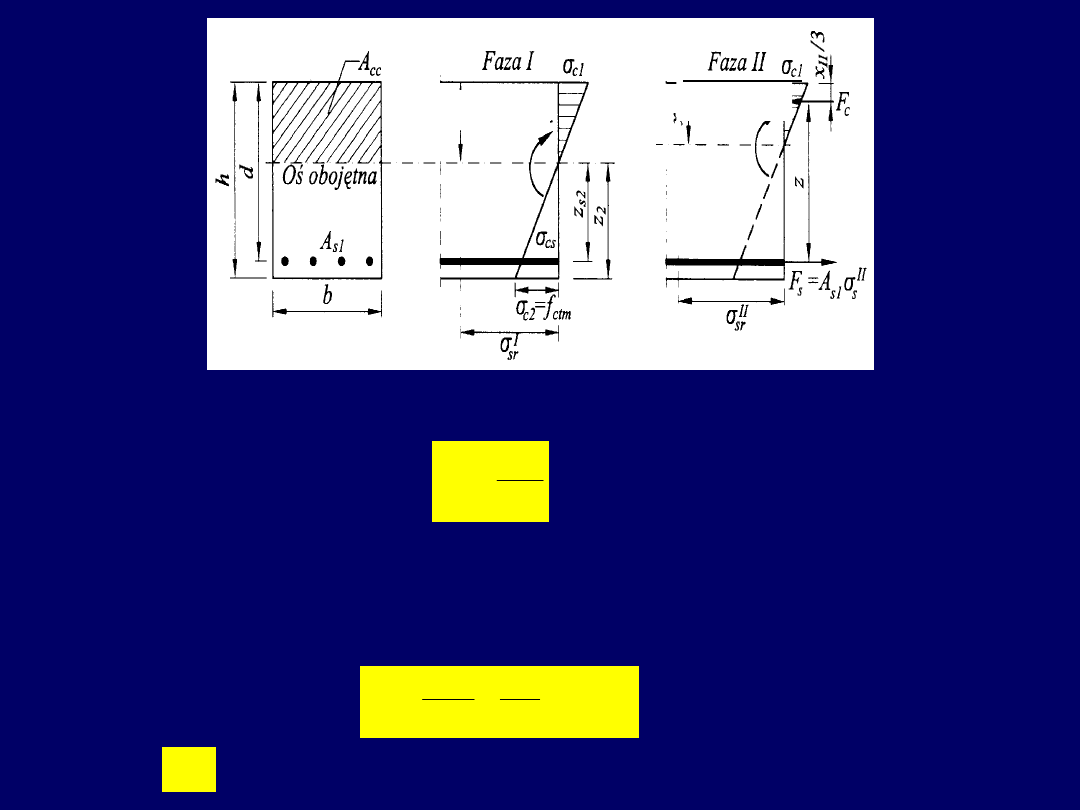
Zastosowanie teorii sprężystości 

w obliczeniach stanu zarysowania

Faza I

Faza II

Momenty statyczne, wskaźniki wytrzymałości, momenty bezwładności, położenie 
osi obojętnej, a także naprężenia w betonie i zbrojeniu można wyznaczać według 
metody naprężeń liniowych (NL).

M

Ed.

=M

cr

M

Ed.

=M

cr

Przed powstaniem rysy

Po powstaniu rysy

 

 

10

Pod obciążeniem 

doraźnym 

współpracę betonu i zbrojenia

 

charakteryzuje współczynnik 



e

 

cm

s

e

E

E





gdzie: E

s

 – moduł sprężystości stali zbrojeniowej

 

Przy obciążeniu 

długotrwałym 

relację między odkształcalnością stali i betonu 

zapisuje się za pomocą współczynnika





0

,

,

,

1

t

cm

s

ef

c

s

t

e

E

E

E

E













gdzie  -       końcowy współczynnik pełzania betonu

 

0

,t





M

Ed.

=M

cr

M

Ed.

=M

cr

 

 

11

Przekrój osiowo rozciągany - siła 

rysująca N

cr

W fazie I (tuż przed zarysowaniem) siłę powodującą powstanie rysy 
(tzw. siłę rysującą) w elemencie osiowo rozciąganym obliczamy ze wzoru 

c

ctm

c

ct

cr

A

f

A

N







gdzie  f

ctm 

– średnia wytrzymałość betonu na rozciąganie,

          A

c

 – pole przekroju poprzecznego elementu.

 

 

12

Przekrój zginany prostokątny – moment 

rysujący M

cr

gdzie:   J

c

 – moment bezwładności przekroju tuż przed powstaniem rysy,

            W

ct

 - wskaźnik wytrzymałości przekroju względem krawędzi rozciąganej.

Zarysowanie  wywołuje  moment  zginający  M

cr

  (tzw.  moment 

rysujący), 
który  w  elemencie  o  przekroju  prostokątnym  i  wymiarach  h  x  b 
można zapisać

6

2

2

2

2

bh

f

W

z

J

M

ctm

ct

c

c

c

cr











M

Ed.

=M

cr

M

Ed.

=M

cr

 

 

13

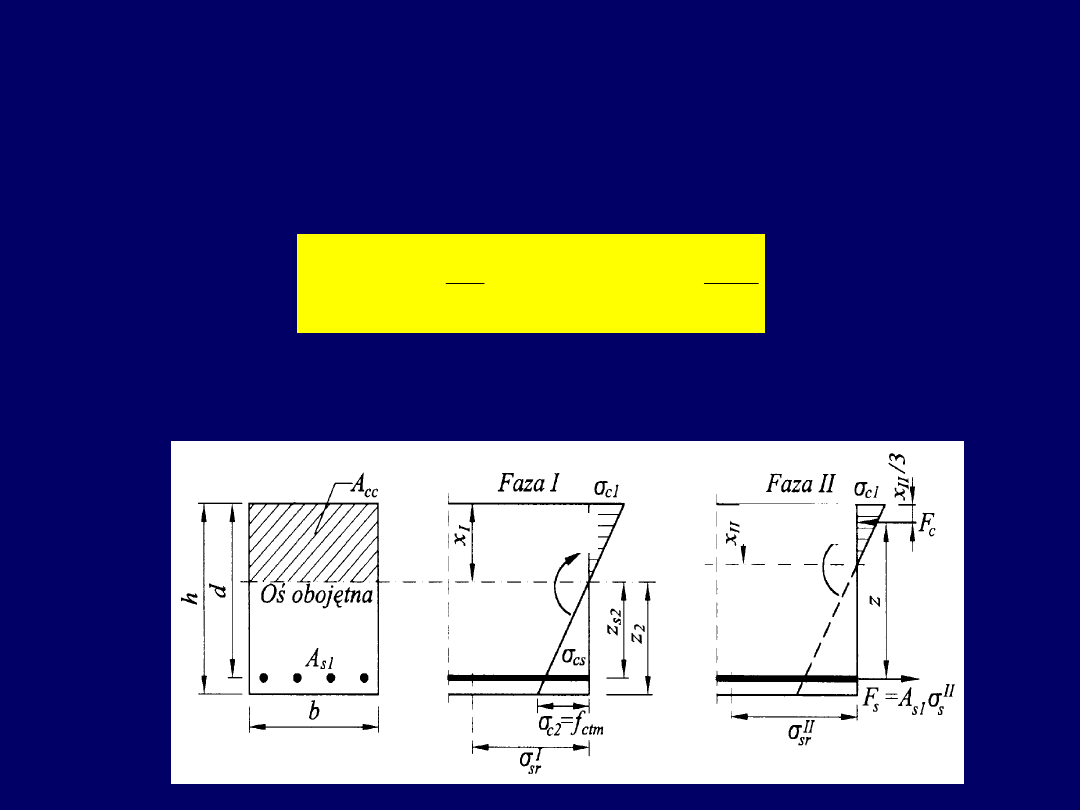
Naprężenia w przekroju elementu w II-

giej fazie

Położenie osi obojętnej x w przekroju wg teorii naprężeń liniowych oblicza się 
z równania sumy momentów statycznych pól powierzchni strefy ściskanej A

cc

 

i przekroju zbrojenia rozciąganego A

s1

. 

Zgodnie z teorią liniowej sprężystości  uwzględnia 
się 
tzw. sprowadzone pole przekroju zbrojenia

1

1

s

cm

s

s

e

A

E

E

A 



Równanie sumy momentów statycznych względem osi obojętnej przekroju ma postać





0

2

1

2







II

s

e

II

x

d

A

bx































 



e

s

e

s

e

s

II

bd

A

bd

A

bd

A

d

x







1

1

1

2

1

s

e

c

cs

A

A

A









gdzie

x

II

A

s1

=

b

α

e

A

s1

d

z = d - x

II

/3

A

s1

 σ

s

 

 

14

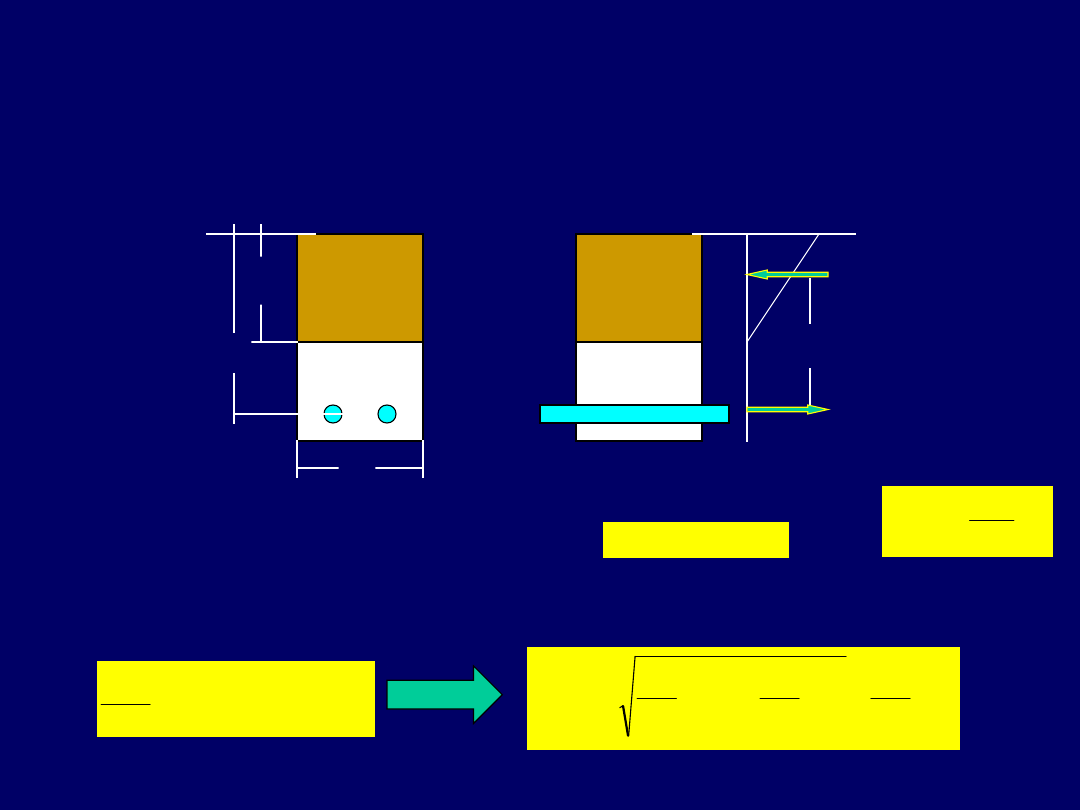
Naprężenia w przekroju elementu 

zginanego

w II-giej fazie pracy

Równanie sumy momentów statycznych względem osi obojętnej przekroju ma postać





0

2

1

2







II

s

e

II

x

d

A

bx











e

e

e

II

d

x













2

gdzie   

  -         stopień zbrojenia rozciąganego elementu.

 

Z równania równowagi wypadkowych sił w betonie i zbrojeniu otrzymujemy 
wzór na naprężenia w zbrojeniu elementu zginanego (w czystej fazie II) 











 



3

1

II

s

Ed

s

x

d

A

M



bd

A

s1





 

 

15

Normowe wymagania w zakresie 

ograniczania szerokości rys

max

w

w

k



gdzie:  w

k

  – obliczeniowa szerokość rysy,

            w

max

– graniczne rozwarcie rysy [mm]

Według Eurokodu 2

 

 

16

Wymagania ograniczania szerokości rys wg 

Eurokodu 2

max

w

w

k



Klasa 

ekspozycji

środowiska

Elementy żelbetowe i 

sprężone cięgnami bez 

przyczepności

Elementy sprężone 

cięgnami z 

przyczepnością

Kombinacja obciążeń 

prawie stała

Częsta kombinacja 

obciązeń

XO, XC1

0,4

1)

0,2

XC2, XC3, 
XC4

0,3

0,2

XD1, XD2, 
XS1,
XS2, XS3

Dekompresja

1)

Dla klas X0 i XC1 rysa nie ma wpływu na trwałość, ograniczenie podaje się aby zachować odpowiedni wygląd elementu

 

 

17

Eurokodu 2

Eurokodu 2

Klasa ekspozycji

Opis klasy ekspozycji

Brak ryzyka korozji lub agresji chemicznej

X0

W betonie niezbrojonym, gdy brak jest zagrożenia efektem zamrażania 
– odmrażania, ścierania lub korozji chemicznej
w warunkach bardzo niskiej wilgotności powietrza 

Korozja wywołana przez karbonatyzację

XC1

Środowisko suche lub stale mokre

XC2

Środowisko mokre, rzadko suche

XC3 – XC4

Umiarkowana wilgotność lub cykliczne mokre i suche

Korozja wywołana chlorkami nie pochodzącymi z wody morskiej

XD1

Umiarkowana wilgotność

XD2

Mokre, sporadycznie suche

XD3

Cyklicznie mokre i suche

Korozja spowodowana chlorkami z wody morskiej

XS1

Środowisko narażone na działanie soli zawartej w powietrzu 
(bez kontaktu z wodą morską)

XS2

Stałe zanurzenie w wodzie morskiej

XS3

Środowisko  w  obszarze  pływów  morza,  rozbryzgów  wody  i 
pyłu wodnego

Wpływy zamrażania i odmrażania wody

XF1

Umiarkowane nasycenie wodą bez środków odladzających

XF2

Umiarkowane nasycenie wodą ze środkami odladzającymi

XF3

Duże nasycenie wodą bez środków odladzających

XF4

Duże nasycenie wodą ze środkami odladzającymi

Agresja chemiczna

XA1

Środowisko słabo agresywne chemicznie wg PN-EN 206-1

XA2

Środowisko średnio agresywne chemicznie wg PN-EN 206-1

XA3

Środowisko silnie agresywne chemicznie wg PN-EN 206-1

Klasy 
ekspozycji 
środowiska 
budowli
wg Eurokodu 2

 

 

18

Kontrola uproszczona rys (bez 

obliczeń) 

wg Eurokodu 2

Dla żelbetowych płyt poddanych zginaniu bez udziału rozciągających sił 
podłużnych, nie wymaga się specjalnych obliczeń dla kontroli zarysowania
Jeżeli grubość całkowita nie przekracza 200 mm i zastosowano odpowiednie 
przepisy w zakresie konstruowania

gdzie

 

s 

i  s

max

 odczytuje się z tabel

   

s

 

Podejście wymaga ograniczenia średnicy prętów głównych na zginanie 
i ich rozstawu na długości elementu

s   

s

max

 

dla belek

dla płyt

 

 

19

Maksymalna średnica pręta 



s

*

 

przy kontroli rys wg Eurokodu 2

Naprężenie w 

stali

[MPa]

Maksymalna średnica pręta [mm]

w

k

 = 0,4 mm

w

k

 = 0,3 mm

w

k

 = 0,2 mm

160

40

32

25

200

32

25

16

240

20

16

12

280

16

12

8

320

12

10

6

360

10

8

5

400

8

6

4

450

6

5

-

 

 

20

Maksymalny rozstaw prętów s (w płytach) przy kontroli rys wg 

Eurokodu 2

Naprężeni

e w stali*

[MPa]

Maksymalny rozstaw prętów [mm]

w

k

 = 0,4 
mm

w

k

 = 0,3 
mm

w

k

 = 0,2 
mm

160

300

300

200

200

300

250

150

240

250

200

100

280

200

150

50

320

150

100

-

360

100

50

-

 

 

21

Kontrola uproszczona stanu zarysowania wg 

Eurokodu 2

Maksymalną średnicę pręta 



s

*

 odczytaną z tablicy 

należy skorygować następująco:

W elementach zginanych

d)

-

2(h

h

k

9

,

2

cr

c

,

*















ef

ct

s

s

f





W elementach rozciąganych (osiowo)

d)

-

8(h

h

9

,

2

cr

,

*















ef

ct

s

s

f





gdzi
e

*

s



s



Skorygowana maksymalna średnica pręta

*

s



Maksymalna średnica pręta przyjęta z tabeli

d

h,

cr

h

Całkowita i efektywna wysokość elementu

Wysokość strefy rozciąganej tuż przed zarysowaniem

ef

ct

f

,

Średnia wytrzymałość betonu na rozciąganie, w chwili spodziewanego 
zarysowania

c

k

Współczynnik uwzględniający kształt wykresu naprężeń przed zarysowaniem

 

 

22

Korekta maksymalnej średnicy pręta:

Elementy zginane

d)

-

2(h

h

k

9

,

2

cr

c

,

*



















ef

ct

s

s

f





Elementy rozciągane

d)

-

8(h

h

9

,

2

cr

,

*















ef

ct

s

s

f





gdzi
e

*

s



4

,

0



c

k

c

k

0

,

1



c

k

Dla czystego rozciągania

Dla zginania

Kontrola uproszczona stanu 

zarysowania 

wg Eurokodu 2

Współczynnik uwzględniający kształt wykresu naprężeń przed zarysowaniem

 

 

23

Obliczanie szerokości rys 

w elementach zginanych

 

 

24

Obliczanie szerokości rys wg PN-B-

03264:2002

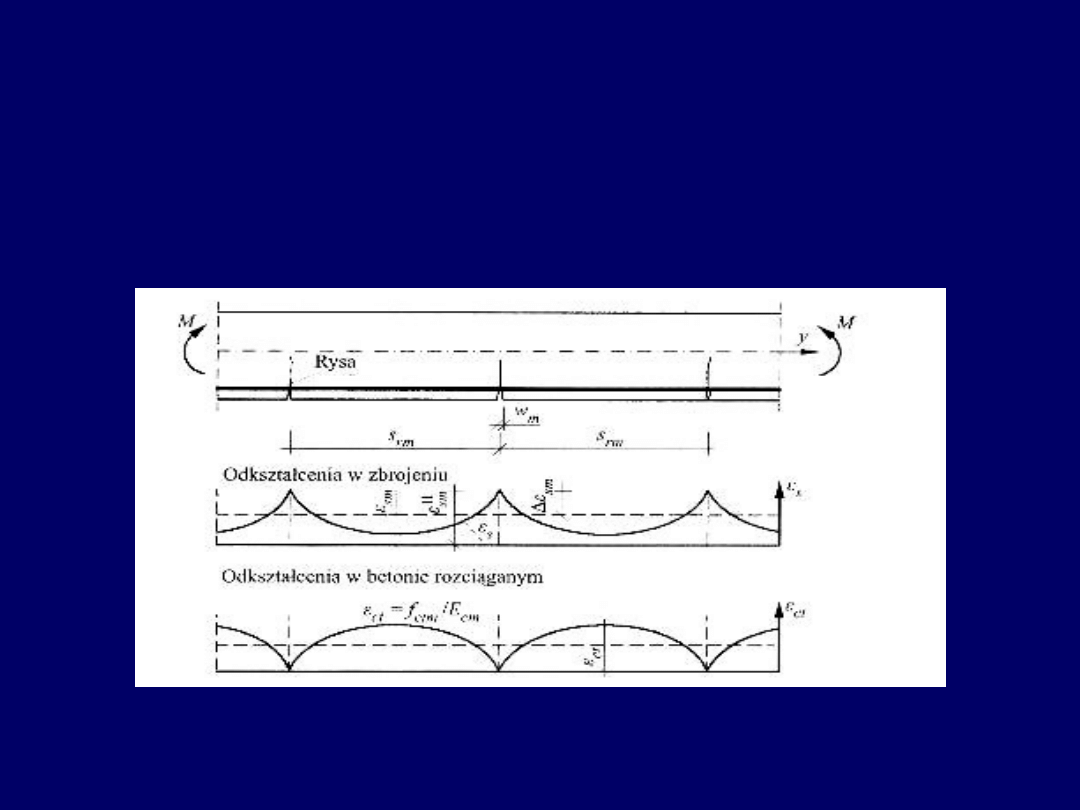
Szerokość rys prostopadłych do osi elementu oblicza się na podstawie 
uśrednionych wartości odkształceń w betonie i stali zbrojeniowej. 

Odkształcenia w zbrojeniu i betonie rozciąganym w chwili powstania rysy

 

 

25

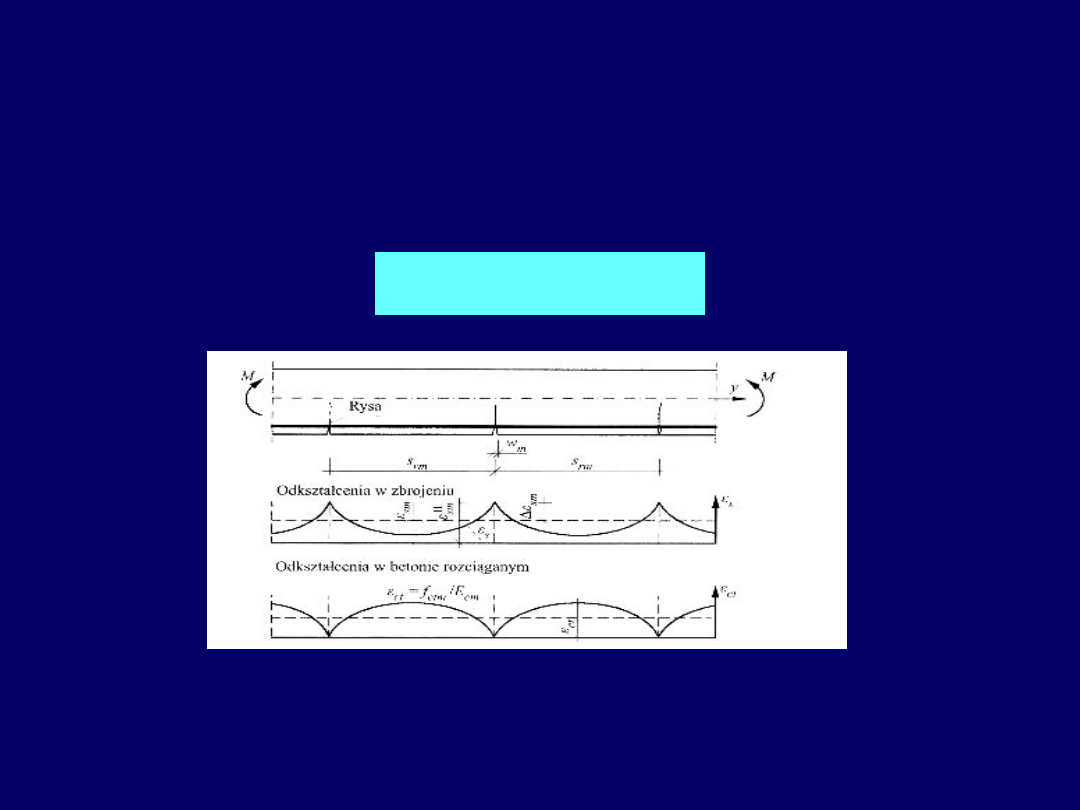
Górny wykres dotyczy odkształceń zbrojenia rozciąganego elementu, dolny zaś – 
odkształceń betonu. Na odcinku między rysami odkształcenia zbrojenia 
są mniejsze od odkształceń w przekroju przez rysę. 

Całkując różnicę odkształceń zbrojenia 



s

 i betonu 



ct

 na odcinku s

rm 

między rysami, 

wyznaczamy średnią szerokość rysy





y

w

rm

s

cm

sm

k

d











 

 

26

Średnią szerokość rozwarcia rysy obliczamy jako iloczyn maksymalnego rozstawu 
rys s

r,max

 i różnicy średnich odkształceń zbrojenia 



sm 

(z uwzględnieniem efektu 

usztywnienia przy rozciąganiu 

(tension stiffening effect

) i średnich odkształceń betonu

 

w przekroju między rysami 

Odkształcenia zbrojenia 



sm 

(w fazie II) 

oblicza się 
w funkcji naprężeń w przekroju 
zarysowanym.





cm

sm

r

k

s

w









max

,

 

 

27

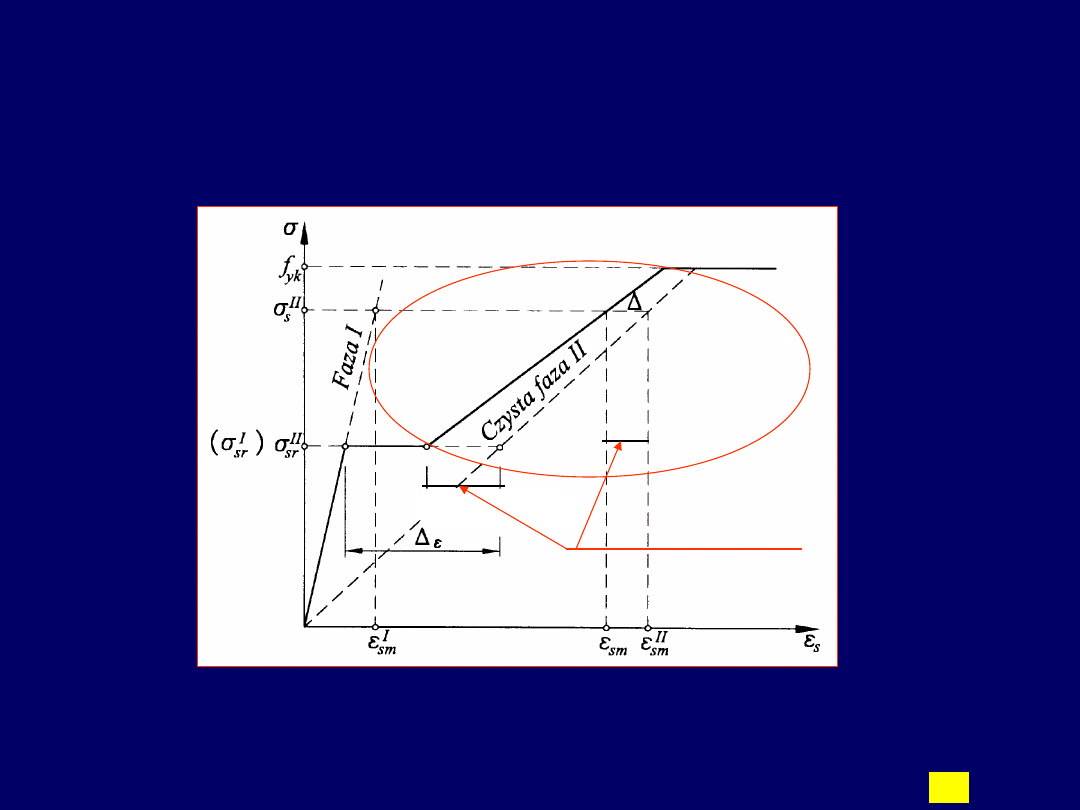
Interpretacja graficzna do wyznaczenia 

średnich odkształceń zbrojenia – z 

uwzględnieniem efektu „tension stiffening”

                 

Δε

sm

Do chwili zarysowania przekroju naprężenia i odkształcenia w zbrojeniu opisane są linią prostą
 (faza I). Po osiągnięciu obciążenia rysującego (momentu lub siły), dochodzi do powstania rysy,
 a odkształcenia w zbrojeniu (w przekroju przez rysę) wzrastają skokowo o wartość  





Obszar 
wystąpien
ia
efektu 
„tension 
stiffening
” 

efekt „tension stiffening”



 

 

28

Różnica odkształceń w zbrojeniu i betonie zapisuje się wzorem

s

s

s

eff

p,

e

eff

p,

eff

ct,

1

s

cm

sm

E

σ

 

0,6

  

    

E

)

ρ

α

(1

 

ρ

f

k

 -

 

σ

  

  

ε

  

- 

ε







Obliczenie szerokości rysy wg 

Eurokodu 2











 



3

1

II

s

Ed

s

x

d

A

M



gdzie

 

 

29

gdzie-                   -naprężenie w stali rozciąganej w stanie zarysowania. 

e



s



Iloraz E

s 

/ E

cm

Efektywny stopień zbrojenia,

s

s

s

eff

p,

e

eff

p,

eff

ct,

1

s

cm

sm

E

σ

 

0,6

  

    

E

)

ρ

α

(1

 

ρ

f

k

 -

 

σ

  

  

ε

  

- 

ε







ef

c

s

ef

p

A

A

,

,





ef

c

A

,

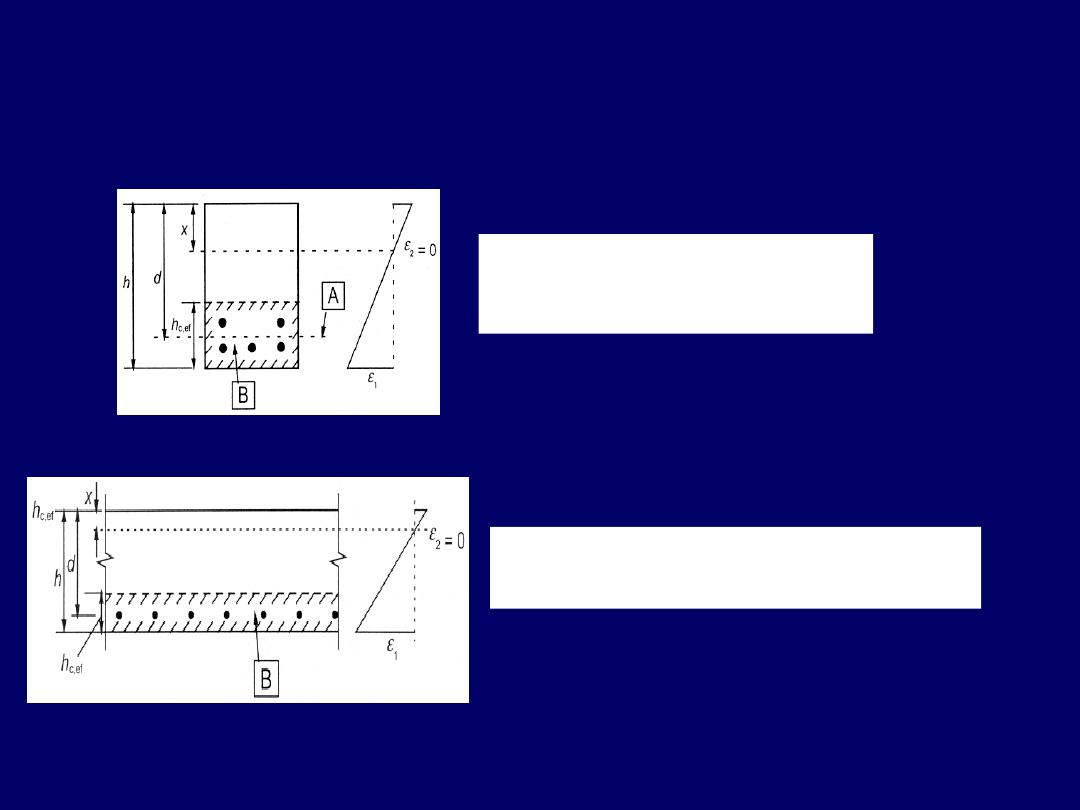
Efektywne pole strefy rozciąganej o wysokości h

c,ef  

(patrz rysunek)

1

k

Parametr uwzględniający czas działania obciążenia

k

1

 =

 

0,6  -obciążenia krótkotrwałe,

k

1

 = 

0,4 –obciążenia długotrwałe

 

 

30

Efektywna strefa rozciągana (przypadki typowe) 

A

ct,eff

A  -poziom środka ciężkości 
zbrojenia

B   - efektywna strefa rozciągana 
A

c,ef

B   - efektywna strefa rozciągana A

c,ef

Belka

Płyta

 

 

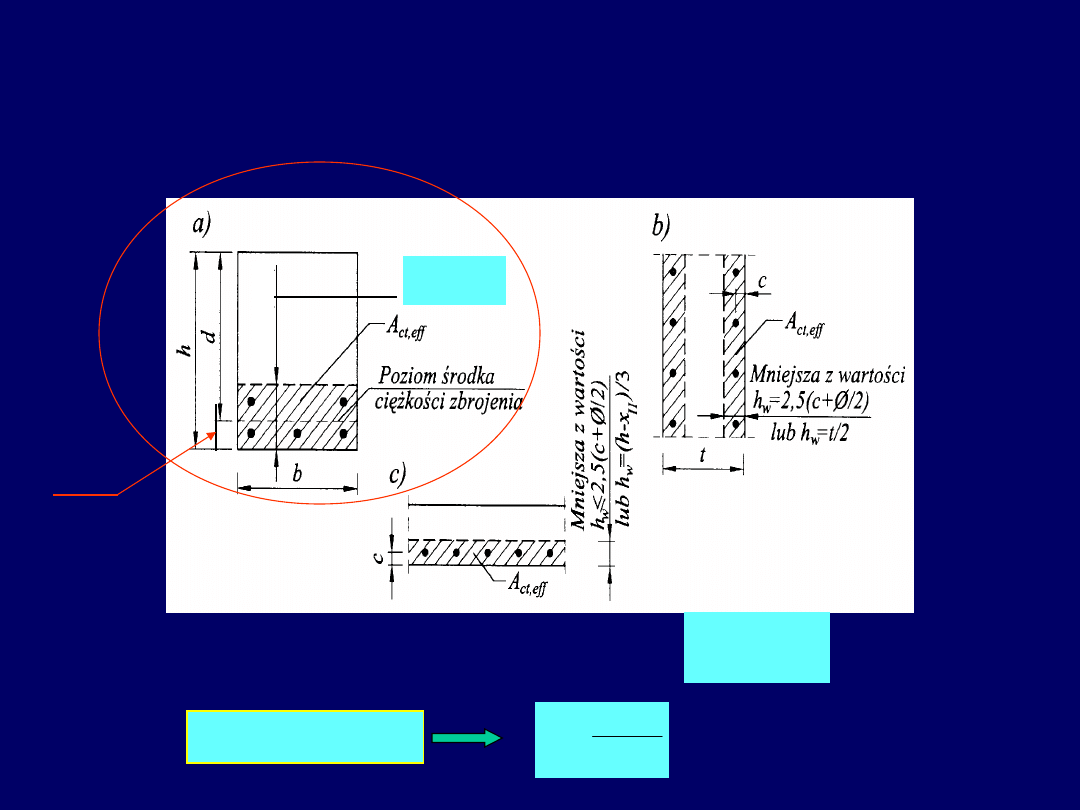
31

Ustalanie stopnia zbrojenia rozciąganego na 

powierzchni przekroju efektywnej strefy rozciąganej 

A

ct,ef



















3

/

5

,

2

min

II

x

h

d

h



















3

/

5

,

2

min

II

x

h

d

h

Przyjmujemy wartość h

w

 mniejszą z dwu wartości

 

a

1

A

ct,eff 

=  h

w 

x b

w

ef

ct

s

r

A

A

,





 

 

32

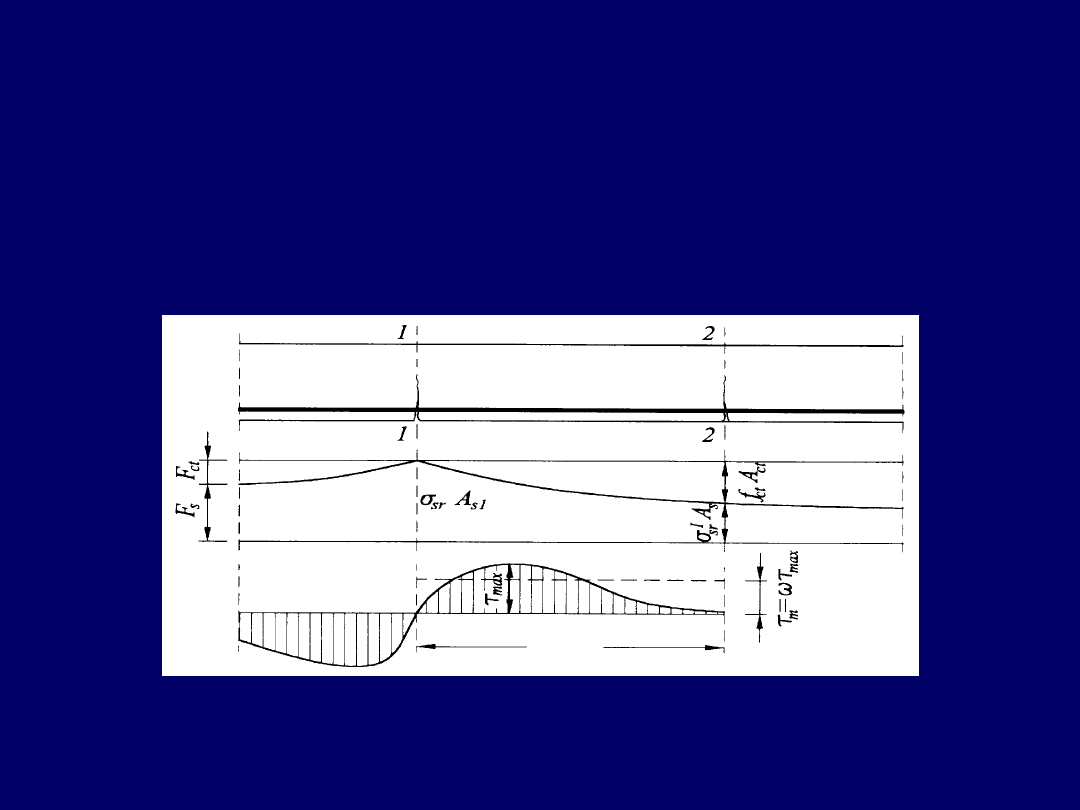
Wykres naprężeń w zbrojeniu i betonie w otoczeniu rysy na odcinku s

r

:

a)      naprężenia rozciągające, b) naprężenia przyczepności

Długość rozstawu rys s

r

Przyrostowi naprężeń w prętach zbrojenia w przekroju 1-1 (przez rysę) towarzyszy 
wzrost naprężeń przyczepności w pręcie na odcinku o nieznanej długości s

r

. 

Długość tego odcinka (rozstawu rys wyznacza się na podstawie 
wykresu naprężeń rozciągających w zbrojeniu na długości elementu 
(w otoczeniu rysy) oraz wykresu naprężeń przyczepności betonu do zbrojenia.  

S

r,max

 

 

33

Maksymalny końcowy rozstaw rys

wher
e

*

s





Średnica pręta

Otulina zbrojenia podłużnego

c

1

k

Współczynnik uwzględniający przyczepność zbrojenia: 

s

r,max

  =  k

3

c  +  k

1

k

2

k

4 

 / 



p,ef

  

8

,

0

1



k

Pręty żebrowane

6

,

1

1



k

Pręty gładkie

2

k

Współczynnik uwzględniający kształt wykresu naprężeń

5

,

0

2



k

Zginanie

0

,

1

2



k

Czyste rozciąganie

4

,

3

3



k

425

,

0

4



k

 

 

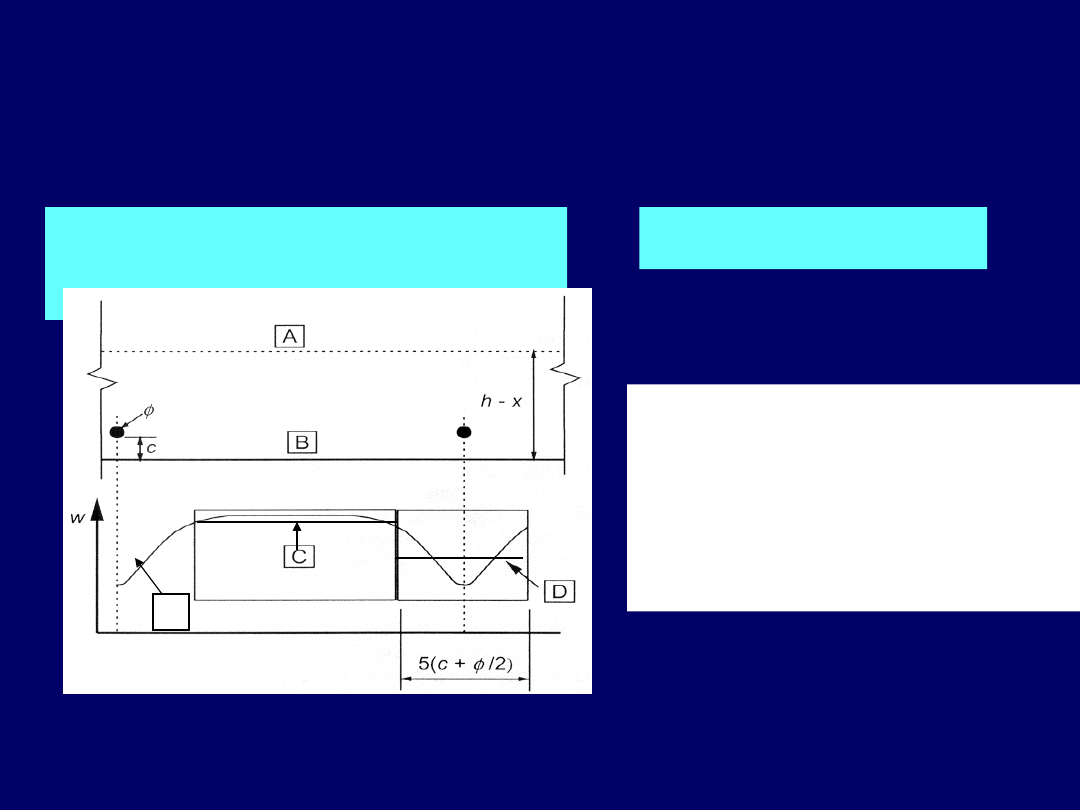
34

s

r,max

  =  k

3

c  +  k

1

k

2

 k

4 

 / 



p,ef

  

A  -  Oś obojętna
B  -  Powierzchnia betonu
C  -  Odległość pomiędzy prętami ze 
wzoru
        uproszczonego
D  - Odległość pomiędzy prętami ze 
wzoru
        dokładnego 
E  – Aktualna szerokość rysy

E

Wzór dokładny

s

r,max

  = 1,3 (h – x)

Wzór uproszczony

Gdy odległość prętów przekracza 5 (c + φ/2 )

Maksymalny końcowy rozstaw rys

 

 

35

Określanie minimalnego zbrojenia z uwagi 

na zarysowanie 

Minimalne pole przekroju zbrojenia na zarysowanie pod wpływem obciążeń pośrednich
(np. od temperatury) obliczamy ze wzoru

s

ct

ef

ct

c

s

A

f

kk

A



,

min

,



k

c

 - ws

spółczynnik uwzględniający kształt wykresu naprężeń w strefie rozciąganej w 

chwili 
       powstania rysy, przyjmowany jak niżej:
     -  przy rozciąganiu osiowym (prostokątny kształt wykresu) k

c

 = 1,0,

     -  przy zginaniu k

c

 = 0,4.

k - współczynnik korekcyjny, w ogólnym przypadku przyjmowany jako równy:

-  przy naprężeniach wymuszonych przyczynami zewnętrznymi: k = 1,0

-- przy naprężeniach wymuszonych przyczynami wewnętrznymi 

-- przy wysokości h  300 mm        k = 1,0,

-- przy wysokości h  800 mm        k = 0,65.

ctm

ef

ct

f

f



,

 

 

36

Dziękuję za uwagę