Maciej Chmielowski gr22 z8.

Laboratorium Fizyki

Ćw. 12 Badanie procesów relaksacyjnych w obwodach elektrycznych.

1. Wstęp

Proces relaksacyjny może być określony jako przejście układu makroskopowego do stanu równowagi (minimalnego potencjału termodynamicznego). Polega na rozproszeniu energii. Procesy relaksacyjne charakteryzują się tym, że szybkość przebiegu procesu jest proporcjonalna do wartości odchylenia wielkości mierzonej od równowagii w danej chwili. Procesy relaksacyjne matematycznie opisywane są przez malejące funkcje wykładnicze, w przypadku rozpraszania energii, i rosnące, w przypadku lokalnego gromadzenia jej. Ważnym współczynnikiem jest τ, czas relaksacji. Jest to czas, po którym obserwowana wielkość ulegnie e-krotnej zmianie. Procesy gromadzenia i rozpraszania energii mogą przebiegać naprzemiennie, jeśli przy przekazywaniu energii z otoczenia układ osiąga stan równowagi nietrwałej. Wtedy układ może rozproszyć zgromadzoną energię wielokrotnie szybciej niż jest mu przekazywana. Jeśli energia jest dostarczana do układu ciągle, to gromadzenie i rozpraszanie jej będzie następowało okresowo, powstaną drgania relaksacyjne.

W tym ćwiczeniu zajmujemy się drganiami relaksacyjnymi w układzie RC, z dostawioną lampą neonową, kluczującą czyli zwierającą i rozwierającą obwód w zależności od napięcia na jej zaciskach. Najpierw w czasie ładowania kondensatora, układ jest rozwarty (lampa rozwiera obwód przez za niskie napięcie) rośnie napięcie na zaciskach lampy. Następnie, gdy napięcie osiągnie napięcie zapłonu lampy, następuje gwałtowny przepływ ładunku przez lampę, rozładowanie kondensatora, i spadek napięcia do napięcia gaśnięcia lampy, kiedy to przerywa ona obwód. Proces ten ma charakterystykę drgań relaksacyjnych.

2. Układ pomiarowy.

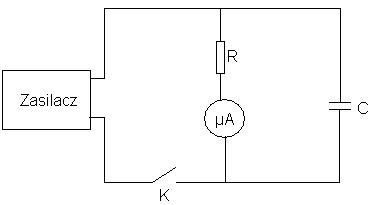
I. Badanie procesu rozładowania kondensatora.

R- opornik o rezystancji 200 lub 300kΩ; C- kondensator 100μF; μA- mikro amperomierz klasy 0,2 o zakresie 150μA; K-klucz pozwalający na zwieranie i rozwieranie układu

Układ składa się z zasilacza, mikroamperomierza, opornika, kondensatora, klucza. Klucz pozostawiamy rozwarty, w celu naładowania kondensatora, a po krótkim czasie zwieramy go, by obserwować przepływ prądu (natężenie) w czasie rozładowywania kondensatora. Użyto oporników o rezystancjach 200 i 300kΩ.

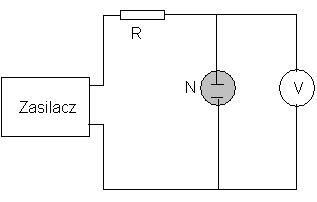
II. Pomiar napięcia zapłonu Uz i gaśnięcia Ug neonówki.

R- opornik; N- neonówka; V- woltomierz cyfrowy V530 c1=0,05% c2=0,01%

Układ składa się z zasilacza, opornika, neonówki i woltomierza. Napięcie na zaciskach zasilacza reguluje się tak, by dojżeć napięcie tuż przed zapłonem neonówki (Uz), i następnie obniża się je, by dojżeć napięcie gaśnięcia (Ug).

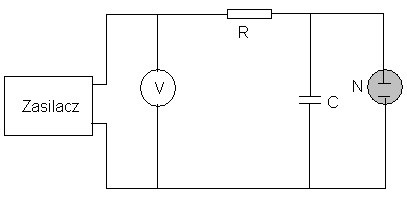
III. Badanie zależności okresu drgań od wartości rezystancji R i pojemności C.

R- opornik; N- neonówka; V- woltomierz cyfrowy V530 c1=0,05% c2=0,01%; C- kondensator Układ składa się z woltomierza, oporników o rezystancjach od 300 do 825kΩ, kondensatorow o pojemnościach 2,2 1 i 0,47μF i neonówki. Przy ustalonym napięciu zasilacza kolejno zmienia się oporniki 300, 360, 430, 510, 620, 750, 825kΩ. Po takim cyklu zmienia się kondensator na pojemność mniejszą (zaczynając od 2,2μF, kończąc na 0,47μF) 3. Wykonanie ćwiczenia

ćwiczenie składało się z 3 części:

I. Badanie procesu rozładowania kondensatora

1. Zestawić układ pomiarowy według schematu

2. Włączyć zasilanie

3. Odczekać aż kondensator naładuje się.

4. Za pomocą klucza K zamknąć obwód

5. Co pięć sekund odczytywać wartość natężenia prądu i zapisywać ją. Zapisać także czas połowicznego spadku natężenia prądu.

6. Przerwać pomiary gdy natężenie zejdzie do 5% wartości początkowej.

7. Wykonać pomiary dla oporu 300 i 200kΩ

II. Pomiar napięcia zapłonu Uz i gaśnięcia Ug neonówki.

1. Zestawić układ pomiarowy

2. Przez obrót pokrętła zasilacza powoli zwiększać napięcie aż zapali się neonówka

3. Zapisać najwyższą wartość napięcia przed zapaleniem neonówki (Uz) 4. Powoli obniżać napięcie i zanotować wartość przy której gaśnie neonówka (Ug).

5. Powtórzyc dziesięciokrotnie.

III. Badanie zależności okresu drgań od wartości rezystancji R i pojemności C.

1. Zestwić układ pomiarowy.

2. Ustawić takie napięcie zasilacza, by neonówka blyskała.

3. Zmierzyć czas 10 rozbłysków neonówki dla różnych R (od 300 do 825kΩ) 4. Wykonać pomiary dla pojemności kondensatora równych 2,2 1 i 0,47μF.

5. Oszacować niepewności R, C, Uz, Ug, U.

4. Wyniki i ich opracowanie

I . Badanie procesu rozładowania kondensatora

R [kΩ]

t[s]

0

5

10

15

20

25

30

35

40

45

50

55

60

65

70

R =300

1

I[μA] 150

125

105

87

75

64

54

45

37

32

27

23

20

16

14

C =100μF

1

R =200

I[μA]

2

150

114

89

68

54

41

32

25

19

15

12

--

--

--

--

Czas połowicznego zaniku prądu (spadku natężenia do połowy pierwotnej wartości) wyniósł: T1/2=(18±1,1)s dla R=300kΩ

T1/2=(12±1,1)s dla R=200kΩ

Rachunek błędów:

Niepewność eksperymentatora przy pomiarze czasu:

1s

u(t)=

=0,57

3

U(t)=0,57*2=1,14

Wykres wykonany w programie Origin załączony do sprawozdania.

Dla R=300kΩ:

1

1

1/czas relaksacji =

= =− slope=0,0345

czas relaksacji 

τ = (28,9855072±0,0000006)s

Test Chi kwadrat:

Dla tego wykresu, χ2=53, natomiast χ2kryt dla 15 pomiarów, czyli 13 stopni swobody jest χ2kryt=22,4. Należy więc odrzucić hipotezę o liniowości zależności.

Dla R=300kΩ:

1

1

1/czas relaksacji =

= =− slope=0,05172

czas relaksacji 

τ = (19,3348801±0,00000002)s

Dla tego wykresu, χ2=102, natomiast χ2kryt dla 9 pomiarów, czyli 7 stopni swobody jest χ2kryt=14,1. Należy więc odrzucić hipotezę o liniowości zależności.

Rachunek błędów:

1 2

1

u =  ∗ u  =0,0000003 dla=20 i 0,0000001 dla =33

Niepewność złożona:





U(τ)=0,0000006s dla τ=20s

U(τ)=0,0000002s dla τ=33s

Obliczenia na podstawie znajomości pojemności i rezystancji: τ=R*C

τ=300Ω*100F*10-6*103=(30±3)s

τ=200kΩ*100μF=(20±2)s

Rachunek błędów:

u(C)=x*5%=5μF

u(R)=x*0,5%=1,5 lub 1kΩ

ponieważ τ=R*C

u  τ = R 2∗ u 2 C  C 2∗ u 2 R

dla R=300kΩ

u(τ)=1,51s

U(τ)=3s

dla R=200kΩ

u(τ)=1s

U(τ)=2s

Informacje odczytane z wykresu:

τ=(20,0±6,8)s

τ=(29,0±6,8)s

Rachunek błędów:

Niepewność eksperymentatora przy odczytywaniu danych z wykresu: (błąd odczytu każdej wielkości szacuję na 2)

u  I =22=2,4

3

u  t=22=2,4

3

Wynika z tego, niepewność τ z wykresu:

u  τ = u 2 τ  u 2 I = 2,422,42=3,39

U(τ)=6,78

II . Pomiar napięcia zapłonu Uz i gaśnięcia Ug neonówki.

1

2

3

4

5

6

7

8

9

10

U [V]

z

72,0 71,5

70,5

71,5 72,2 71,6 71,8 70,1 72,6 71,9

U [V]

g

56,0 56,7

56,8

56,5 56,4 56,7 56,2 56,5 56,4 56,4

Wyniki pomiaru:

Uz= (71,6±1,5)V

Ug= (56,49±0,48)V

Rachunek błędów:

Średnie Uz= 71,57V

Średnie Ug= 56,46V

u(Uz)= 0,75V (odchylenie standardowe)

∆x=c1*x + c2*z=71,5V*0,05% + 100V*0,01% =0,026V (niepewność wzorcowania, pomijalnie mała)

U(Uz)=2*0,75=1,5V (niepewność rozszerzona pomiaru napięcia zapłonu) u(Ug)= 0,24V (odchylenie standardowe)

∆x=0,026V (niepewność wzorcowania, z tego samego urządzenia co Uz) U(Ug)=2*0,24=0,48V (niepewność rozszerzona pomiaru napięcia gaśnięcia) III . Badanie zależności okresu drgań od wartości rezystancji R i pojemności C.

Wyniki pomiaru:

C[μF]

U [V] R [kΩ]

t[s]

C[μF]

U [V] R [kΩ]

t[s]

C[μF]

U [V] R [kΩ]

t[s]

825

20,7

825

9,2

825

4,8

750

18,3

750

8,0

750

4,3

620

15,6

620

7,0

620

3,9

2,2

80,5

510

12,9

1

80,5

510

6,4

0,47

80,5

510

3,7

430

11,0

430

5,4

430

3,2

360

9,1

360

4,6

360

3,1

300

8,6

300

3,8

300

3,0

Na podstawie wyników obliczono niepewności pomiaru okresu drgań relaksacyjnych T: T=t1 + t2 = czas ładowania kondensatora + czas rozładowania kondensatora. Jednakże, t2 jest wielokrotnie mniejsze od czasu ładowania, więc można je pominąć w obliczeniach.

Czas ładowania wyraża się wzorem:

− U

t = R∗ C∗ln 

g 

1

− U z

R- rezystancja opornika, C- pojemność kondensatora, Ug- napięcie gaśnięcia neonówki, Uz- napięcie zapłonu neonówki, ε- napięcie na zaciskach zasilacza.

Tak więc, przyjmujemy, że T=t1.

By obliczyć niepewność pomiaru T, trzeba obliczyć pochodne po wszystkich zmiennych we wzorze:

− U

T ' = C∗ln

g 

R

− U z

− U

T ' = R∗ln 

g 

C

− U z

RC

T ' =

Ug

− U g

RC

T ' =

Uz

− U z

U − U

T ' =

g

z



− U g − U z

Więc u(T) wyraża się wzorem:

u  T = T ' 2∗ u 2 R T ' 2∗ u 2 C  T ' 2∗ u 2  U  T ' 2∗ u 2 U  T ' 2∗ u 2

R

C

Ug

g

Uz

z



Po podstawieniu stosownych wartości otrzymujemy:

U= napięcie na zaciskach zasilacza,

t =czas 10 błyśnięć lampy

R=rezystancja opornika

C=pojemność kondensatora

Teksp=okres na podstawie eksperymentu(czas n błyśnięć/n)

Tobl= okres obliczony ze wzoru

u( Tobl)= niepewność złożona pomiaru na podstawie obliczeń u(Teksp)=niepewność złożona na podstawie eksperymentu

U

t[s]

R [kΩ] C[μF] T

[s] T [s]

u(T )[s] u(T ) [s]

eksp

obl

ek

obl

80,5

20,7

825

2,2

2,07

1,80

0,057

0,200

80,5

18,3

750

2,2

1,83

1,64

0,057

0,182

80,5

15,6

620

2,2

1,56

1,35

0,057

0,150

80,5

12,9

510

2,2

1,29

1,11

0,057

0,124

80,5

11,0

430

2,2

1,10

0,94

0,057

0,104

80,5

9,1

360

2,2

0,91

0,79

0,057

0,087

80,5

8,6

300

2,2

0,86

0,65

0,057

0,073

80,5

9,2

825

1

0,92

0,82

0,057

0,091

80,5

8,0

750

1

0,80

0,74

0,057

0,083

80,5

7,0

620

1

0,70

0,62

0,057

0,068

80,5

6,4

510

1

0,64

0,51

0,057

0,056

80,5

5,4

430

1

0,54

0,43

0,057

0,047

80,5

4,6

360

1

0,46

0,36

0,057

0,040

80,5

3,8

300

1

0,38

0,30

0,057

0,033

80,5

4,8

825

0,47

0,48

0,38

0,057

0,043

80,5

4,3

750

0,47

0,43

0,35

0,057

0,039

80,5

3,9

620

0,47

0,39

0,29

0,057

0,032

80,5

3,7

510

0,47

0,37

0,24

0,057

0,027

80,5

3,2

430

0,47

0,32

0,20

0,057

0,023

80,5

3,1

360

0,47

0,31

0,17

0,057

0,019

80,5

3,0

300

0,47

0,30

0,14

0,057

0,016

Wykresy obrazujące zależności T od R, dla stałych pojemności kondensatora równych 2,2, 1 lub 0,47:

Obliczeniowe:

900

800

700

600

500

2,2

R

1

400

0,47

300

200

100

0

0,00 0,20 0,40 0,60 0,80 1,00 1,20 1,40 1,60 1,80 2,00

T

Eksperymentalne:

900

800

700

600

500

R

2,2

400

1

0,47

300

200

100

0

0,20 0,40 0,60 0,80 1,00 1,20 1,40 1,60 1,80 2,00 2,20

T

5. Wnioski

Zadziwiające w tym ćwiczeniu okazały się wartości chi kwadrat obliczone przez program origin. Znacząco przekroczyły wartości chi kwadrat krytycznej, przez co zdaje się, że nie ma nawet cienia szansy, by zależność przez nas badana była prawdziwa. Jednakże, wiemy, iż zależność ta jest logarytmiczna, więc prawdopodobnie błędy pomiaru spowodowały taką wysoką wartość chi kwadrat. Możliwe, że przy pomiarach napięcia zapłonu i gaśnięcia neonówki, błędy pomiaru były większe niż wynikające z parametrów urządzenia, poniważ mierzono wielkość stale się zmieniajacą, więc powinno się wziąć pod uwagę refleks badacza. Takie same błędy (i to właśnie w części ćwiczenia badanej przez chi kwadrat) mogły mieć miejsce przy pomiarze prądu rozładowania kondensatora. Pomiar natężenia prądu w odstępach pięcio-sekundowych z pewnością miał mniejszą dokładność niż wynikająca z parametrów urządzenia (w tym typu B), ponieważ, chociażby w początkowych częściach pomiaru, wartośc zmieniała się gwałtownie. Pomiaru nie ułatwił też mechanizm wskazań urządzenia, nie poprzez wskazówkę, a punkt światła, o dużej średnicy względem działki. Pomiar także był wykonywany przez dwie osoby, jedną mierzącą czas, a drugą zapisującą natężenie prądu, przez co opóźnienia w komunikacji mogły znacząco zwiększyć błąd pomiaru.

Widać, że błędy przyjęte przez progam są o kilka rzędów wielkości mniejsze, niż wynikające z obliczeń przy użyciu niepewności złożonej dla czasu relaksacji.

Przy tak dużych błędach pomiaru, względem niepewności złożonych a nawet i rozszerzonych, niemożliwe było uznanie hipotezy za słuszną, mimo, że tak na prawdę jest.

Pozostała część ćwiczenia dotyczyła wyznaczania okresu drgań relaksacyjnych. Tu także można było popełnić znaczne błędy, chociażby przy mierzeniu okresu drgań relaksacyjnych. Nawet dziesięć okresów było już na granicy możliwości ludzkiej do zmierzenia. Dla tego też, niepewność okresu obliczonego, a nie zmierzonego, jest mniejsza od niepewności okresu zmierzonego.

Podsumowując, największą bolączką eksperymentatora w tym ćwiczeniu były jego własne błędy.