ZESTAW ALG2S

1. liczby 43 i -93, zamienić na:

• U2

• ósemkowy, szestnastkowy

• dodać binarne te dwie liczby

• wynik przeliczyć na dziesiętny

(10)

2. Udowodnić tożsamość

abcd + a + b + c + d + d ( a + b + c) + b( a + c + d ) = a + c (8)

3. Dane są 2 liczby 2 bitowe A (a1 i a2) i B (b1 i b2), znaleźć minimalne równanie funkcji F

przyjmującej wartość „prawda” w przypadku gdy liczba AB wynosi 2.

(6)

4. Dana jest funkcja F(a,b,c,d)=(0, 1, 2, 6, 8, 10, 11, 14) Korzystając z tablicy Karnough przekształcić ją do postaci pozwalającej na realizację układową tej funkcji wykorzystującej bramki NAND.

ab\cd

00 01 11 10

00

01

11

10

(6)

5. Dana jest funkcja logiczna G (x0,x1,x2,x3) zapisana w poniżej w tabeli Karough – zapisać w minimalnej postaci.

(tabeli nie zapisałem ale chyba wiadomo ocb :) ) (6)

6. Przekształcić do postaci finkcji wielomianowej funkcję F, oraz sprawdzić, czy funkcja jest funkcją liniową, zachowującą zera i zachowującą 1.

F(a,b,c)=abc+ab

(8)

7. Tabela wzbudzeń i warunki sterowania przerzutników D i JK.

(6)

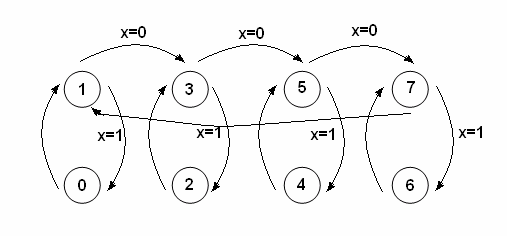
8. Zaprojektować licznik synchroniczny wyposażony w wejście sterujące x realizujący następujący diagram stanów . Do budowy licznika należy wykorzystać przerzutniki typu D.

Należy skonstruować tablice przejść przerzutników , tablica Karnough dla wejść przygotowujących, napisać funkcje logiczne dla wejść przygotowujących.

(10)

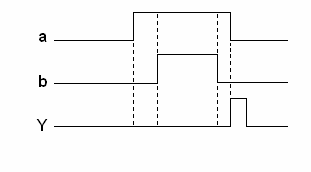
9. Zaprojektować układ synchroniczny na przerzutnikach typu JD wykonujący sekwencję sygnałów a i przedstawiony na rysunku:

Wykrycie sekwencji ma być sygnalizowane na wyjściu Y układu impulsem o wartości 1

trwającym 1 okres zegara. należy podać diagram stanów, tablicę przejść tablicę Karnough dla wejść przerzutników i napisać funkcje logiczne dla wejść przygotowujących.

(10)