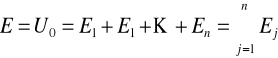
Łączenie szeregowe i równoległe źródeł napięcia

1. Łączenie szeregowe.

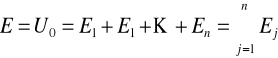
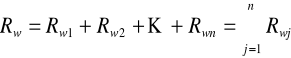
Układ szeregowy n gałęzi aktywnych i pasywnych (E_j= 0) można zastąpić jedną gałęzią aktywną o napięciu źródłowym E równym sumie napięć źródłowych i o rezystancji R_w równej sumie rezystancji poszczególnych gałęzi aktywnych i pasywnych.

2. Łączenie równoległe.

Układ równoległy n gałęzi aktywnych o dowolnych napięciach źródłowych E_j i konduktancjach G_j , można zastąpić jedną gałęzią o napięciu źródłowym równym sumie iloczynów konduktancji i napięć źródłowych poszczególnych gałęzi podzielonej przez sumę ich konduktancji, która jest zarazem konduktancją gałęzi zastępczej.

Rezystancja gałęzi zastępczej:

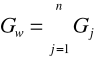
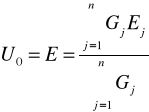
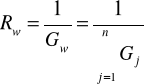
Prawa Kirchhoffa

I Prawo Kirchhoffa (prądowe) - suma prądów wpływających do węzła jest równa sumie prądów odpływających od węzła.

Σ I = 0

Suma algebraiczna prądów dopływających i odpływających z dowolnie wydzielonego fragmentu obwodu elektrycznego jest równa zeru.

II Prawo Kirchhoffa (napięciowe) - Suma napięć źródłowych w dowolnym oczku obwodu elektrycznego prądu stałego jest równa sumie iloczynów rezystancji i prądów w gałęziach należących do danego oczka.

U_ab = V_a - V_b = E₁ - R₁I₁

U_bc = V_b - V_c = E2 - R₂I₂

U_cd = V_c - V_d = -E₃ +R₃I₃

U_da = V_d - V_a = R₄I₄

E₁ - R₁I₁ +E₂ - R₂I₂ - E₃ + R₃I₃ +R₄I₄ = 0

lub

R₁I₁ +R₂I₂ - R₃I₃ - R₄I₄ = E₁+E₂ - E₃

Σ (RI) = Σ E

Σ (E,U) = 0

W dowolnym oczku obwodu elektrycznego prądu stałego suma algebraiczna napięć źródłowych i napięć odbiornikowych jest równa zeru (jeżeli obwód nie jest poddany działaniu zmiennych pól elektromagnetycznych).

Zastosowanie praw Kirchhoffa do rozwiązywania obwodów elektrycznych rozgałęzionych

Rozwiązywanie obwodu elektrycznego polega na wyznaczaniu prądów przy danych parametrach obwodu i działających w nim wymuszeniach.

Liczba niewiadomych równań jest równa liczbie gałęzi g. Dla ich wyznaczania służą równania prądowe wg I prawa Kirchhoffa dla węzłów

Σ I_k = 0

oraz równania napięciowe wg II prawa Kirchhoffa dla oczek

Σ ( R_k I_k ) = Σ E_k

Liczba równań prądowych w obwodzie o w węzłach wynosi (w-1)

Brakujące równania w liczbie n = g - ( w - 1 ) = g - w +1 należy wypisać na podstawie II prawa Kirchhoffa, gdzie n oznacza liczbę niezależnych oczek w danym obwodzie.

Po wypisaniu równania dla dowolnego oczka skreśla się w nim jedną gałąź w tym celu, aby ją ominąć przy doborze następnych oczek. Postępowanie jest zakończone, gdy nie można utworzyć oczka z samych nie skreślonych oczek.

Metoda oczkowa rozwiązywania obwodów elektrycznych

Liczba niezależnych równań Kirchhoffa, stanowiących podstawę analizy obwodu elektrycznego, jest równa liczbie gałęzi g w danym obwodzie. Składają się na nie równania prądowe w liczbie (w-1) i równania napięciowe w liczbie n oznaczającej liczbę niezależnych oczek.

Metoda oczkowa może być stosowana do rozwiązywania obwodów spełniających zasadę superpozycji, a więc obwodów liniowych.

R₁₁I₁ + R₁₂I₂ + R₁₃I₃ + ... + R_1nI_n = (ΣE)₁

R₂₁I₁ + R₂₂I₂ + R₂₃I₃ + ... + R_2nI_n = (ΣE)₂

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

R_n1I₁ + R_n2I₂ + R_n3I₃ + ... + R_nnI_n = (ΣE)_n

(ΣE)_j - suma napięć źródłowych w oczku j.

Rezystancje własne oczek zawsze ze znakiem (+).

Rezystancje wzajemne ze znakiem (+) jeżeli zwroty prądów oczkowych są zgodne, ze znakiem (-) gdy zwroty prądów oczkowych są przeciwne.

Jeżeli w obwodzie istnieją źródła prądu należy je najpierw zamienić na źródła napięcia, lub tak dobierać oczka, aby znany prąd źródłowy był jednocześnie prądem oczkowym i gałęziowym.

Metoda potencjałów węzłowych

Prąd w gałęzi aktywnej o danych parametrach E oraz G lub R jest zależny od potencjałów na końcach gałęzi.

I_k1 = G(V_k - V₁) + GE

W przypadku gałęzi pasywnej E=0 czyli I_k1 = G(V_k - V₁)

Prąd w dowolnej gałęzi obwodu elektrycznego prądu stałego można wyrazić za pomocą parametrów E, G tej gałęzi oraz różnicy potencjałów na końcach gałęzi, tj. potencjałów węzłowych.

Bilans prądów w węźle l przy przyjętych zwrotach:

I_1l + I₂₁ + I_2l + I_kl = 0

Prądy w poszczególnych gałęzniach:

I_1l = G_1l (V₁ - V₂) + G_1l E_1l

I_2l = G_2l (V₂ - V₁) + G_2l E_2l

I_3l = G_3l (V₃ - V₁) + G_3l E_3l

I_kl = G_kl (V_k - V₁)

Po przekształceniach otrzymujemy równanie dla węzła l:

(G_1l + G_2l + G_3l + G_kl)V_l - (G_1l V₁ + G_2l V₂ + G_3l V₃ + G_kl V_k) = G_1l E_1l - G_2l E_2l + G_3l E_3l

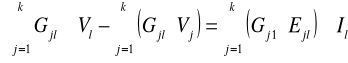
Ogólnie (równanie węzłowe):

Iloczyn sumy konduktancji łączących rozpatrywany węzeł l z węzłami sąsiednimi, przez potencjał tego węzła V_l, pomniejszony o sumę iloczynów konduktancji tych gałęzi G_jl i potencjałów V_j węzłów sąsiednich jest równy sumie iloczynów tych konduktancji i napięć źródłowych E_jl w wymienionych gałęziach.

Napięciom źródłowym E_jl skierowanym do rozpatrywanego węzła przypisujemy znak (+), a znak (-) skierowanym przeciwnie.

Jeżeli do węzła l dopływa prąd I_l to należy go dodać do prawej strony równania węzłowego ze znakiem (+) jeżeli dopływa, ze znakiem (-) gdy wypływa.

Równania węzłowe przyjmują następującą postać ogólną :

G_1l V₁ - G₁₂ V₂ - G₁₃ V₃ ... - G_1m V_m = (ΣI_źr)₁

G_2l V₁ - G₂₂ V₂ - G₂₃ V₃ ... - G_2m V_m = (ΣI_źr)₂

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

G_ml V₁ - G_m2 V₂ - G_m3 V₃ ... - G_mm V_m = (ΣI_źr)_m

Konduktancje własne węzłów występują ze znakiem (+), a konduktancje wzajemne węzłów ze znakiem (-). Gdy węzły nie są połączone ich wzajemna konduktancja wynosi 0.

Twierdzenie o kompensacji

Punkty ekwipotencjalne w obwodzie elektrycznym można ze sobą zewrzeć nie powodując przez to zmian w rozpływie prądów.

Twierdzenie o kompensacji: Rozpływ prądów w obwodzie elektrycznym nie ulegnie zmianie, jeżeli dowolny element rezystancyjny R tego obwodu zostanie zastąpiony źródłem idealnym o napięciu źródłowym R równym spadkowi napięcia RI na tym elemencie i o zwrocie przeciwnym niż zwrot prądu I.

Napięcie źródłowe, którego wartość i zwrot zależą od prądu płynącego przez źródło nazywa się napięciem źródłowym sterowanym.

Napięcie źródłowe, którego wartość i zwrot nie zależą od prądu płynącego przez źródło nazywa się napięciem źródłowym niesterowanym.

Element rezystancyjny R, przez który płynie prąd I, można zastąpić idealnym źródłem napięcia o napięciu źródłowym sterowanym: E = RI.

Rozwiązywanie obwodów elektrycznych metodą superpozycji

Prąd w dowolnie wybranej gałęzi k przy jednoczesnym działaniu wielu idealnych źródeł napięcia w obwodzie

I_k = I_k1 + I_k2 + ... + I_kg

jest sumą algebraiczną prądów wywołanych w tej gałęzi przez poszczególne źródła napięcia.

Potencjał w dowolnym węźle obwodu liniowego zasilanego przez wiele źródeł napięcia i prądu jest sumą potencjałów wywołanych w tym węźle przez poszczególne źródła przy przyjęciu, że potencjał jednego z węzłów ma stale tą samą wartość, np. równą zeru w wyniku uziemienia.

Metodę superpozycji można stosować do rozwiązywania obwodów elektrycznych. W tym celu oblicza się prądy w gałęziach lub potencjały węzłów, pochodzące od poszczególnych źródeł zakładając, że wszystkie inne źródła mają napięcia źródłowe i prądy źródłowe równe zeru, ale ich rezystancje wewnętrzne i bocznikujące pozostają w obwodzie. Otrzymane wyniki dodaje się algebraicznie.

Twierdzenie Thevenina i Nortona

a. Twierdzenie Thevenina.

Prąd płynący przez odbiornik rezystancyjny R, przyłączony do dwóch zacisków a - b dowolnego liniowego układu zasilającego prądu stałego jest równy ilorazowi napięcia U₀ mierzonego na zaciskach a - b w stanie jałowym przez rezystancję R powiększoną o rezystancję zastępczą R_w układu zasilającego mierzoną na zaciskach a - b.

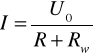
lub

Obwód elektryczny liniowy o dowolnym ukształtowaniu, traktowany jako złożony dwójnik liniowy aktywny o zaciskach a - b, można zastąpić jednym źródłem o napięciu źródłowym E, równym napięciu stanu jałowego U₀ na zaciskach a - b i o rezystancji zastępczej mierzonej na zaciskach a - b obwodu.

Rezystancję R_w można wyznaczyć z pomiaru stanu zwarcia na zaciskach a - b.

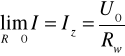
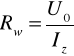
stąd

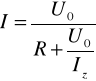
Do scharakteryzowania aktywnego dwójnika liniowego prądu stałego wystarcza znajomość napięcia stanu jałowego i prądu zwarcia.

3. Twierdzenie Nortona.

Każdy liniowy obwód elektryczny prądu stałego, traktowany jako dwójnik źródłowy o zaciskach a - b, można zastąpić jednym źródłem prądu o prądzie I_żr = U₀/R_w = I_z , równym prądowi zwarcia na zaciskach a - b oraz równolegle włączonym opornikiem o konduktancji G_w = 1/R_w równej konduktancji wewnętrznej obwodu mierzonej na zaciskach a - b.

Prąd płynący przez odbiornik jest proporcjonalny do konduktancji gałęzi odbiornika

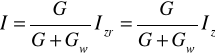
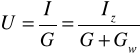
Napięcie na zaciskach odbiornika

---
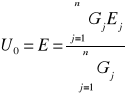
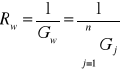
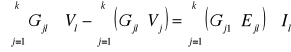
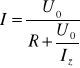