Łukasz Rafałowski BUDOWNICTWO ROK I GRUPA 4
Ćwiczenie 73
Wyznaczanie stężenia roztworu cukru za pomocą polarymetru
Wprowadzenie:
Polaryzacja światła:
Zjawiska dyfrakcji i interferencji wskazują na falową naturę światłą, zjawisko polaryzacji światła świadczy, że są to fale poprzeczne.
Falą elektromagnetyczną nazywamy zaburzenie pola magnetycznego, rozchodzące się w przestrzeni ze skończoną prędkością c. Jest to fala poprzeczna.
Jeżeli wektor drga tylko w jednej płaszczyźnie, zwanej płaszczyzną drgań, to światło jest liniowo spolaryzowane. Wektor magnetyczny B drga wówczas w płaszczyźnie prostopadłej do płaszczyzny drgań wektora E, zwanej płaszczyzną polaryzacji.
Ponieważ wiadomo, że wektor elektryczny odpowiedzialny jest za wszystkie zjawiska optyczne i fotograficzne, dalej będziemy mówić tylko o drganiach wektora elektrycznego.
Jeżeli światło spolaryzowane liniowo ma pewną składową niespolaryzowaną, to mówimy, że jest ono częściowo spolaryzowane.
Istnieje także polaryzacja kołowa, w której koniec wektora elektrycznego nie wykonuje drgań tam i z powrotem w płaszczyźnie, ale ma ustaloną wartość i zakreśla okrąg wokół kierunku rozchodzenia się. Najbardziej ogólnym przypadkiem polaryzacji jest polaryzacja eliptyczna, która określa wszystkie przypadki pośrednie pomiędzy polaryzacją kołową i liniową.
Światło naturalne jest niespolaryzowane.
Polaryzacja światła przez odbicie i załamanie:
Gdy wiązka światła pada, np. na powierzchnię płyty szklanej, część wiązki wnika do wnętrza, a część zostaje odbita, Jeżeli światło padające jest światłem naturalnym, niespolaryzowanym, to okazuje się, że obie wiązki, odbita i załamana, staja się częściowo spolaryzowane.
Polaryzację przez odbicie można wytłumaczyć następująco: światło pobudza atomy materiału, na który pada i reemisja wywołana tymi drganiami jest właśnie światłem odbitym. Ale tylko drgania, które są prostopadłe do płaszczyzny padania mogą dawać swój wkład. Te, które leżą w płaszczyźnie padania, nie mająskłądowych do kierunku obserwacji i dlatego nie mogą być emitowane w tym kierunku.
Polaryzacja światła przez podwójne załamanie:
W krysztale dwójłomnym światło ma dwie prędkości zależnie od tego, jak zorientowana jest płaszczyzna jego drgań. Gdy światło niespolaryzowane przechodzi przez dwójłomny kryształ, to rozdziela się na dwie części; promień zwyczajny i promień nadzwyczajny - spolaryzowane liniowo w różnych kierunkach i inaczej załamywane. Promień zwyczajny spełnia prawo załamania światła, natomiast promień nadzwyczajny nie. Kryształ taki byłby dobrym polatyzatorem, gdyby można było wyeliminować jedną z wiązek światła - zrealizowano to w pryzmacie Nicola.
Polaryzacja światła przez selektywną absorpcję:
Jeżeli światło niespolaryzowane pada na cienką płytkę wyciętą z turmalinu w taki sposób, że ściany są równoległe do osi optycznej kryształu, to zostaje ono rozdzielone na dwie składowe, liniowo spolaryzowane w ortogonalnych płaszczyznach. Jedna ze składowych jest silniej pochłaniana przez kryształ, druga natomiast przechodzi przez kryształ bez większych strat. Światło wychodzące z kryształu będzie więc liniowo spolaryzowane.
Wyznaczanie kąta spłaszczenia płaszczyzny polaryzacji:
Ciało polaryzujące światło nazywamy polaryzatorem, natomiast polaryzator wykorzystywany w celu stanu polaryzacji analizatorem. Gdy polaryzator i analizator są skrzyżowane, światło nie jest przez nieprzepuszczane.
Ale jeżeli np. roztwór cukru wprowadzony zostanie pomiędzy polaryzator i analizator stwierdzimy, że substancja ta skręca płaszczyznę polaryzacji światła. Przez obrót analizatora znaleźć można nową pozycję wygaszania, różną od poprzedniej. Efekt ten, znany jako skręcenie płaszczyzny polaryzacji, jest przejawem aktywności optycznej ośrodka.
Kąt skręcenia płaszczyzny polaryzacji światłą jest proporcjonalny do długości drogi przebytej przez światło w substancji. W przypadku roztworu, kąt skręcenia α dla danej barwy światła i długości drogi l jest proporcjonalny do stężenia d substancji aktywnej w roztworze:
α=adl, gdzie
l - długość rurki R
a - zdolność skręcająca.
Wykonanie ćwiczenia oraz obliczenia:
Zapalamy lampę z żółtym filtrem i ustawiamy lunetkę na ostrość.
Rurę R wypełniamy wodą destylowaną i ponownie regulujemy ostrość widzenia.
Obracamy analizator A do położenia, w którym środkowy pas i pozostała część pola widzenia są jednakowo ciemne. Odczytujemy wskazania α0i na podziałkach obu noniuszy. Pomiar powtarzamy trzykrotnie.
* 1: αa=0 ; αb=0
* 2: αa=-0.5 ; αb=-0.5
* 3: αa=0 ; αb=0
Obliczamy wartość średnią ![]()
Rurę R przepłukujemy, napełniamy roztworem o znanym stężeniu ( 5g/dm3) i przeprowadzamy pomiar wartości α1i', jak w punkcie 3.
* 1: αa=5,5 ; αb=5,5
* 2: αa=5,5 ; αb=5,5
* 3: αa=5,5 ; αb=5,5
Obliczamy wartość średnią: ![]()
Obliczamy kąt skręcenia płaszczyzny polaryzacji: ![]()
Obliczamy zdolność skręcania: 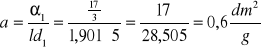
Różnica odczytów dla roztworu I i dla wody destylowanej daje kąt skręcenia płaszczyzny polaryzacji: α1=α1'-α0=5,5+1/6=33/6. Znając długości rurki R i stężenie d1 roztworu I, znajdujemy zdolność skręcającą.
Rurę R wypełniamy teraz roztworem II o nieznanym stężeniu d2.
* 1: αa=9,5 ; αb=9,5
* 2: αa=9,5 ; αb=9,5
* 3: αa=9,0 ; αb=9,0
Znajdujemy kąt skręcenia α2 płaszczyzny polaryzacji dla roztworu II: α2=α2'-α0, gdzie
![]()
Więc ![]()
Obliczamy nieznane stężenie d2 roztworu II:
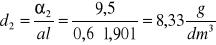
Przeprowadzamy rachunek błędów

, ale
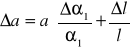
, więc
![]()
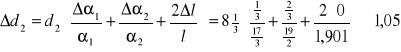
Wnioski:
Dzięki użyciu polarymetru doszliśmy do wniosku, że płaszczyzna polaryzacji światłą została skręcona. Zauważyliśmy również, że woda destylowana nie skręca jej (więc jest optycznie nieczynna), natomiast roztwór cukru o stężeniu 5g/dm3 skręca ją o kąt 5,66 (jest więc optycznie czynny). Jednym słowem potwierdziło się nasze założenie, że roztwór cukru skręca płaszczyznę polaryzacji.
Ponadto dzięki znajomości kąta skręcenia α2 możemy obliczyć nieznane stężenie d2 roztworu tego samego rodzaju.
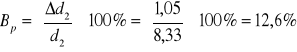
Wyszukiwarka
Podobne podstrony:
Ćwiczenie 73, Ćwiczenie 73 (4), Ćwiczenie 73
Ćwiczenie 73, WYDZIAŁ
Ćwiczenie 73, Ćwiczenie 73 (8), EWELINA WAJS
Ćwiczenie 73, Ćwiczenie 73 (3), Adam Wasilewski
Ćwiczenie 73
cwiczenia EK D zad 3 17 2007
Cwiczenie 17 Wzor sprawozdania id 125192
Cwiczenie 17 z 1 2 i
Prawo cywilne - ćwiczenia 17.11.2008, Prawo cywilne(16)
Fizykoterapia Cwiczenia 6 id 17 Nieznany
Ćwiczenie 17
cwiczenie 17
Ćwiczenie nr 17, Studia, Fizyka, LABORKI
Cwiczenia wstepne1 17
Fizykoterapia Cwiczenia 5 id 17 Nieznany
cwiczenie 17 id 125181 Nieznany
więcej podobnych podstron