Pozycja obliczeniowa 2. Stropy
2.1 USTALENIE SCHEMATU STYTYCZNEGO, ZESTAWIENIE OBCIĄŻEŃ, OBLICZENIE SIŁ PRZEKROJOWYCH W STROPIE POD ŚCIANKĄ DZIAŁOWĄ
Założenia: 2x belki prefabrykowane obciążone częściowo równoległą ścianą działową zbudowaną z cegły dziurawki.
Schemat statyczny:
1. Podpora w ścianie zewnętrznej
Sprawdzenie warunków częściowego utwierdzenia:
a) Powyżej stropu i pod stropem wymurowana jest ściana, średnie naprężenie obliczeniowe 0,25≤ σobl
Ciężar własny ściany nad wieńcem:
Dach (poz. obl. Dach, rys 1.5):
(1,968/0,75)*0,72=1,889 kN
Razem: 1,889 kN
Mur na poddaszu + strop poddasza:
Mur:
Cegła pełna: 18 kN/m3 (0,25m)
Wełna mineralna: 2 kN/m3 (0,12m)
Wysokość muru: 2,60m
Szerokość muru: 0,25m+0,12m
0,25*18*2,60*0,72=11,7 , wartość obliczeniowa siły: 11,43*1,1=12,87
0,12*2*2,60*0,72=0,624 kN , wartość obliczeniowa siły: 0,610*1,2=0,749
Strop poddasza:
Ciężar przenoszony przez belki: (6,10+6,20*0,72(obciążenie zastępcze ściany działowej)*1/2=10,56 kN
Ciężar wieńca: 0,72*0,25*0,24*25=1,08 (przyjęto beton zbrojony zagęszczony)
wartość obliczeniowa siły: 0,60*1,3=1,404
Razem: 25,6 kN
Mur na parterze:
Cegła pełna: 18 kN/m3 (0,25m)
Wełna mineralna: 2 kN/m3 (0,12m)
Wysokość muru: 2,54m
Szerokość muru: 0,25m+0,12m
0,25*18*2,54*0,72=8,23 kN , wartość obliczeniowa siły: 11,43*1,1=9,05 kN
0,12*2*2,54*0,72=0,439 kN , wartość obliczeniowa siły: 0,610*1,2=0,527 kN
N= 9,577 kN
Nobl=36,07 kN
A=0,25*0,72=0,18
Naprężenie obliczeniowe wynosi:
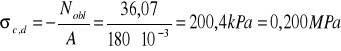
Projektowana podpora nie spełnia tego warunku na częściowe utwierdzenie.
b) strop oparty jest na ścianie za pośrednictwem wieńca żelbetowego o szerokości c równej grubości ściany t i nie mniejszej od wysokości konstrukcji stropu h.
Jak widać na schemacie obok projekt oparcia spełnia ten warunek na częściowe utwierdzenie
c) z końców żeber wypuszczone są pręty zbrojenia górnego (o przekroju wystarczającym do przeniesienia momentu utwierdzenia) zaopatrzone w haki wchodzące w winiec (niekonieczne w przypadku stali żebrowanej)
Biorąc pod uwagę błędy wykonawcze, projektowe oraz późniejsze przebudowy i modernizacje budynku zaprojektowano pręty zbrojenia górnego wykonane ze stali żebrowanej mogące przenieść moment utwierdzenia wynoszący 4/5 M0, czyli 5,04 [kNm] (rys. tech. 7 szczegół 3)
Projekt oparcia spełnia ten warunek na częściowe utwierdzenie
2. Podpora w ścianie wewnętrznej
Sprawdzenie warunków częściowego utwierdzenia:
a) Powyżej stropu i pod stropem wymurowana jest ściana, średnie naprężenie obliczeniowe 0,25≤ σobl
Jedyne obciążenie powyżej stropu to ściana działowa zbudowana z cegły dziurawki. Nie przenosi ona sił z wyższych kondygnacji. Nie stanowi również sama w sobie wystarczającego obciążenia (około 6 kN), aby mogły powstać odpowiednie naprężenia.
Projektowana podpora nie spełnia tego warunku na częściowe utwierdzenie.
b) strop oparty jest na ścianie za pośrednictwem wieńca żelbetowego o szerokości c równej grubości ściany t i nie mniejszej od wysokości konstrukcji stropu h.
Jak widać na powyższym schemacie projekt oparcia nie spełnia tego warunku na częściowe utwierdzenie
c) Projektowane podparcie nie spełnia dwóch powyższych warunków. W związku z tym nie ma potrzeby projektowania dodatkowego zbrojenia.
Projekt oparcia nie spełnia tego warunku na częściowe utwierdzenie.
Wniosek:
Schematem statycznym dla projektowanego stropu jest belka swobodnie podparta.
Długość obliczeniowa:
Ln=2,48 m
Leff=2,48+2*2,5%*2,48=2,60 m
Długość modularna belki przyjętej w projekcie 2,70 m
Obciążenie:
Na długości 152 cm (Ln+5%Ln-(102+2,5%Ln)
Rodzaj obciążenia |
Wartość charakterystyczna [kN/m] |
Współczynnik |
Wartość obliczeniowa |
Panele podłogowe 0,72*0,015 |
0,0108 |
1,2 |
0,0130 |
Gładź cementowa 0,72*0,035*21,0 |
0,5292 |
1,3 |
0,6880 |
Styropian 0,72*0,02*0,45 |
0,0065
|
1,2 |
0,0078 |
Strop Teriva I 0,72*2,68 |
1,9296 |
1,1 |
2,1226 |
Tynk cementowo - wap. 0,72*0,01*19,0 |
0,1368 |
1,3 |
0,1778 |
Razem obciążenia stałe g: |
2,6129 |
- |
3,0092 |
Obciążenie technologiczne p: 1,5 |
1,5000 |
1,4 |
2,1000 |
Obciążenie całkowite G=g+p |
4,1129 |
- |
5,1092 |
Na długości Leff-152 =108
Rodzaj obciążenia |
Wartość charakterystyczna [kN/m] |
Współczynnik |
Wartość obliczeniowa |
Panele podłogowe ½*(0,72-0,12)*0,015 |
0,0045 |
1,2 |
0,0054 |
Płytki ceramiczne ½*(0,72-0,12)*0,008*21,0 |
0,0504 |
1,2 |
0,0605 |
Gładź cementowa (0,72-0,12-0,04)*0,035*21,0 |
0,4112 |
1,3 |
0,5351 |
Styropian (0,72-0,12) *0,05*0,45 +2*0,02*0,035*0,45 |
0,0055
|
1,2 |
0,0066 |
Strop Teriva I 0,72*2,68 |
1,9296 |
1,1 |
2,1226 |
Tynk cementowo - wap. 0,72*0,01*19,0 |
0,1368 |
1,3 |
0,1778 |
Ściana działowa: Tynk gipsowy 2,54*0,04*12,0 Cegła dziurawka 2,54*0,12*14,0 |
1,2192
4,2672 |
1,3
1,1 |
1,5850
4,6939 |
Razem obciążenia stałe g: |
8,0244 |
- |
9,1869 |
Obciążenie technologiczne p: 1,5 |
1,5000 |
1,4 |
2,1000 |
Obciążenie całkowite G=g+p |
8,5244 |
- |
11,2869 |
Obliczenie sił wewnętrznych, obliczenie momentu obliczeniowego dla przyjętego przekroju, sprawdzenie stanu granicznego nośności oraz stanu granicznego użytkowalności.
Obliczenie sił występujących w belce.
Schemat statyczny obliczanego żebra:
Maksymalny moment zginający Mt obliczono wg normy: PN-B-03264:2002
Założenia:
Msd=5,70 [kNm]
Przyjęto przekrój złożony z dwóch belek Teriva o:
beff= 0,72 m
hf=0,03 m
h=0,24 m
b=0,2 m
d=24-2=22 cm = 0,22m
a2=24-17,4= 6,6 cm=0,066 m
belka swobodnie podparta
beton klasy B20 o:
wytrzymałość charakterystyczna na ściskanie fck=16 [MPa]
wytrzymałość charakterystyczna na rozciąganie fctk=1,3 [MPa]
wytrzymałość średnia na rozciąganie fctm=1,9 [MPa]
wytrzymałość obliczeniowa na ściskanie fcd=10,6 [MPa]
wytrzymałość obliczeniowa na rozciąganie fctd=0,87 [MPa]
Stal zbrojeniowa: A-III 34GS i fyk=410 MPa, fyd=350 [Mpa]
AS1=2*(2*3,14*(0,008)2) = 0,000804 m2
AS2=1/2*AS1=0,000402 m2
Obliczam xeff,lim:
Korzystając z tabeli dla stali klasy A-III obliczam x eff,lim:
![]()
Obliczam x eff: (co prawda liczę to nie potrzebnie, ponieważ xeff może mieć maksymalnie wartość xeff,lim które wynosi 0,12 m w tym przypadku wycięte pole przekroju będące w strefie ściskanej ma swój środek ciężkości na pewno bliżej krawędzi ściskanej (poniżej 0,6 m - przekrój teowy z półką górną) niż środek ciężkości prętów ściskanych (0,066 m), co oznacza że można przejść od razu do obliczenia Mt - wzór ten jednak znajduje się na końcu analizowanej krok po kroku normy)
fyd*As1=fcd*(beff* hf +b*(xeff-hf)+fyd*As2
fyd*As1-fyd*As2 =fcd* beff* hf + fcd*b* xeff - fcd*b* hf
fyd*As1-fyd*As2 -fcd* beff* hf + fcd*b* hf = +fcd*b* xeff
![]()
i ![]()
więc do obliczeń przyjmuje ![]()
m
Ponieważ środek ciężkości zbrojenia ściskanego znajduje się dalej od krawędzi ściskanej, niż środek ciężkości pola przekroju strefy ściskanej obliczam Mt ze wzoru:
Uwagi: MRd w normie = Mt w opracowaniu

Msd = 6,7 [kNm] i MSd<Mt
Warunek na moment maksymalny został spełniony.
Wartości dopuszczalnych obciążeń przypadających na jedną belkę (całkowite obciążenie obliczeniowe maksymalne = 5,52 kN) nie zostały przekroczone.
Ostatecznie przyjęto dwie belki TERIVA I o dł. modularnej 2,7m.
2.2 USTALENIE SCHEMATU STYTYCZNEGO, ZESTAWIENIE OBCIĄŻEŃ, OBLICZENIE SIŁ PRZEKROJOWYCH W STROPIE TERIVA I
1. Ustalenie schematu statycznego, rozpiętości obliczeniowej i obciążeń.
Schemat statyczny:
1. Podpora w ścianie zewnętrznej
Sprawdzenie warunków częściowego utwierdzenia:
a) warunek 1: Powyżej stropu i pod stropem wymurowana jest ściana, średnie naprężenie obliczeniowe 0,25≤ σobl
Ciężar własny ściany nad wieńcem:
Dach (poz. obl. Dach, rys 1.5):
(1,968/0,75)*0,6=1,574 kN
Razem: 1,574 kN
Mur na poddaszu + strop poddasza:
Mur:
Cegła pełna: 18 kN/m3 (0,25m)
Wełna mineralna: 2 kN/m3 (0,12m)
Wysokość muru: 1,80 m
Szerokość muru: 0,25m+0,12m
0,25*18*1,80*0,6=8,1 kN , wartość obliczeniowa siły: 8,1*1,1=8,91 kN
0,12*2*1,80*0,6=0,432 kN , wartość obliczeniowa siły: 0,610*1,2=0,518 kN
Strop poddasza:
Ciężar przenoszony przez belki: 4,5212*5,7*1/2=13,13 kN
Ciężar wieńca: 0,60*0,25*0,24*25=0,9 (przyjęto beton zbrojony zagęszczony)
Wartość obliczeniowa siły: 0,90*1,3=1,17 kN
Razem: 23,73 kN
Mur na parterze:
Cegła pełna: 18 kN/m3 (0,25m)
Wełna mineralna: 2 kN/m3 (0,12m)
Wysokość muru: 2,54m
Szerokość muru: 0,25m+0,12m
0,25*18*2,54*0,6=6,86 kN , wartość obliczeniowa siły: 6,86*1,1=7,54 kN
0,12*2*2,54*0,6=0,37 kN , wartość obliczeniowa siły: 0,37*1,2=0,44 kN
N= 7,98 kN
Nobl=33,28 kN
A=0,25*0,72=0,18
Naprężenie obliczeniowe wynosi: 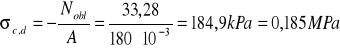
Projektowana podpora nie spełnia tego warunku na częściowe utwierdzenie.
b) warunek 2: strop oparty jest na ścianie za pośrednictwem wieńca żelbetowego o szerokości c równej grubości ściany t i nie mniejszej od wysokości konstrukcji stropu h.
Jak widać na schemacie obok projekt oparcia spełnia ten warunek na częściowe utwierdzenie
c) warunek 3: z końców żeber wypuszczone są pręty zbrojenia górnego (o przekroju wystarczającym do przeniesienia momentu utwierdzenia) zaopatrzone w haki wchodzące w winiec (niekonieczne w przypadku stali żebrowanej)
Biorąc pod uwagę błędy wykonawcze, projektowe oraz późniejsze przebudowy i moderni-zacje budynku zaprojektowano pręty zbrojenia górnego wykonane ze stali żebrowanej mogące przenieść moment utwierdzenia wynoszący 4/5 M0, czyli 0,8*3,4=2,72 kNm.
Projekt oparcia spełnia ten warunek na częściowe utwierdzenie
2. Podpora w ścianie wewnętrznej
Sprawdzenie warunków częściowego utwierdzenia:
a) Powyżej stropu i pod stropem wymurowana jest ściana, średnie naprężenie obliczeniowe 0,25≤ σobl
Ciężar własny ściany nad wieńcem:
Ściana działowa na poddaszu + strop poddasza:
Ściana:
Cegła pełna: 18 kN/m3 (0,25m)
Gładź cementowa: 21 kN/m3 (0,04m)
Wysokość muru: 3,20m
Szerokość muru: 0,25m+0,04m
0,25*18*3,6*0,6=9,72 kN , wartość obliczeniowa siły: 8,1*1,1=10,69 kN
0,04*21*3,6*0,6=1,81 kN , wartość obliczeniowa siły: 0,610*1,2=2,17 kN
Strop poddasza:
Ciężar przenoszony przez belki: 4,5212*5,7*1/2=13,13 kN
Ciężar wieńca: 0,60*0,25*0,24*25=0,9 (przyjęto beton zbrojony zagęszczony)
Wartość obliczeniowa siły: 0,90*1,3=1,17
Razem: 27,16 kN
Mur na parterze:
Cegła pełna: 18 kN/m3 (0,25m)
Wełna mineralna: 2 kN/m3 (0,12m)
Wysokość muru: 2,54m
Szerokość muru: 0,25m+0,12m
0,25*18*2,54*0,6=6,86 kN , wartość obliczeniowa siły: 6,86*1,1=7,54 kN
0,12*2*2,54*0,6=0,37 kN , wartość obliczeniowa siły: 0,37*1,2=0,44 kN
N= 7,98 kN
Nobl=35,14 kN
A=0,25*0,72=0,18
Naprężenie obliczeniowe wynosi:
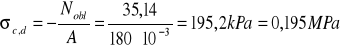
Projektowana podpora nie spełnia tego warunku na częściowe utwierdzenie.
b) strop oparty jest na ścianie za pośrednictwem wieńca żelbetowego o szerokości c równej grubości ściany t i nie mniejszej od wysokości konstrukcji stropu h.
Jak widać na na schemacie obok projekt oparcia spełnia ten warunek na częściowe utwierdzenie
c) warunek 3: z końców żeber wypuszczone są pręty zbrojenia górnego (o przekroju wystarczającym do przeniesienia momentu utwierdzenia) zaopatrzone w haki wchodzące w winiec (niekonieczne w przypadku stali żebrowanej)
Biorąc pod uwagę błędy wykonawcze, projektowe oraz późniejsze przebudowy i modernizacje budynku zaprojektowano pręty zbrojenia górnego wykonane ze stali żebrowanej mogące przenieść moment utwierdzenia wynoszący 4/5 M0,
czyli 0,8*3,40=2,72 kNm.
Wniosek:
Schematem statycznym dla projektowanego stropu jest belka swobodnie podparta.
Długość obliczeniowa:
Ln=5,7 m
Leff=5,7+2*2,5%*5,7= 5,99 m
Długość modularna belki przyjętej w projekcie 6,0 m
Obciążenie:
Rodzaj obciążenia |
Wartość charakterystyczna [kN/m] |
Współczynnik |
Wartość obliczeniowa |
Panele podłogowe 0,60*0,015 |
0,009 |
1,2 |
0,011 |
Gładź cementowa 0,60*0,035*21,0 |
0,441 |
1,3 |
0,573 |
Styropian 0,60*0,05*0,45 |
0,005
|
1,2 |
0,006 |
Strop Teriva I 0,60*2,68 |
1,608 |
1,1 |
1,769 |
Tynk cementowo - wap. 0,60*0,01*19,0 |
0,114 |
1,3 |
0,148 |
Razem obciążenia stałe g: |
2,177 |
- |
2,507 |
Obciążenie technologiczne p: 1,5 |
1,500 |
1,4 |
2,100 |
Obciążenie całkowite G=g+p |
3,677 |
- |
4,607 |
Obliczona w tabeli wartość charakterystyczna obciążenia całkowitego wynosi 3,68 kN i jest mniejsze od dopuszczalnej wartości charakterystycznej równej 6,22 kN
Ostatecznie przyjęto belkę o Teriva I o rozpiętości modularnej 6,0 m.
h=24cm
c=25cm
t=25cm
t=25cm
c=18cm
h=24cm
![]()
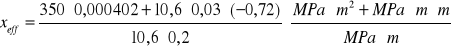
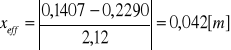
h=24cm
c=25cm
t=25cm
h=24cm
c=25cm
t=25cm
Wyszukiwarka
Podobne podstrony:
opis techniczny
opis techniczny
PKS W zad3 Opis Techniczny
Kopia Opis techniczny B, Skrypty, UR - materiały ze studiów, studia, studia, 4 STASZEK, Semestr II,
OPIS TECHNICZNY, Skrypty, PK - materiały ze studiów, II stopień, pomoc, II semestr, KONSTRUKCJE STAL
PWiK - Opis techniczny, Budownictwo S1, Semestr IV, PWiK, Projekt, Projekt 4
Opis techniczny-moje, Inżynieria Środowiska, Przydomowe oczyszczalnie ścieków, projekt, Przydomowe o
Opis Techniczny
OPIS TECHNICZNY PROJEKTU
opis techniczny
Opis techniczny usługowo przemysłowy
opis techniczny do rysunkow
Opis techniczny
6082 PB 7C PERONY opis techniczny
Opis techniczny 3
Instalacje budowlane Projekt Opis techniczny
PB opis techniczny
Opis techniczny 26
Opis techniczny Telekomunikacja Naglosnienie
więcej podobnych podstron