Wieteska Emilia dnia 19.03.02r.

gr. 10

P58. Badanie zjawiska dyfrakcji na pojedynczej i podwójnej szczelinie.

Celem mojego ćwiczenia jest badanie natury światła poprzez analizę zjawiska dyfrakcji na pojedynczej i podwójnej szczelinie. Zjawisko dyfrakcji światła, polega na uginaniu się promieni świetlnych napotykających na swojej drodze przeszkody, w wyniku, czego występują odstępstwa od prostoliniowego ich biegu, jest to ściśle związane z falową naturą światła.

Dyfrakcja i interferencja światła.

Zjawiska dyfrakcji i interferencji promieni świetlnych wskazują na falową naturę światła. Światło, przechodzące przez szczeliny o wymiarach porównywalnych z długością fali, ulega ugięciu, bowiem zgodnie z zasadą Huygensa, każda szczelina staje się źródłem nowej fali i wysyła promienie we wszystkich kierunkach.

Dyfrakcją nazywamy zjawisko ugięcia się fali na otworach bądź krawędziach przesłony, czyli uginaniem prostoliniowego biegu promieni. Ugięte wiązki, padające w to samo miejsce ekranu, ulegają interferencji.

Interferencją fal nazywamy nakładanie się fal o tej samej częstotliwości, powodujące wzmocnienie lub osłabienie natężenia fali wypadkowej. W tych miejscach ekranu, w których ugięte promienie spotykają się w zgodnych fazach, następuje ich wzmocnienie i powstają jasne prążki interferencji. Jeżeli odległość ekranu od szczeliny l jest znacznie większe, niż odległość pomiędzy szczelinami d, ( l >> d ), to r₂-r₁=BC=dsin . Mamy, więc następujące warunki wystąpienia maksimów i minimów interferencji.

dsin_n=n -warunek wystąpienia maksimum rzędu n

dsin_n=(2n+1) -warunek wystąpienia minimum rzedu n

Warunki te określają kąty ugięcia promieni, pod którymi na ekranie zobaczymy prążki jasne (wzmocnienie) i ciemne (wygaszenie).

Dyfrakcja na szczelinie o szerokości a> .

Gdy fala świetlna pada na pojedynczą szczelinę na ekranie otrzymujemy obraz dyfrakcyjny złożony z jasnych i ciemnych prążków- tym razem jednak jasne prążki nie mają jednakowego natężenia. Najjaśniejszym prążkiem jest prążek rzędu zerowego, położony na prawo, na lewo od niego mają tym mniejsze natężenie, im wyższy jest ich rząd. Dyfrakcja spowodowana jest nakładaniem się fal pochodzących z różnych części szczeliny.

Warunek wystąpienia minimum w obrazie dyfrakcji ma postać:

Asin_k k=1,2……..

gdzie a-szerokość szczeliny, k-rząd minimum.

Typowym przedstawicielem lasera gazowego jest laser helowo-neonowy (=632,8nm) z którego korzystam podczas wykonywania mojego ćwiczenia. Podstawową częścią tego lasera jest rurka szklana lub kwarcowa wypełniona mieszaniną helu i neonu, pod bardzo małym ciśnieniem (ciśnienie cząstkowe p_He=130 Pa, p_Ne=13Pa). Do rury wlutowane są elektrody, do których przykłada się napięcie powodujące wyładowanie elektryczne i w efekcje, wzbudzenie atomów, które emitują spontanicznie światło, widziane w postaci świecenia rury laserowej.

Do wykonania ćwiczenia muszę mieć:

• Interfejs Science Workshop 500

• Czujnik ruchu obrotowego

• Slajd z pojedyńczą i podwójną szczeliną

• Laser (helowo-neonowy)

• Ława optyczna, statyw

• Sonda światłowodowa

Wykonanie ćwiczenia:

1. Przygotowanie układu pomiarowego:

• Podłączyć wtyki czujnika ruchu obrotowego do cyfrowych wejść 1 i 2 interfejsu.

• Podłączyć czujnik światła do analogowego kanału A interfejsu.

• Przygotowanie komputera:

• Włączam interfejs i komputer.

• Uruchamiam system operacyjny Windows i program Scence Workshop. Otwieram dokument P58_DIFF.SWS, który jest w katalogu Library/Pfysics.

• Ustawiam częstość pomiaru na 100 Hz.

• Przebieg i rejestracja pomiarów dla:

Dyfrakcja na pojedynczej szczelinie:

• Włączam źródło światła laserowego.

• Ustawiam slajd z pojedynczą szczeliną na drodze światła w odległości ok. 10cm od lasera.

• Ustawiam źródło światła względem slajdu tak, aby na ścianie (ekranie), widoczne były wyraźne, ostre prążki (jest to obserwacja światła czerwonego.

• Umieszczam końcówkę światłowodu w uchwycie na końcu liniowego ramienia czujnika ruchu w odległości od 100 do 150cm od slajdu ze szczeliną.

• Rozpoczynam pomiar przy pomocy komputera, w którym naciskam przycisk REC (rozpoczyna się pomiar), jednocześnie przesuwając powoli, płynnie końcówkę światłowodu obracając pokrętłem czujnika ruchu tak, aby znajdował się on w świetle lasera.

• Po zakończeniu przesuwu światłowodu zatrzymuję pomiarkowanie i otrzymuję w komputerze wykres danego pomiaru. Na którym pojawia się maksimum natężenia dla rzędu zerowego i znacznie mniejsze maksimum odpowiadające wzmocnieniu światła laserowego.

Analiza danych

Obliczam szerokość szczeliny a. Zgodnie z poniższym wzorem dla k=1

a=/sin_

Sinus kąta ₁, pod którym obserwowane jest pierwsze minimum, można obliczyć ze wzoru.

Sin_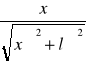


Gdzie x-odległość od środka wzmocnienia rzędu 0 do pierwszego minimum, l-odległość od szczeliny do płaszczyzny ruchu końcówki światłowodu.

Obliczam x (pomiar ten odczytuję z wykresu)

x=1,366cm-0,921cm=0,445cm

l=103,5cm

Obliczam sin₁

Sin₁=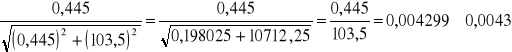


Obliczam szerokość szczeliny a

=632,8nm (długość fal, odczytana z obudowy lasera)

a=
, przeliczam na milimetry




Obliczam błąd porównując obliczoną szerokość szczeliny a, z wartością a_r, podaną na oprawie slajdu. Korzystam ze wzoru:

B_p=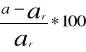
%

A_r= 0,16mm

B_p=
%=8% (błąd)

Dyfrakcja na podwójnej szczelinie

Przeprowadza się ją tak samo jak dyfrakcję na pojedynczej szczelinie z jedną różnicą zamiast slajdu z pojedynczą szczeliną ustawiam slajd z podwójną szczeliną, na drodze promieniowania laserowego.

Analiza danych

Obliczam odległość d pomiędzy szczelinami. Korzystam ze wzoru:

Dsin_n=n , gdzie n=1

Wyprowadzam d ze wzoru:

d=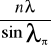
,

Sinus kąta ugięcia rzędu n dany jest następującą zależnością.

Sin_n=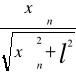


x-odległość x odczytuję z wykresu.

x=2,066cm-1,796cm=0,27cm

l-odległość szczeliny do płaszczyzny ruchu końcówki światłowodu.

l=104.5cm

sin=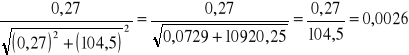


d=


zamieniam na mm




Obliczam błąd względny procentowy

B_p=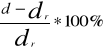
, d_r=0,25mm (odczytany z oprawy slajdu)

B_p=
(błąd pomiaru)

WNIOSKI

Gdy na drodze światła pojawi się przeszkoda wtedy mamy do czynienia z dyfrakcją światła, polegającą na ugięciu prostoliniowego biegu promieni, czego odwzorowaniem są następujące wykresy, wskutek czego występują minima i maksima rzędu n. Po przejściu wiązki promieni przez podwójną szczelinę, szerokość szczeliny w porównaniu do szerokości szczeliny przez pojedynczą jest o wiele większa.


---