Laboratorium fizyki |
||
Ćwiczenie nr O4. Badanie falowych właściwości światła |
||
Pluton I |
Grupa II |
Musialik Łukasz Pawlikowski Wojciech |
25 maj 2000 |
Ocena: |
|
Ćwiczenie to składało się z trzech części:
Pierwsza polegała na badaniu ugięcia (dyfrakcji) światła,
Druga na określeniu położenia płaszczyzny polaryzacji światła,
Trzecia na wyznaczeniu długości fali świetlnej za pomocą siatki dyfrakcyjnej
AD1)
Wąska szczelina, zgodnie z zasadą Huygensa , po dojściu do niej promienia świetlnego, staje się źródłem światła. Światło rozchodzi się poza nią we wszystkich kierunkach.
Dwa skrajne promienie wychodzące ze szczeliny uginają się pod kątem α, a na ekranie spotkają się w punkcie D. Różnica dróg tych promieni wynosi
Δ=AC
Z rysunku widać, że różnica tych dróg wynosi również
Δ=dsin αk
gdzie:
d- szerokość szczeliny,
αk- kąt ugięcia.
Wzmocnienie światła nastąpi w tych punktach ekranu, w których promienie będą spotkały się w fazach, zgodnych, a zatem gdy spełniony będzie warunek :
Δ=k λ
k=0;1;2;...
W tych miejscach na ekranie otrzymamy jasne prążki. Wygaszanie światła(ciemne prążki) nastąpi w punktach ekranu, w których promienie będą spotykały się w fazach przeciwnych.
W rezultacie na ekranie otrzymamy układ jasnych i ciemnych prążków.
Rozpatrzmy położenie k-tego prążka jasnego. Odległość tego prążka od osi wiązki światła, oznacza przez ak. Ostateczny wzór na szerokość szczeliny ma postać
d=k λ l/ak
AD2)
W tym doświadczeniu obserwowaliśmy polaryzacje światła przez podwójne załamanie.
Zjawisko to polega na tym, że przy wchodzeniu promienia do pewnych ośrodków promień padający dzieli się na dwa promienie: zwyczajny i nadzwyczajny. Promienie te biegną w
różnych kierunkach i są spolaryzowane liniowo, w płaszczyznach wzajemnie prostopadłych.
Wiązkę światła polaryzowaliśmy przy użyciu płyty polaryzacyjnej .
Przy pionowym położeniu polaryzatora obserwowaliśmy na ekranie promień o większym natężeniu, zaś przy poziomym położeniu promień ten był słabszy.
AD 3)
Siatka dyfrakcyjna jest to płaska powierzchnia z przezroczystymi rysami. Stała siatki to odległość między środkami dwóch sąsiednich szczelin. Jeżeli padnie promień świetlny na siatkę dyfrakcyjną, zgodnie z zasadą Huygensa każda szczelina jest źródłem fali rozchodzącej się we wszystkich kierunkach. Promienie ugięte po pewnym kątem ϕ interferują ze sobą i następuje zjawisko wygaszania lub wzmacniania. Na ekranie otrzymujemy układ prążków. Mierząc odległości między prążkami symetrycznymi względem osi promienia świetlnego możemy wyznaczyć długość fali światła.
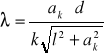
gdzie: ak - odległość prążka k-tego rzędu od osi,
l - odległość ekranu od siatki,
d - stała siatki dyfrakcyjnej.
Obliczenia (dotyczące punktu 1):
.....................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................
Z wyników zamieszczonych w tabeli I wnioskujemy , że doświadczenie przebiegało w sposób zadowalający. Wartość szerokości szczeliny wahała się między wartością 0,059 10-3 m do 0,062 10-3 m .Różnice w błędach obserwowane w tabelce są wynikiem niedoskonałości przyrządów wykorzystanych do doświadczenia oraz oka ludzkiego, które w pewnych momentach mogło być obarczone dużym błędem, szczególnie przy tak małych wartościach.Obliczenia (dotyczące punktu 3):
.................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................
.........................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................Wnioski:
Stała siatki dyfrakcyjnej z obliczeń wyniosła 0,01 10-3 .Wartość błędu obliczonego różniczką zupełną po zaokrągleniu do trzech miejsc po przecinku wyniósł zero. Przed zaokrągleniem wartość błędu względnego równy byłby jednościTABELA I
saaadaslp Lp |
Odległość szczeliny od ekranu l [m] |
Błąd pomiaru Δl [m] |
Rząd widma K |
Połowa odległości miedzy symetrycznymi prążkami ak [m] |
Błąd pomiaru Δak [m] |
Szerokość szczeliny d [m] |
Błąd Δd [m] |
d=Δd /d |
1
|
|
|
1 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
2 |
|
|
1 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
3 |
|
|
1 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
Odległość siatki od ekranu |
Rząd widma |
Położenie prążków |
Odległość średnia |
|||
l [m] |
Δl [m] |
K |
a' [m] |
a” [m] |
ak [m] |
Δak |
|
|
1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
3 |
|
|
|
|
Wyszukiwarka
Podobne podstrony:
4SPRAWOZDANIE DO CWICZENIA LABORATORYJNEGO Z FIZYKI BUDOWLI
SPRAWOZDANIE DO ĆWICZENIA LABORATORYJNEGO Z FIZYKI BUDOWLI2
04, Strona 1, Laboratorium fizyki
M D 04, LABORATORIUM
Wyznaczanie stosunku ładunku do masy elektronu, Laboratorium z fizyki - lab 1
Zastosowanie fotoogniwa do pomiarów fotometrycznych, Laboratorium z fizyki - cwiczenia
wyznaczanie stosunku e-m ładunku elektronu do jego masy metodą magnetonu-1, LABORATORIUM Z FIZYKI
Fizyka II s. Elektrostatyka 2, mechanika, BIEM- POMOCE, laborki z fizy, moje, laboratorium z fizyki,
Laboratorium fizyki CMF PŁ gut, Elektrotechnika PŁ, Inżynierskie, I st, 1 semestr, Fizyka, Laborator
Prezentacja II Laboratorium Fizyki BHP 2008 9
hydro tabele do 3, Hydrologia
tabele do cw 36, ATH, Fizyka, od sylwi, Fizyka, laborki, Fizyka, Fizyka
LABORATORIUM FIZYKI1
Instrukcja do ćwiczenia laboratoryjnego PDH
Sprawozdanie z laboratorium z fizyki
tabele do izolinii
więcej podobnych podstron