Wydział Inżynierii Elektrycznej i Komputerowej	Artur Karpisz	Zespół 1	Ocena ostateczna
Grupa 12	Badanie zależności oporu elektrycznego metali i półprzewodników od temperatury.	Nr ćwiczenia 13	Data 02.03.2001r.

1. OPRACOWANIE TEORETYCZNA

• Przewodnictwo metali.

Metale należą do dobrych przewodników elektrycznych. Ich dobre przewodnictwo jest wynikiem dużej liczby elektronów swobodnych. Opór elektryczny (rezystancja) metali wzrasta z temperaturą, przy czym metale czyste wykazują większą zależność oporu od temperatury niż stopy. Szczególnie niską wrażliwość na zmianę temperatury wykazują stopy Cu, Ni i Mn (manganin ,konstantan).

Atomy w metalu tworzą sieć krystaliczną, która nie jest idealną ze względu na znajdujące się w niej domieszki, luki(węzły sieci nie zajęte przez atomy), a także termiczne drgania sieci.

W wyniku rozpraszania elektronów na domieszkach i fononach(„kwantach” drgań sieci krystalicznej) pojawia się opór elektryczny. W niskich temperaturach rozpraszanie na domieszkach i defektach sieci dominuje nad rozpraszaniem na fononach i składa się na tzw. oporność resztkowa metalu. W czystych metalach jest ona bardzo mała, natomiast osiąga duże wartości w stopach. Dlatego opór stopów jest najczęściej większy od oporu czystych metali i słabo zależy od temperatury(np. dla konstantanu). Wraz ze wzrostem temperatury zwiększają się cieplne drgania atomów w sieci, co powoduje zakłócenie ruchu elektronów ukierunkowanych przez zewnętrzne pole elektryczne. Pojawia się opór elektryczny rosnący wraz z temperatura. Dla niewielkich przedziałów temperatury (kilkadziesiąt stopni) zmiana oporu jest wprost proporcjonalna do przyrostu temperatury i do oporu początkowego R₀:

ΔR=αR₀Δt.

Współczynnik proporcjonalności α nosi nazwę współczynnika temperaturowego oporu elektrycznego. Wyrażamy go w K^-1. Charakteryzuje on dany metal w określonym przedziale temperatur. Dla dużych przedziałów temperatur (rzędu kilkuset stopni) zależności oporu od temperatury nie da się już opisać funkcją liniową, tyko wyrażeniem:

R=R₀(1+αt+βt²+γt³),

gdzie α,β,γ są stałymi charakteryzującymi dany materiał.

Zależność oporu od temperatury została wykorzystana w praktyce do pomiaru temperatury w tzw. termometrach oporowych, gdzie jako materiał termoelektryczny stosowana jest platyna i nikiel

Omawiając zależność oporu od temperatury należy wspomnieć, że duża grupa metali nieferromagnetycznych i ich stopów oraz niektóre związki półprzewodnikowe, wykazują zjawisko tzw. nadprzewodnictwa. Polega ono na gwałtownym spadku ich oporu elektrycznego (prawie do zera) poniżej pewnej wartości temperatury. Zjawisko to znalazło zastosowanie w elektromagnesach do uzyskiwania bardzo silnych pól magnetycznych.

• Rezystory półprzewodnikowe

W półprzewodnikach przewodnictwo elektryczne zmienia się wraz z temperaturą na skutek zmian ruchliwości nośników(elektronów i dziur) na skutek rozpraszania na defektach i drganiach sieci, jak i wzrostu elektronów i dziur. Zwykle drugi sposób dominuje i opór elektryczny maleje wykładniczo wraz z temperaturą. Wzbudzenie elektronów do pasma przewodnictwa i powstanie dziur w paśmie walencyjnym nie jest tylko skutkiem dostarczenia energii elektrycznej. Opór może też zależeć oprócz temperatury od oświetlenia lub przyłożonego napięcia. Wyróżniamy więc: termorezystory(termistory i pozystory), fotorezystory i warystory.

Opór warystora zmniejsza się wraz ze wzrostem przyłożonego napięcia. Po przekroczeniu pewnej wartości jego opór staje się znikomo mały. Własność ta jest wykorzystywana w elektroenergetyce do zabezpieczania sieci w czasie wyładowań atmosferycznych.

Termorezystory wykazują silną zależność oporu od temperatury. Ponieważ opór elementów półprzewodnikowych nie jest funkcja liniową więc współczynnik temperaturowy oporu elektrycznego definiuje się wzorem różniczkowym:

gdzie
jest oporem w temperaturze t.

W praktyce stosuje się termorezystory o ujemnym współczynniku temperaturowym oporu, często są one nazywane termistorami, oraz o dodatnim współczynniku oporu nazywane pozystorami. Termistory wykonywane z półprzewodników będących tlenkami metali przejściowych (np. tlenku niklu NiO, tlenku miedzi CuO, dwutlenku tytanu
). Są one stosowane w obwodach żarzenia lamp elektronowych do zabezpieczania zimnych katod, kiedy ich opór jest mały, przed prądami udarowymi w chwili włączania. Ich współczynnik temperaturowy α_t jest ujemny w całym zakresie temperatur.

Dla termistorów zależność oporu od temperatury bezwzględnej T opisana jest dość dobrze wzorem:

gdzie A i B są stałymi o wymiarach oporu i temperatury, T jest temperaturą w skali Kelwina.

Podstawiając powyższy wzór do zależności na współczynnik temperaturowy oporu otrzymamy:

czyli ostatecznie otrzymujemy:

Pozystory są elementami ceramicznymi, w których głównym składnikiem jest tytanian baru BaTiO₃. stosuje się je w obwodach automatyki np. do zabezpieczania silników elektrycznych przed przegrzaniem. Nieznaczny dodatek jonów antymonu, bizmutu, itru, wolframu lub lantanu może spowodować obniżenie oporu właściwego BaTiO₃ z 10⁷÷10¹⁰Ω⋅m do 10^-1÷10Ω⋅m, zmianę w pewnym zakresie temperatur znaku współczynnika α_t z ujemnego na dodatni. Tak zmodyfikowany BaTiO₃ jest wykorzystywany do wyrobu pozystorów.

2. Opracowanie wyników pomiarów

• Tabela pomiarowa.

t [^oC]	T[^oK]
28,0	301	116,8	113,1	202,0	27,8
35,0	308	120,3	113,0	174,2	28,2
40,0	313	123,9	112,9	155,2	29,2
47,0	320	127,3	113,0	136,4	32,0
55,0	328	132,9	112,9	114,7	38,3
60,0	333	135,9	112,9	104,6	46,6
67,0	340	140,7	112,9	91,5	73,3
75,0	348	145,7	112,9	79,6	146,0
82,0	355	151,3	112,8	69,4	336,0
90,0	363	155,6	113,5	63,0	940,0

• Obliczam R₀ oraz współczynnik temperaturowy oporu α dla niklu

Korzystam ze wzoru:

R_t=R₀+αR₀t, gdzie R_t jest oporem w temperaturze t, R₀ - oporem w 0^oC

Podstawiam pierwsze dwie wartości R i t do powyższego wzoru i rozwiązuje układ równań:







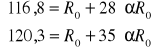
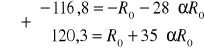
podstawiam αR₀ do jednego z równań układu i otrzymuję wartość R₀ niklu w t=0^oC



czyli


• Obliczam współczynniki A i B dla termistora





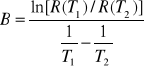
dla T₁=301 ^oK T₂=308 ^oK





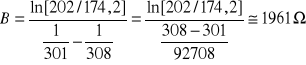
dla T₁=308 ^oK T₂=313 ^oK





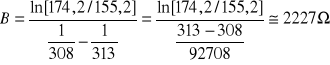
dla T₁=313 ^oK T₂=320 ^oK





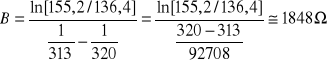
Uśredniam wyniki na podstawie trzech obliczeń:





Zapisuję opór termistora od T w postaci wykładniczej:


po podstawieniu wartości A i B otrzymałem:




• Tabela wartości α i T dla termistora
























t [^oC]	T [^oK]	αt
28	301	-0,0222
35	308	-0,0212
40	313	-0,0205
47	320	-0,0196
55	328	-0,0187
60	333	-0,0181
67	340	-0,0174
75	348	-0,0166
82	355	-0,0160
90	363	-0,0153

Obliczam współczynnik α dla pozystora metodą różniczkowania graficznego:





obliczam α dla β₁=42^o ,t=75^oC ,R=146Ω


więc


obliczam α dla β₁=6^o ,t=55^oC ,R=38,3Ω


więc


• Wnioski

Na podstawie wykonanych pomiarów i sporządzonych wykresów zależności oporu od temperatury można jednoznacznie stwierdzić, że potwierdziła się liniowa zależność metali od temperatury, co dobrze widać na wykresie zależności R(t) dla niklu. Natomiast krzywa R(t) konstantanu potwierdziła, że opór stopów słabo zależy od temperatury. Również charakterystyki R(t) termistora i pozystora nie odbiegały w znacznym stopniu od typowych charakterystyk tych elementów. Dlatego też mogę stwierdzić że ćwiczenie wykonano poprawnie, jednakże musimy sobie zdawać sprawę że pomiary spewnością są obarczone błędami.

4

Typowe charakterystyki dla: a - termorezytorów,

b - fotorezystorów, c - warystorów

---