20. Prawo Biota - Savarta - Laplace'a. Pole magnetyczne przewodnika kołowego.
Prawo to opisuje związek między wekt. indukcji magn. B(w.) a prądem płynącym w przewodniku wywołującym pole magn.:
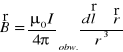
gdzie całka oznacza całkowanie po obwodzie z płynącym prądem (w przewodach o zaniedbywalnej grubości), dl(w.) - element długości obwodu, skierowany zgodnie z kierunkiem prądu, r(w.) - wektor łączący element dl(w.) z punktem, w którym liczymy wektor indukcji magnetycznej , μ0 - współczynnik proporcjonalności, zwany przenikalnością magnetyczną próżni (μ0=4π⋅10-7 H/m) , I - wartość natężenia prądu .
21. Prawo Ampere'a. Pole magnetyczne przewodnika prostoliniowego i solenoidu.
Prawo to opisuje związek między wekt. indukcji magn. B(w.) a prądem płynącym w przewodniku wywołującym pole magn.:
![]()
całka oznacza całkowanie po dowolnej krzywej zamkniętej, dl(w.) - element długości krzywej o kierunku zgodnym z kierunkiem wektora indukcji magnetycznej B(w.) , I - całkowitą wartość natężenia prądu zawartego wewnątrz krzywej, μ0 - współczynnik proporcjonalności, zwany przenikalnością magnetyczną próżni (μ0=4π⋅10-7 H/m) .
22. Moment magnetyczny. Moment siły i energia momentu magnetycznego.
F1
b
F2 F2
a
F2
F1 = J b B
F2 = J a B
Obliczamy moment pary sił działających na ramkę z prądem I.
F2
M= F2 b sinϕ
M= I a B b sinϕ
ϕ
M= I a b B sinϕ ;
M(w.)= r(w.)×F(w.), B B(w.)
M= r F sinϕ B sinϕ
M(w.)= m(w.) × B(w.),
m(w.)= I S n(w.) F2
mom. magn. obw. z prądem
n - wersor normalny do pow. obw. el
m(w.) M(w.) = m(w.) × B(w.)
M(w.) = p(w.) × E(w.)
WR = -p(w.) ⋅ E(w.)
I Wm = -m(w.) B(w.)
↑B(w.) ↑m W= -m(w.)B(w.) < 0
↑B(w.) →m W= 0
↑B(w.) ↓m W= -m(w.) B(w.)= mB >0
23. Oddziaływanie prądów elektrycznych.
Zob. np. odp. 27 „Samoindukcja i indukcja wzajemna”
24. Prawo Gaussa dla wektora indukcji magnetycznej B.
Prawo Gaussa dla pola B(w.)
![]()
26. Zjawisko indukcji elektromagnetycznej Faradaya. Siła elektromotoryczna indukcji.
Strumień pola magnetycznego B(w.) przechodzący przez obwód przewodnika wynosi:
![]()
Napięcie wywołane zmianą strumienia ΦB
![]()
- reguła przekory Lenza
ε - siła elektromotoryczna indukcji - [ε] = [V]
[ΦB] = [T ⋅ m2] = [Wb] - Weber
Fe'
←I Γ
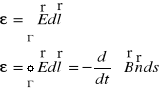
Z analizy wektorowej wiemy, że :
![]()
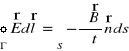
![]()
różniczkowa postać
prawa indukcji
elektr.magn. prawa
Faradaya
27. Samoindukcja i indukcja wzajemna. Współczynnik indukcji własnej L.
Każdy obwód z płynącym prądem wytwarza pole magnetyczne, którego linie przenikają również przez własny obwód. Jeżeli z jakichkolwiek powodów natężenie prądu w obwodzie ulegnie zmianie, zmieni się również strumień indukcji przechodzący przez ten obwód. To z kolei spowoduje powstanie siły elektromotorycznej, której kierunek będzie przeciwdziałał zmianom prądu. Takie zjawisko nazywa się samoindukcją.
εC=?
B ∼ I => ΦB ∼ B ∼ I
ΦB = L I (L - wsp.
R proporcjonalności
zwany wsp. ind.
własnej lub
indukcyjnością)
B
![]()
[L] = [V ⋅ s / A] = [Ω ⋅ s] = [H] (Henr)
------------------------
Jeżeli linie pola magnetycznego, wytworzone przez obwód 1, będą przenikać (w całości lub częściowo) przez obwód 2, to zmiana natężenia prądu w obwodzie 1, I1, wytworzy siłę elektromotoryczną ε2 w obwodzie 2. Jej wartość będzie proporcjonalna do szybkości zmian prądu w obwodzie 1, co zapisujemy równaniem:
ε2 = -M12 dI1/dt
Gdzie M12 oznacza współczynnik indukcji wzajemnej obwodu 1 względem obwodu 2.
Φ1= Φ11 + Φ12 | Φ11= L11I1 | Φ22= L22I2
Φ2= Φ22 + Φ21 | Φ12= L12I2 | Φ21= L21I1
ε1= - dΦ1/dt = - (dΦ11/dt + dΦ12/dt) = -(L11 dI1/dt + L12 dI2/dt)
ε1= - dΦ2/dt = - (dΦ22/dt + dΦ21/dt) = -(L22 dI2/dt + L21 dI1/dt)
L12 = L21 = M - współcz. indukcji wzajemnej
28. Pole magnetyczne materii. Wektor namagnesowania (magnetyzacja) M.
Oddziaływanie pola magn. na różne substancje:
a) diamagnetyki - słabo wypychane z pola magnetycznego
b) paramagnetyki - słabo wciągane do pola magnetycznego
c) ferromagnetyki - silnie wciągane do pola magnetycznego
Magnetyzacja
Średni moment magnetyczny liczony na jednostkę objętości:
![]()
ma t(w.) = z <me (w.)>
M(w.) = n ⋅ mat(w.) = n Z <me(w.)>
29. Częstość Larmora. Podatność magnetyczna. Względna przenikalność magnetyczna μ.
Twierdzenie Larmora dotyczy zależn. między momentem magn. i mom. pędu elektr. w atomie i mówi, że ruch elektr. w obecności słabego pola magn. jest zawsze złożeniem ruchu bez pola magn. i dodatkowo obrotu wokół osi pola z prędkością kątową ω.
Do tego również odp. 28 „Wektor namagnesowania ...”
30. Diamagnetyzm. Podatność magnetyczna diamagnetyków.
Bez pola magn. (B(w.) = 0) mw(w.) = 0
m(w.)
mw(w.) = 0 =>
-m(w.)
Po wstawieniu diamagnetyka do pola B(w.) nastąpi zmiana momentu magnetycznego atomu.
↓ Δm(w.)
=> -2Δm(w.) = mw(w.)
B(w.)
Δm
Włączenie pola magn. spowod. zaindukow. momentu magnetycznego skierowanego przeciwnie do pola magnetycznego.
Podatność magnetyczna
χ =(df.) = μ / H = Mμ0 / B
Względna przenikalność magnetyczna:
μ = χ + 1
Podatność magnetyczna diamagnetyków.
M(w.) = - n Z <Δm(w.)> ,
Δm(w.) = - e2 ri2 B(w.) / 4m*
ri2 = xi2 + yi2 (dla płaszcz. x,y)
Dla przestrzeni 3-wymiarowej:
r2 = x2 + y2 + z2 <r2> = <x2> + <y2> + <z2>
<x2> = <y2> = <z2> <r2> = 3 <x2>
<ri2> = 2<xi2> = 2 <r2>/3 <x2> = <r2>/3
<Δm(w.)> = e2<ri2>B / 4m*
<Δm(w.)> = e2<r2>B / 6m*
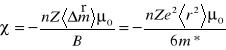
χ ∼ 105 0 < μ=1+χ < 1
31. Paramagnetyzm. Prawo Curie.
Paramagnetyki mają trwały moment magnetyczny m0(w.) nawet bez obecności zewnętrznego pola magnetycznego. Najczęściej mają nieparzystą liczbę elektronów na zewnętrznej powłoce. Po wstawieniu paramagnetyka do pola magn. występują w mim dwa procesy:
a) porządkowanie kierunków momentów magnetycz. atomowych zgodnie z kierunkiem zewnętrznego pola B. Procesowi temu przeszkadzają drgania cieplne atomów.
b) indukowanie się dodatkow. momentów magnetyczn. poprzez oddziaływanie z zewnętrznym polem B tak jak w diamagnetykach.
Drugi proces jest znacznie słabszy niż pierwszy.
Wektor magnetyzacji paramagnetyka.
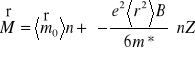
WB = - m0(w.) B <m0(w.)> = m02B / 3kT
Prawo Langevine'a - Courie
32. Ferromagnetyki. Pętla histerezy. Domeny ferromagnetyczne.
Ferromagnetyzm dotyczy tylko ciał stałych.
B∼Iind
H∼I
Pętla histerezy (wąska pętla - miękkie ferromagn. , szeroka pętla - twarde f.)
Budowa domenowa ferromagnetyków. (w jednej domenie identycznie ustawione momenty)
Efekt Berkhausena - drgania
33. Związek między wektorami B, H i M.
Trzy wektory magnetyczne (B(w.),H(w.),M(w.))
Z prawa Ampere'a
Pomiędzy M(w.) i IM można napisać związek:
←
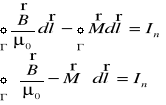
Dla para- i diamagnetyków B, H, M są współliniowe.
χ = M/H M = χ H
B = μ0H + μ0 χ H
B = μ0H (1+ χ) = μ0μH M = (μ - 1)H
nawias = μ
34. Zjawiska magnetomechaniczne. Doświadczenie Einsteina - de Haasa.
1. Efekt magnetostrykcji
Zmianie kształtu materiału magnetycznego pod wpływem zewnętrznego pola magnetycznego.
2. Doświadczenie E-dH - Richardsona (efekt)
/ / / / / / / /
m(w.) || I(w.)
Po zmianie wektora B(w.)
na przeciwny momenty
B(w.)↑ magnetyczne i momenty
pędu również zmienią
zwroty na przeciwne.
Z zasady zach. mom. pędu wynika, że walec powinien zacząć się obracać, aby całkowity mom. pędu uległ zmianie.
↑↓ -> g = czynnik Landego
35. Energia pola magnetycznego.
I WB= ½ LI2 , L= μ0n2V ; n=N/l - gęstość nawinięcia, V=S⋅l - obj. Solenoidu
WB= ½ μ0n2 V⋅ I2
WB= ½ μ0n2I2V= 1/ 2μ0 ⋅ μ02n2 I2V= 1/ 2μ0 ⋅ B2V (B=μ0nI)
Gęstość energii ωB= WB/V= B2/ 2μ0
ωB= B2/ 2μ0= ½ B(w.)/μ0 B(w.)=½ B(w.) ⋅ H
B(w.)= μ0H(w.) + μ0M(w.) =>
ωB= ½ (μ0H(w.) + μ0M(w.))H(w.) =
= ½ μ0H2 + ½ μ0M(w.)H(w.) = ½ B(w.)H(w.)+
gęst. w próżni gęst. + ½ B(w.)M(w.)
36. Prąd przewodzenia i przesunięcia. Pole elektromagnetyczne.
dΦE/dt - prąd przesunięcia.
Poprawione prawo Ampere'a:
37. Równania Maxwella w postaci całkowej i różniczkowej.
1. Postać całkowa
a) Prawo Gaussa dla E(w.)
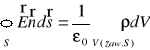
b) Prawo Gaussa dla pola B(w.)
![]()
c) Prawo Faraday'a
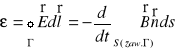
d) Uzupełnione prawo Ampere'a
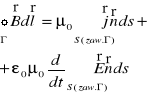
2. Postać różniczkowa
a) ∇E(w.) = ρ / ε0
b) ∇B(w.) = 0
c) ∇ × E(w.) = - ∂B(w.) / ∂t
d) ∇ × B(w.) = μ0 j(w.) + ε0 μ0 ∂E(w.) / ∂t
38. Fala elektromagnetyczna. Wektor Poyntinga.
Aby wytworzyć falę elektromagnetyczną, konieczny jest ruch przyspieszony ładunku.
Transport energii opisuje wektor Poyntinga s(w.) = 1/μ0 E(w.) × B(w.) [s]=[W / m2]
E(w.)
c→
k(w.)
B(w.)
C ≈ 300 000 km/s
39. Drgania harmoniczne: swobodne, tłumione i wymuszone (mechanicznie i elektrycznie).
Drgania harmoniczne - pod wpływem siły harmonicznej (k - st. spręż. , F = - kx ,
x - wychyl. z poz. równowagi)
odpychające
siła a
wypadkowa r
przyciągające
Wokół położenia r = a
F ≈ - k (r-a) - siła harmoniczna
1. Drgania harmoniczne swobodne (1-wym).
Siła harmoniczna Fn = -kx , równanie ruchu ma postać
Równanie może mieć postać: x(t) = A sin ⋅
⋅ (ω0t + ϕ)
War. początkowe: x(0) = x0 , x(.)(0) = x0(.) ,
x(.)(t) = Vn(t) = A ω0 cos (ω0t + ϕ)
x0 = A sin ϕ ∧ x0(.) = A ω0 cosϕ
trϕ = sinϕ / cosϕ = x0/A ⋅ Aω0/x0(.)
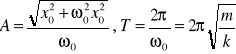
2. Oscylator harmoniczny tłumiony.
Ft = -γ Un = - γ x(.)
Fn = - k x Równanie ruchu ma postać
m x(..) = - kx - γx(.) || mx(..) + γx(.) + kx = 0
|| : m
x(..) + γ/m x(.) + k/m x = 0, γ/m = 2β, k/m = ω02
x(..) + 2β x(.) + ω02 x = 0
Możliwe rozwiązanie ma postać
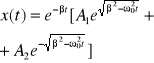
Rozważamy trzy przypadki:
a) ω02 > β2 - słabe tłumienie
b) ω02 = β2 - tłumienie kryt.
c) ω02 > β2 - silne tłumienie
3. Drgania wymuszne.
40. Składanie drgań. Dudnienia.
Składanie drgań prostopadłych.
/
/
/
/
/ / / / / / / / / / / / / / /
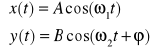
Dla pewnych szczególnych przypadków drgań:
1. A≠B , ω1=ω2=0 , ϕ=0
x = A cos(ωt) |=> y/x = B/A => y = B/A ⋅ x
y = B cos(ωt) |
2. A ≠ B , ω1=ω2=ω , ϕ = - π/2
| x = A cos(ωt)
| y = B cos(ωt - π/2)
y = B cos [ - (π/2 - ωt) ]
y = B cos (π/2 - ωt) = B sin ωt
x/A = cos (ωt) |
y/B = sin (ωt) |
x2/A2 + y2/B2 = cos2 (ωt) + sin2 (ωt)
x2/A2 + y2/B2 = 1 - elipsa
3. A≠B , ω1=ω2=ω , ϕ ≠ 0 , ϕ ≠ - π/2
4. A≠B , ω1≠ω2 , ϕ = 0
ω1 / ω2 = m/n m,n ∈ N (liczby naturalne)
- krzywe Lissajans
ω1 / ω2 = 2 / 1 ω1 / ω2 = 3 / 2
43. Współczynnik załamania. Związki dyspersyjne.
n =(df.) C/V V = C/n
1. Rozchodzenie się światła w dielektryku.
S P
z
E = E0 eiωt
Bez płytki szklanej fala w pkt. P ma postać E(P) = E0 eiω(t-z/c) (tam jest: iω(t-z/c))
Po wstawieniu płytki szklanej o grubości Δz , fala „opóźnia się” o Δt1 = Δz/V - Δz/c = Δzn/c - Δz/c = Δz/c ⋅ (n-1). W tej sytuacji fala w pkt. P ma postać E(P) = E0eiω(t-Δt-z/c) (tzn. iω(t-Δt-z/c))
E(P) = E0eiω[t-Δz/c ⋅ (n-1) -z/c]
(tzn. iω[t-Δz/c ⋅ (n-1) -z/c]
2. Natężenie pola elektrycznego od drgającego ładunku.
x0 Ex
r P
q E ∼ 1/r2
-x0
Ex= -q/ (4πε0c2r) ax (t-r/c)
Ex= 1/r
3. Pole elektryczne pochodzące od płaszczyzny drgających ładunków.
q - ładunek drgający
η - gęstość powierzchni
drgających ładunków
![]()
Vn prędkość harmoniczna
E(P) ∼ Vn
44. Doświadczenie Younga. Interferencja.
/
/
/
/
P
A
θ .
A θ
B
Δ = a sin θ
Warunek wzmocnienia z p. P
Δ = m λ ; m = 0, 1, 2, 3, ... ; a sin θ = m λ
Warunek wygaszenia w p. P
Δ = (ηm + 1) λ / 2 ; a sin θ = (ηm + 1) λ / 2
ϕ / 2π = Δ / λ
Natężenie w doświadczeniu Younga.
Równania fal ze źródeł A i B mogą mieć w p. P postać: | EA = E0 sin (ωt)
| EB = E0 sin (ωt + ϕ)
Fala wypadkowa ma postać:
Ew(P) = EA + EB = E0 [sin(ωt) + sin(ωt + ϕ)]
Ew = 2E0 cosϕ/2 sin (ωt + ϕ/2)
Natężenie fali A lub B I0 ∼ E02
Natężenie fali wypadk. Iw ∼ E'2
Iw / I0 = E'2 / E02 =>
Iw = Iα E'2 / E02 = 4 I0 cos2δ δ = ϕ/2
ϕ/2π = Δ/λ => ϕ = 2πΔ / λ => δ = ϕ/2 = πΔ/λ
Iw = Imax , gdy cos2δ = cos2 ϕ/2 = 1 => ϕ/2 = mπ (m=0,1,2,…)
Stąd πΔ / λ = mπ a sinθ / λ = m
a sinθ = m λ
Iw = 0 , gdy cos2δ = cos2ϕ/2 = 0 =>
ϕ/2 = (2m - π)π/2
πΔ / λ = (2m + 1)π/2
a sinθ / λ = (2m + 1) ½
a sinθ = (2m + 1) λ/2
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
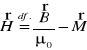
![]()
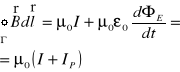
Wyszukiwarka
Podobne podstrony:
fiz odp2 1 , Fizyka 2
303b, Studia, ROK I, 1 semestr, Fizyka, LABKI z FIZ, Sprawozdania, fizyka lab sprawka, Fizyka- labor
Wyznaczanie współczynnika przewodnictwa cieplnego metali, FIZ-106, Fizyka 106
Wyznaczanie współczynnika przewodnictwa cieplnego metali, FIZ-106, Fizyka 106
302A, Studia, ROK I, 1 semestr, Fizyka, LABKI z FIZ, Sprawozdania, fizyka lab sprawka, Fizyka- labor
309pio1, Studia, ROK I, 1 semestr, Fizyka, LABKI z FIZ, Sprawozdania, fizyka lab sprawka, Fizyka- la
FIZ 7 K2, fizyka lab, 07
109pio2, Studia, ROK I, 1 semestr, Fizyka, LABKI z FIZ, Sprawozdania, fizyka lab sprawka, Fizyka- la
109pio1, Studia, ROK I, 1 semestr, Fizyka, LABKI z FIZ, Sprawozdania, fizyka lab sprawka, Fizyka- la
Zestaw Fiz.wsp, AGH, ROK I, fizyka, Fizyka
Lab fiz 43 2, Studia, Semestr 1, Fizyka, Sprawozdania
Nr ćwiczenia5 moje, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, labor
Fiz 10 P, Studia, Ogólne, Fiyzka, od romka, studia materiały, Fizyka lab, Termopary
fiz odp na pyt grA i B, Politechnika Poznańska, ZiIP, Semestr I, Fizyka
więcej podobnych podstron