MATLAB

Podstawy

help help - lista słów kluczowych

help słowo_kluczowe - opis znaczenia słowa kluczowego

demo - wykonanie polecenia zewnętrznego demo.m

exit - wyjście z MATLABa

quit - j.w.

Macierze - sposoby tworzenia i zapisu

Jedynym typem obiektu w MATLABie jest macierz prostokątna . W szczególności macierze mogą być wektorami - wierszami lub kolumnami albo skalarami. Macierze mogą być tworzone poprzez

• wprowadzanie bezpośrednio z klawiatury,

• wczytanie pliku .m ze zdefiniowaną macierzą,

• wygenerowanie przez funkcję,

• załadowanie z pliku zewnętrznego .mat.

Macierze - sposoby notacji

Spacja oddziela elementy wiersza, średnik oddziela wiersze

A = [ 1 2 3; 4 5 6; 7 8 9 ]

Przecinek też oddziela elementy wiersza

A = [ 1, 2, 3; 4, 5, 6; 7, 8, 9 ]

ENTER też oddziela wiersze

A = [ 1 2 3

4 5 6

7 8 9 ]

Zauważmy, że nie potrzeba deklarować rozmiaru macierzy.

A = [ X Y; Z ] - oznacza macierz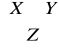
, wymiary muszą się zgadzać.

A = [ A; [ 10 11 12 ] ] - dodaje do A wiersz [ 10 11 12 ]

A = [] - przyporządkowuje A macierz pustą

A(1, 2) - odwołanie do elementu macierzy o indeksie (1, 2)

Jeśli A = [ 1 2 ], to przypisanie A(5) = 5 spowoduje odpowiednie zwiększenie wymiaru A i uzupełnienie zerami: A = [ 1 2 0 0 5 ].

Używanie dwukropka

A = J:K - wektor-wiersz z liczbami od J do K, pusty, jeśli J > K (dwukropek oznacza tu “od - do”)

A = J:I:K - wektor-wiersz z liczbami od J do K z przyrostem I (przyrost może być do-datni lub ujemny)

A(:,J) - J-ta kolumna A (dwukropek oznacza tu “wszystkie indeksy”)

A(1:5,3) - macierz wymiaru 5x1 utworzona z pierwszych pięciu elementów trzeciej kolumny A.

Załóżmy, że A ma wymiar nxn:

A(1:5,n-3:n) - macierz 5x4 utworzona z pierwszych pięciu wierszy ostatnich czterech kolumn.

A(1:5,:) - pierwszych pięć wierszy macierzy A.

Ogólnie, jeśli v, w - wektory o składowych całkowitych, to A(v, w) oznacza macierz o elementach A z wierszy o indeksach równych kolejnym składowym wektora v, (tzn. po-numerowanych według wektora v) i z kolumn ponumerowanych według elementów we-ktora w.

Przykłady:

A(: ,n:-1:1) - przestawia kolumny A

A(:, [ 3 5 10 ]) = B(:,1:3) - zamienia trzecią, piątą i dziesiątą kolumnę A pierwszymi trzema kolumnami B.

A([ 1,5 ],:) = A([ 5, 1 ],:) - wymienia wiersz pierwszy z piątym macierzy A

A(:,[ 2 4 ]) = [] - usuwa drugą i czwartą kolumnę z macierzy A

B = A(:) - wszystkie elementy A układane są w jeden wektor kolumnowy B

A(:) = B - operacja odwrotna, B jest wektorem-kolumną, macierz A (musi wcześniej istnieć) wypełnia się elementami B.

Używanie wektorów zero-jedynkowych

Jeżeli L jest wektorem długości m o elementach zero lub jeden, A - macierzą wymiaru nxn, to A(L,:) wybiera wiersze A o numerach, dla których składowa L jest różna od 0.

Macierze o elementach zespolonych

Należy najpierw zdefiniować jednostkę urojoną, np.

i = sqrt(-1)

a następnie można tworzyć macierze zespolone, np.

A = [ 1 2; 3 4 ] + i*[ 5 6; 7 8 ]

lub

A = [ 1+5*i 2+6*i; 3+7*i 4+8*i ]

(uwaga na spacje!).

Elementarne operacje i funkcje na macierzach

A+B - dodawanie, macierze muszą mieć te same wymiary. Jeżeli jednym z operandów jest skalar, to jest dodawany do wszystkich elementów macierzy.

Analogiczne zasady obowiązują dla:

A-B - odejmowania

A*B - mnożenia

A' - transponowanie (z zamianą elementów na sprzężone)

Potęgowanie

Operacje potęgowania to:

A^p oraz p^A (A - macierz kwadratowa, p-skalar)

Dzielenie

A\B = inv(A)*B - jeśli A kwadratowa i nieosobliwa

B/A = B*inv(A) - A kwadratowa i nieosobliwa

Obliczanie wykonywane jest bez odwracania przez rozwiązanie układu A*X = B lub X*A = B. A\B jest wiec określone jeśli B ma tyle wierszy co A. Jeśli A jest kwadratowa, używana jest metoda eliminacji Gaussa z odpowiednim komunikatem w przypadku osobliwości A. Jeśli A prostokątna, używana jest metoda najmniejszych kwadratów do “rozwiązania” odpowied-niego układu równań. Wynikiem jest macierz X wymiaru mxn, gdzie m - liczba wierszy A, n - liczba kolumn B.

B/A = (A'\B')'

Operacje typu element-element

Poprzedzając symbol operacji kropką “.” zamieniamy ją na operację typu “element-element”:

A .* B - A i B tego samego wymiaru, mnożenie odbywa się metodą “element A * odpowiedni element B”

A .\ B, A ./ B - dzielenie

A .^ B - potęgowanie, np. 2 .^ [ 1 2 3 4 ] daje wektor [ 2 4 8 16 ]. Uwaga: ważna jest spacja po “2” aby odróżnić “.^” od “2.”

A .' - transponowanie bez sprzęgania.

Operacje porównań

A < B - porównuje pary elementów macierzy A i macierzy B (tych samych wymiarów) dając w wyniku macierz 0-1 (0 - fałsz, 1 - prawda ). Można dokonywać porównań przy użyciu operatorów: <=, >, >=, ==, ~=, (~ - not).

Przykład: eliminacja z wektora X elementów przekraczających trzykrotne odchylenie standardowe:

X = X(X <= 3*std(X))

(patrz również usuwanie wektorów zero-jedynkowych).

Operacje logiczne

Do dyspozycji mamy trzy operatory logiczne:

& - and, | - or, ~ - not.

Działając na kolejnych parach elementów macierzy A oraz B zwracają macierz zero-jedynkową będącą wynikiem danej operacji logicznej (jako TRUE traktowana jest każda liczba różna od zera).

Przykłady:

A | (~A) - macierz “jedynek”

A &(~A) - macierz “zer”.

Teksty

Instrukcja

s = `Hello'

daje w wyniku wektor-wiersz s pamiętany jako kody ASCII poszczególnych liter. Jest traktowany jako normalny wektor, z tym że podczas wyświetlania instrukcją disp pokazują się litery zamiast liczb. Z każdą zmienna związany jest bowiem indeks mówiący, czy ma być wyświetlana jako tekst czy liczba.

t = abs(s) powoduje zmianę indeksu w ten sposób, że wektor t będzie wyświetlany jako liczby (kody ASCII).

t = setstr(t) zamienia indeks z powrotem na tekstowy.

isstr(t) = 1 jeśli t jest tekstem, 0 w przeciwnym przypadku.

t = num2str(x) zamienia skalar x na jego tekstową reprezentację, ok. 4 cyfry po przecinku, wygodne do etykietowania osi.

t = sprintf(`format', x, y, z) - bezpośrednia kontrola nad formatem wyjściowym tekstu t. Specyfikatory formatu: %d %e, %f, %g. Działa podobnie do analogicznej funkcji języka C.

fprintf - jak sprintf z tym, że wyjściem może być plik:

fprintf(`nazwa_pliku', `format', x, y, z)

Obliczanie wyrażeń wewnątrz tekstów

eval(t) obliczany lub wykonywany jest tekst t, np. t = `1/(i+j)',używane do przekazywania nazw w plikach .m.

feval - jeśli f jest łańcuchem - nazwą funkcji, to feval(f,x1,...,xn) oblicza ją dla danych argumentów. Używane zwykle wewnątrz funkcji mających nazwy innych funkcji jako argumenty.

Zmienne

Typowa instrukcja MATLABa ma postać

zmienna = wyrażenie

lub po prostu

wyrażenie

• obliczenie wyrażenia produkuje macierz - jest ona wyświetlana i przypisywana zmiennej. Jeśli brak przypisania, tworzona jest automatycznie zmienna ans z wartością wyrażenia.

• Instrukcja wykonywana jest po ENTER. Jeśli zakończono ją średnikiem `;', to nie jest wyświetlana na ekranie.

• Jeśli instrukcja nie mieści się w linii, to przeniesienie do następnej linii odbywa się przy pomocy …, np.

X = 1 + 1/2 + 1/3 + … (ENTER)

1/4 + 1/5

• Małe i duże litery są odróżniane (np. nazwy funkcji zewnętrznych są pisane małymi literami). Komenda casesen przełącza ten tryb.

• Zakres liczb: 10^-308 - 10³⁰⁸.

• Element macierzy rzeczywistej zajmuje 8 bajtów.

Zmienne predefiniowane

eps - wartość początkowa = odległość od 1 do największej najbliższej liczby zmienno-przecinkowej.

pi = 4*atan(1)

inf - “nieskończoność”, np. w wyniku przypisania x = 1/0 program nie jest przerywany, wyświetlany jest jedynie komunikat o dzieleniu przez 0, natomiast zmienna x przybiera wartość inf. W trakcie dalszych operacji ze zmienną x program zachowuje się “rozsądnie”, np. 1/x daje zero.

nan - “not a number” - wartość przypisywana w wyniku operacji typu 0/0 inf/inf. Jeśli gdzieś w środku obliczeń jest zmienna o wartości nan, to wynik końcowy jest też nan., chyba że nie zależy on od tej zmiennej.

Wyświetlanie macierzy

disp(A) wyświetla macierz A w postaci określonej przez format. Jeśli elementy macierzy są całkowite to wyświetlane są bez kropki. Jeśli co najmniej jeden element nie jest całkowity, to określić można jeden z następujących rodzajów formatów:

format short - 1.1234

format short e - 1.1234E+000

format long - 1.123456789012345E+000

format hex - format szesnastkowy

format bank - 1.12

format compact - mniej spacji między elementami macierzy

format + - elementy macierzy w postaci +/0/- (w zależności od znaku)

format - oznacza format short (jest to format domyślny).

cla - czyszczenie ekranu tekstowego

home - kursor na początek ekranu

Wybrane funkcje biblioteki MATLABa

[ m,n ] = size(X) - zwraca wymiar macierzy X

length(X) - zwraca długość wektora X, równoważne z max(size(X))

max - dla wektorów max(X) jest największym elementem X, dla macierzy , max(X) jest wektorem-wierszem z maksymalnymi elementami z kolumn tej macierzy.

[ Y, l ] = max(X) - zwraca również indeksy maksymalnych wartości

max(A, B) - zwraca macierz rozmiarów takich jak A i B z maksymalnymi elementami z obu

min - analogicznie do max.

Badanie elementów macierzy

all - dla wektorów , all(v) zwraca 1, jeśli wszystkie elementy są niezerowe, w prze-ciwnym razie zwraca 0. Dla macierzy operuje na kolumnach i zwraca wektor-wiersz 0-1.

any - zwraca 1, jeśli istnieje element różny od 0; zasady dla wektora i macierzy analogiczne jak dla all.

Na przykład

any(any(A))

daje w rezultacie 1, jeśli wszystkie elementy macierzy są niezerowe. Powyższe funkcje są użyteczne w instrukcjach warunkowych np.

if all( A < .5 )

instrukcje MATLABa

end

find(K) - zwraca indeksy wektora K elementów różnych od zera.

finite - sprawdzenie skończoności elementów macierzy.

isempty - służy do wykrywania pustej macierzy

isstr - sprawdza czy zmienna jest łańcuchem tekstowym

isnan - testuje istnienie zmiennej nan w macierzy.

Podstawowe wielkości charakteryzujące macierz

det(X) - jest wyznacznikiem macierzy kwadratowej

inv(X) - odwracanie macierzy kwadratowej

cond(X) - miara wrażliwości rozwiązania układu równań liniowych na błędy danych. Daje wskazówkę co do dokładności wyników otrzymanych podczas odwracania macierzy i rozwiązywania układów równań.

rank - rząd macierzy

eig - wektory i wartości własne: A*x = lambda*x, A - nxn; eig(A) - wektor z warto-ściami własnymi [ X, D ] = eig(A) - D jest macierzą z wartościami własnymi na przekątnej; kolumny X odpowiadają wektorom własnym, A*X=X*D.

Przekształcanie macierzy

diag - jeśli V jest wektorem o n składowych, to diag(V,k) oznacza macierz kwadratową rzędu n+abs(k) z elementami wektora V ustawionymi na k-tej przekątnej, k=0 - na głównej, k > 0 - powyżej,, k < 0 - poniżej.

diag(V) - ustawia te elementy na głównej przekątnej . Jeśli X jest macierzą, diag(X,k) jest wektorem-kolumną utworzonym z elementów głównej przekątnej.

diag(X,k) - jest wektorem-kolumną utworzonym z elementów k-tej przekątnej X. diag(X) wektor-kolumna utworzona z elementów głównej przekątnej.

triu(X) - macierz trójkątna górna utworzona z macierzy X.

tril(X) - macierz trójkątna dolna, zasady analogiczne

Funkcje wykonywane na poszczególnych elementach macierzy

abs - moduł (obliczany też dla macierzy o elementach zespolonych)

real - część rzeczywista

imag - część urojona

conj - sprzężenie

exp - funkcja wykładnicza (obliczana też dla macierzy zespolonych)

log - logarytm naturalny

log10 - logarytm dziesiętny

sin, cos, tan - funkcje trygonometryczne (macierze mogą być zespolone).

asin, acos, atan - funkcje odwrotne do trygonometrycznych

sinh, cosh, tanh - funkcje hiperboliczne

sign(A) - macierz o elementach 1/0/-1; dla zespolonych A sign(A) = A ./ abs(A)

Funkcje do zaokrąglania

round - do najbliższej całkowitej

fix - do najbliższej całkowitej w kierunku zera.

ceil - do najbliższej całkowitej w prawo

floor - do najbliższej całkowitej w lewo

rem - jeśli n=fix(x/y) to rem(x,y)=x-y*n (reszta z dzielenia)

Funkcje uogólnione

Normalnie wyrażenia typu exp(A) są wykonywane na poszczególnych elementach macierzy A. Na macierzach kwadratowych możliwe jest wykonywanie funkcji uogólnionych. Funkcja jest traktowana jako uogólniona, jeśli na końcu jej nazwy znajduje się litera “m”, np. expm, logm, sqrtm.

Generatory liczb losowych

rand(n) - macierz nxn o wartościach losowych wg rozkładu jednostajnego z przedziału [0, 1].

rand(m,n) - macierz mxn

rand(A) -ten sam wymiar co A

rand -skalar

rand(`normal') - przełącza generator na rozkład normalny N(0,1).

rand(`uniform') - powrót do rozkładu jednostajnego na odcinku [0, 1]

rand(`seed') - zwraca bieżącą wartość ziarna generatora.

rand(`seed', n) - ustawia ziarno na n. Przy włączeniu jest n = 0.

Użyteczne macierze

ones(n) - macierz nxn utworzona z samych jedynek

ones(m,n) - j.w. - wymiaru mxn

ones(A) - wymiaru takiego jak macierz A, chyba że A jest skalarem

zeros(n) - macierz wymiaru nxn utworzona z samych zer.

zeros(m,n) - macierz mxn utworzona z samych zer

zeros(A) - wymiaru takiego jak macierz A, chyba że A jest skalarem

eye(n) -macierz jednostkowa wymiaru nxn

magic(n) - macierz nxn utworzona z liczb całkowitych od 1 do n*n o równych sumach wierszy i kolumn.

Zarządzanie zmiennymi

who - podaje nazwy istniejących w pamięci zmiennych oraz nazwy czterech prede-finiowanych zmiennych: eps, pi, inf, nan.

whos - lista zmiennych wraz ze stanem pamięci

exist(`A') - zwraca 1 jeśli A jest zmienną , 2 - plikiem tekstowym z rozszerzeniem .m, 0 - jeśli A nie istnieje

pack - optymalizuje wykorzystanie pamięci operacyjnej : wszystkie zmienne zapisywane są na plik pack.tmp i wczytane od nowa. Używana po komunikacie “Out of memory”

clear - usuwa wszystkie zmienne i funkcje

clear X - usuwa zmienną X

clear functions - usuwa wszystkie skompilowane funkcje.

casesen - przełącza rozróżnianie dużych i małych liter, standardowo są rozróżniane.

Zapisywanie zmiennych do pliku

save temp A - powoduje zapisanie na pliku temp.mat zmiennej A (w formacie MATLABa)

save temp A B C - zapisanie zmiennych A, B i C.

save - zapisanie wszystkich zmiennych z pamięci do pliku matlab.mat

load temp - wczytanie zmiennych zapisanych w pliku temp.mat

load - wczytanie zmiennych zapisanych w pliku matlab.mat.

load plik ASCII - powoduje utworzenie zmiennej o nazwie pliku

what - wyświetla listę plików z bieżącego katalogu z rozszerzeniem .mat.

Wprowadzanie danych z klawiatury

input(`podaj liczbę') - wyświetla tekst „podaj liczbę” na ekranie i oczekuje na wprowa-dzenie danych z klawiatury. Dana ta jest wartością funkcji input.

input(`podaj nazwę', 's') - oczekuje na wprowadzenie tekstu przypisywanego zmiennej łańcuchowej s.

keyboard - instrukcja ta umieszczona w makropoleceniu, przełącza kontrolę na klawiaturę, tzn. traktuje klawiaturę jako plik .m. Można zmieniać wówczas np. wartości zmiennych i je wyświetlać (ułatwia testowanie makropoleceń). Powrót do makropolecenia następuje po wprowadzeniu CTRL-Z.

Funkcje o wielu argumentach i wartościach

Funkcje mogą zwracać więcej niż jedną wartość, jednak można je wywoływać biorąc tylko jedną wartość wyjściową, np. [ V, D ] = eig(A) - funkcja zwracająca dwie wartości, V = eig(A) - wywołanie tej funkcji z jedną wartością wyjściową. Przy definiowaniu funkcji do obliczania ilości wartości wyjściowych z jaką nastąpiło jej wywołanie służy funkcja nargout. Podobnie można definiować funkcje działające na mniejszej niż w nagłówku ilości argumentów wejściowych. Liczba argumentów, z jaką wywołana została funkcja, podawana jest przez nargin.

Grafika w MATLABIE

Rysowanie wykresu x-y

plot(Y)

• Jeśli Y jest wektorem, to plot(Y) rysuje elementy wektora Y względem jego indeksów i interpoluje liniowo

• Jeśli Y jest macierzą, to plot(Y) rysuje elementy kolumn względem indeksów (będziemy więc mieć tyle linii ile jest kolumn macierzy).

• Jeśli Y jest zespolone, to plot(Y) = plot(real(Y),imag(Y)). We wszystkich innych przypadkach rysowanie części urojonej jest ignorowane.

plot(X, Y)

• Jeśli X jest wektorem i Y jest wektorem, to rysowane są elementy Y względem elementów X.

• Jeśli X i Y są macierzami, to kolumny Y są rysowane względem kolumn X.

• plot(X1,Y1,X2,Y2) - inny sposób rysowania wielu wykresów: Y1 względem X1 i Y2 względem X2.

• plot(X,Y,'o'), plot(X1, Y1, `+', X2,Y2, `*') - rysowanie z określeniem rodzaju linii

Mamy następujące rodzaje linii: -, --, :, -., ., +, o, x.

Możliwe jest sporządzanie wykresów w innych układach współrzędnych. Zasady przekazy-wania parametrów do funkcji są takie same jak dla plot.

polar(theta, rho) - wykres we współrzędnych biegunowych, gdzie theta oznacza kąt, a rho promień wodzący.

semilogx(X, Y) - oś odciętych w skali logarytmicznej.

semilogy(X, Y) - oś rzędnych w skali logarytmicznej.

loglog(x, y) - obie osie w skali logarytmicznej.

Opisywanie osi wykresów x-y

title(`tekst') - wyprowadza tekst nad wykresem

xlabel(`tekst') - opis osi x

ylabel(`tekst') - opis osi y

text(x, y, `tekst') - umieszcza tekst w punkcie (x, y) ekranu graficznego, przy czym punkt (0.0, 0.0) oznacza lewy dolny róg ekranu.

grid - nanoszenie siatki.

Ręczne skalowanie osi

axis - wyłącza automatyczne skalowanie, ponowne axis włącza. Funkcja ta zwraca wektor [ xmin, xmax, ymin, ymax ] z zakresami osi odciętych i rzędnych ostatniego rysunku..

axis(V) - gdzie V jest wektorem o czterech składowych, skaluje osi według wektora V.

axis(`square') - instrukcja powoduje, że skale osi odciętych i rzędnych są identyczne (np. rysunek koła jest wówczas bez zniekształceń); axis(`normal') wyłącza tę opcje.

Zarządzanie ekranem

hold - zatrzymuje bieżący wykres na ekranie, następne są rysowane bez wyczyszczenia poprzedniego ekranu. Obowiązuje do następnego użycia.

shg - przełączanie z ekranu tekstowego na graficzny.

cla - czyszczenie ekranu tekstowego

clg - czyszczenie ekranu graficznego

Rysowanie wykresów w podoknach

subplot(mnp) - gdzie mnp liczba trzycyfrowa, dzieli ekran na mxn podokien jednakowej wielkości i wybiera p-te do rysowania tzn. następny wykres będzie rysowany w p-tym podoknie, kolejny w p+1-szym).

Rysunki wykresów trójwymiarowych

mesh(Z) - trójwymiarowy obraz macierzy Z.

mesh(Z,M) - (gdzie M = [ az, el ]) definiuje punkt widzenia powierzchni, az jest azy-mutem, a el elewacją pionową.

mesh(Z, M, S) - (gdzie S = [ sx, sy,sz ]) określa dodatkowo współczynniki sx, sy, sz do ska-lowania osi.

meshdom - funkcja wykorzystywana do przygotowywania macierzy Z, którą chcemy na-rysować używając polecenia mesh.

Przykład: rysowanie trójwymiarowego wykresu funkcji z = x*exp(-x²- y²):

[ x, y ] = meshdom(-2:.2:2, -2:.2:3);

z = x .* exp(-x .*x - y .*y);

mesh(z)

contour - rysowanie warstwic.

Język programowania MATLABa

Instrukcje sterujące

MATLAB posiada zestaw instrukcji sterujących, które działają podobnie jak analogiczne in-strukcje w językach wysokiego poziomu, takich jak Pascal czy C.

Pęta for

Pętlę for stosujemy jeśli znamy ilość razy jaką pętla ma się wykonać. Ogólna postać pętli for jest następująca:

for v = wyrażenie

lista instrukcji

end

wyrażenie jest na ogół macierzą, której kolumny są wyliczane kolejno w czasie wykonywania pętli. Powyższa pętla mogłaby być zapisana nieco przejrzyściej jako:

w = wyrażenie;

[ m, n ] = size(w);

for j = 1:n

v = w(:,j);

lista instrukcji

end

Każda pętla musi być zakończona słowem kluczowym end. Pętle można zagnieżdżać. Na przykład pętla:

for i = 1:n, x(i) = 0, end

wyzeruje n pierwszych elementów wektora x. Jeśli n < 1 instrukcje w obrębie pętli nie wy-konają się ani razu. Jeśli x nie istnieje lub ma mniej niż n elementów, to rozmiar wektora zostanie automatycznie rozszerzony.

Przy zagnieżdżaniu pętli dobrze jest stosować wcięcia by polepszyć czytelność:

for i = 1:m

for j = i:n

A(i,j) = 1/(i + j - 1);

end

end

Dwukropek na końcu instrukcji wewnątrz pętli zapobiega wielokrotnemu drukowaniu wy-niku.

Przykład:

Załóżmy, że t = [ -1 0 1 3 5 ]' i chcemy wyznaczyć macierz, której kolumny są potęgami elementów wektora kolumnowego t.

n = max(size(t));

for j = 1:n

for i = i:n

A(i,j) = t(i)^(n-j);

end

end

Można to zadanie rozwiązać w sposób bardziej zwarty, i jak się okazuje, efektywniejszy.

A(:,n) = ones(n,1);

for j = n-1:-1:1

A(:,j) = t .* A(:,j+1);

end

Pętla while

Pętlę while stosujemy, jeśli nie znamy z góry liczby iteracji pętli. Pętla ma następującą ogólną postać:

while wyrażenie

lista instrukcji

end

wyrażenie daje w wyniku macierz. lista instrukcji jest powtarzana, dopóki macierz wynikowa wyrażenia warunkowego ma wszystkie elementy różne od zera.

Przykład:

Jaka jest najmniejsza liczba całkowita, której silnia jest liczbą 100 - cyfrową.

n = 1;

while prod(1:n) < 1.e100

n = n + 1;

end

n

Kolejny przykład wyznacza exp(A) jako sumę szeregu:

E = zeros(A);

F = eye(A);

k = 1;

eps = 0.001;

while norm(F,1) > eps

E = E + F;

F = A*F/k;

k = k + 1;

end

E

Jeśli chcielibyśmy wyznaczyć macierz eksponent o wykładnikach równych elementom ma-cierzy, to w powyższym programie wystarczyłoby zmienić inicjację macierzy F na F = ones(A) oraz mnożenie macierzowe A *F na mnożenie typu element-element A .* F.

Instrukcja warunkowa if oraz instrukcja break

Przykład:

if n < 0

A = negative(n);

elseif rem(n, 2);

A = even(n);

else

A = odd(n);

end

A

W powyższym przykładzie sterowanie obejmuje trzy przypadki w zależności od znaku i parzystości zmiennej n.

Instrukcja break powoduje przerwanie wykonania pętli i przejście do instrukcji występującej bezpośrednio za pętlą. W poniższym przykładzie program wymaga wprowadzenia dodatniej liczby z klawiatury w nieskończonej pętli. Wprowadzenie liczby ujemnej przerywa wykonanie pętli.

while 1

n = input(`Wprowadz n > 0, n <= 0 konczy zadanie ');

if n <= 0, break, end

while n > 1

if rem(n, 2) == 0

n = n/2

else

n = 3*n + 1

end;

end

end

Pisanie własnych skryptów i funkcji

MATLAB może być używany w trybie interakcyjnym zachowując się jak kalkulator macierzowy. Pojedyncze komendy wprowadzane z klawiatury są natychmiast przetwarzane, a rezultaty wyprowadzane na ekran. MATLAB może również wykonywać sekwencje komend zawarte w plikach tekstowych z rozszerzeniem .m zwane M-plikami. Wprowadzając nazwę takiego pliku powodujemy wykonanie sekwencji komend w nim zawartych. M-pliki mogą zawierać, oprócz standardowych poleceń MATLABa, także wywołania innych M-plików lub rekurencyjne odwołania do samych siebie. M-pliki usprawniają pracę pozwalając na wy-woływanie długich sekwencji komend przez wprowadzenie jednej nazwy.

Mamy dwa rodzaje M-plików

• pliki skryptowe (lub po prostu skrypty)

• pliki funkcyjne

Pliki skryptowe

Pliki skryptowe zawierają sekwencje poleceń MATLABA (w tym odwołania do innych pli-ków skryptowych i funkcyjnych). Polecenia w skryptach operują na zmiennych globalnych w przestrzeni roboczej MATLABA. Przykładem skryptu jest polecenie demo, które wykonuje sekwencję poleceń z pliku demo.m.

Przykład skryptu obliczającego kilkanaście pierwszych liczb Fibonacciego i rysującego wykres:

% M-plik obiczajacy liczby Fibonacciego

f = [ 1 1 ]; i = 1;

while f(i) + f(i+1) < 1000

f(i+2) = f(i) + f(i+1);

i = i + 1;

end

plot(f)

Znak `%' w linii oznacza komentarz i powoduje że ciąg znaków za nim jest ignorowany przez interpreter. Komentarz rozciąga się od znaku procenta do końca linii.

Pliki funkcyjne

Pierwsza linia pliku zawiera słowo kluczowe function. Pliki funkcyjne różnią się od skrypto-wych możliwością przekazywania argumentów, a wszelkie zmienne definiowane w takim pliku są lokalne i nie są dostępne w globalnej przestrzeni roboczej MATLABa po zakończe-niu wykonania funkcji.

Przykład:

function y = mean(x);

% mean - wyznaczenie wartości średniej

% Jeśli argument jest wektorem - zwraca wartość średnia

% Dla macierzy - zwraca wektor wierszowy ze średnimi

% z poszczególnych kolumn macierzy

[ m, n ] = size(x)

if m == 1

m = n;

end

y = sum(x) / m

Można teraz używać komendy mean tak jakby była standardową komendą.

x = 1:99;

mean(x)

---