CIEPŁO

Wstęp

Pojęcie ciepła wiąże się nieodłącznie z pojęciem temperatury. Procesy związane z ciepłem są przedmiotem badań działów fizyki nazywanych fizyką cząsteczkową lub fizyką statystyczną oraz termodynamiką.

Termodynamika stosuje metodę opisu fenomenologiczną, opartą bezpośrednio na danych doświadczalnych i bada jedynie makroskopowe zjawiska, nie interesując się ich obrazem mikroskopowym. Podstawą termodynamiki są zasady termodynamiki.

Fizyka cząsteczkowa bada budowę i własności materii; posługuje się pojęciami teorii kinetyczno - molekularnej i stosuje opis statystyczny ruchu zbioru dużej liczby drobin.

Termodynamika i fizyka statystyczna uzupełniają się wzajemnie, wiążą ze sobą wielkości (obrazy) - makroskopowe i mikroskopowe procesów cieplnych.

Dynamika procesów cieplnych jest bardzo skomplikowana, stąd też wszystkie ilościowe rozważania termodynamiki dotyczą stanów równowagi układów i procesów odwracalnych.

Przez stan równowagi termodynamicznej (cieplnej) rozumiemy taki stan, w którym układ może pozostawać dowolnie długo a wszystkie parametry stanu (np. ciśnienie, objętość, temperatura, ......) mają określone wartości i nie ulegają zmianie.

Przez proces odwracalny, in. nazywany przemianą równowagową lub kwazistatyczną rozumie się taki proces, który składa się z ciągłego zbioru kolejnych stanów równowagi. Realne przemiany mogą być uważane za odwracalne, jeśli zachodzą dostatecznie powoli.

Jednym z podstawowych pojęć termodynamicznych jest wielkość zw. energią wewnętrzną ciała, zwykle oznaczana U . Jest to całkowita energia, jaką posiada ciało (kinetyczna i potencjalna oddziaływań wewnętrznych) z wyłączeniem energii kinetycznej i potencjalnej ciała wynikających z oddziaływań zewnętrznych pól.

Energia wewnętrzna - mówimy - jest funkcją stanu układu, tzn. ma zawsze tę samą wartość w danym stanie, niezależnie od „historii” układu.

Temperatura

Temperatura jest jednym z tzw. parametrów stanu i jest także funkcją stanu. Dwa ciała mają tę samą temperaturę, jeśli między nimi nie ma przekazywania ciepła.

Do określenia temperatury stosuje się powszechnie termometry, które są w sposób umowny skalowane. Używane są różne skale termometryczne. Najbardziej rozpowszechnione jest stosowanie skali Celsjusza, która polega na przyjęciu, że:

• w warunkach ciśnienia 1 atm - temperatura topnienia lodu wynosi 0 ⁰C, a wrzenia wody 100 ⁰C,

• wybrana tzw. cecha termometryczna (np. rozszerzalność objętościowa rtęci) zależy liniowo od temperatury.

W podobny sposób skalowane termometry, w szczególności dla różnych zakresów temperatur, zależą od własności użytych ciał termometrycznych i dlatego mogą posiadać de facto różne skale termometryczne.

II zasada termodynamiki pozwoliła dopiero zbudować skalę , która nie posiada wspomnianej wady. Nosi ona nazwę bezwzględnej termodynamicznej skali temperatur .

Jednostką temperatury bezwzględnej jest 1 K (kelwin) = 1 ⁰C.

Pomiędzy skalą Kelwina i skalą Celsjusza zachodzi związek

T = t +273,15

gdzie: T - temperatura w skali bezwzględnej; t - w skali Celsjusza.

Równanie stanu gazu doskonałego

Najprostszą do opisu termodynamicznego formą materii jest jej stan gazowy. Badania przeprowadzone dla różnych gazów pokazują jednak, że ich zachowanie w zależności od temperatury i ciśnienia są nieco różne, przy czym praktycznie brak różnic występuje dla gazów dostatecznie rozrzedzonych. Dlatego w termodynamice wprowadzono pojęcie tzw. gazu doskonałego o cechach charakterystycznych dla gazów rozrzedzonych o niewielkich gęstościach.

Doświadczenia pokazują, że dla ustalonej ilości (tej samej liczby drobin) takich gazów jest spełnione równanie

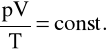
gdzie: p - ciśnienie gazu, V - jego objętość, T - jego temperatura.

W szczególności (prawo Avogadro) 1 mol każdego gazu zawiera zawsze tę samą liczbę drobin N_A =6,022 x 10²³ i zajmuje te samą objętość V_m zw. objętością molową. Stąd wynika, że dla 1 mola, stała występująca w podanym wzorze posiada określoną wartość; stałą tę przyjęto oznaczać symbolem R i z danych doświadczalnych wynika jej wartość

R = 8,31 J/(mol K)

Tak więc równanie wyżej podane, dla 1 mola może być przepisane w postaci

pV_m = RT

a dla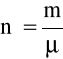
moli ( m - masa rozpatrywanego gazu;
- jest masą 1 mola gazu, czyli masą cząsteczkową wyrażoną w jednostkach masy)

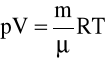
Zazwyczaj w takiej formie zapisu równanie opisujące zachowanie mocno rozrzedzonych gazów jest nazywane równaniem stanu gazu doskonałego.

Równanie to można zapisać także w innej postaci, wprowadzając stałą

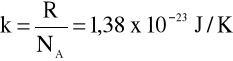
nazywaną stałą Boltzmanna.

Otrzymujemy

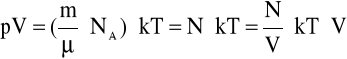
a stąd

p = n k T

gdzie: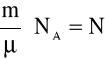
jest liczbą cząsteczek rozpatrywanego gazu o masie m,

zaś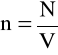
liczbą drobin na jednostkę objętości, czyli koncentracją gazu.

Prosty związek między T i pozostałymi parametrami gazu doskonałego pozwala przyjąć go jako substancję termometryczną i otrzymać termometr o idealnie liniowej skali temperatur.

Opis ciepła

Ciepło dostarczone do układu, lub przekazane od układu wiąże się ze zmianami temperatury. Ilość ciepła potrzebna do zmiany temperatury ciała o wartość jednostkową jest wielkością charakterystyczną dla danego ciała i nosi nazwę pojemności cieplnej tego ciała. Z tego określenia wynika wzór definicyjny pojemności cieplnej ciała

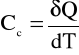
wyrażanej w jednostce J/K.

Uwzględniając definicję ciepła właściwego substancji c - ilość ciepła potrzebna do zmiany o jednostkę temperatury jednostki masy danej substancji - jeśli masa substancji wynosi m , to zachodzi oczywista relacja

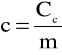
przy czym ciepło właściwe wyrażamy w jednostkach J/(kg K).

W termodynamice najczęściej stosowaną jednostką ilości materii jest 1 mol; w związku z tym definiuje się pojęcie ciepła molowego C jako ilości ciepła, potrzebną do zmiany temperatury o jednostkę dla 1 mola substancji.

Ponieważ masa 1 mola jest równa masie cząsteczkowej/atomowej
wyrażonej w jednostkach masy, wynika stąd prosty związek

Ciepło molowe jest wyrażane w jednostkach J/(mol K).

Ilość ciepła dostarczoną do układu n^' moli substancji obliczamy więc, stosując wzór

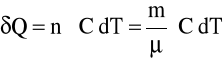
gdzie m - jest masą danej substancji.

- 5 -

1-ciepło i temperatura

---