Podstawy Metod Komputerowych w Obliczeniach Inżynierskich rok akademicki 2004/05 Obowiązujące zagadnienia.

1. Charakterystyka środowiska MATLAB.

2. Formaty wyświetlania liczb.

3. Metoda zapisu wyrażeń matematycznych.

• Operatory działań (dla macierzy lub skalarów):

• Operatory działań tablicowych:

• Operatory relacji:

• Operatory logiczne.

4. Znaki specjalne i ich znaczenie (np. ...%;, []).

5. Zmienne specjalne.

6. Charakterystyka plików skryptowych i funkcyjnych.

7. Instrukcje strukturalne

• Instrukcja iteracyjna for

• Instrukcja iteracyjna while

• Instrukcja warunkowa if

• Instrukcja warunkowa switch.

8. Metody definiowania macierzy.

9. Konstruowanie wektorów (macierzy) przy użyciu specjalnych funkcji wspomagających.

10. Operacje macierzowe

• Odwracanie macierzy

• „Dzielenie" macierzy

• Iloczyn skalamy

• Dzielenie tablicowe

• Transpozycja tablicowa.

11. Własności macierzy.

12. Wektory i wartości własne.

13. Efektywna budowa funkcji i skryptów.

14. Zapis i wczytanie danych z pliku.

15. Podstawowe funkcje dla łańcuchów tekstowych (char, strcat, strvcat, strcmp, strncmp, isletter, strrep, strfind, eval ... ).

16. Przekształcenie liczb i macierzy w łańcuch.

17. Wykresy 2D

• Funkcje zarządzające (figure, subplot, hold, uicontrol ...)

• Funkcje rysujące (plot, plotyy, polar, fill, bar, stem ...)

• Funkcje opisowe (xlabel ...)

18. Wykresy 3D

• Etapy rysowania wykresów trójwymiarowych

• Funkcje rysujące wykres 3 D

• Dodatkowe funkcje wykresów 3D (shading, view ...).

19. Rozwiązywanie równania różniczkowego zwyczajnego.

20. Obliczanie numerycznie całki.

21. Rozwiązywanie układu równań nieliniowych.

22. Znajdowanie miejsc zerowych funkcji.

23. Skrócona definicja funkcji (inline).

24. Co to jest Simulink, co zawiera ?

25. Etapy tworzenia modelu w Simulinku.

Odpowiedzi :

1. Charakterystyka środowiska MATLAB

• Praca w środowisku języka MATLAB polega na wydawaniu poleceń, które po zatwierdzeniu wykonywane są przez interpreter.

• Podstawowym typem danych jest macierz rzeczywista lub zespolona.

• Możliwość przeprowadzenia obliczeń symbolicznych (na wzorach).

• Większą liczbę instrukcji można zapisać w zbiorze tekstowym zwanym skryptem.

• Łatwa wizualizacja wyników w postaci dwu oraz trójwymiarowych wykresów.

Podstawowymi danymi wykorzystywanymi przez MATLAB-a są liczby rzeczywiste, a ściślej mówiąc macierze składające się z liczb rzeczywistych. Z owych liczb składają się także liczby zespolone

• Liczby rzeczywiste

pi = 3.14159265

• Liczby zespolone

Oprócz liczb rzeczywistych elementami macierzy mogą być liczby zespolone, które można podawać w jednej z poniższych postaci:

z = a+b*i

z = a+b*j

z = a+b*sprt(-1)

gdzie a, b oznaczają liczby rzeczywiste, natomiast i, j oraz sqrt(-1) oznacza jednostkę urojoną

z = 2.0000 + 3.00001*j

• Łańcuch tekstowy (jako wektor)

tekst = 'Ala mam kota'

2. Formaty wyświetlania liczb

• Format stałoprzecinkowy

format short pi = 3.1416

format long pi = 3.14159265358979

• Format zmiennoprzecinkowy

format short e pi = 3.1416e+000

format long e pi = 3.141592653589793e+000

• Automatyczny dobór reprezentacji

format short g

format long g

• Inne formaty

format rat pi = 355/113

format hex pi = 400921fb54442dl8

UWAGA ! Obliczenia są zawsze wykonywane w formacie podwójnej precyzji.

3. Metoda zapisu wyrażeń matematycznych Operatory działań (dla macierzy lub skalarów):

+ dodawanie

- odejmowanie

* mnożenie

/ dzielenie

^ potęgowanie

Operatory działań tablicowych:

.* mnożenie tablicowe

./ dzielenie tablicowe

.^ potęgowanie tablicowe

W języku MATLAB-a nie zdefiniowano oddzielnego typu logicznego. Zamiast niego wykorzystuje się macierze przyjmując, że:

• logiczna prawda odpowiada macierzy zawierającej wyłącznie elementy niezerowe,

• fałsz - macierzy pustej lub zawierającej co najmniej jedno zero.

Własność tę wykorzystuje się zasadniczo w wyrażeniach warunkowych, używanych w in­strukcji if i while.

Operatory relacji:

< mniejsze od

<= mniejsze lub równe

> większe od

>== większe lub równe

== równe

~= nierówne (różne)

Przykład. Jeśli:

A=[1 2 3];

B=[0 2 4];

to wartością wyrażenia A<B stanie się [0 0 l ], wyrażenie A< =5 ma wartość [0 l l],

natomiast A==B przyjmuje wartość [0 l 0].

Operatory porównania, zwane również relacyjnymi, badają czy między odpowiadającym sobie elementami macierzy będącymi ich operandami zachodzi dana relacja, tworząc macierz zawierającą l tam, gdzie relacja zachodziła i O tam, gdzie nie była spełniona.

Operatory logiczne:

& AND (koniunkcja)

| OR (alternatywa)

xor różnica symetryczna

~ negacja

Przykład. Niech:

A=[1 O 2];

B=[0 2 -2]

Wówczas wartości wyrażeń logicznych, których operandami będą macierze A i B będą na­stępujące:

A|B=[1 1 1] :

A & B =[0 0 1]

xor(A, B)=[1 1 0]

~A=[0 1 0]

Zapis w postaci matematycznej Zapis w postaci MATLABa

t = (1/(1+p*x))^k

4. Znaki specjalne

Znak	Nazwa	Znaczenie
.	Kropka	(a) Oddzielenie części całkowitej i dziesiętnej; (b) Operacje tablicowe
,	Przecinek	Separator elementów tablicy
;	Średnik	(a) Znacznik końca linii powodujący nie drukowanie jej wyniku w konsoli; (b) Znacznik końca wiersza w macierzy
:	Dwukropek	Separator przy tworzeniu wektora; Znacznik „wszystkich elementów''
( )	Nawias okrągły	(a) Separator wyrażeń matematycznych; (b) Ogranicznik opisu elementów macierzy
[ ]	Nawias kwadratowy	Symbol tworzący nową tablice lub macierz
{ }	Nawias klamrowy	Symbol tworzący nową tablice komórkową lub strukturę
%	Procent	Symbol komentarza
'	Apostrof	(a) Symbol transpozycji; (b) Ogranicznik łańcucha tekstowego
...	Trzykropek	Znacznik ciągłości kodu w następnej linii

5. Zmienne specjalne

Ans zmienna standardowa

Pi wartość liczby pi

NaN wynik nie liczbowy (Not a Number). Jest wynikiem matematycznie niezdefiniowanych operacji - np. 0/0, inf/inf

Inf wynik nieskończoność (Infinity)

- inf wynik w minus nieskończoności

Oba wyniki typu inf są rezultatem operacji która przekracza z góry lub z dołu zakres arytmetyki komputera - np. 10/0 lub sinh(1000)

6. Charakterystyka plików skryptowych i funkcyjnych.

Skrypty	Funkcje
Programy zawierające większą liczbę linii kodu. Nie posiadają argumentów wejść ani wyjść Operują na danych w przestrzeni roboczej. Wielokrotne wykonywanie programu. Ponowna edycja programu.	Uniwersalny element programu obliczeniowego. Wymaga deklaracji zmiennych wejściowych i wyjściowych. Zmienne lokalne nie są widziane na zewnątrz funkcji.

7. Instrukcje strukturalne

Instrukcja iteracyjna for	Instrukcja iteracyjna while
for zmienna = wyrażenie ... instrukcja ... end	while wyrażenie_warunkowe ... instrukcja ... end
Instrukcja warunkowa if	Instrukcja warunkowa switch
if wyrażenie_logiczne_1 ... instrukcja_1; ... elseif wyrażenie_logiczne_2 instrukcja_2; else wyrażenie_logiczne_3 instrukcja_3; end	switch wyrażenie_przełączające case wartość_wyrażenia_przełączającego_1 instrukcja_1; case wartość_wyrażenia_przełączającego_2 instrukcja_2; ... otherwise instrukcja; end

8. Metody definiowania macierzy

• przez wymienienie elementów;

W nawiasach kwadratowych podaje się elementy macierzy oddzielając wiersze średni­kiem. Wyrazy w wierszy mogą być oddzielone spacją i/lub przecinkiem, np.:

A=[2 2 2 1; 1 2 3 1];

Jeśli w wierszu edycyjnym nie możemy (lub nie chcemy) umieścić wszystkich elementów wiersza macierzy, to możemy go zakończyć trzema lub więcej kropkami. Wówczas wyrazy podawane w następnym wierszu edycyjnym stanowią kontynuację określanego wiersza ma­cierzy. Tak więc polecenie:

A=[1 2 3 4 ... . 5 6 7 8];

jest równoważne poleceniu:

A=[1 2 3 4 5 6 7 8];

Pominięcie trzech kropek oznaczałoby zdefiniowanie macierzy o dwóch wierszach, co

byłoby równoważne poleceniu:

A=[1 2 3 4; 5 6 7 8];

Sekwencja oznaczająca koniec wiersza jest więc traktowana tak jak średnik rozdzielający wiersze definiowanej macierzy.

• przez wygenerowanie elementów;

Wykorzystujemy wyrażenie o postaci ogólnej:

min:krok:max Generuje ono wektor wierszowy o następującej budowie:

[ min, min+krok, min+2*krok,..., max] Jeśli parametr krok zostanie pominięty wyrażenie przyjmuje postać:

min:max

i powoduje wygenerowanie wektora wierszowego, w którym wartości kolejnych elementów

wzrastają co jeden:

[min, min+1, min+2,..., max]

Przykład:

Jeśli chcemy utworzyć macierz A o wyrazach od l do 10 w pierwszym wierszu oraz od l do 20 (co 2) w drugim, to należy wydać polecenie:

A=[1:10; 1:2:20]

• przez zbudowanie z innych macierzy;

Macierz można wygodnie budować z innych macierzy (konstrukcję taką stosuje się dość często). Z tym sposobem zetknęliśmy się przy omawianiu poprzedniej metody - utworzyliś­my macierz składającą się z dwóch, odpowiednio wygenerowanych wektorów. Tym razem przyjrzyjmy się jak tworzyć macierze złożone z podmacierzy o różnych rozmiarach.

Zdefiniowano następujące macierze:

co w MATLAB-ie zapisuje się w postaci:

A=[1 4 1; 2 0 1];

B=[3 1; 4 1];

C=[1 2 2 0 1; 2 4 7 1 0];

Wyrażenie:

D=[A B; C];

definiuje macierz D złożoną z podmacierzy A, B i C w następujący sposób:

Daje to w efekcie następującą postać macierzy D:

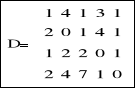
• przez mieszanie;

Przedstawione powyżej techniki można łączyć w zależności od potrzeb. Ilustruje to przy­kład, w którym za pomocą macierzy:

A=[1 2 3; 4 5 6];

definiujemy macierz:

D=[A,[1;2];1:4];

Jest nią macierz:

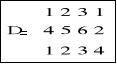
• przez użycie specjalnych funkcji.

9. Konstruowanie wektorów (macierzy) przy użyciu specjalnych funkcji wspomagających.

Funkcja.	Działanie.
rand ( )	generacja macierzy z elementami o wartościach losowych;
ones ( )	generacja macierzy wypełnionej jedynkami;
zeros ( )	generacja macierzy wypełnionej zerami;
Eye ( )	generacja macierzy jednostkowej;
diag( )	generacja macierzy diagonalnej z elementów podanych w wektorze, lub tworzenie wektora na podstawie diagonali macierzy.
linspace(x1,x2), linspace(x1,x2,N)	Generuje wektor wierszowy 100 liczb równomiernie rozmieszczonych między wartościami x1 i x2. Opcjonalny parametr N pozwala na określenie liczby generowanych wartości, np.: linspace(0, 20, 5) generuje wektor: [051015 20].
logspace(x1,x2), logspace(x1,x2,N)	Zwraca wektor wierszowy 50 liczb logarytmicznie, równo rozmieszczonych między wartościami 10^x1, a 10^x2. Parametr N pozwala samodzielnie określić liczbę generowa­nych wartości, np.: logspace(0, 3, 4) generuje wektor [l 10 100 1000].

Dodatkowe funkcje pomocnicze

disp(A)	Wysyła zawartość macierzy lub łańcucha (zob. p. 2.5) A do okna poleceń MATLABa. Nazwa zmiennej nie jest wypisywana na ekranie. Przypominamy, że wartość zmiennej będą­cej wartością wyrażenia będzie wysyłana na ekran, jeśli odpowiednie polecenie nie zostanie zakończone średnikiem.
[n, m] = size(A)	Zwraca liczbę wierszy m oraz kolumn n macierzy A.
n = size(A, 1)	Wyznacza liczbę wierszy macierzy A.
m = s/ze(A, 2)	Podaje liczbę kolumn macierzy A.
n = lenght (X)	Zwraca wymiar wektora X. Jeśli .Y jest macierzą zwracany jest dłuższy z jej wymiarów. Tak więc dla macierzy A zdefiniowanej w opisie funkcji size wywołanie: n=length(A) spowoduje nadanie zmiennej n wartości 4.

Macierze puste:

Przypisanie macierzy pustej [] elementowi macierzy lub pod macierzy powoduje

usunięcie tego fragmentu.

Uwaga: usuwany fragment macierzy może powodować zmianę jej wymiarów.

10. Operacje macierzowe

Dostęp do elementów macierzy:

Metody dostępu do elementów macierzy lub ogólniej: do podmacierzy przedsta­wione zostaną na przykładach. Zdefiniujmy zatem macierz A:

» A=[ 1 2 3 4 5 6; 0 9 8 7 6 5; 1 1 0 0 2 2]

A=

1 2 3 4 5 6

0 9 8 7 6 5

1 1 0 0 2 2

Odwołania do elementów

A(2, 4) odwołanie do czwartego elementu w drugim wierszu (wartość 7)

A(3, 3) odwołanie do trzeciego elementu w trzecim wierszu (wartość 0)

Odwołania do podmacierzy

A(1:2,1:2) odwołanie do podmacierzy rozpiętej między elementami (1,1) a (2, 2) czyli otrzymujemy macierz postaci: [1,2;0,9]

A(2,1:6) wiersza 2 macierzy A, równoważna konstrukcja A(2, :)

A([1 3],:) wiersze 1 i 3 macierzy A, tzn. macierz: [1 2 3 4 5 6; 1 1 0 0 2 2]

A(:,[1:3 5]) pobranie z macierzy A kolumn 1-3 oraz 5, tzn. macierz: [1 2 3 5; 0 9 8 6; 1 1 0 2]

A([1 3], 1:2:5) utworzenie macierzy z elementów leżących na przecięciu wierszy 1 i 3 z kolumnami 1, 3 i 5, tzn. macierz [1 3 5; 1 0 2]

Odwracanie macierzy

Zapis symboliczny	Zapis w składni MATLABa
A^-1	inv(a), A^-1

"Dzielenie" macierzy

Nazwa operacji	Składnia	Operacja równoważna
Dzielenie lewostronne	C\D	inv(C)*D
Dzielenie prawostronne	C/D	D*inv(C)

Algorytm użyty do wykonania dzielenia macierzy jest dobierany automatyczne zależy od struktury macierzy C, która może być macierzą trójkątną, symetryczną, kwadratową, prostokątną, pełną lub rzadką.

Iloczyn skalarny

Zapis symboliczny	Składnia języka MATLAB
x­­^Ty	x'*y, dot(x,y)

Dzielenie tablicowe

Nazwa operacji tablicowej	Składnia	Operacja równoważna
Dzielenie lewostronne	A.\B	B./A
Dzielenie prawostronne	A./B	B.\A

Transpozycja tablicowa

Zapis symboliczny	Składnia języka MATLAB
A°	A.'

Transpozycja tablicowa różni się tylko tym od transpozycji macierzowej, że w przypadku elementów zespolonych nie przekształca ich w elementy sprzężone.

11. Własności macierzy

• Rzędem macierzy X nazywa się liczbę jej niezależnych wierszy lub kolumn. Rzędem macierzy nazywamy stopień jej największego minora różnego od zera. Do obliczania rzędu macierzy służy komenda rank ( ),

• Śladem macierzy kwadratowej A nazywa się sumę elementów znajdujących się na głównej przekątnej. Do obliczania śladu macierzy służy komenda trace ( )

• Wyznacznik macierzy kwadratowej oblicza się komendą det.

W praktyce obliczenia polegają na przekształceniu macierzy do postaci trójkątnej, wtedy wyznacznikiem jest iloczyn elementów na przelotnej

12. Wektory i wartości własne.

Rozważmy przekształcenie n - elementowego wektora x

y = Ax Dla każdej macierzy A istnieją takie wektory v, które dają się wyrazić jako Av =λv

• Wektor v ≠ 0 nazywa się wektorem własnym macierzy A

• λ nazywa się wartością własna macierzy A

Wartości własne macierzy A są pierwiastkami równania det( A - λI )

Wartości własne macierzy A oblicza się komendą eig ( )

Charakterystyka M-plików funkcyjnych

• Samodzielnie tworzone procedury przez użytkownika w obrębie jednej funkcji przeznaczone do wielokrotnego wykorzystania;

• Nazwa M-pliku funkcyjnego, w którym jest zapisana funkcja musi być taka sama jak nazwa funkcji.

• Funkcje działają na zmiennych lokalnych i komunikują się z przestrzenia robocza poprzez parametry formalne wejścia i wyjścia;

• Wartości zmiennych zadeklarowanych jako globalne (polecenie global) są dostępne zarówno wewnątrz przestrzeni roboczej jak też wewnątrz funkcji.

• Funkcja po wywołaniu przechowywana jest w pamięci w postaci pseudokodu, usunięcie komendą clear.

function [lista argumentów wyjściowych]=...,

nazwa funkcji (lista argumentów wejściowych)

% komentarze

. . .

ciąg instrukcji

. . .

Uwaga!

Polecenie help nazwa_funkcj i powoduje wyświetlenie linii komentarza

umieszczonego pod nagłówkiem function.

Funkcja może być wywoływana z liczbą parametrów mniejszą od tej, która jest w definicji funkcji. Można to uzyskać przez stosowanie dwóch zmiennych:

nargin ( ) reprezentujących liczbę parametrów wejściowych;

nargout ( ) reprezentujących liczbę parametrów wyjściowych.

13. Efektywna budowa funkcji i skryptów

• WEKTORYZACJA kodu programu i algorytmów tzn. unikanie instrukcji iteracyjnych na rzecz operacji macierzowych oraz wykorzystania funkcji standardowych;

• unikanie zbędnego powiększania macierzy w trakcie obliczeń. Należy wcześniej deklarować macierze o odpowiednich rozmiarach

14. Zapis i wczytanie danych z pliku.

MATLAB umożliwia zapisanie w pliku wszystkich istniejących w danym mo­mencie zmiennych, przy czym możliwe jest wpływanie na postać takiego zbioru danych i określenie jego nazwy. Zapisane w pliku dane mogą zostać ponownie wczytane do pamięci. Zapis i odczyt danych jest realizowany poleceniami save i load omówionymi poniżej.

save

Polecenie to zapisuje zmienne w pliku dyskowym.

Warianty polecenia save

Polecenie	Opis
save	Zapisuje binarnie wszystkie zmienne w pliku matlub.mut.
save nazwa-pliku	Zapisuje binarnie wszystkie zmienne w pliku o podanej nazwie. Przyjmowane jest rozszerzenie .mat.
save nazwa-pliku nazwy-zmiennych	Zapisuje wybrane zmienne w pliku o podanej nazwie.
save nazwa-pliku nazwy-zmiennych -ascii	Zapisuje wybrane zmienne w pliku tekstowym o podanej nazwie używając 8-cyfrowego zapisu liczb. Zmienne tworzą tablice liczb umieszczone jedna pod drugą, nazwy zmiennych są pomijane.
save nazwa-pliku nazwy-zmiennych -ascii -double	Jw., ale liczby zapisane są z wykorzystaniem 16-cyfrowego zapisu liczb.
save nazwa-pliku nazwy-zmiennych -ascii -double -tabs	Jw., z tym, że liczby oddzielane są znakami tabu­latora, a nie spacjami

MATLAB zapisuje zmienne w postaci binarnej w sposób oszczędny, uwzględniając roz­miar i typ elementów macierzy. Postać tekstową wykorzystuje się zwykle do generowania (lanych do raportów oraz przenoszenia danych do innych programów.

load

Polecenie to wczytuje zmienne z pliku dyskowego.

Polecenie	Opis
load	Wczytuje zmienne zapisane w pliku matlab.mat.
load nazwa-pliku	Wczytuje zmienne zapisane w pliku o podanej nazwie. Przyjmowane jest rozszerzenie .mat.
load nazwa.rozszerzenie	Wczytane dane zostaną zapamiętane w macierzy o nazwie takiej, jak nazwa pliku.
load nazwa-pliku -ascii	Umożliwia wczytanie macierzy z pliku tekstowego, którego nazwa 'i nie zawiera rozszerzenia (bez opcji -ascii podanie samej nazwy pliku i spowodowałoby poszukiwanie pliku binarnego z rozszerzeniem i .mai). Wczytana zmienna jest zapamiętywana w macierzy o nazwie i takiej jak nazwa wczytywanego pliku. Dane muszą tworzyć tablicę prostokątną
load nazwa-pliku.rozszerzenie -mat	Umożliwia wczytanie binarnego pliku danych o podanej nazwie ' i rozszerzeniu różnym od .mat

15. Podstawowe funkcje dla łańcuchów tekstowych (char, strcat, strvcat, strcmp, strncmp, isletter, strrep, strfind, eval ... ).

S = `MATLAB'

S'

ANS=

M

A

T

L

A

B

Istnieje możliwość tworzenia macierzy, których wierszami są łańcuchy. W tym celu należy użyć funkcji str2mat np.

S = str2mat(`MATLAB', `i jego', `procedury')

S =

MATLAB

i jego

procedury

blanks(n) - tworzy łańcuch składający się z n znaków pustych (spacji)

łączenia łańcuchów dokonujemy w następujący sposób:

s = `MATLAB';

s1 = `i jego';

s2 = `procedury';

scompl = [s s1 s2]

scompl =

MATLAB i jego procedury

Kody ASCII poszczególnych znaków łańcucha można uzyskać funkcją abs, np.

>>abs(s)

ans =

77 65 84 76 65 66 32

isletter( ) sprawdza które z elementów łańcucha są literami tworząc macierz złożoną z zer i jedynek, gdzie jedynka wskazuje obecność litery, np.:

>>isletter(`abs-10-aqq')

ans =

1 1 1 0 0 0 0 1 1 1

strcmp () służy do porównywania łańcuchów, zwracając jeden gdy łańcuchy są identyczne, i 0 w przeciwnym razie

findstr () pozwala na znalezienie wszystkich wystąpień krótszego łańcucha w dłuższym, zwracając wektor pozycji, na których rozpoczynają się wystąpienia wspomnianego łańcucha. Ważna jest wielkość liter:

>>s = `MATLAB'

findstr(s, `A')

ans =

[2 5]

findstr(s, `a')

ans =

[]

int2str ( ) przekształca liczby całkowite w łańcuch

num2str ( ) przekształca dowolne liczy w łańcuch

eval(s1, s2) polecenie to wykonuje polecenia MATLABa znajdujące się w łąńcuchy s1, jeśli w trakcie ich wykonywania miał miejsce błąd, wykonywane są polecenia znajdujące się w łańcuchu s2.

a = input(`prompt') powyższe wywołanie wysyła na ekran podany łąńcuch zachęty I oczekuje na wprowadzenie informacji przez użytkownika. Informacją tą może być dowolne wyrażenie w języku MATLABa.

>>a=input(`Podaj polecenie:')

Podaj polecenie: sin(pi/2)

a =

1

16. Przekształcenie liczb i macierzy w łańcuch.

Patrz np. num2str () w punkcie 15

17. Wykresy 2D

• Funkcje zarządzające (figure, subplot, hold, uicontrol ...)

clg - czyści okno graficzne

close - zamyka okno

figure - otwiera okno graficzne

subplot(m,n,p) - pozwala rysować kilka wykresów obok siebie

m - liczba wykresów które mają się zmieścić w pionie

n - liczba wykresów które mają się zmieścić w poziomie

p - numer wykresu, który zostanie narysowany najbliższym wywołaniem funkcji plot, wykresy są numerowane w wierszach od lewej do prawej, a wiersze od góry do dołu

hold - zapobiega czyszczeniu okna graficznego przed rozpoczęciem rysowania

hold on

hold off

ishold - zwraca 1 gdy hold jest włączony w przeciwnym wypadku daje 0

axis - wymaga jednego parametru - cztero elementowego wektora, którego kolejne elementy:

[xmin xmax ymin ymax] określają zakresy skal na poszczególnych osiach układu współrzędnych.

axis([xmin xmax ymin ymax])

axis(`auto') - ustawia skalowanie automatyczne

axis(`manual') - wyłącza tryb automatycznego skalowania, „zamrażając„ aktualne wymiary układu

axis(`ij') - zmienia układ na „macierzowy”, układ tego typu ma początek w lewym górnym rogu okna, a pierwsza współrzędna określa położenie w pionie

axis(`xy') - przywraca układ kartezjański

axis(`equal') - zmienia wymiary prostokąta zawierającego wykres aby odcinki na obu osiach miały tą samą skalę (żeby koło było kołem a nie elipsą)

axis(`square') - powoduje, że obie osie mają tyle samo jednostek długości

axis(`normal') - usuwa restrykcję narzucane przez equal i square

axis(`image') - powoduję że układ dostosowuje się wymiarami do obrazu

axis(`off') - ukrywa osie wraz z ich nazwami

axis(`on') - przywraca wyświetlanie osi

uicontrol( ) - służy do tworzenia przycisków, przełączników, wyłączników, suwaków, pól edycyjnych, ramek i pól tekstowych.

id = uicontrol(nazwa_własności1,wartość1,nazwa_własności2,wartość2,...)

lub id = uicontrol(idf, nazwa_własności1,wartość1,nazwa_własności2,wartość2,...)

idf - identyfikator rysunku (okna), wewnątrz którego ma zostać utworzony element.

przykłąd - przykładowy program tworzy w lewym, dolnym rogu aktywnego okna przycisk z napisem „Czyść”, którego naciśnięcie powoduje oczyszczenie aktywnego układu współrzędnych.

Uicontrol(`style','pushbutton',...

`position,[10 10 100 20],…

`callback','cla')

uimenu ( ) - służy do tworzenia elementów menu głównego oraz elementów podmenu. Każde wywołanie funkcji powoduje utworzenie pojedynczego wiersza podmenu lub jednej opcji menu.

id = uimenu(nazwa_własności1,wartość1,nazwa_własności2,wartość2,...)

lub id = uimenu(idf, nazwa_własności1,wartość1,nazwa_własności2,wartość2,...)

menu ( ) - służy do łyskawicznego tworzenia samodzielnych menu. Wywołanie funkcji powoduje utworzenie nowego rysunku, na którym umieszczone są jeden pod drugim przyciski z nazwami kolejnych opcji. Naciśnięcie dowolnego z przycisków powoduje zamknięcie okna i zakońcxzenie działania funkcji.

menu(tytuł, opcja1, opcja2, opcja3, ...)

• Funkcje rysujące (plot, plotyy, polar, fill, bar, stem ...)

plot ( ) - rysuje wykresy nie koniecznie przedstawiające zależności funkcyjne, to znaczy pojedynczej wartości zmiennej x może odpowiadać więcej niż jedna wartość zmiennej y.

Działanie funkcji sprowadza się do łączenia odcinkami punktów o podanych współrzędnych, dzięki temu za jej pomocą można wykreślić praktycznie dowolną krzywą.

plot(y)

plot(x,y)

plot(x,y,s)

plot(x1,y1,x2,y2,…)

plot(x1,y1,s1,x2,y2,s2,…)

s - jedno-, dwu- lub trójznakowy łańcuch s zawierający kod koloru, oznaczenie typu linii lub jedno i drugie w takiej właśnie kolejności. Np.

`r:' - linia czerwona, kropkowana

`g- -` - linia zielona kreskowana

`wo' - białe kółeczka w punktach

Kod	Kolor
y	Żółty
M	Karmazynowy
C	Cyjan
R	Czerwony
G	Zielony
B	Niebieski
W	Biały
k	Czarny
Kod	Typ linii
.	Same podane punkty
O	Kółeczka w punktach
X	Iksy w punktach
+	Krzyżyki w punktach
*	Gwiazdki w punktach
-	Linia ciągła
- -	Linia kreskowana
:	Linia kropkowana
-.	Linia kreska - kropka

Poniższe funkcje loglog, semilogx, semilogy mają identyczne jak funkcja plot argumenty i wykonują podobne zadania.

loglog( ) - funkcja rysuje wykresy używając skal logarytmicznych

semilogx( ) - funkcja rysuje wykresy używając skali logarytmicznej na osiach odciętych

semilogy( ) - funkcja rysuje wykresy używając skali logarytmicznej na osiach rzędnych

fplot( ) - jest to funkcja służąca do szybkiego, wygodnego, i precyzyjnego rysowania wykresów zależności funkcyjnych.

fplot(f,granice)

fplot(f,granice,n)

fplot(f,granice,n,kąt)

fplot(f,granice,n,kąt,podprzedziały)

[x,y] = fplot(...)

f - łańcuch znaków stanowiący nazwę pliku zawierającego rysowaną funkcję)

granice - dwuelementowy wektor opisujący granice przedziału w jakim ma być narysowany wykres

Określenie precyzji z jaką ma być rysowany wykres umożliwiają dodatkowe opcjonalne argumenty\::

N - liczba określająca minimalną liczbę punktów, uwzględnianych przy sporządzaniu wykresu

polar ( ) - funkcja rysuje wykresy w układzie biegunowym

polar (t,r)

polar(t,r,s)

t - wektor zawierający wartości kątów dla poszczególnych punktów

r - wektor zawierający odległości poszczególnych punktów od początku układu

errorbar ( ) - rysuje wykres funkcji zaznaczając jednocześnie podane przez użytkownika odchylenia.

x,y współrzędne kolejnych punktów wykresu

e - wielkość odchyleń w każdym z punktów

bar( ) - funkcja rysuje wykres słupkowy.

bar(y) - rysuje kolejne słupki o wysokości y

bar(x,y) - rysuje kolejne słupki o wysokości y, elemnty wektora x muszą być uporządkowane rosnąco

bar(y,s) - rysuje kolejne słupki w wysokości y i wyglądzie linii s

bar(x,y,s)

[xx,yy] = bar(…)

stem( ) - funkcja rysuje wykres łodygowy, czyli słupki takie jak z bar zostały zastąpione odcinkami “wyrastającymi” z osi odciętych I zakończonymi kółeczkami.

stairs( ) - funkcja rysuje „schody” o stopniach na wysokości odpowiadającej wartościom elementów wektora y. Współrzędne odcięte krawędzi „stopni” określają elementy wektora x.

Stairs(y)

Stairs(x,y)

[xx,yy] = stairs(…)

hist( ) - funkcja robiąca histogram, czyli wykres obrazujązy liczbę elementów danego zbioru, którego wartości są zawarte w określonych przedziałach. System MATLAB oferuje dwie funkcje rysujące histogramy.

hist(y)

hist(y,n)

hist(y,x)

[n,x]=hist(...)

n - gdy n jest skalarem to n określa liczbę podprzedziałów. A jeśli n jest wektorem to jego elementy wyznaczają granicę przedziałów

rose( ) - funkcja rysuje histogram kołowy

rose(t)

rose(t,n)

rose(t,x)

[t,r] = rose(...)

t - wektor danych

n - skalar określający liczbę podprzedziałów

x - wektor określający położenie i wartości reprezentowane przez kolejne sektory

compass( ) - funkcja ta rysuje wykres, na którym elementy macierzy z są przedstawione w postaci strzałek o wspólnym początku i grotach w punktach opisanych przez współrzędne x=real(z), y=im(z).

compass(z)

compass(x,y)

compass(z,s)

compass(x,y,s)

Wywołanie z dwoma parametrami będącymi macierzami jest równoważne wywołaniu:

compass(x+i*y)

parametr s jest ciągiem znaków opisującym typ linii jaką mają być rysowane strzałki

feather( ) - funkcja ta rysuje wykres, na którym elementy macierzy z są przedstawione w postaci strzałek o początkach rozmieszczonych równomiernie na wspólnej, poziomej prostej.

feather(z)

feather(x,y)

feather(z,s)

feather(x,y,s)

Wywołanie z dwoma parametrami będącymi macierzami jest równoważne wywołaniu:

feather(x+i*y)

line( ) - funkcja ta rysuje linię składającą się z odcinków o końcach w punktach określonych przez elementy wektorów x i y. Jeżeli x i y są macierzami o takich samych wymiarach dla każdej kolumny macierzy rysowana jest jedna linia.

line(x,y)

fill( ) - funkcja ta wypełnia wielokąt o wierzchołkach w punktach wyznaczonych przez elementy wektorów x i y kolorem określonym przez argument c. Jeżeli jest to konieczne, wielokąt jest zamykany przez połączenie odcinkiem punktów: pierwszego i ostatniego.

fill(x,y,c)

fill(x1,y1,c1,x2,y2,c2,…)

patch( ) - funkcja, podobnie jak poprzednia, tworzy wypełnione wielokąty. Wektory x,y,i z określają współrzędne wierzchołków w 2D lub 3D, a parametr c jego kolor.

patch(x,y,c)

patch(x,y,z,c)

Kolor jest określany przez podanie indeksu koloru w powiązanej z aktualnym układem mapie kolorów lub za pomocą kodu. Podobnie jak w przypadku poprzedniej funkcji parametr c może być:

1. skalarem, wtedy płat będzie jednokolorowy

2. jednoznakowym ciągiem - płat będzie również jednoznakowy, oznaczenia kolorów są takie same jak w przypadku funkcji plot.

3. wektorem o takim samym wymiarze jak wektory x,y i z, wtedy elementy wektora okreśą kolory w odpowiednich wierzchołkach, kolory poszczególnych punktów wielokąta będą miały kolory pośrednie, płynnie zmieniające się w zależności od położenia punktu, kolor każdego punktu będzie wynikiem interpolacji dwuliniowej kolorów wirzchołków.

6. Funkcje opisowe (xlabel ...)

xlabel( ) - funkcja wypisuje łańcuch znaków tekst pod poziomą osią (osią x) aktywnego układu współrzędnych.

xlabel(tekst)

xlabel(tekst,nazwa_własności1,wartość1,nazwa_własności2,wartość2,...)

ylabel( ) - funkcja wypisuje łańcuch znaków tekst obok osi y aktywnego układu współrzędnych.

ylabel(tekst)

ylabel(tekst,nazwa_własności1,wartość1,nazwa_własności2,wartość2,...)

text( ) - funkcja wypisuje podany jako parametr tekst łańcuch znaków w aktywnym układzie współrzędnych, w miejscu określonym przez parametry x i y.

text(x,y,tekst)

grid( ) - polecenie grid on powoduje naniesienie na wykres pomocniczej siatki współrzędnych. Polecenie grid off chowa siatkę. Polecenie bez parametrów powoduje przełączenie wyświetlania siatki.

grid

grid on

grid off

18. Wykresy 3D

• Etapy rysowania wykresów trójwymiarowych

Aby poprawnie narysować wykres trójwymiarowy potrzebne są macierze X,Y i Z zawierające współrzędne punktów potrzebnych do wyrysowania wykresów. Owe współrzędne maja następującą postać: x=X(i,j), y=Y(i,j), z=Z(i,j). Można je zbudować ręcznie poprzez podanie współrzędnych ręcznie lub też skorzystać z funkcji meshgrid i meshdom. Owe funkcje służą do obliczeń współrzędnych punktów opisanych konkretnymi wzorami.

meshgrid( ) - funkcja ta tworzy macierze opisujące położenie węzłów prostokątnej siatki. Dziedziny zmiennych - położenie pionowych i poziomych „nici” siatki opisują parametry wejściowe - wektory x,y i z.

[X,Y]=meshgrid(x,y)

[X,Y]=meshgrid(x)

[X,Y,Z]=meshgrid(x,y,z)

Wiersze macierzy X są kopiami wektora x a kolumny macierzy Y są kopiami wektora y. Macierze wyjściowe X i Y mają length(y) wierszy i length(x) kolumn. Pojedynczy punkt siatki leżącej w jej k-tym wierszu i l-tej kolumnie ma współrzędne:

x_punktu=X(k,l)

y_punktu=Y(k,l)

Na przykład wartość funkcji:

f(x,y) = sin(x)sin(x)exp( -x² - y² )

obliczamy siatkę punktów (-pi + 0.2k, -pi + 0.2l ) za pomocą konstrukcji”

[X,Y]=meshgrid(-pi:0.2:pi, -pi:0.2:pi);

Z=sin(X).*sin(Y).*exp(-X.^2-Y.^2);

Otrzymane macierze X,Y i Z mają length(x) kolumn i length(y)*length(z) wierszy.

Na przykłąd aby utworzyć trójwymiarową siatkę punktów o jednostkowym „oczku” wypełniającą kostkę, należy wydać polecenie:

[X,Y,Z]=meshgrid(0:2,10:12,20:22)

otrzymane macierze mają postać:

X = 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2

Y = 10 10 10 11 11 11 12 12 12 10 10 10 11 11 11 12 12 12 10 10 10 11 11 11 12 12 12

Z = 20 21 22 20 21 22 20 21 22 20 21 22 20 21 22 20 21 22 20 21 22 20 21 22 20 21 22

meshdom( ) - funkcja ta jest funkcją meshgrid z poprzednich wersji programu.

• Funkcje rysujące wykres 3 D

mesh( ) - rysuje powierzchnię opisaną przez macierze x,y i z w postaci kolorowej siatki o oczkach wypełnionych kolorem tła. Elementy macierzy c określają kolory obwódek poszczególnych oczek

mesh(x,y,z,c)

mesh(x,y,z)

mesh(z,c)

mesh(z)

id=mesh(...)

meshc( ) - funkcja stanowi połączenie funkcji mesh i contour. Rysuje ona siatkę taką jak mesh, i umieszcza pod nią wykres poziomicowy. Owa funkcja ma identyczne parametry jak funkcja mesh.

meshc(x,y,z,c)

meshc(x,y,z)

meshc(z,c)

meshc(z)

id=meshc(...)

meshz( ) - funkcja ma działanie podobne do funkcji mesh, rysuje ona siatkę opisaną na macierzach x,y i z. Różnicz polega na tym, że w dół od krawędzi wykresu rysowane są „zasłony” - płaszczyzny odniesienia. Owa funkcja ma identyczne parametry jak funkcja mesh.

meshz(x,y,z,c)

meshz(x,y,z)

meshz(z,c)

meshz(z)

id=meshz(...)

surf( ) - funkcja rysuje różnokolorową powierzchnię opisaną macierzami x,y i z. Owa funkcja ma identyczne parametry jak funkcja mesh, z tym że c określa nie kolor „nici” siatki, lecz kolory jakimi wypełniane są oczka.

surf(x,y,z,c)

surf (x,y,z)

surf (z,c)

surf (z)

id= surf (...)

surfc( ) - funkcja stanowi połączenie funkcji surf i contour. Tak jak meshc.

surfc(x,y,z,c)

surfc(x,y,z)

surfc(z,c)

surfc(z)

id= surfc(...)

surfl( ) - funkcja rysuje powierzchnię z uwzględnieniem odbić światła.

surfl(x,y,z,s,k)

surfl(x,y,z,s)

surfl(x,y,z)

surfl(z,s)

surfl(z)

id= surfl(...)

s - wektor określający kierunek z którego pada światło

k - wektor o następujących kolejnych elementach:

1. natężenie światła rozproszonego w przestrzeni

2. współczynnik rozproszenia światła na powierzchni

3. współczynnik odbicia

4. współczynnik rozproszonego światła odbitego

waterfall( ) - rysuje wykres zbliżony wyglądem do tworzonego przez funkcję meshz z tym, że nie są rysowane linie odpowiadające kolumnom macierzy

waterfall(x,y,z,c)

waterfall(x,y,z)

waterfall(z,c)

waterfall(z)

id= waterfall(...)

• Dodatkowe funkcje wykresów 3D (shading, view ...).

zlabel( ) - funkcja wypisuje łańcuch znaków tekst obok osi z aktywnego układu współrzędnych.

zlabel(tekst)

zlabel(tekst,nazwa_własności1,wartość1,nazwa_własności2,wartość2,...)

text( ) - funkcja wypisuje podany jako parametr tekst łańcuch znaków w aktywnym układzie współrzędnych, w miejscu określonym przez parametry x,y i z.

text(x,y,z,tekst)

grid( ) - polecenie grid on powoduje naniesienie na wykres pomocniczej siatki współrzędnych. Polecenie grid off chowa siatkę. Polecenie bez parametrów powoduje przełączenie wyświetlania siatki.

grid

grid on

grid off

view( ) - funkcja view zmienia kierunek, z którego oglądany jest aktywny układ współrzędnych.

Parametry az i el określają odpowiednio azymut i elewację. Gdy funkcja view jest wywołana z pojedynczym parametrem liczbowym równym 2 powoduje to przyjęcie kierunku obserwacji używanego przy oglądaniu rysunków dwuwymiarowych. Gdy damy 3 to będzie przyjęcie kierunku obserwacji 3D.

view(az,el)

view([az,el])

view([x,y,z[)

view(2)

view(3)

viewmtx( ) - funkcja viewmtx zmienia kierunek, z którego oglądany jest aktywny układ na perspektywiczny.

viewmtx(az,el)

viewmtx(az,el,p)

viewmtx(az,el,p,x)

p -kąt widzenia unormowanego, widocznego prostopadłościanu i wpływa na stopień zniekształceń perspektywicznych.

x - wektor trójelementowy podający współrzędne obserwowanego punktu wewnątrz prostopadłościanu widzenia.

hidden( ) - funkcja usuwająca i przywracająca zasłonięte linie wykresu z ekranu

hidden on

hidden off

hidden

shading( ) - zmienia tryb kolorowania w wykresach aby uzyskać dany efekt cieniowania.

shading flat - zmniejsza ilość kolorów aby wykres wydawał się mieć mniejszą głębie

shading interp - interpoluje koloru co uwydatnia wszelkie nierówności na wykresie

shading facetd - to co flat z tym, że linie odgraniczające mają kolor czarny

s=shading

axis( ) - skalowanie przebiega tak jak dla wykresów 2D. Np.

axis([zmin xmax ymin ymax zmin zmax])

plot3( ) - funkcja analogiczna do plot dla 2D. Rysuje linie łamaną.

plot3(x,y,z)

plot3(x,y,z,s)

plot3(x1,y1,z1,s1,x2,y2,z2,s2,...)

contour( ) - funkcja rysuje wykres poziomicowy

contour(z)

contour(x,y,z)

contour(z,n)

contour(x,y,z,n)

contour(z,v)

contour(x,y,z,v)

contour(...,linia)

n - liczba poziomic jaka ma zostać narysowana, jeśli jej nie ma to wtedy jest tryb automatyczny.

v - wektor występujący zamiast zmiennej n, jego elementy określają jakim wysokością mają odpowiadać kolejne poziomice

linia - inaczej s ( patrz 2D w typach linii )

contour3( ) - funkcja rysuje wykres poziomicowy rozłożony na całej przestrzeni 3D na odpowiednich wysokościach.

contour3(z)

contour3(x,y,z)

contour3(z,n)

contour3(x,y,z,n)

19. Rozwiązywanie równania różniczkowego zwyczajnego.

Do rozwiązania równania różniczkowego należy skorzystać z funkcji ode23 lub ode45. Ka

[T,X] = ode23(`F(t,x)',t0,tk,x0,tol,tr)

[T,X] = ode45(`F(t,x)',t0,tk,x0,tol,tr)

Funkcje te rozwiązują zagadnienie początkowe dla układów równań zwyczajnych postaci:

dx/dt = F(t,x), x(t_o) = x_o ; x,x_o należa do Rⁿ

Każda z nich korzysta z pary metod Rungego - Kutty odpowiednio: rzędu 2 i 3 (ode23) oraz 4 i 5 (ode45). Kolejne parametry oznaczają:

1. łańcuch zawierający nazwę zdefiniowanej przez użytkownika funkcji zwracającj F(t, x)

2. t0, tk - granice przedziłu czasu, w którym poszukiwane jest rozwiązanie

3. x0 - określa warunek początkowy - wektor kolumnowy zawierający wartość rozwiązania układu w chwili początkowej

4. tol - opcjonaln parametr określający wymaganą dokładność, standartowo 10^-3

5. tr - opcjonalny parametr, który jeśli ma wartość różną od zera, to powoduje wypisanie kolejnych kroków działania metody na ekranie.

20. Obliczanie numerycznie całki.

Do obliczenia całek numerycznych stosujemy procedury quad lub quad8.

quad - kwadratura oparta o regułę Simpsona

quad8 - kwadratura ośmioprzedziałowa Newtona - Cotesa

Q = quad(f, a, b, tol)

Q = quad8(f, a, b, tol)

f - łąńcuch zawierający nazwę odpowiedniej funkcji, która musi być umieszczona w odpowiednim skrypcie

a,b - para liczb rzeczywistych określająca przedział całkowania

tol - wymagana tolerancja względna, jeśli jest brak to MATLAb przyjmuje 10^-3

np.

function [Y]=quadfun(X)

% funkcja

Y=sin(X.*X);

% koniec quadfun.m

Q=quad(`quadfun',0,pi) lub

Q=quad8(`quadfun',0,pi)

21. Rozwiązywanie układu równań nieliniowych.

fsolve

Solve a system of nonlinear equations




for x, where x is a vector and F(x) is a function that returns a vector value.

Syntax

x = fsolve(fun,x0)

x = fsolve(fun,x0,options)

[x,fval] = fsolve(...)

[x,fval,exitflag] = fsolve(...)

[x,fval,exitflag,output] = fsolve(...)

[x,fval,exitflag,output,jacobian] = fsolve(...)

Description

fsolve finds a root (zero) of a system of nonlinear equations.

x = fsolve(fun,x0) starts at x0 and tries to solve the equations described in fun.

x = fsolve(fun,x0,options) minimizes with the optimization options specified in the structure options. Use optimset to set these options.

[x,fval] = fsolve(fun,x0) returns the value of the objective function fun at the solution x.

[x,fval,exitflag] = fsolve(...) returns a value exitflag that describes the exit condition.

[x,fval,exitflag,output] = fsolve(...) returns a structure output that contains information about the optimization.

[x,fval,exitflag,output,jacobian] = fsolve(...) returns the Jacobian of fun at the solution x

Avoiding Global Variables via Anonymous and Nested Functions explains how to parameterize the objective function fun, if necessary.

Input Arguments

Function Arguments contains general descriptions of arguments passed in to fsolve. This section provides function-specific details for fun and options:

Fun

The nonlinear system of equations to solve. fun is a function that accepts a vector x and returns a vector F, the nonlinear equations evaluated at x. The function fun can be specified as a function handle for an M-file function x = fsolve(@myfun,x0) where myfun is a MATLAB function such as function F = myfun(x) F = ...            % Compute function values at x fun can also be a function handle for an anonymous function. x = fsolve(@(x)sin(x.*x),x0); If the Jacobian can also be computed and the Jacobian option is 'on', set by options = optimset('Jacobian','on') then the function fun must return, in a second output argument, the Jacobian value J, a matrix, at x. Note that by checking the value of nargout the function can avoid computing J when fun is called with only one output argument (in the case where the optimization algorithm only needs the value of F but not J). function [F,J] = myfun(x) F = ...          % objective function values at x if nargout > 1   % two output arguments    J = ...   % Jacobian of the function evaluated at x end If fun returns a vector (matrix) of m components and x has length n, where n is the length of x0, then the Jacobian J is an m-by-n matrix where J(i,j) is the partial derivative of F(i) with respect to x(j). (Note that the Jacobian J is the transpose of the gradient of F.)

options

Options provides the function-specific details for the options values.

Example 1. This example finds a zero of the system of two equations and two unknowns:




You want to solve the following system for x




starting at x0 = [-5 -5].

First, write an M-file that computes F, the values of the equations at x.

function F = myfun(x)

F = [2*x(1) - x(2) - exp(-x(1));

-x(1) + 2*x(2) - exp(-x(2))];

Next, call an optimization routine.

x0 = [-5; -5];           % Make a starting guess at the solution

options=optimset('Display','iter'); % Option to display output

[x,fval] = fsolve(@myfun,x0,options) % Call optimizer

x =

0.5671

0.5671

fval =

1.0e-006 *

-0.4059

-0.4059

Example 2. Find a matrix x that satisfies the equation




starting at the point x= [1,1; 1,1].

First, write an M-file that computes the equations to be solved.

function F = myfun(x)

F = x*x*x-[1,2;3,4];

Next, invoke an optimization routine.

x0 = ones(2,2); % Make a starting guess at the solution

options = optimset('Display','off'); % Turn off Display

[x,Fval,exitflag] = fsolve(@myfun,x0,options)

The solution is

x =

-0.1291 0.8602

1.2903 1.1612

Fval =

1.0e-009 *

-0.1619 0.0776

0.1161 -0.0469

exitflag =

1

and the residual is close to zero.

sum(sum(Fval.*Fval))

ans =

4.7915e-020

Notes

If the system of equations is linear, use the \ (the backslash operator; see help slash) for better speed and accuracy. For example, to find the solution to the following linear system of equations:




You can formulate and solve the problem as

A = [ 3 11 -2; 1 1 -2; 1 -1 1];

b = [ 7; 4; 19];

x = A\b

x =

13.2188

-2.3438

3.4375

22. Znajdowanie miejsc zerowych funkcji.

fzero( ) - funkcja służąca do wyznaczania miejsc zerowych

x = fzero(`F', x0, eps)

F - nazwa funkcji której mamy znaleźć miejsce zerowe. Musi być w postaci przyrównanej do zera np.

Z = sin(alfa) => Z - sin(alfa) = 0 => F = Z - sin(alfa)

x0 - początkowe przybliżenie wartości szukanego miejsca zerowego

eps - parametr opcjonalny, oznacza żadaną dokładność z jaką MATLAB ma wyznaczyć miejsce zerowe.

23. Skrócona definicja funkcji (inline).

inline

Construct an inline object

Syntax

g = inline(expr)

g = inline(expr,arg1,arg2,...)

g = inline(expr,n)

Description

inline(expr) constructs an inline function object from the MATLAB expression contained in the string expr. The input argument to the inline function is automatically determined by searching expr for an isolated lower case alphabetic character, other than i or j, that is not part of a word formed from several alphabetic characters. If no such character exists, x is used. If the character is not unique, the one closest to x is used. If two characters are found, the one later in the alphabet is chosen.

inline(expr,arg1,arg2, ...) constructs an inline function whose input arguments are specified by the strings arg1, arg2,.... Multicharacter symbol names may be used.

inline(expr,n) where n is a scalar, constructs an inline function whose input arguments are x, P1, P2, ... .

Remarks

Three commands related to inline allow you to examine an inline function object and determine how it was created.

char(fun) converts the inline function into a character array. This is identical to formula(fun).

argnames(fun) returns the names of the input arguments of the inline object fun as a cell array of strings.

formula(fun) returns the formula for the inline object fun.

A fourth command vectorize(fun) inserts a . before any ^, * or /' in the formula for fun. The result is a vectorized version of the inline function.

Examples

Example 1. This example creates a simple inline function to square a number.

g = inline('t^2')

g =

Inline function:

g(t) = t^2

You can convert the result to a string using the char function.

char(g)

ans =

t^2

Example 2. This example creates an inline function to represent the formula
. The resulting inline function can be evaluated with the argnames and formula functions.

f = inline('3*sin(2*x.^2)')

f =

Inline function:

f(x) = 3*sin(2*x.^2)

argnames(f)

ans =

'x'

formula(f)

ans =

3*sin(2*x.^2)ans =

Example 3. This call to inline defines the function f to be dependent on two variables, alpha and x:

f = inline('sin(alpha*x)')

f =

Inline function:

f(alpha,x) = sin(alpha*x)

If inline does not return the desired function variables or if the function variables are in the wrong order, you can specify the desired variables explicitly with the inline argument list.

g = inline('sin(alpha*x)','x','alpha')

g =

Inline function:

g(x,alpha) = sin(alpha*x)

24. Co to jest Simulink, co zawiera ?

Simulink jest to nakładka na MATLABa służąca do symulowania różnych zjawisk fizycznych jak i przekształceń matematycznych. Praca w simulinku polega na zbudowaniu symulowanego obiektu lub zjawiska z pojedyńczych klocków zwanych blokami. Każdy blok można opisać i każdy spełnia jakąś funcję matematyczną bądź jest odzwierciedleniem rzeczywistego obiektu np. jakiegoś przełącznika bądź urządzena do pomiarów. W Simulinku można np. stworzyć układ sterowania złożony ze źródeł sygnału, obiektów dynamicznych i przyrządów pomiarowych, a następnie, po dokonaniu obliczeń, zaprezentować wyniki uzyskane w MATLABie na wykresach Bodego.

25. Etapy tworzenia modelu w Simulinku.

1. Uruchamiamy MATLABa

2. Uruchamiamy nakładkę Simulink

3. Stwarzamy nowy projekt

4. wybieramy odpowiednie moduły z konkretnych bibliotek

5. opisujemy moduły zależnościami matematyczno - fizycznymi

6. łączymy moduły w obiekt

7. Uruchamiamy symulację

8. Zapisujemy wyniki

9. kończymy pracę z MATLABem i Simulinkiem

---