AKADEMIA TECHNICZNO-HUMANISTYCZNA

W BIELSKU-BIAŁEJ

WYDZIAŁ NAUK O MATERIAŁACH I ŚRODOWISKU

ROK I, SEM.II.

SPRAWOZDANIE Z LABORATORIUM

FIZYKI.

Temat: WYZNACZANIE PRZYŚPIESZENIA ZIEMSKIEGO ZA POMOCĄ WAHADŁA REWERSYJNEGO.

Wykonali:

Marek Tittor

Barbara Fojcik

Anna Dziergas

Cel ćwiczenia:

Celem ćwiczenia jest zapoznanie się z podstawowymi zagadnieniami związanymi z analizą pola grawitacyjnego Ziemi.

Część teoretyczna:

Przyspieszeniem ziemskim nazywamy przyspieszenie swobodnego spadku ciał pod wpływem ich ciężaru Q. Zgodnie z II zasadą dynamiki:

gdzie: g - przyspieszenie ziemskie,

m - masa ciała.

Przyspieszenie ziemskie zmienia się w niewielkim zakresie w różnych punktach powierzchni Ziemi ze względu na zmienność ciężaru. Ciężar jest wypadkową skierowaną do środka Ziemi siły grawitacji oraz odśrodkowej siły bezwładności spowodowanej ruchem obrotowym Ziemi wokół jej osi:

Wartość siły bezwładności oraz jej kierunek względem kierunku siły grawitacji są zależne od szerokości geograficznej. Z tego powodu ciężar ciała jest wielkością zmienną zależną od miejsca na Ziemi, w którym ciało się znajduje.

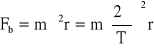
gdzie: ω - prędkość kątowa ruchu obrotowego Ziemi,

T - okres obiegu Ziemi wokół jej osi,

r - promień okręgu po którym porusza się ciało.

Wahadło rewersyjne (odwracalne)- bryła sztywna, która zawieszona kolejno na dwóch osiach równoległych leżących po przeciwnych stronach jej środka ciężkości w nierównych od niego odległościach, ma taki sam okres drgań.

Przebieg ćwiczenia:

Zawieszamy wahadło na jednym z jego ostrzy-01, przesuwamy masę M na środek pręta. Wykonujemy serię m=10 pomiarów czasu t dziesięciu drgań (n=10) bez zmiany położenia masy M. Następnie wyniki umieszczamy w Tab. 1 i na ich podstawie obliczamy wartość średnią t i średni błąd kwadratowy St pojedynczego pomiaru skorygowany przez odpowiedni współczynnik Studenta-Fishera: S_t =tα,mS't.

Tab. 1.

t1 [s]	t2 [s]	t3 [s]	t4 [s]	t5 [s]	t6 [s]	t7 [s]	t8 [s]	t9 [s]	t10 [s]
18	18,22	18,38	18,09	18,22	18,59	18,35	18,25	18,46	18,65

t_śr= 18.32 s

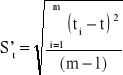
=0,055 S_t=t_α,mS'_t =0,13

t	S't	tα,m	St
18,32	0,055	2,3	0,13

Przesuwamy masę M do ostrza swobodnego O2 i wykonujemy serię pojedynczych pomiarów czasów t' dziesięciu drgań przesuwając masę M w kierunku osi wahadła co 5 cm. Następnie obracamy wahadło i zawieszając je na drugiej osi postępujemy jak wyżej- mierzymy czas t'', a wyniki zapisujemy w tabeli 2.

Tab.2

	Oś I	Oś II
kn [cm]	t [s]	t [s]
5	19,81	19,81
10	19,66	18,46
15	19,04	18
20	19	18,06
25	18,69	17,47
30	18,65	17,40
35	18,34	17,56
40	18,40	17,69
45	18,63	17,60
50	18,68	17,50
55	18,56	17,91
60	18,34	18,16
65	18,44	18,12
70	18,97	18,50
75	18,91	18,82
80	19,18	19,29
85	19,44	19,56
90	19,78	19,81
95	19,40	20,34

Na podstawie wykresu określamy współrzędne t'0 i t''0 punktów przecięcia krzywych t'=(kn) i t''=(kn).

t'=18,06 t''=19

Obliczamy średni czas 10 drgań t0 = (t'0 + t''0)/2

t0 = (18,06 + 19)/2 = 18,53

szacujemy błąd ∆t₀ = [S_t² +(∆t'₀)²]^1/2

gdzie ∆t'₀ = |t'₀ - t''₀| /2

∆t'₀ = 0,47

∆t₀ = 0,49

Obliczamy okres drgań wahadła T₀.

T₀ = t/n = 1,83

Obliczamy przyspieszenie ziemskie g i błąd bezwzględny ∆g ze wzorów:

g_ob = (4π²n²l)/(t₀²) g_ob = (400π²l)/(400) = 9,86

Wyniki umieszczamy w tabeli 3.

∆g = g_ob {|(∆l/l)| + 2|(∆t₀/t₀)| ∆g = 9,86 (|0,005m/1m| + 2|0,49/18,53|) = 0,57

t'0 = 18,06 [s]	t''0 = 19 [s]	t0 = 18,53 [s]	∆t'0 = 0,47 [s]	∆t0 = 0,49 [s]
T0 = 1,83 [s]	l = 1 [m]	∆l = 0,005 [m]	g = 9,86 [m/s]	∆g = 0,57 [m/s]

---