RÓWNANIE FOURIERA.
Dotyczy analizy wymiany ciepła w stanie nieustalonym przez przegrodę płaskąrys.
Równanie przewodnictwa:
q=−λ⋅∂T/∂x. (strumień ciepła jest proporcjonalny do temperatury).
Q1=fq1Δτ czyli ΔQ=fΔτ(q2-q1) , ale
Q=Vρcpτ=fΔxρcpτ. Zatem prawo zachowania energii cieplnej:
∂q/∂x = −cp⋅ρ⋅∂T/∂τ.
(λ - wsp. przewodzenia ciepła charakt. dla danego materiału [W/(mK)]; cp - ciepło właściwe materiału, z którego wykonana jest przegroda [J/kgK]; ρ - gęstość materiału [kg/m3]; q - gęstość strumienia cieplnego [W/m2]). Różniczkując równanie przewodnictwa po x i wstawiając do pr. zach. energii cieplnej otrzymujemy równanie różniczkowe Fouriera: λ⋅∂2T/∂x2 = cp⋅ρ⋅∂T/∂τ (inna postać: a⋅∂2T/∂x2 = ∂T/∂τ, gdzie a = λ/cp⋅ρ. Żeby to równanie rozwiązać, potrzebne są warunki brzegowe. Do rozwiązania stosuje się metodę różnic skończonych.
WSPÓŁCZYNNIKI a I b
(Z ROZWIĄZANIA RÓWNANIA FOURIERA)
Rozwiązujemy równanie Fouriera (dot. nieustalonej wymiany ciepła przez przegrodę płaską) o postaci: λ⋅∂2T/∂x2 = = cp⋅ρ⋅∂T/∂τ metodą różnic skończonych dla następujących założeń
Otrzymujemy:
λ⋅∂T/∂xi ≈ λi ⋅ {Ti - T(i - 1)}/Δxi
λ⋅∂T/∂xi + 1 ≈ λi + 1⋅ {Ti +1 - Ti}/Δxi +11
λ⋅∂2T/∂x2 = ∂/∂x⋅(λ⋅∂T/∂x) i+1 ≈
≈ {λ i +1⋅(Ti + 1 - Ti )/Δxi + 1 - λi ⋅ (Ti -
- Ti - 1)/Δxi }/Δxi + 1
cp⋅ρ⋅∂T/∂τi ≈cp i ⋅ρi ⋅(Ti - Ti)/Δτ; gdzie: λi - współczynnik przewodzenia ciepła i-tej elementarnej warstwy,
cp i - ciepło właściwe materiału, z którego wykonana jest i-ta elementarna warstwa,
Δxi - grubość i-tej elementarnej warstwy,
ρi - gęstość materiału i-tej elementarnej warstwy,
Ti - temperatura w i-tej płaszczyźnie podziału przegrody,
Ti - temperatura w i-tej płaszczyźnie podziału przegrody, w chwili wcześniejszej.
Po przekształceniach otrzymujemy równanie różnicowe dla i-tej płaszczyzny podziału przegrody (i = 2,3,..,n-2; ponieważ dla przegród skrajnych są dane warunki brzegowe):
hi ⋅ Ti - 1 + ri ⋅ Ti + 1 - ki ⋅ Ti + 1 = Ti, gdzie: hi = {Δτ/Δxi ⋅Δxi +1 }⋅λi/ /
cp i ⋅ ρi ;
ki = {Δτ/(Δxi +1 )2}⋅λi + 1 / cp i ⋅ ρi;
ri = 1 + hi (1-ai-1)+ ki.; a0=0
hi , ki , ri - bezwymiarowe liczby Fouriera.
Dla pierwszej płaszczyzny podziału równanie ma następującą postać:
r1 ⋅ T1 - k1 ⋅ T2 = T1 + h1 ⋅ T0. St¹d:
T1 = T2k1/r1 + (T1 + h1 ⋅ T0)/r1.
Wprowadzając oznaczenia: a1 = k1/r1 ; b1 = (T1 + h1 ⋅ T0)/r1 otrzymujemy:
T1 = a1 ⋅ T2 + b1 i podstawiamy do równania dla drugiej płaszczyzny podziału. Po przekształceniach otrzymujemy dalej:
T2 = T3 ⋅ k2/r2 + (T2 +
+h2 ⋅ b1)/ r2. Przyjmując takie same oznaczenia: a2 = k2/r2;
b2 = (T2+ h2 ⋅ b1)/ r2 , a więc:
T2 = a2 ⋅ T3 + b2. Uogólniając dla pozostałych płaszczyzn: Ti = ai ⋅ Ti + 1 + + bi , przy czym: a0 =0 , b0 = T0 , ai= ki/ri ; bi = (Ti + hi ⋅ bi - 1)/ri (ai oraz bi dla i = 1 , 2 , . . . , n - 1 )
gdzie ri = 1 + (1 - ai -1)hi + ki
RÓWNANIE BILANSU CIEPŁA. WARUNKI POCZĄTKOWE I BRZEGOWE.
Q1= f q1 Δτ [ J ]
gdzie:
f - powierzchnia [ m.2]
q1 - strumień [W/m2]
Δτ - przedział czasowy [s]
Δ Q = f Δτ (q2 - q1) - przegroda musi wchłonąć tę warstwę ciepła
Δ Qc = V ρ cw T [ J ]
gdzie V = f Δx
Δ Q + Δ Qc = 0
0=f Δτ (q2 - q1) + f Δx ρ cw T / f
Równanie to oparte jest na prawie zachowania energii.
,
,
warunek brzegowy I rodzaju:
określa zmienność w czasie temp. powierzchni przegrody.
warunek brzegowy II rodzaju:
przebieg zmienności strumienia ciepła w czasie po obu stronach przegrody.
warunek brzegowy III rodzaju:
określa równania które ujmują procesy przejmowania ciepła na powierzchniach.
KOMFORT CIEPLNY
Jest to zespół warunków w których człowiek czuje się dobrze albo źle. Czynniki mające wpływ na samopoczucie człowieka: temp. wszystkich przegród wewnętrznych, promieniowanie otoczenia (powietrze nie bierze udziału w procesie promieniowania, jeżeli nie zawiera za dużo), wilgotność powietrza (utrata ciepła przez parowanie skóry),ruch powietrza (prędkość przepływu powietrza w pomieszczeniu), stan samego człowieka (czy stoi, czy leży, czy pracuje). WENTYLACJA NATURALNA jest to samoistny ruch powietrza, które dostaje się przez nieszczelności a wydostaje się przez kratki wentylacyjne. Wady - duże straty ciepła, wysokie nakłady inwestycyjne, brak możliwości regulacji parametrami (powietrze, wilgotność, temperatura), brak możliwości odzyskiwania ciepła. WENTYLACJA MECHANICZNA jest niezależna od warunków zewnętrznych i odbywa się za pomocą mechanicznego wprowadzania powietrza w ruch (wentylatory). Głównymi zadaniami są: dostarczanie niezbędnej ilości świeżego powietrza, usuwanie starego, dostosowanie do potrzeb wentylacji poszczególnych pomieszczeń. OCIEPLANIE stosuje się po to aby nie było przemarzania ścianek, co by doprowadziło do pęknięć.
ODWZOROWANIE STRUKTURY BUDYNKU NA GRAF, WIERZCHOŁEK, ŁUK GRAFU, MACIERZ INCYDENCJI.
Każdą strukturę budynku, a dokładnie przestrzeń każdego pomieszczenia można odwzorować przy pomocy punktów, które tworzą graf.
Graf jest więc formalnym zapisem struktury budynku. Posiada on wierzchołki, które są odwzorowaniem przestrzeni wewnętrznych pomieszczeń, płaszczyzny przekroju gruntu na pewnej głębokości oraz przestrzeni otaczającej budynek. Wierzchołki grafu połączone są między sobą łukami grafu. Łuki te odwzorowują drogi przepływu ciepła między poszczególnymi wierzchołkami.
Graf przepływu, którego wierzchołkom i łukom przypisano zbiory stałych i zmiennych wartości oraz określonych na tych zbiorach funkcje nazywa się siecią przepływu ciepła. Natomiast graf przenikania, którego wierzchołkom i łukom przypisano zmienne i stałe wartości fizyczne oraz opisane na tych zbiorach funkcje nazywa się siecią przenikania ciepła. Funkcje opisane na ww zbiorach określają gęstość strumienia ciepła np. qi=ki⋅fi⋅Δti . Do stałych i zmiennych wartości należą natomiast: pole powierzchni wymiany ciepła, współczynniki przenikania ciepła, strumień ciepła.
Numeryczną reprezentacją grafu jest macierz incydencji. W macierzy takiej wszystkie wiersze przypisane są wierzchołkom grafu, a wszystkie kolumny - łukom.
A=[ai,j], gdzie i=1,2,...,m −liczba wierzchołków
j=1,2,...,n − liczba łuków.
W każdej komórce tej macierzy powinna być wpisana liczba:
1 − jeżeli i-ty wierzchołek jest
początkiem j-tego łuku,
0 − jeżeli i-ty łuk nie jest incydentny z
i-tym wierzchołkiem,
-1 − jeżeli i-ty wierzchołek jest końcem
j-tego łuku.
Np. :

ZADANIE OBLICZANIA TEMP. W POMIESZCZ. NIEOGRZEWANYCH, WZÓR NA WEKTORY TEMPERATURY.
Przystępując do obliczenia temperatury w pomieszczeniach nieogrzewanych należy najpierw narysować graf przenikania ciepła, a następnie odpowiadającą mu macierz incydencji A. Potem trzeba podzielić ją na dwie części: tę której odpowiadają temperatury niewiadome − An oraz wiadome − Ad.
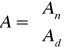

Wiemy, że An⋅q=q0 , gdzie q - wektor strumienia, którego elementami są wartości strumienia; q0 - wektor, którego elementami są zyski strumienia: q0=qq+qd−qinf (qd - q dodatkowe, qinf -q infiltracji).

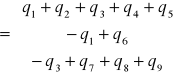
Ale również: q=F⋅K⋅Δt, gdzie F - macierz diagonalna z wartościami pola powierzchni; K - macierz diagonalna, której wszystkie wartości są równe 0 oprócz przekątnych, bo ich wartości są równe współczynnikom przenikania ciepła.
Ponadto Δt=AT⋅t, gdzie:
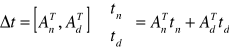
Czyli:
Rozwiązując dalej otrzymujemy:
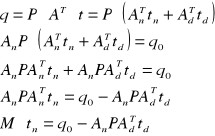
M- macierz.
Ostatecznie można wyprowadzić wzór na wektory temperatury:
![]()
gdzie:
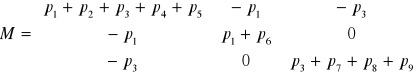
jest to macierz symetryczna.
ANALIZA PROCESU WYMIANY CIEPŁA I WILGOCI W MOSTKACH
Jest to wc i ww w narożnikach i stropie. Przyjmujemy ruch ustalony. Zajmujemy się przypadkiem dwuwymiarowym (wymiana ciepła w dwóch kierunkach), kroimy mostek w miejscu, w którym może wykroplić się para
Przegrody dzielimy na warstwy elementarne (obliczanie liczb Fouriera).
W środkach geometrycznych elementów po podzieleniu i na ich krawędziach graniczących z otoczeniem znajdują się wierzchołki grafów.
Na krawędziach a i b warunek brzegowy II rodzaju.
Łuki - droga przepływu ciepła między wierzchołkami grafów.
Po wewnętrznej i zewnętrznej stronie przegrody po jednym wierzchołku grafu ( temperatury). Między tymi wierzchołkami a wierzchołkami na krawędziach zewnętrznych łuki. Wewnątrz przegrody tylko łuki poziome i pionowe (wg rys) między najbliższymi wierzchołkami.
Mogą się zdarzyć takie przypadki podziału przegrody
gdzie P - współczynnik przewodności
WYMIANA WILGOCI ( PARA WODNA) W BUDYNKACH
Zgodnie z prawem Daltona w mieszaninie gazów ciśnienie całkowite jest równe sumie ciśnień cząstkowych.
Ciśnienie cząstkowe pary w stanie nasycenia zależy od temperatury.
Wilgotność względna
CIEPŁO |
--- prawo Fouriera |
Współczynnik przewodzenia ciepła k
|
Natężenie strumienia ciepła q=k(ti-te)[W/m2] |
Równanie Fouriera
|
PARA |
- współczynnik przepuszczalności pary P - przewodność pary (strumień masy pary przepływający przez przegrodę |
|
Natężenie strumienia pary w=(pi-pe)/rp[g/m2h] pi, pe - ciśnienia cząstkowe pary wodnej
psi, pse - ciśnienie nasycenia w danej temp. - wilgotność względna |
- współczynnik parochłonności materiału |
ETODA RÓŻNIC SKOŃCZONYCH , ELEMENTARNE.
Opór przewodzenia ciepła przegrody złożonej można przedstawić wzorem:![]()
Gdzie:RII-opór przewodzenia ciepła przy podziale przegrody złożonej płaszczyznami adiabatycznymi
R1-opór przewodzenia ciepła przy podziale przegrody przegrodami izotermicznymi
m.-współczynnik zależny od rodzaju przegrody. Metodę różnic skończonych stosujemy dla określenia oporów cieplnych i współczynników przenikania ciepła k dla dowolnych przegród niejednorodnych.
Równanie różniczkowe ustalonego przewodzenia ciepła w jednorodnym obszarze dwuwymiarowym zapisane w różnicach skończonych:
![]()
Uwzględniając postać różnic skończonych temperatury(rys)
Przy pominięciu wyrazów wyższych rzędów 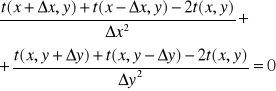
W celu wyprowadzenia podobnej postaci dla pola niejednorodnego mnożymy równanie Laplace'a przez (-λ) 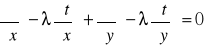
![]()
W praktyce na obszar, w którym chcemy określić pole temperatury narzuca się siatkę prostokątną przy czym węzły siatki numeruje się kolejno. Przy siatce kwadratowej dla punktu o określonym numerze temperaturę podaje wzór: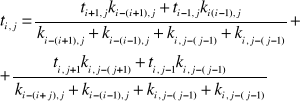
Jeżeli między dwoma węzłami na całej szerokości umownego pasa znajduje się jeden materiał , to współczynnik przenikania ciepła między tymi węzłami jest równy:
K=λ/Δ
APROKSYMACJA RÓWNANIA RÓŻNICZKOWEGO RÓWNANIEM RÓŻNICOWYM.
Przegrodę dzielimy na powierzchnie elementarne (rys.)
![]()
Po aproksymacji otrzymujemy kolejno równania:
dla płaszczyzny pierwszej Δx1
r1T1-k1T2=h1T0+T1
-dla warstwy środkowej Δx, Δxi+1
-hiTi-1+riTi - kiTi+1=Ti
-Dla warstwy ostatniej Δxn
-hnTn-2+rn-1Tn-1+knTn=Tn-1
r1 |
-k1 |
|
|
|
|
-h2 |
r2 |
-k2 |
|
|
|
|
-k3 |
r3 |
-k3 |
|
|
|
|
-k4 |
r4 |
-k4 |
|
|
|
|
-k5 |
r5 |
-k5 |
|
|
|
|
-k6 |
r6 |
=
T1+h1T0 |
T2 |
T3 |
|
|
T6+h6T6 |
Macierz rozwiązujemy za pomocą metody Cranka - Nicolsona dla macierzy trój diagonalnej
MACIERZ CYKLI.
Luki są odwzorowaniem dróg przepływu powietrza. Cykl - koniec jednego łuku jest początkiem następnego
Półcykl - ciąg zamkniętych łuków, w którym nie ma jednakowej orientacji przepływu
Macierz cykli której elementy określają przynależność do cykli
B=[bij] i=1,2...m
J=1,2...n
bij=:
1 - jeżeli tyj łuk należy do i-tego półcyklu i kierunek łuku jest przyjęty za dodatni
-1 - jeśli j-ty należy do i - tego i kierunek jego jest przeciwny
0 - jeżeli j - ty łuk nie należy do i-tego cyklu
Macierz sporządza się na podstawie poprawnie wykreślonego grafu
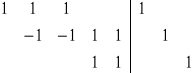
BR
B=[BRBD]
BR-rozgałęzione
BD-domykające
BD=I - macierz jednostkowa
B=[BRI]
INFILTRACJA POWIETRZA:
Infiltracja-powolne przenikanie powietrza przez wszystkie nieszczelności budynku. Związana jest ona z działalnością wiatru, który wytwarza pewne ciśnienie oraz ciśnieniem grawitacyjnym(wyporu), które wywołane jest różnicą temperatury.
-wart. char. dla okien okr. doświadczalnie
-róż. ciś. po obu str. okna
-ciś. wiatru w środku okna
-ciś. grawitacyjne w środku okna
-współ. aerodynamiczny
PROMIENIOWANIE
Dla ułatwiania określania problemu promieniowania zostały przyjęte uproszczenia: wszystkie powierzchnie przegród są płaszczyznami, przewodzenie ciepła odbywa się tylko w kierunku prostopadłym do powierzchni przegrody, przegrody są szare tzn. zdolność promieniowania jest równa zdolności pochłaniania, każdy element przegrody ma jednakową temp. i zdolność promieniowania, wszystkie powierzchnie emitują i odbijają promieniowanie zgodnie z prawem Lamberta, powietrze w pomieszczeniu nie emituje nie pochłania i nie rozprasza promieniowania cieplnego, temperatura powietrza w przekrojach pomieszczeń jest stała, a zmienia się liniowo wg. założonego gradientu w przekrojach pionowych.
PRAWA: PLANCKA- Na podst. teorii kwantów w sposób teoretyczny określił rozkład widmowego strumienia emisji dla ciała doskonale czarnego w zależności od długości fali i temp. pow. bezwzgl. ciała doskonale czarnego
WIENA- Ujmuje zależność międzyi wartością temp. bezwzgl. ciał doskonale czarnych :
KIRCHOFFA- W tych samych warunkach temperaturowych ciał iloraz emisji do absorpcyjności dowolnych ciał szarych jest stały i równy strumieniowi emisji ciała doskonale czarnego i zależy od temp. - ciała które mało emitują to mało pochłaniają. BOLTZMANA -Aby określić cały strumień emisji dla pow. ciała doskonale czarnego przy określonej temp. bezwzgl. tej pow. należy określić pole pod krzywą temp. w zakresie od 0 do niesk.
-całkowity strumień emisji dla ciała dosk. czarnego.- stała prom. dla ciała doskonale czarnego =
W praktyce stosuje się jednak wzór:
Cc - techniczna stała promieniowania ciała dosk. czarnego = 5,37. Prawo to ważne jest również dla ciał szarych ale wtedy Cc = C = od 0 do 5,37.
LAMBERTA - Jeżeli intensywność emisji jest jednakowa we wszystkich kierunkach to gęstość strumienia emisji pow. płaskiej maleje proporcjonalnie do cos. odchylenia od kierunku prostopadłego do pow. emitującej promieniowanie
-gęstość strumienia emisji w kierunku odchylonym ood prostopadłego do pow. płaskiej
FUNKCJA ODPOWIEDZI:
Funkcja odpowiedzi określa odpowiedź przegrody na skokową lub impulsową zmianę temperatury zewnętrznej lub wewnętrznej.
Własności funkcji odpowiedzi:
związek między a :
2.
3.
Jeżeli:
Odpowiedź strat ciepła budynku jest sumą odpowiedzi dla poszczególnych przegród pomnożonych przez pola powierzchni tych przegród.
HAŁAS.
Hałas to dźwięk lub inne zaburzenie akustyczne nieprzyjemne lub niepożądane. O zagrożeniu hałasem mówimy wtedy, gdy istnieje jego odbiorca - osoba narażona na jego szkodliwe oddziaływanie.
Dźwięk - drganie akustyczne - zjawisko falowe wywołane ruchem cząsteczek ośrodka sprężystego wokół ich położenia równowagi, dźwięk prosty (ton) to drganie akustyczne sinusoidalne.
Dźwięk słyszalny - drganie akustyczne zdolne do wywołania wrażenia słuchowego (16Hz - 165kHz); wszystkie <16Hz to infradźwięki, a > 16kHz to ultradźwięki.
Ciśnienie akustyczne chwilowe , p - różnica między ciśnieniem istniejącym w danym punkcie ośrodka w danej chwili, a ciśnieniem statycznym(np.: atmosferycznym)
Ciśnienie akustyczne odniesienia - w ośrodkach gazowych przyjęte umownie jako równe p0=20 μPa
Moc akustyczna źródła dźwięku, W - całkowita energia akustyczna wypromieniowana przez źródło dźwięku w określonym paśmie częstotliwości w pewnym przedziale czasu, podzielona przez ten przedział. Moc akustyczna odniesienia jest równa W0=1pW/m
Natężenie dźwięku, l - strumień energii akustycznej o określonym kierunku i zwrocie, przenikający przez powierzchnię prostopadłą do tego kierunku, podzielony przez pole tej powierzchni. Natężenie akustyczne odniesienia jest równe I0=1pW/m2
Pochłanianie dźwięku - właściwość materiałów i obiektów, polegająca na zdolności do zmiany energii akustycznej na cieplną podczas rozchodzenia się dźwięku w ośrodku lub przy padaniu dźwięku na granicę między dwoma ośrodkami
Współczynnik pochłaniania dźwięku, α - część energii akustycznej padającej na daną powierzchnię i nie odbitej od tej powierzchni (przy danej częstotliwości i w określonych warunkach)
Czas pogłosu T - prędkość, z jaką maleje poziom ciśnienia akustycznego dla danej częstotliwości, a dokładniej czas upływający od chwili, gdy do punktu obserwacji w przestrzeni ograniczonej powierzchniami odbijającymi przestaje dochodzić pierwsza fala bezpośrednia po przerwaniu emisji działającego dostatecznie długo źródła dźwięku, do chwili, w której poziom ciśnienia akustycznego będzie mniejszy o 60dB (czyli ciśnienie akustyczne zmniejszy się milion razy)
Poziom - logarytm stosunku wartości danej do wartości odniesienia tej samej wielkości przy określonej podstawie logarytmu, wartości odniesienia i rodzaju poziomu. Jednostką poziomu jest bel (częściej stosowany decybel = 0.1 bel'a). Jest to jednostka poziomu wielkości proporcjonalnej do mocy, gdy podstawą10, natomiast jednostka poziomu wielkości określającej pole (np.: ciśnienia akustycznego) gdy podstawą jest pierwiastek 10.
Podstawowe wielkości:
a) poziom ciśnienia akustycznego:
b) poziom natężenia dźwięku:
c) poziom mocy akustycznej:
gdzie:
S - pole powierzchni pomiarowej prostopadłej do kierunku rozprzestrzeniania się fali
S0 - poziom powierzchni odniesienia
Poziom mocy akustycznej źródła hałasu wyznaczany jest na podstawie wyników badań laboratoryjnych lub terenowych. Polskie normy, a także normy międzynarodowe określają kilka metod wyznaczania poziomu mocy akustycznej. Metody te mają różną dokładność i stosowane są zależnie od potrzeb i możliwości technicznych. Ogólnie można je podzielić na dwie grupy:
badania w polu swobodnym w komorze bezechowej lub w przestrzeni otwartej
badania w warunkach pola rozproszonego w komorze pogłosowej lub w pomieszczeniu w którym zainstalowane jest badane urządzenie
d) równoważny poziom ciśnienia akustycznego:
w przypadku gdy poziom ciśnienia akustycznego ma w odcinkach czasu wartość stałą wzór przyjmuje postać:
2
p1
p2
p3
p4
p5
p0
p5
p4
p3
p0
p2
p1
u6
u5
u2
u7
u9
u4
u8
u1
u3
w3
w1
w2
w5
w4
w5
w2
w3
w1
w4
u2, u7, u4
u5, u8
u6
u1
u3
u9
u6
u5
u2
u7
u9
u4
u8
u1
u3
w3
w1
w2
w5
w4
w5
w2
w3
w1
w4
u2, u7, u4
u5, u8
u6
u1
u3
u9
An⋅q=q0
b
a
słup betonowy o innej własności
droga łączenia wierzchołków
λ1
λ2
T1
T2
Tp
Δx1
Δx2
y
T(x+Δx,y+Δy)
T(x,y+Δy)
T(x-Δx,y-Δy)
T(x+Δx,y)
T(x,y)
T(x-Δx,y)
T(x-Δx,y-Δy)
T(x+Δx,y-Δy)
T(x,y-Δy)
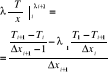
B0
Wyszukiwarka
Podobne podstrony:
fizyka budowli 2, budowictwo pcz (h.fresh06), II rok (sem III i sem IV), sem III, fizyka bud, ściągi
fizyka budowli 5, budowictwo pcz (h.fresh06), II rok (sem III i sem IV), sem III, fizyka bud, ściągi
wilgoc, Wapw, fizyka budowli prezentacje
Zal-lab-BP-zaoczne, politechnika lubelska, budownictwo, 3 rok, semestr 5, fizyka budowli, wykład
Fizyka proj 3, Budownictwo UTP, semestr 3, Fizyka Budowli
Dlugopis(1), Budownictwo PK, Fizyka budowli
test-B, politechnika lubelska, budownictwo, 3 rok, semestr 5, fizyka budowli, wykład
Izolacje i sciany zadanie, Fizyka Budowli - WSTiP, Budownictwo ogólne, Budownictwo Ogólne
Fizyka budowli wykład I Żelaz
Fizyka budowli do kola
Fizyka budowli część XVI Propozycja zmian wymagań ochrony cieplnej budynków
ściąga z fizyki, dc, GPF, Fizyka lab, Ściągi, sciąga z fizyki
SCIAGI PRAWO BUDOWLANE - wersja do wydruku, 1. Semestr V, Prawo Budowlane, Ściągi
test-d(1), politechnika lubelska, budownictwo, 3 rok, semestr 5, fizyka budowli, wykład
komun piwnica do druku, Fizyka Budowli - WSTiP
więcej podobnych podstron