Układy równań liniowych

W przeprowadzonym doświadczeniu przeprowadziliśmy analizę rozwiązywalności układu równań liniowych metodą iteracyjną Jakobiego. Metody te opierają się na stworzeniu takiego ciągu wektorów rozwiązań, aby był on zbieżny do rozwiązania prawdziwego. W każdej iteracji jest więc dokonywane przekształcenie wektora X w taki sposób, że w k+1 kroku procedury, i-ta składowa rozwiązania wyraża się zależnością:

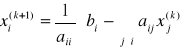
Procedura kończy się, gdy zostanie spełnione kryterium stopu.

W naszym zadaniu posłużyliśmy programem napisanym w Matlabie. Poniżej umieściliśmy fragment kodu źródłowego.

while sqrt(norma)>e&licznik<100000

licznik=licznik+1;

for i=1:n

suma=0;

for j=1:n

if j~=i

suma=suma+a(i,j)*x(j);

end

end

y(i)=(b(i)-suma)/a(i,i);

end

norma=0;

for i=1:n

norma=norma+(x(i)-y(i))^2;

end

if licznik<=100

war(licznik)=sqrt(norma);

end

x=y;

end

Po wprowadzeniu przez użytkownika macierzy A i B układu równań program ten losuje pierwsze przybliżenie wektora rozwiązań jako n liczb z przedziału [-100;100]. Kolejne przybliżenia obliczane są zgodnie z powyższym wzorem. Procedura kończy się w momencie gdy spełniony zostanie warunek stopu, czyli odległość miedzy kolejnymi przybliżeniami będzie mniejsza od wprowadzonej przez użytkownika wartości e.

Sprawdziliśmy działanie algorytmu dla kilku przykładów i doszliśmy do wniosku, że metoda ta ma pewne ograniczenia. Okazało się, że dla wielu przykładów macierzy A i B zmienne obliczane przez program w kolejnych iteracjach nie były zbieżne ale „uciekały” do nieskończoności. Poniżej przedstawiliśmy wybrane przez nas przykłady. Na wykresach przedstawiono zależność pomiędzy wartością przybliżeń rozwiązań a liczbą wykonanych przekształceń wektora X. x(1) jest pierwszym przybliżeniem rozwiązania wylosowanym przez program a licznik jest ilością iteracji wykonanych przez program.

A=[1 2;3 4]

B=[5;6]

e=0.000001

x(1)=[36;-60]

A=[1 2 3; 4 5 6;7 8 9]

B=[1;3;6]

e=0.000001

x=[-30;25;64]

A=[3 1;2 4]

B=[5;6]

e=0.000001

licznik=21

x(1)=[35;31]

A=[1.3 1;1 1]

B=[2;15]

e=0.000001

licznik=138

x(1)=[60;-13]

A=[7 1 2;3 8 4;5 6 9]

B=[25;0;-50]

e=0.000000001

licznik=130

x(1)=[-29;66;17]

A=[1 1;1 1]

B=[2;3]

e=0.000001

x(1)=[-74;13]

Jak widać na powyższych wykresach zbieżność ciągu przybliżeń zależy od macierzy A. W literaturze znaleźliśmy warunek zbieżności tego ciągu. Mówi on o tym, że ciąg kolejnych przybliżeń jest zbieżny wtedy i tylko wtedy gdy wartości na przekątnej głównej macierzy A są silnie dominujące nad pozostałymi elementami tej macierzy. Powyższe przykłady potwierdzają prawdziwość tego twierdzenia. Ponadto widzimy, że przybliżenia rozwiązania tym szybciej zbiegają do prawdziwego rozwiązania im bardziej dominujące są wartości na przekątnej.

---