AGH , Wydz. EAIiE Katedra Automatyki Napędu i Urządzeń Przemysłowych			Imię , nazwisko : JAROSŁAW GANDZEL
TEORIA STEROWANIA I TECHNIKA REGULACJI			Semestr : letni .
Rok akademicki : 1998 / 99	Rok studiów : II		Grupa : II
Kierunek : ELEKTROTECHNIKA			środa , godz . 10^00 .
Temat ćwiczenia : Komputer w układzie automatycznej regulacji.			Nr ćwiczenia : 5 .
Data wykonania ćwiczenia : 28.04.1999.		Data zaliczenia sprawozdania :

Mając do czynienia z nieznanym obiektem (czarną skrzynką) wykonujemy pomiary sygnałów wejściowych i wyjściowych a następnie możemy użyć programu komputerowego Matlab do analizy tego obiektu.

Analizę obiektu można podzielić na następujące etapy:

-identyfikację,

-modelowanie,

-regulację,

-napisanie programu na mikroprocesor.

Proces identyfikacji obiektu , którego wynikami liczbowymi dysponujemy i mamy opisujące go równania różniczkowe, polega na dobraniu odpowiednich współczynników tak aby odzwierciedlały wyniki liczbowe (przez porównanie odpowiedzi).

Jako model obiektu może nam posłużyć układ oparty o wzmacniacz operacyjny. Realizuje on funkcje różnych podstawowych członów układów automatycznej regulacji.

I tak w naszym przypadku posłuży on nam za element inercyjny:

Równania różniczkowe opisujące wzmacniacz możemy zastąpić równaniami transmitancyjnymi, oraz przedstawić cały wzmacniacz w postaci transmitancji zastępczej:

Przyjmując za
= k , a za R_SC_S=T dostajemy ostatecznie:

Czyli transmitancję członu inercyjnego.

Jeżeli połączymy dwa człony inercyjne jak na poniższym rysunku to otrzymamy układ drugiego rzędu reprezentujący szeroką gamę obiektów, procesów opisywanych równaniem różniczkowym drugiego rzędu.

Schemat rzeczywisty członu dwuinercyjnego:

Schemat blokowy w postaci transmitancyjnej:

Proces identyfikacji (dyskretny):

Proces identyfikacji obiektu , którego wynikami liczbowymi dysponujemy i mamy opisujące go równania różniczkowe, polega na dobraniu odpowiednich współczynników tak aby odzwierciedlały wyniki liczbowe (przez porównanie odpowiedzi).

Mamy nieznany układ:

Następnie dobieramy formułę matematyczną.

y(n)=f[y(n-1)........y(n-k₁),u(n-1).........u(n-k₂­)]

y(n)=a₁y(n-2)+a₂y(n-1)+a₃u(n-1)

1.Obiekt pierwszego rzędu:

Równanie różniczkowe dla obiektu inercyjnego pierwszego rzędu ma postać:

Natomiast równanie różnicowe:

Wykorzystując metodę najmniejszych kwadratów szukamy takich wartości współczynników „a” i „b” aby suma kwadratów różnic była jak najmniejsza. Jest to dla nas funkcja celu.

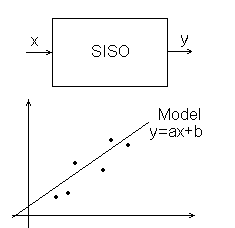
Korzystając z modelu jednoinercyjnego dokonujemy analogicznych przekształceń:

Wykorzystując metodę najmniejszych kwadratów szukamy takich wartości współczynników „a” i „b” aby suma kwadratów różnic była jak najmniejsza. Jest to dla nas funkcja celu.

A teraz rozpatrzmy metodę najmniejszych kwadratów dla układów wielowymiarowych:

y(n)= a₁x₁+ a₂x₂+ a₃x₃

Ogólna postać macierzowa równań dla układu wielowejściowego wygląda następująco:

Możemy także napisać funkcję błędu dla takiego układu:

Wykorzystując poniższe przekształcenia możemy doprowadzić do wyznaczenia wektora współczynników [a]:

(A+B)^T=A^T+B^T

(AB)^T=B^TA^T

A^TB=B^TA

(λA)^T=λA^T

Q=(Y +Xa)^T ⋅(Y-Xa)=(Y^T-a^TX^T) ⋅ (Y-Xa)=Y^TY - Y^TXa - a^TX^TY + a^TX^TXa

Q=Y^TY - 2a^TX^TY + a^TX^TXa

X^TXa = X^Ty / ⋅X^TX

a=(X^TX)^-1 X^T Y det(X^TX)≠0

1

4

---