Marcin Wolański Wrocław 1999-04-22

III rok fizyki komputerowej czwartek godz. 14³⁰

Prowadzący dr S. Dacko

TEMAT:

BADANIE ROZKŁADU ENERGETYCZNEGO TERMOELEKTRONÓW.

I. ZAGADNIENIA TEORETYCZNE.

1. Model pasmowy ciała stałego.

Pasmowy model ciała stałego jest to teoria opierająca wyjaśnienie własności ciał stałych (metali półprzewodników i dielektryków) na założeniu, że energie elektronów wchodzących w ich skład nie są dowolne, lecz należą do ściśle określonych zakresów, zwanych dozwolonymi pasmami energetycznymi. Pasma te są rozdzielone wzbronionymi pasmami energetycznymi, tzn. zakresami wartości energii, których nie może mieć żaden elektron znajdujący się w ciele stałym..

Przyjęcie schematu quasi - swobodnego elektronu w periodycznym polu potencjału umożliwia wniknięcie w istotę mechanizmu przewodnictwa elektrycznego w ciałach stałych, a w szczególności w metalach. Przy tworzeniu się cząstek czy kryształów, obraz poziomów energetycznych pojedynczego atomu zmienia się wskutek wzajemnego oddziaływania atomów na siebie. Rozważymy dla przykładu układ N atomów wodoru. Jeżeli atomy te znajdują się względem siebie w bardzo dużych odległościach, to w takim układzie występuje poziomy energetyczne elektronów takie jak w pojedynczym atomie wodoru. W miarę jak następuje zbliżanie się atomów do siebie, poziomy energetyczne ulegają rozszczepieniu. W takim przypadku w myśl zasady Pauliego, która mówi, że dwa elektrony nie mogą być opisane przez ten sam zespół liczb kwantowych, każdy z poziomów musi się rozpaść na N stanów. W przedstawionym schemacie występuje rozszczepienie stanów pierwotnych, z których każdy rozpada się na N nowych stanów. Przechodząc do ciał krystalicznych można przyjąć, że ze względu na bardzo dużą liczbę atomów w krysztale następuje rozszczepienie atomów na tak dużą liczbę poziomów, iż powstają pasma o praktycznie ciągłych zakresach energii. Elektron pochodzący z danego poziomu energetycznego będzie mógł będzie mógł przyjmować jedną z wielu zbliżonych do siebie wartości energii tworzących pasmo energetyczne. Elektrony zaczną przenikać do sąsiednich atomów w wyniku tunelowania przez wystarczająco cienkie obszary, w których energia potencjalna elektronu jest wyższa niż jego energia całkowita. Dzięki tunelowaniu elektrony zyskują swobodę poruszania się po całym krysztale, stanowiąc rodzaj gazu, tzw. gaz elektronowy.

Elektrony rozmieszczone są w pasmach energetycznych (rys. 1) oddzielonych przedziałami energii, w których nie ma dozwolonych stanów elektronowych; takie wzbronione przedziały nazywamy przerwami energetycznymi.

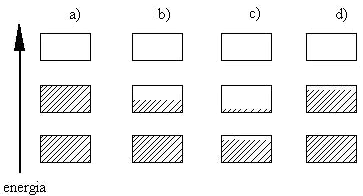
Jeżeli kryształ zawiera taką liczbę elektronów, że dozwolone pasma energetyczne są albo całkowicie wypełnione, albo puste, to wówczas elektrony nie mogą poruszać się w polu elektrycznym i kryształ zachowuje się jak izolator. Jeżeli jedno lub więcej pasm jest częściowo zapełnione, to kryształ zachowuje się jak metal. Jeżeli wszystkie pasma są całkowicie zapełnione z wyjątkiem jednego lub dwóch

Rys. 1. Model obsadzania elektronami dozwolonych pasm energetycznych w izolatorze, metalu, i dwóch półprzewodnikach. Pionowe rozmiary prostokątów przedstawiają dozwolone obszary energii, pola zacieniowane oznaczają obszary wypełnione elektronami.

pasm , które są tylko nieznacznie zapełnione lup prawie puste, to wówczas kryształ jest półprzewodnikiem.

Jedną z zasadniczych własności metali jest to, że elektrony odłączają się w nich łatwo od atomów, które w ten sposób przekształcają się w jony dodatnie. Jony te są rozmieszczone wewnątrz metalu w postaci regularnej sieci przestrzennej, charakterystycznej dla krystalicznej budowy metalu. Siły, wywierane przez jony sieci krystalicznej na elektrony odłączone od atomów metalu, znoszą się wzajemnie, wskutek czego elektrony te mogą się swobodnie poruszać wewnątrz metalu. Znajdują się one w ciągłym bezładnym ruch podobnie jak cząstki gazu w zamkniętym naczyniu. Ze względu na to podobieństwo mówi się często o gazie elektronowym w metalu. Jakkolwiek elektrony wchodzące w skład gazu elektronowego mogą się swobodnie poruszać pomiędzy jonami sieci krystalicznej metalu, to jednak w normalnych warunkach nie mogą go opuścić. Na powierzchni metalu siły wywierane na elektrony przez jony sieci krystalicznej nie znoszą się. Lecz mają wypadkową siłę skierowaną do wnętrza metalu. Ażeby wydostać się z metalu, elektron musi pokonać działanie tych sił, czyli musi wykonać pewną pracę, zwaną pracą wyjścia. Działanie sił wiążących elektron z metalem można interpretować jako istnienie tuż przy powierzchni metalu pewnej bariery potencjału, która przeciwdziała wyjściu elektronów z metalu. Przebieg energii potencjalnej dla elektronu znajdującego się w pobliżu powierzchni metalu przedstawiono na rysunku 2.

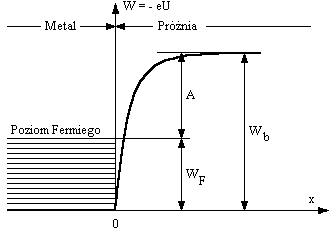
Rys. 2. Przebieg energii potencjalnej elektronu na granicy metal - próżnia

Wb - wysokość bariery potencjału;

WF - energia Fermiego;

A - praca wyjścia

W lewej części rysunku (wnętrze metalu)zaznaczono w sposób schematyczny poziomy energetyczne elektronów przewodnictwa w metalu w temperaturze zera bezwzględnego. Jest to najniższy stan energetyczny gazu elektronowego. W tej temperaturze obsadzane są przez elektrony wszystkie najniższe poziomy energetyczne, aż do pewnego poziomu granicznego odpowiadającego tzw. energii Fermiego W_F. Jeżeli elektronom w metalu dostarczymy dodatkowej energii to część elektronów zajmie wyższe poziomy energetyczne. Niektóre z nich będą miały energię wyższą od W_b i będą mogły wydostać się na zewnątrz metalu. Przy wyjściu elektronu z metalu zostaje wykonana praca wyjścia, której wartość jest równa różnicy energii W_b i energii Fermiego. Praca ta wyraża się wzorem

przy czym potencjał ϕ nosi nazwę potencjału wyjścia. Wartość pracy wyjścia zależy od rodzaju materiału.

2. Gaz elektronowy w metalach - statystyki i prawa nim rządzące.

Do opisu gazu elektronowego w metalach stosujemy uproszczony model metalu, w którym zaniedbujemy periodyczne pole elektryczne jonów sieci krystalicznej i traktujemy elektrony jako swobodne (z tym, że ich masa może różnić się od rzeczywistej masy elektronu). Elektrony obsadzają stany o możliwie najniższych energiach, lecz ze względu na zakaz Pauliego zajmowany są stany o stopniowo coraz wyższych energiach, do energii Fermiego włącznie, gdy natomiast stany o energiach wyższych od energii Fermiego są wolne. Cząstki dla których stosowana jest zasada Pauliego nazywamy fermionami (spin połówkowy), a statystykę je opisującą statystyką Fermiego. Można ją przedstawić na wykresie, na którym na osi poziomej odkłada się wartość energii elektronów, a na osi pionowej - liczbę elektronów mających daną wartość energii (rys. 2).

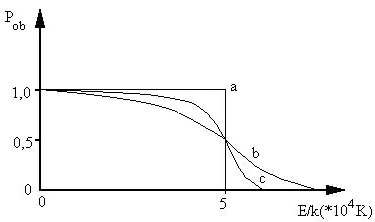
Rys. 2. Funkcja rozkładu Fermiego w różnych temperaturach. P_ob - prawdopodobieństwo obsadzenia,

a - 0 K, b - 1×10⁴ K, c - 5000 K.

3. Rodzaje emisji elektronów, wzór Richardsona - Dushmana.

Elektron aby wydostać się z metalu, musi mięć pewną, dość znaczną energię. W normalnych temperaturach energie kinetyczne elektronów w metalu są niewielkie i tylko najszybsze elektrony mogą pokonać siły wiążące je z metalem. Ilość takich elektronów jest jednakże tak znikomo mała, że emisji w tych warunkach możemy praktycznie nie brać pod uwagę. W celu wywołania emisji musimy dostarczyć elektronom dodatkowej energii. W zależności od sposobu doprowadzania tej energii rozróżniamy następujące zasadnicze rodzaje emisji: termoelektrodową, fotoelektrodową i wtórną.

Emisja termoelektronowa występuje wskutek nagrzania danego ciała (np. metalu) do odpowiednio wysokiej temperatury. Przy podwyższonych temperaturach metalu część elektronów znajduje się na wyższych poziomach energetycznych. Niektóre z elektronów mogą wydostać się poza barierę potencjału. Im wyższa jest temperatura metalu, tym większymi energiami dysponują elektrony przewodnictwa i tym większa ich ilość może wydostać się z metalu. Prąd emisyjny wzrasta więc wraz ze wzrostem temperatury. Zależność gęstości prądu emisyjnego od temperatury ciała emitującego ujmuje wzór Richardsona (zwany często w literaturze wzorem Richardsona - Dushmana):

w którym a i b są to stałe zależne od rodzaju ciała emitującego, T zaś oznacza jego temperaturę bezwzględną. Według teorii emisji elektronów stała a jest dla czystych metali niezależna od rodzaju metalu, czyli jest stałą uniwersalną. W rzeczywistości dla większości metali o doskonale oczyszczonych i odgazowanych powierzchniach stała a ma wartość 60A/cm²K²; natomiast dla powierzchni niejednorodnych (np. dla katod aktywowanych) odbiega ona bardzo znacznie od tej wartości i zawiera się w granicach od 0,01 do ok. 15 A/cm²K². Zależy ona przy tym w dużym stopniu od zastosowanych procesów technologicznych. Stała b jest związana z potencjałem wyjścia elektronów zależnością
przy czym k oznacza stałą Boltzmana = 1,381×10^-23 J/K. Wzór Richardsona można również zapisać w postaci

gdzie T to temperatura bezwzględna, A praca wyjścia. Ten rodzaj emisji jest wykorzystywany we wszystkich lampach z katodą żarzoną. Elektrony emitowane z metalu mają energię początkową wynikającą z różnicy energii wewnątrz metalu i energii zużytkowanej na pokonanie bariery potencjału. Prędkości początkowe z jakimi elektrony opuszczają metal, różnią się pomiędzy sobą zarówno pod względem kierunku jak i wartości. Średnia energia początkowa elektronów wynosi

a więc zależy jedynie od temperatury ciała emitującego.

Emisja fotoelektronowa (zewnętrzne zjawisko fotoelektryczne) występuje wskutek pochłaniania przez dane ciało energii promieniowania elektromagnetycznego, a w szczególności promieniowania świetlnego. Energia promieniowania jest pochłaniana w postaci oddzielnych kwantów, czyli fotonów. Energia fotonu jest proporcjonalna do częstości drgań świetlnych ν i równa się

Współczynnikiem proporcjonalności jest stała Plancka h = 6,625×10^-34 Js. Wskutek absorpcji fotonu elektron może uzyskać energię potrzebną do pokonania bariery potencjału. Warunkiem tego jest, aby energia fotonu była większa od pracy wyjścia elektronu z danej substancji. Wynika stąd, że emisja fotoelektronowa występuje przy promieniowaniu o częstotliwości wyższej od tzw. częstotliwości progowej. Długość fali odpowiadająca częstotliwości progowej nazywamy progiem falowym. Promieniowanie o częstotliwości mniejszej od częstotliwości progowej nie może wywołać emisji elektronowej, ponieważ energie fotonów są zbyt małe. Dla większości czystych metali próg falowy znajduje się poza zakresem widzialnym, w zakresie nadfioletu. Dla metali alkalicznych, odznaczających się najmniejszymi wartościami pracy wyjścia, próg falowy przypada w pobliżu środka zakresu widzialnego

Ten rodzaj emisji jest wykorzystywany w lampach fotoelektronowych, np. w fotodiodach.

Emisja wtórna jest to emisja zachodząca wskutek bombardowania danego ciała (metalu, półprzewodnika lub nawet dielektryka) elektronami lub jonami. Nazwa „emisja wtórna” pochodzi stąd, że do wywołania jej konieczne jest pierwotne źródło elektronów lub jonów. Elektrony bombardujące, zwane elektronami pierwotnymi, wnikają w głąb ciała bombardowanego i stopniowo przekazują swą energię napotkanym po drodze elektronom, umożliwiając niektórym z nich pokonanie bariery potencjału i wydostanie się na zewnątrz. Część elektronów pierwotnych zostaje odbita od powierzchni ciała bombardowanego. Elektrony wytrącone z danego ciała oraz elektrony odbite od jego powierzchni obejmujemy wspólną nazwą elektronów wtórnych. Stosunek ilości elektronów wtórnych do elektronów pierwotnych nazywamy współczynnikiem emisji wtórnej. Zwykle współczynnik ten wyrażamy jako stosunek gęstości prądu wtórnego do pierwotnego.

Współczynnik emisji wtórnej zależy od rodzaju materiału oraz od energii i kąta padania elektronów pierwotnych. Współczynnik δ wzrasta początkowo szybko, następnie osiąga maksimum i dalej powoli maleje. Początkowy szybki wzrost jest łatwy do wytłumaczenia. Ze wzrostem energii elektronów pierwotnych rośnie mianowicie liczba elektronów, które uzyskały dodatkową energię, a zatem zwiększa się emisja. Jednakże po przekroczeniu pewnej wartości napięcia współczynnik δ zaczyna się zmniejszać. Dzieje się tak wskutek tego, że ze wzrostem napięcia zwiększa się głębokość wnikania elektronów pierwotnych. Elektrony w ciele bombardowanym uzyskują więc wprawdzie większą energię, ale znaczna ich ilość znajduje się w głębi danego ciała i wskutek zderzeń albo nie dochodzi do jego powierzchni, albo też dochodzi ale z energią niedostateczną do pokonania bariery potencjału.

Emisja polowa jest to emisja elektronów zachodząca pod działaniem bardzo silnego pola elektrycznego. Zewnętrzne przyspieszające pole elektryczne ułatwia elektronom wydostanie się z metalu, co można interpretować jako obniżenie bariery potencjału. Pod wpływem tego pola zmniejsza się również szerokość bariery potencjału, a przy dostatecznie dużym natężeniu pola bariera ta staje się tak cienka, że mogą przez nią przenikać nawet elektrony o stosunkowo małych energiach. Zależność emisji polowej od natężenia pola elektrycznego jest analogiczne do zależności emisji termoelektronowej od temperatury.

4. Teoria diody, rodzaje katod, kontaktowa różnica potencjału.

Emisję elektronową wykorzystują lampy elektronowe zwane potocznie diodą. Dioda zawiera katodę stanowiącą źródło elektronów i anodę, do której pod wpływem przyłączonego napięcia dolatują elektrony emitowane przez katodę. Ruch elektronów w lampie powoduje w obwodzie anodowym przepływ prądu elektrycznego, zwanego prądem anody. Natężenie tego prądu jest zależne od napięcia anody (tj. napięcia występującego pomiędzy anodą a katodą) oraz w ogólnym przypadku - od emisji katody. Na rys. 4 została przedstawiona zależność prądu anody I od napięcia anody U przy stałej temperaturze katody tj. przy stałej wartości żarzenia, zwana charakterystyką diody.

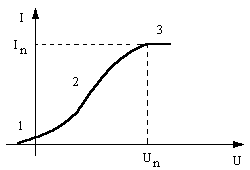
Rys. 4. Charakterystyka diody

1 - zakres prądu początkowego;

2 - zakres ładunku przestrzennego;

3 - zakres nasycenia.

Ze względu na zjawiska fizyczne zachodzące w diodzie, można charakterystykę jej podzielić na następujące zakresy:

• zakres I, zwany zakresem prądu początkowego, obejmujący ujemne napięcia anody;

• zakres II, zwany zakresem ładunku przestrzennego, obejmujący dodatnie napięcia anody mniejsze od napięcia nasycenia (U_n);

• zakres III, zwany zakresem nasycenia, obejmujący napięcia anody większe od napięcia nasycenia.

Prąd początkowy powstaje wskutek tego, że elektrony opuszczają katodę z pewną prędkością początkową. Dzięki temu część z nich może dotrzeć do anody pomimo ujemnego potencjału. Prąd anody jest zwykle niewielki i szybko maleje w miarę zmniejszana napięcia anody.

W zakresie ładunku przestrzennego prąd anody jest mniejszy od prądu nasycenia wskutek hamującego oddziaływania tego ładunku. Silne zagęszczenie elektronów wokół katody sprawia, że występujące tam pole elektryczne oddziałuje hamująco na ruch elektronów w kierunku anody. Część emitowanych elektronów o niewielkich prędkościach początkowych zostaje zahamowana w tym polu i zawrócona ku katodzie. Pozostała część, zależna od napięcia anody dociera do tej elektrody.

Jeżeli do anody przyłożymy dodatnie napięcie, spowodujemy przepływ elektronów otaczających katodę do anody, co powoduje zmniejszenie potencjału hamującego i w rezultacie wzrost prądu anody. Jeżeli przyłożymy wystarczająco duże napięcie zwane napięciem nasycenia, prąd anody osiągnie wartość równą prądowi emisyjnemu katody. Napięcie większe od napięcia nasycenia nie może spowodować wzrostu prądu anody, bowiem już przy napięciu nasycenia wszystkie elektrony emitowane przez katodę brały udział w przepływie prądu.

W lampach elektronowych stosowane są następujące podstawowe rodzaje termokatod:

• katody metalowe jednorodne,

• katody metalowe aktywowane,

• katody tlenkowe.

Do wyrobu katod jednorodnych (tzn. katod wykonanych z czystego metalu) stosowany jest prawie wyłącznie wolfram. Metal ten ma stosunkowo duży potencjał wyjścia (4,54V), ale jednocześnie odznacza się on bardzo wysoką temperatura topnienia (powyżej 3600 K) i małą szybkością parowania. Dzięki tym właściwościom może on pracować w wysokich temperaturach koniecznych do uzyskania dostatecznej emisji termoelektronowej. Ten rodzaj termokatod jest obecnie rzadko stosowany, wymagają one bowiem znacznej mocy do utrzymania ich wysokiej temperatury roboczej.

Katody metalowe aktywowane są wykonane w postaci rdzenia metalowego (najczęściej wolframowego) pokrytego jednoatomową warstwą metalu o mniejszej pracy wyjścia. Jako metal aktywujący stosowany jest najczęściej tor. Elektrony walencyjne atomów toru przechodzą częściowo do podłoża wolframowego, wskutek czego atomy toru przekształcają się w dodatnie jony przytrzymywane siłami elektrostatycznymi na powierzchni ujemnie naładowanego wolframu. Obecność tych jonów na powierzchni katody zmienia rozkład potencjału na granicy metal - próżnia, obniżając występującą tam barierę potencjału.

Katody tlenkowe wykonane są w postaci rdzenia metalowego (najczęściej niklowego), pokrytego warstwą tlenków metali ziem alkalicznych (baru, strontu, wapnia). Katody te odznaczają się bardzo dobrymi właściwościami i dlatego są stosowane w znacznej większości lamp elektronowych.

W każdym z metali jest ustalony poziom Fermiego. Przy zetknięciu dwóch różnych metali o różnych pracach wyjścia powstaje kontaktowa różnica potencjału (między powierzchniami stykających się metali). Przy takim zbliżeniu elektrony z metalu o wyższej energii Fermiego (mniejsza praca wyjścia), poprzez efekt tunelowania przechodzą przez barierę potencjału między powierzchniami metali do metalu o niższej energii Fermiego (większa praca wyjścia), oddając część energii bądź wykorzystując ją na tunelowanie. Stanie się tak ponieważ układ dąży do minimalizacji energii. Po pewnym czasie elektrony przestaną się przemieszczać a poziomy Fermiego wyrównają się. W tym czasie między powierzchniami będzie się wytwarzać pole elektryczne spowodowane nadmiarem elektronów w jednym metalu a ich niedoborem w drugim. Pole to może powodować zawracanie elektronów do wnętrza metalu, z którego wyszły.

5. Metody badawcze rozkładu prędkości elektronów.

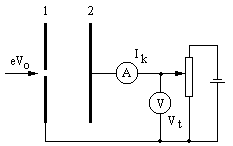
Metod pola hamującego. Istota tej metody polega na określeniu energii naładowanych cząstek według maksymalnej wartości bariery potencjału, która one mogą pokonać poruszając się w hamującym polu elektrycznym. Zasadę działania analizatora energii z jednorodnym polem wyjaśnia schemat:

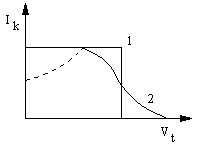
Przyrząd składa się z równoległych płytek 1 i 2, do których jest przyłożona różnica potencjałów V_t. W płytce 1 znajduje się mały otworek, przez który wchodzą do analizatora badane cząstki. Płytka 2 pełni funkcję kolektora elektronów. Jeśli w hamujące pole przyrządu wpada strumień elektronów przyśpieszonych różnicą potencjałów V₀ > V_t, to cząstki dosięgną kolektora i utworzą w jego obwodzie prąd I_k. Przy V₀ < V_t prąd w obwodzie kolektora jest równy zeru. Jeżeli prędkości początkowe elektronów w wiązce są równoległe do osi analizatora, to zależność prądu kolektora do napięcia hamującego, nazywana zwykle krzywa hamowania, powinna mieć wygląd idealnie równego schodka 1 (wykres powyżej). Po sporządzeniu krzywej hamowania i określeniu V = V₀, przy którym prąd kolektora spada do zera, można znaleźć energię badanych cząstek, równą w danym wypadku W₀ = eV₀. Jeśli strumień nie jest monokinetyczny, to krzywa hamowania odbiega od przebiegu 1 i może mieć kształt krzywej 2 (wykres powyżej).

W ogólnym przypadku prąd kolektora I_k jest związany z funkcją rozkładu energetycznego elektronów f(E) wyrażeniem:

(1)

gdzie s - powierzchnia poprzecznego przekroju wiązki, n - liczba elektronów w jednostce objętości.

Dlatego krzywa hamowania, wyrażająca związek między napięciem hamującym na kolektorze, a całkowitą ilością elektronów, których prędkość (w woltach) jest większa lub równa temu napięciu, jest równa całce rozkładu. Z powyższego wzoru wynika:

(2)

Po prawej stronie równania znajduje się wyrażenie określające przyrost prądu przypadający na przedział energii dE. Ilość elektronów w tym przedziale jest równa

(3)

Stąd

(4)

Porównując (2) i (4) otrzymujemy

W ten sposób różniczkując krzywą hamowania można określić funkcję rozkładu energii, to jest względna liczbę cząstek, przypadających na przedział nierozróżnialny energii. Różniczkowanie krzywej hamowania można realizować graficznie lub przy pomocy obwodów elektrycznych. Obydwie metody wnoszą do pomiarów określone błędy. Graficzne różniczkowanie krzywej hamowania nastręcza wiele trudności i jest związane z wprowadzeniem znacznych błędów. Dlatego lepiej jest stosować różniczkowanie elektroniczne, które zwiększa dokładność o 15 - 20 %.

Metoda elektronicznego różniczkowania polega na modulowaniu analizowanej energii i synchronicznym pomiarze prądu wyjściowego. Między anodę i katodę można przyłożyć regulowane napięcie stałe U_a i napięcie modulujące
wytwarzane przez generator. k jest dużo mniejsze od U_a. Wówczas prąd anodowy I_a jest funkcją napięcia (U_a + ∆U_a). Funkcję tę można rozwinąć w szereg Taylora:

gdzie prim oznacza różniczkowanie po U_a. Wstawiając za
, przegrupowując wyrazy i pomijając wyrazy dające mały wkład do rozwinięcia otrzymamy:

Do prądu anodowego daje więc wkład pewna składowa I₀ zależna tylko od stałego napięcia U_a i pewien człon zależny od sin ωt, trzeci człon możemy pominąć gdyż trzecia harmoniczna sygnału modulującego jest bardzo mała i nie ma wpływu na poszukiwaną wartość I'_a, która jest proporcjonalna do sinωt. Stąd wniosek, że należy wybrać z prądu anodowego składową o częstości ω, wzmocnić ją i zarejestrować.

II. LITERATURA.

Przy pisaniu części teoretycznej korzystałam z następujących pozycji:

• Jan Hennel „Lampy elektronowe”,

• C. Kittel „Wstęp do fizyki ciała stałego”,

• Ludomir Kalinowski „Fizyka metali”,

• H. Ibach, H. Lüth „Fizyka ciała stałego”,

• Tadeusz Marcinow „Ćwiczenia laboratoryjne z fizyki”.

III. WYKONANIE ĆWICZENIA.

Pierwszą czynnością jaką wykonałem na stanowisku pomiarowym było sprawdzenie połączenia układu według zamieszczonego poniżej schematu:

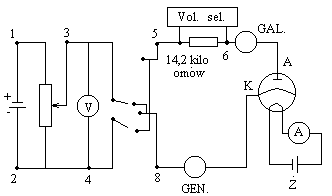
Schemat połączenia układu

GEN. - generator,

GAL. - galwanometr,

Vol. sel. - woltomierz selektywny.

Następnie, po spisaniu czułości mierników, klas i zakresów, przystąpiłem do właściwych pomiarów. Moim zadaniem było zdjęcie charakterystyki I_a = f(U_a) i N'(eU_a) = f(U_a) dla trzech wartości prądów żarzenia obu lamp znajdujących się na stanowisku pomiarowym. Na początku pomiarów ustaliłem k, czyli amplitudę zmiennego napięcia podawanego z generatora oraz ustawiłem taką samą częstotliwość ω na woltomierzu selektywnym (woltomierz ten mierzył jedynie sygnał o ustalonej częstotliwości, pozostałe pomijał i nie mierzył ich wartości). Kolejną czynnością było wywołanie termoemisji z katody poprzez doprowadzenie prądu żarzenia ze źródła Ż, mierzonego na amperomierzu. Aby zdjąć wymagane w ćwiczeniu charakterystyki, po odczekaniu krótkiego okresu czasu aby w lampie ustalił się prąd, zmieniałem stałe (regulowane) napięcie. Jego wartość odczytywałem na woltomierzu, jednocześnie odczytywałem wskazania z galwanometru (charakterystyka I_a = f(U_a)) oraz woltomierza selektywnego (charakterystyka N'(eU_a) = f(U_a)). W przypadku pierwszej lampy, którą była lampa z katodą wolframową, napięcie zmieniałem od ujemnego (przy którym nie pojawiał się jeszcze prąd anodowy) wzwyż, po dojściu do napięcia równego 0 zmieniałem polaryzację i dalej zwiększałem napięcie aż do momentu osiągnięcia końca skali miernika napięcia lub natężenia. Pomiary te powtarzałem dla trzech różnych wartości prądu żarzenia. Następnie po wpięciu w układ lampy z katodą tlenkową w miejsce poprzedniej lampy, przeprowadziłem podobne pomiary. Jednak w przypadku lampy z katodą tlenkową nie musiałem już zmieniać napięcia od ujemnego wzwyż, a jedynie od 0.

IV. OPRACOWANIE WYNIKÓW I BŁĘDY.

Amplituda zmiennego napięcia dla wszystkich pomiarów wynosiła , a częstotliwość 170 Hz.

Musiałem zdjąć charakterystyki dla trzech prądów żarzenia. Aby były one dobrze widoczne na wykresach, które sporządziłem używając wyników znajdujących się w tabelach umieszczonych na następnych stronach zmieniałem zakresy mierników. Tabele zawierają już przeliczone wartości (zakres * odczytana liczba podziałek / skale). Przy każdej tabeli podam dokładne ich zakresy, liczbę podziałek oraz prąd żarzenia. Dodatkowa umieszczę pod każdą tabelą wykresy charakterystyk oraz policzę błędy mierników.

Lampa z katodą wolframową.

Prąd żarzenia 1300 mA.

Opis mierników (zakresy, skale):

• zakres woltomierza napięcia stałego, regulowanego napięcia - 7,5 [V], skala 0 - 30;

• zakres woltomierza selektywnego - 3[V], skala 0 - 3;

• zakres galwanometru - 2 [μA], skala 0 - 100.

Pierwsza kolumna w tabeli oznacza stałe, regulowane napięcie; druga N'(eU); trzecia natężenie prądu anody (mik. A oznacza μA) natomiast czwarta ln policzony z tego prądu. W celu zmniejszenia zajmowanego miejsca przez tabele podzieliłem pomiary na dwie części i umieściłem je obok siebie.

U [V]	N'(eU) [V]	I [mik. A]	Ln I [mik. A]	U [V]	N'(eU) [V]	I [mik. A]	Ln I [mik. A]
-2,5	0,25	0	-	0,5	0,4	0,68	-0,386
-2,25	0,35	0,02	-3,912	0,625	0,4	0,7	-0,357
-2,125	0,6	0,04	-3,219	0,75	0,35	0,7	-0,357
-2	0,85	0,06	-2,813	0,875	0,35	0,72	-0,329
-1,875	1,15	0,1	-2,303	1	0,35	0,72	-0,329
-1,75	1,4	0,14	-1,966	1,125	0,35	0,74	-0,301
-1,625	1,7	0,19	-1,661	1,25	0,3	0,74	-0,301
-1,5	1,75	0,24	-1,427	1,5	0,3	0,76	-0,274
-1,375	1,7	0,29	-1,238	1,75	0,3	0,78	-0,248
-1,25	1,55	0,34	-1,079	2	0,3	0,8	-0,223
-1,125	1,3	0,4	-0,916	2,25	0,3	0,81	-0,211
-1	1,1	0,44	-0,821	2,5	0,3	0,82	-0,198
-0,875	1	0,48	-0,734	2,75	0,3	0,84	-0,174
-0,75	0,85	0,5	-0,693	3	0,25	0,84	-0,174
-0,625	0,7	0,54	-0,616	3,25	0,25	0,86	-0,151
-0,5	0,65	0,56	-0,580	3,75	0,25	0,88	-0,128
-0,375	0,6	0,58	-0,545	4,25	0,25	0,9	-0,105
-0,25	0,55	0,6	-0,511	4,75	0,25	0,92	-0,083
-0,125	0,5	0,61	-0,494	5,25	0,25	0,94	-0,062
0	0,5	0,62	-0,478	5,75	0,25	0,96	-0,041
0,125	0,5	0,64	-0,446	6,75	0,25	0,98	-0,020
0,25	0,4	0,66	-0,416	7,5	0,25	1	0,000
0,375	0,4	0,67	-0,400

Błędy:

Błąd miernika na którym odczytywałem natężenie prądu żarzenia:

Jak widać z obliczeń błędy są zbyt małe aby naniesione na wykres były widoczne. Można przyjąć, że są one wliczone w rozmiar punktów pomiarowych.

Prąd żarzenia 1250 [mA]

Opis mierników:

• zakres woltomierza napięcia stałego, regulowanego - 7.5 [V], skala 0 - 30;

• zakres woltomierza selektywnego 1 [V], skala 0 - 3;

• zakres galwanometru 1 [μA]; skala 0 - 100.

U [V]	N'(eU) [V]	I [mik. A]	Ln I [mik. A]	U [V]	N'(eU) [V]	I [mik. A]	Ln I [mik. A]
-2,5	0,233	0	-	-0,125	0,300	0,22	-1,514
-2,125	0,283	0,01	-4,605	0	0,300	0,22	-1,514
-2	0,317	0,02	-3,912	0,125	0,300	0,23	-1,470
-1,875	0,433	0,03	-3,507	0,375	0,300	0,24	-1,427
-1,75	0,533	0,04	-3,219	0,625	0,283	0,25	-1,386
-1,625	0,600	0,055	-2,900	0,875	0,267	0,26	-1,347
-1,5	0,700	0,08	-2,526	1,125	0,267	0,27	-1,309
-1,375	0,700	0,095	-2,354	1,5	0,250	0,28	-1,273
-1,25	0,667	0,11	-2,207	2	0,250	0,29	-1,238
-1,125	0,600	0,135	-2,002	2,5	0,250	0,3	-1,204
-1	0,533	0,15	-1,897	3	0,250	0,31	-1,171
-0,875	0,450	0,175	-1,743	3,625	0,233	0,32	-1,139
-0,75	0,400	0,18	-1,715	4,25	0,233	0,33	-1,109
-0,625	0,383	0,19	-1,661	5	0,233	0,34	-1,079
-0,5	0,350	0,2	-1,609	5,875	0,233	0,35	-1,050
-0,375	0,333	0,205	-1,585	7,125	0,233	0,36	-1,022
-0,25	0,317	0,21	-1,561

Błędy:

Reszta błędów jest taka sama jak powyżej i również są one zbyt małe aby nanosić je na wykresy.

Prąd żarzenia 1400 [mA].

Opis mierników:

• zakres woltomierza stałego, regulowanego napięcia - 7,5 [V], skala 0 - 30;

• zakres woltomierza selektywnego - 10 [V], skala 0 - 3;

• zakres galwanometru - 5 [μA], skala 0 - 100.

U [V]	N'(eU) [V]	I [mik. A]	Ln I [mik. A]	U [V]	N'(eU) [V]	I [mik. A]	Ln I [mik. A]
-3	0,333	0	-	0,5	1,167	2,1	0,742
-2,5	0,667	0,05	-2,996	0,75	1,000	2,15	0,765
-2,25	1,333	0,1	-2,303	0,875	1,000	2,2	0,788
-2,125	2,167	0,175	-1,743	1,125	0,833	2,25	0,811
-2	3,000	0,275	-1,291	1,25	0,833	2,3	0,833
-1,875	4,000	0,4	-0,916	1,5	0,833	2,35	0,854
-1,75	4,833	0,525	-0,644	1,75	0,667	2,4	0,875
-1,625	5,333	0,7	-0,357	2	0,667	2,45	0,896
-1,5	5,333	0,85	-0,163	2,25	0,667	2,5	0,916
-1,375	5,000	1	0,000	2,5	0,667	2,55	0,936
-1,25	4,333	1,15	0,140	2,75	0,667	2,6	0,956
-1,125	3,667	1,3	0,262	3,125	0,667	2,65	0,975
-1	3,000	1,4	0,336	3,375	0,667	2,7	0,993
-0,875	2,667	1,5	0,405	3,75	0,667	2,75	1,012
-0,75	2,333	1,6	0,470	4,125	0,667	2,8	1,030
-0,625	2,000	1,65	0,501	4,5	0,667	2,85	1,047
-0,5	1,833	1,725	0,545	4,875	0,667	2,9	1,065
-0,375	1,667	1,8	0,588	5,375	0,500	2,95	1,082
-0,25	1,500	1,85	0,615	5,875	0,500	3	1,099
-0,125	1,333	1,9	0,642	6,375	0,500	3,05	1,115
0	1,333	1,9	0,642	7	0,333	3,1	1,131
0,125	1,333	1,975	0,681	7,5	0,333	3,15	1,147
0,25	1,500	2,025	0,706

Błędy:

Również w tym przypadku pozostałe błędy są takie same ja k wcześniej i nie można ich nanieść na wykresy.

Lampa z katodą tlenkową.

Prąd żarzenia 150 [mA].

Opis mierników:

• zakres woltomierza stałego, regulowanego napięcia - 7,5 [V], skala 0 - 30;

• zakres woltomierza selektywnego - 3 [V], skala 0 - 3;

• zakres galwanometru - 1 [μA], skala 0 - 100.

U [V]	N'(eU) [V]	I [mik. A]	Ln I [mik. A]	U [V]	N'(eU) [V]	I [mik. A]	Ln I [mik. A]
0	0,4	0	-	2,625	0,4	0,41	-0,892
0,5	0,4	0,01	-4,605	2,875	0,4	0,42	-0,868
0,625	0,7	0,04	-3,219	3,375	0,4	0,43	-0,844
0,75	1,5	0,09	-2,408	3,5	0,4	0,44	-0,821
0,875	1,85	0,14	-1,966	3,75	0,4	0,45	-0,799
1	1,9	0,18	-1,715	4,125	0,4	0,46	-0,777
1,125	1,75	0,22	-1,514	4,5	0,4	0,47	-0,755
1,25	1,2	0,275	-1,291	5	0,4	0,48	-0,734
1,375	0,55	0,33	-1,109	5,5	0,4	0,49	-0,713
1,625	0,45	0,36	-1,022	5,875	0,4	0,5	-0,693
1,75	0,4	0,37	-0,994	6,25	0,4	0,51	-0,673
1,875	0,4	0,38	-0,968	6,75	0,4	0,52	-0,654
2,125	0,4	0,39	-0,942	7,25	0,4	0,53	-0,635
2,375	0,4	0,4	-0,916

Błędy:

Błąd jaki mogłem popełnić przy odczycie prądu żarzenia:

Błąd miernika stałego, regulowanego napięcia jest taki sam jak w pozostałych przypadkach. Przy tych pomiarach podobnie jak poprzednio nie mogłem nanieść błędów na wykresy ponieważ są one zbyt małe.

Prąd żarzenia 155 [mA].

Opis mierników:

• zakres woltomierza stałego, regulowanego napięcia - 7,5 [V], skala 0 - 30;

• zakres woltomierza selektywnego - 3 [V], skala 0 - 3;

• zakres galwanometru - 1 [μA], skala 0 - 100.

U [V]	N'(eU) [V]	I [mik. A]	Ln I [mik. A]	U [V]	N'(eU) [V]	I [mik. A]	Ln I [mik. A]
0	0,4	0	-	2,5	0,4	0,38	-0,968
0,5	0,4	0,01	-4,605	2,75	0,4	0,39	-0,942
0,625	0,7	0,04	-3,219	3	0,4	0,4	-0,916
0,75	1,4	0,09	-2,408	3,25	0,4	0,41	-0,892
0,875	1,7	0,12	-2,120	3,75	0,4	0,42	-0,868
1	1,8	0,16	-1,833	4,125	0,4	0,43	-0,844
1,125	1,6	0,21	-1,561	4,625	0,4	0,44	-0,821
1,25	1,1	0,26	-1,347	5,125	0,4	0,45	-0,799
1,375	0,6	0,3	-1,204	5,625	0,4	0,46	-0,777
1,5	0,45	0,32	-1,139	6,125	0,4	0,47	-0,755
1,625	0,4	0,33	-1,109	6,625	0,4	0,48	-0,734
1,75	0,4	0,34	-1,079	7	0,4	0,49	-0,713
2	0,4	0,36	-1,022	7,5	0,4	0,5	-0,693
2,25	0,4	0,37	-0,994

Błędy:

Błędy przy tym pomiarze są identyczne jak przy poprzednim.

Na następnej stronie sprawozdania przedstawiłem dwa wspólne wykresy, na których umieściłem wszystkie charakterystyki. Na obu są u dołu serie. Ich kolory odpowiadają natężeniom prądu żarzenia. Kolory te na obu wykresach pokrywają się tzn. dany kolor oznacza ten sam prąd żarzenia na wykresach.

I tak:

• seria pierwsza w kolorze niebieskim odpowiada prądowi 1300 mA (lampa z katodą wolframową),

• seria druga w kolorze czerwonym odpowiada prądowi 1250 mA (lampa z katodą wolframową),

• seria trzecia w kolorze czarnym odpowiada prądowi 1400 mA (lampa z katodą wolframową),

• 
  seria czwarta w kolorze ciemno czerwonym odpowiada prądowi 150 mA (lampa z katodą tlenkową),

• 
  seria piąta w kolorze zielonym odpowiada prądowi 155 mA (lampa z katodą tlenkową).

Na obu wykresach łatwo zauważyć, że dwie ostatnie serie różnią się znacznie od trzech pierwszych. Różnica ta spowodowana jest tym, że trzy pierwsze serie odnoszą się do lampy z katodą wolframową, natomiast dwie ostatnie do lampy z katodą tlenkową.

Kolejnym moim zadaniem było korzystając ze sporządzonych wykresów odczytać kontaktową różnicę potencjałów dla obu lamp. Mogę to zrobić zarówno na podstawie wykresu przedstawiającego charakterystykę ln I = f(U) jak i na podstawie wykresu przedstawiającego rozkład energetyczny.

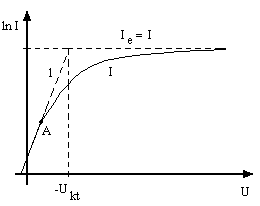
Aby z wykresu charakterystyki ln I = f(U) odczytać kontaktową różnicę potencjału należy przez początkowe punkty tej charakterystyki (kiedy punkty pomiarowe układają się w linię prosta - zależność liniowa) poprowadzić linię prostą - 1 (rys. obok). Dzięki temu otrzymamy krzywą przedstawiającą wynik oczekiwany. Zależność obserwowana w doświadczeniu pokrywa się z krzywą teoretyczną tylko do pewnego punktu A, dalej występuje odstępstwo od liniowej zależności (zakres ładunku przestrzennego). Znając prąd emisyjny katody I_e = I możemy wyznaczyć wartość napięcia kontaktowego: wartość odciętej -U punktu przecięcia prostej 1 z prostą odpowiadającą rzędnej I_e = I.

Korzystając z powyższej metody otrzymałem następujące wartości kontaktowej różnicy potencjałów:

• lampa z katodą wolframową U_kt = -1,4 V,

• lampa z katodą tlenkową U_kt = -0,85 V,

W przypadku rozkładu energetycznego wystarczy sprawdzić przy jakiej wartości stałego, regulowanego napięcia otrzymujemy maksymalną wartość N'(eU). Korzystając z wykresów umieszczonych pod każdą tabelą odczytałem kontaktową różnicę potencjałów U_kt dla obu lamp (dzięki temu, że prowadziłem pomiary przy kilku prądach żarzenia mogłem porównać otrzymane wartości).

Oto otrzymane wyniki:

• lampa z katodą wolframową Ukt = -1,5 V,

• lampa z katodą tlenkową U_kt = -1 V.

Na wykresie przedstawiającym wszystkie charakterystyki N'(eU) = f(U) widać, że wartość kontaktowej różnicy potencjałów dla różnych prądów żarzenia (ale tej samej lampy) jest taka sama.

Ostatnim moim zadaniem było obliczenie temperatury katody dla poszczególnych prądów żarzenia. Mogłem to uczynić korzystając ze wzoru:

gdzie: e - ładunek elementarny wynoszący 1,602 × 10^-19 [C],

k_B - stała Boltzmana wynosząca 1,38 × 10^-23,

a - tangens kąta nachylenia krzywej 1 (rysunek powyżej) odczytany z wykresu charakterystyki ln I = f(U). Oto otrzymane wyniki:

• lampa z katodą wolframową:

U_Ż = 1300 mA ,T = 2093,15 K;

U_Ż = 1250 mA, T = 2093,15 K;

U_Ż =1400 mA, T = 3475,77 K;

• lampa z katodą tlenkową:

U_Ż = 150 mA, T = 1046,57 K;

U_Ż = 155 mA, T = 1046,57 K;

Łatwo zauważyć, że w zarówno w przypadku lampy z katodą wolframową jak i lampy z katodą tlenkową dla dwóch różnych prądów żarzenia otrzymałem identyczne temperatury katody. Wynik ten mógł być rezultatem niedokładnego odczytania punktów pomiarowych z wykresu. Na pojawienie się identycznych temperatur dla lampy z katodą tlenkową mógł mieć również wpływ fakt, że pomiary były wykonywane przy niewielkiej różnicy prądów żarzenia.

V. WNIOSKI.

Na wykresach umieszczonych pod każdą tabelą oraz na wykresach wspólnych przedstawiłem charakterystyki wymagane w ćwiczeniu. W przypadku wspólnego wykresu dla charakterystyki N'(eU) = f(U) można na nim zauważyć, że maksimum rozkładu energetycznego zależy od prądu żarzenia. Przy wyższych prądach żarzenia maksimum jest również wyższe. Można również zauważyć, iż dla lampy tlenkowej (pomiary przy prądach żarzenia 150 mA i 155 mA) jest ono wyższe niż dla lampy wolframowej (pomiary przy prądach 1300 mA i 1250 mA). Widać wyraźnie więc, że lampy z katodą tlenkowa są skuteczniejsze od wolframowych ponieważ do podobnej emisji potrzebują o rząd niższego prądu żarzenia. Na wykresie tym można jeszcze zaobserwować, że wraz ze wzrostem prądu żarzenia wzrasta wartość napięcia kontaktowego. Na wykresach zależności ln I = f(U) można spostrzec, że w zakresie prądu początkowego potwierdza się zależność liniowa ln natężenia od napięcia. Po przekroczeniu tego zakresu charakterystyka staje się krzywoliniowa. Wykres ten uwidacznia również fakt, iż wraz ze wzrostem prądu żarzenia zwiększa się prąd nasycenia. Z obliczeń jakie przeprowadziłem wynika, że temperatura katody wzrasta wraz ze wzrostem prądu żarzenia. Co prawda dla dwóch różnych prądów w przypadku obu lamp otrzymałem takie same wartości ale mogło to być spowodowane niedokładnym odczytem punktów dla których występuje charakterystyka liniowa, bądź w przypadku lampy z katodą tlenkową małą różnicą prądów.

1

- 17 -

---