MATERIAŁY POMOCNICZE DO LABORATORIÓW

Z BADAŃ OPERACYJNYCH

Na zajęcia laboratoryjne należy przynieść dyskietkę i materiały pomocnicze.

Badania operacyjne: wybrane zagadnienia programowania liniowego - rozwiązywanie zadań z wykorzystaniem modułu Solver.

1. WYBÓR STRUKTURY ASORTYMENTOWEJ PRODUKCJI

Zad.1 str. 23. Badania operacyjne w przykładach i zadaniach pod red. K. Kukuły, PWN: Warszawa 2001.

Zakład produkuje dwa wyroby, które są wykonywane na dwóch obrabiarkach: O₁ oraz O₂ i na frezarce F. Czas pracy tych maszyn jest ograniczony i wynosi, odpowiednio, dla obrabiarki O₁ - 33 000 godz., dla obrabiarki O₂ - 13 000 godz. i dla frezarki - 80 000 godz. Zużycie czasu pracy maszyn (w godz.) na produkcję jednostki każdego z wyrobów podano w poniższej tabeli.

Maszyny	Zużycie czasu pracy na jednostkę wyrobu
		I	II
O1	3	1
O2	1	1
F	5	8

Zysk ze sprzedaży wyrobu I wynosi 1 zł, ze sprzedaży wyrobu II - 3 zł. Z analizy sprzedaży z lat ubiegłych wynika, że wyrobu II nie będzie można sprzedać więcej iż 7 000 szt.

Zaplanować strukturę asortymentową produkcji tak, aby przy przyjętych ograniczeniach zysk ze sprzedaży wyrobów był jak największy.

Rozwiąż zadanie programowania liniowego stosując moduł Solver /Excel/.

Postać standardowa modelu:

Fc: X1 + 3X2 → MAX

Wo. 3X1 + X2 ≤ 33 000 (1.)

X1 + X2 ≤ 13 000 (2.)

5X1 + 8X2 ≤ 80 000 (3.)

X2 ≤ 7 000 (4.)

Xi ≥ 0

Algorytm rozwiązania - moduł Solver /Excel/

1. Korzystamy z modelu decyzyjnego w postaci standardowej.

2. Otwieramy arkusz Excel-a, nazywamy go zad.1.Wprowadzamy dane w następujący sposób:

a/ współczynniki funkcji celu (wagi funkcji celu) w zakres: B3:C3,

b/ zmienne decyzyjne w zakres: B4:C4,

c/ wartości początkowe zmiennych decyzyjnych (dla każdej zmiennej wpisujemy wartość początkową 0) w zakres: B5:C5,

d/ współczynniki warunków ograniczających w zakres: B9:C12,

e/ wyrazy wolne warunków ograniczających w zakres: E9:E12,

f/ komórkę D5 przeznaczamy na wartość funkcji celu dla bieżących wartości zmiennych decyzyjnych; w komórce tej wprowadzamy funkcję Excel-a: SUMA.ILOCZYNÓW(B3:C3;B5:C5),

g/ w komórkach D9:D12 zapisujemy formuły obliczania wartości lewych stron warunków ograniczających zadania optymalizacyjnego dla bieżących wartości zmiennych decyzyjnych według wzoru D9:=SUMA.ILOCZYNÓW(B9:C9;$B$5:$C$5); (F4 - skrót klawiszowy wprowadzający adres bezwzględny). Formułę z komórki D9 kopiujemy do komórek D10, D11, D12.

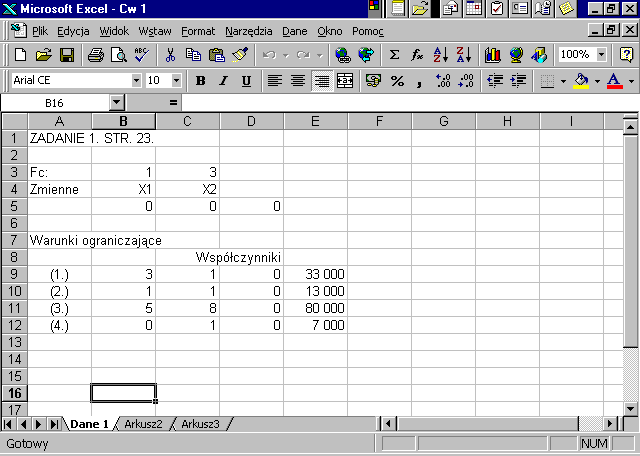
3. Wybieramy z menu Narzędzia opcję Solver. Wyświetli się okno dialogowe Solver - Parametry.

4. W okno Komórka celu wprowadzamy adres komórki z formułą obliczania wartości funkcji celu ($D$5).

5. Wybieramy jedno z kryteriów optymalizacji. W naszym zadaniu będzie to Maks.

6. 
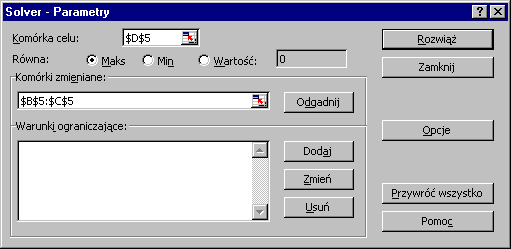
   W polu Komórki zmieniane wprowadzamy zakres komórek, w które wcześniej wpisaliśmy wartości zerowe zmiennych decyzyjnych ($B$5:$C$5).

7. W pole Warunki ograniczające za pomocą przycisku Dodaj wprowadzamy kolejne warunki ograniczające.

8. Otworzy się okno Dodaj warunek ograniczający. W polu Adres komórki wprowadzamy adres komórki zawierającej formułę obliczania wartości lewej strony pierwszego warunku ograniczającego ($D$9), następnie wybieramy symbol właściwej relacji (<=), a w polu Warunek ograniczający wprowadzamy adres komórki zawierającej wartość wyrazu wolnego pierwszego warunku ograniczającego ($E$9). W analogiczny sposób dodajemy kolejne warunki ograniczające.

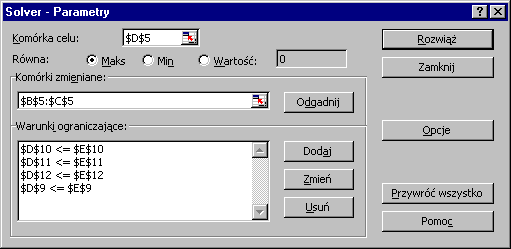
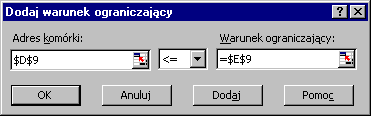
9. Po wprowadzeniu ostatniego warunku ograniczającego klikamy OK i wracamy do okna Solver - Parametry.

1. 
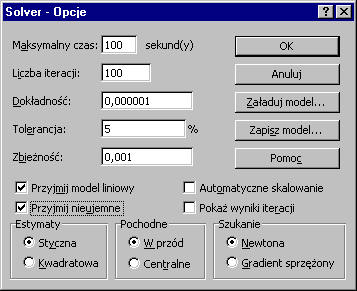
   Klikamy w oknie dialogowym w Opcje i zaznaczamy: Przyjmij model liniowy oraz Przyjmij nieujemne (warunek nieujemności zmiennych decyzyjnych - X_j ≥ 0). Potwierdzamy polecenie OK.

9. 
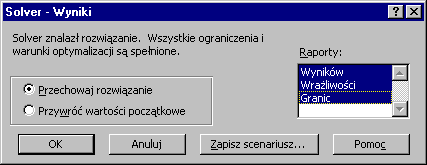
   W oknie Solver - Parametry klikamy przycisk Rozwiąż i otrzymujemy okno dialogowe, w którym zaznaczamy raporty: Wyników, Wrażliwości i Granic.

10. 
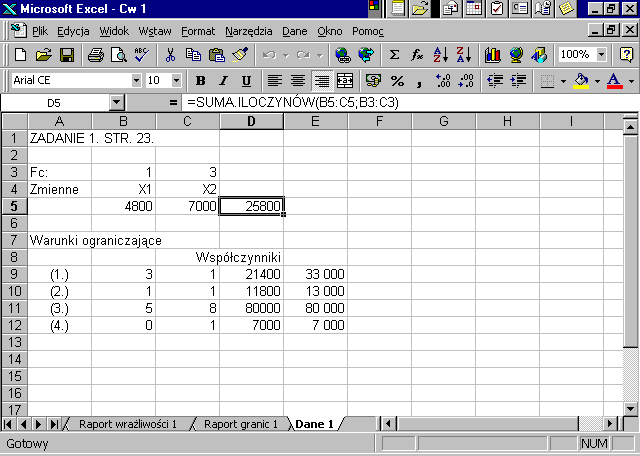
    Rozwiązanie zadania otrzymujemy zarówno w arkuszu, w którym wprowadzaliśmy dane jak i w Raporcie wyników.

11. Sprawdźmy jeszcze, wykorzystując raporty wyników i wrażliwości w Solverze, czy otrzymane rozwiązanie jest jedynym rozwiązaniem optymalnym:

a/ jeżeli w raporcie wrażliwości wartość końcowa i przyrost krańcowy zmiennej decyzyjnej są równe zero to występuje nieskończenie wiele rozwiązań optymalnych,

b/ jeżeli zależności te dla zmiennych decyzyjnych nie są spełnione, to dla każdego warunku ograniczającego sprawdzamy wartość ceny dualnej:

• jeżeli przynajmniej w jednym przypadku cena dualna jest równa zero i

• odpowiedni warunek ograniczający jest wiążący (w raporcie wyników) to zadanie ma nieskończenie wiele rozwiązań optymalnych.

Microsoft Excel 8.0a Raport wyników
Komórka celu (Maks)
	Komórka	Nazwa	Wartość początkowa	Wartość końcowa
	$D$5		0	25800
Komórki decyzyjne
	Komórka	Nazwa	Wartość początkowa	Wartość końcowa
	$B$5	X1	0	4800
	$C$5	X2	0	7000
Warunki ograniczające
	Komórka	Nazwa	Wartość komórki	formuła	Status	Luz
	$D$9	(1.) Współczynniki	21400	$D$9<=$E$9	Nie wiążące	11600
	$D$10	(2.) Współczynniki	11800	$D$10<=$E$10	Nie wiążące	1200
	$D$11	(3.) Współczynniki	80000	$D$11<=$E$11	Wiążące	0
	$D$12	(4.) Współczynniki	7000	$D$12<=$E$12	Wiążące	0

Microsoft Excel 8.0a Raport wrażliwości
Komórki decyzyjne
			Wartość	Przyrost	Współczynnik	Dopuszczalny	Dopuszczalny
	Komórka	Nazwa	końcowa	krańcowy	funkcji celu	wzrost	spadek
	$B$5	X1	4800	0	1	0,875	1
	$C$5	X2	7000	0	3	1E+30	1,4
Warunki ograniczające
			Wartość	Cena	Prawa strona	Dopuszczalny	Dopuszczalny
	Komórka	Nazwa	końcowa	dualna	w. o.	wzrost	spadek
	$D$9	(1.) Współczynniki	21400	0	33000	1E+30	11600
	$D$10	(2.) Współczynniki	11800	0	13000	1E+30	1200
	$D$11	(3.) Współczynniki	80000	0,2	80000	6000	24000
	$D$12	(4.) Współczynniki	7000	1,4	7000	3000	2000

Microsoft Excel 8.0a Raport granic
		Cel	Wartość
	Komórka	Nazwa	końcowa
	$D$5		25800
		Zmienne decyzyjne	Wartość		Dolna	Cel		Górna	Cel
	Komórka	Nazwa	końcowa		granica	Wynik		granica	Wynik
	$B$5	X1	4800		0	21000		4800	25800
	$C$5	X2	7000		0	4800		6999,999859	25799,99958

W związku z tym, że dla rozwiązywanego zadania nie są spełnione wymienione warunki istnieje tylko jedno rozwiązanie optymalne.

Rozwiązanie:

X1 = 4800 szt.

X2 = 7000 szt.

Fc. = 25 800 zł

2. PROBLEM MIESZANKI

Rozwiąż zadanie stosując moduł Solver.

Zadanie 2.

Racjonalna hodowla Pokėmonów wymaga dostarczenia dziennie każdemu osobnikowi trzech składników odżywczych A, B i C w następujących ilościach: składnika A co najmniej 4 jednostki wagowe; składnika B dokładnie 4 jednostki, a składnika C co najwyżej 6 jednostek wagowych. Składniki te zawarte są w trzech rodzajach galaretek tazos: czarnej, niebieskiej oraz fioletowej. W poniższej tablicy podano zawartość każdego ze składników w 1kg galaretki oraz ceny zakupów tych galaretek.

Zawartość składnika w 1 kg galaretki	Galaretki			Dzienna norma zapotrzebowania
		Czarna	Niebieska		Fioletowa
A	1	1	3	4
B	2	1	1	4
C	0	2	3	6
CENA	2	2	1

Jakie ilości poszczególnych galaretek należy zakupić, aby dzienne koszty wyżywienia Pokėmonów były możliwie najniższe?

Algorytm rozwiązania - moduł Solver /Excel/.

Postać standardowa modelu:

Fc: 2X1 + 2X2 + X3 → MIN

Wo. X1 + X2 + 3X3 ≥ 4 (1.)

2X1 + X2 + X3 = 4 (2.)

2X2 + 3X3 ≤ 6 (3.)

Xi ≥ 0

1. Korzystamy z modelu decyzyjnego w postaci standardowej.

2. Otwieramy nowy arkusz Excel-a, nazywamy go zad.2. Wprowadzamy dane w następujący sposób:

a/ współczynniki funkcji celu (wagi funkcji celu) w zakres: C2:E2,

b/ zmienne decyzyjne w zakres: C3:E3,

c/ wartości początkowe zmiennych decyzyjnych (dla każdej zmiennej wpisujemy wartość początkową 0) w zakres: C4:E4,

d/ współczynniki warunków ograniczających w zakres: C7:E9,

e/ wyrazy wolne warunków ograniczających w zakres: G7:G9,

f/ komórkę F4 przeznaczamy na wartość funkcji celu dla bieżących wartości zmiennych decyzyjnych; w komórce tej wprowadzamy funkcję Excel-a: =SUMA.ILOCZYNÓW(C2:E2;C4:E4),

g/ w komórkach F7:F9 zapisujemy formuły obliczania wartości lewych stron warunków ograniczających zadania optymalizacyjnego dla bieżących wartości zmiennych decyzyjnych według wzoru F7: =SUMA.ILOCZYNÓW(C7:E7;$C$4:$E$4); formułę z komórki F7 kopiujemy do komórek F8, F9.

3. Wybieramy z menu Narzędzia opcję Solver. Wyświetli się okno dialogowe Solver - Parametry.

4. W okno Komórka celu wprowadzamy adres komórki z formułą obliczania wartości funkcji celu ($F$4).

5. Wybieramy jedno z kryteriów optymalizacji. W naszym zadaniu będzie to Min.

6. W polu Komórki zmieniane wprowadzamy zakres komórek, w które wcześniej wpisaliśmy wartości zerowe zmiennych decyzyjnych ($C$4:$E$4).

7. W pole Warunki ograniczające za pomocą przycisku Dodaj wprowadzamy kolejne warunki ograniczające.

8. Otworzy się okno Dodaj warunek ograniczający. W polu Adres komórki wprowadzamy adres komórki zawierającej formułę obliczania wartości lewej strony pierwszego warunku ograniczającego ($F$7), następnie wybieramy symbol właściwej relacji (>=), a w polu Warunek ograniczający wprowadzamy adres komórki zawierającej wartość wyrazu wolnego pierwszego warunku ograniczającego ($G$7). W analogiczny sposób dodajemy kolejne warunki ograniczające.

9. 
   Po wprowadzeniu ostatniego warunku ograniczającego klikamy OK i wracamy do okna Solver - Parametry.

10. Klikamy w oknie dialogowym w Opcje i zaznaczamy: Przyjmij model liniowy oraz Przyjmij nieujemne (warunek nieujemności zmiennych decyzyjnych - X_j ≥ 0), potwierdzamy OK.

11. W oknie Solver - Parametry klikamy przycisk Rozwiąż i otrzymujemy okno dialogowe, w którym zaznaczamy raporty: Wyników, Wrażliwości i Granic.

12. Rozwiązanie zadania otrzymujemy zarówno w arkuszu, w którym wprowadzaliśmy dane jak i w Raporcie wyników.

13. Sprawdzamy, czy uzyskane rozwiązanie optymalne jest jedynym rozwiązaniem, czy też jest jednym z nieskończenie wielu rozwiązań optymalnych.

A/ Jeżeli w raporcie wrażliwości wartość końcowa i przyrost krańcowy zmiennej decyzyjnej są równe zero to występuje nieskończenie wiele rozwiązań optymalnych.

B/ Jeżeli zależności te dla zmiennych decyzyjnych nie są spełnione, to dla każdego warunku ograniczającego sprawdzamy wartość ceny dualnej:

1. jeżeli przynajmniej w jednym przypadku cena dualna jest równa zero i

2. odpowiedni warunek ograniczający jest wiążący (w raporcie wyników) to zadanie ma nieskończenie wiele rozwiązań optymalnych,

W związku z tym, że dla pierwszego warunku ograniczającego cena dualna jest równa zero, a warunek jest wiążący istnieje nieskończenie wiele rozwiązań optymalnych.

Microsoft Excel 8.0a Raport wrażliwości
Komórki decyzyjne
			Wartość	Przyrost	Współczynnik	Dopuszczalny	Dopuszczalny
	Komórka	Nazwa	końcowa	krańcowy	funkcji celu	wzrost	spadek
	$B$4	x1	1,6	0	2	0	1E+30
	$C$4	x2	0	1	2	1E+30	1
	$D$4	x3	0,8	0	1	5	0
Warunki ograniczające
			Wartość	Cena	Prawa strona	Dopuszczalny	Dopuszczalny
	Komórka	Nazwa	końcowa	dualna	w. o.	wzrost	spadek
	$E$6		4	0	4	3	2
	$E$7		4	1	4	4	2,666666667
	$E$8		2,4	0	6	1E+30	3,6

Microsoft Excel 8.0a Raport wyników
Komórka celu (Min)
	Komórka	Nazwa	Wartość początkowa	Wartość końcowa
	$E$4		0	4
Komórki decyzyjne
	Komórka	Nazwa	Wartość początkowa	Wartość końcowa
	$B$4	x1	0	1,6
	$C$4	x2	0	0
	$D$4	x3	0	0,8
Warunki ograniczające
	Komórka	Nazwa	Wartość komórki	formuła	Status	Luz
	$E$6		4	$E$6>=$F$6	Wiążące	0
	$E$7		4	$E$7=$F$7	Wiążące	0
	$E$8		2,4	$E$8<=$F$8	Nie wiążące	3,6

Microsoft Excel 8.0a Raport granic
		Cel	Wartość
	Komórka	Nazwa	końcowa
	$F$4		4
		Zmienne decyzyjne	Wartość		Dolna	Cel		Górna	Cel
	Komórka	Nazwa	Końcowa		granica	Wynik		granica	Wynik
	$C$4	x1	1,6		1,6	4		1,6	4
	$D$4	x2	0		0	4		0	4
	$E$4	x3	0,8		0,8	4		0,8	4

14. Wyznaczamy drugie rozwiązanie optymalne:

• dla pierwszego warunku dodajemy do b₁ wartość dopuszczalnego wzrostu (z raportu wrażliwości); prawa strona pierwszego warunku ograniczającego = 4, dopuszczalny wzrost = 3, stąd obecna wartość prawej strony pierwszego warunku ograniczającego = 7;

• wracamy do danych z zadania 2, zmieniamy wyraz wolny b₁,w komórkę G6 wpisujemy 7, w komórki C4:E4 wpisujemy 0 i ustawiamy się w komórceF4 (komórki F4 i F6:F9 automatycznie się wyzerują);

• następnie ponownie rozwiązujemy zadanie za pomocą pakietu Solver (Narzędzia/Solver);

• rozwiązanie zadania:

Rozwiązanie I:

X1 = 1,6

X2 = 0

X3 = 0,8

FC = 2*X1 + 2*X2 + 1*X3 = 4

Rozwiązanie II

X1 = 1

X2 = 0

X3 = 2

FC = 2*X1 + 2*X2 + 1*X3 = 4

3. Problem rozkroju

Zad. 3.

Rozwiąż zadanie programowania liniowego całkowitoliczbowego - zad. 30 str. 44 Badania operacyjne w przykładach i zadaniach pod red. K. Kukuły, PWN: Warszawa 2001, stosując moduł Solver /Excel/.

W pewnym zakładzie produkcyjnym z arkusza blachy o standardowych wymiarach wycina się trzy rodzaje elementów: A, B i C. Można stosować pięć sposobów rozkroju jednego arkusza blachy. W poniższej tablicy podano liczby elementów uzyskanych przy zastosowaniu poszczególnych sposobów rozkroju oraz zużycie blachy na każdy element.

Elementy	Sposoby rozkroju 1 arkusza					Zużycie blachy na 1 element (w m^2)
	I	II	III	IV	V
A	1	1	0	0	0	0,7
B	1	0	2	1	0	0,4
C	0	4	2	5	8	1,1

Ile razy należy zastosować możliwe sposoby rozkroju, aby otrzymać nie więcej niż 800 elementów A, nie więcej niż 1 000 elementów B i co najmniej 800 elementów C, zużywając przy tym możliwie najmniej blachy.

Postać standardowa modelu:

Fc: 1,1X1 + 5,1X2 + 3X3 + 5,9X4 + 8,8X5 → MIN

Wo. X1 + X2 ≤ 800 (1.)

X1 + 2X3 + X4 ≤ 1 000 (2.)

4X2 + 2X3 + 5X4 + 8X5 ≥ 800 (3.)

Wb. Xi ≥ 0 Xi ∈ C

Moduł Solver /Excel/:

1. Korzystamy z modelu decyzyjnego w postaci standardowej.

2. Otwieramy nowy arkusz Excel-a, nazywamy go zad.3. Wprowadzamy dane w następujący sposób:

a/ współczynniki funkcji celu (wagi funkcji celu) w zakres: B3:F3,

b/ zmienne decyzyjne w zakres: B4:F4,

c/ wartości początkowe zmiennych decyzyjnych (dla każdej zmiennej wpisujemy wartość początkową 0) w zakres: B5:F5,

d/ współczynniki warunków ograniczających w zakres: B10:F12,

e/ wyrazy wolne warunków ograniczających w zakres: H10:H12,

f/ komórkę G5 przeznaczamy na wartość funkcji celu dla bieżących wartości zmiennych decyzyjnych. W komórce tej wprowadzamy funkcję Excel-a: =SUMA.ILOCZYNÓW(B3:F3;B5:F5),

g/ w komórkach G10:G12 zapisujemy formuły obliczania wartości lewych stron warunków ograniczających zadania optymalizacyjnego dla bieżących wartości zmiennych decyzyjnych według wzoru G10: =SUMA.ILOCZYNÓW(B10:F10;$B$5:$F$5); formułę z komórki G10 kopiujemy do komórek G11, G12.

3. Wybieramy z menu Narzędzia opcję Solver. Wyświetli się okno dialogowe Solver - Parametry.

4. W okno Komórka celu wprowadzamy adres komórki z formułą obliczania wartości funkcji celu ($G$5).

5. Wybieramy jedno z kryteriów optymalizacji - w naszym zadaniu będzie to Min.

6. W polu Komórki zmieniane wprowadzamy zakres komórek, w które wcześniej wpisaliśmy wartości zerowe zmiennych decyzyjnych ($B$5:$F$5).

7. W pole Warunki ograniczające za pomocą przycisku Dodaj wprowadzamy kolejne warunki ograniczające.

8. Otworzy się okno Dodaj warunek ograniczający. W polu Adres komórki wprowadzamy adres komórki zawierającej formułę obliczania wartości lewej strony pierwszego warunku ograniczającego ($G$10), następnie wybieramy symbol właściwej relacji (<=), a w polu Warunek ograniczający wprowadzamy adres komórki zawierającej wartość wyrazu wolnego pierwszego warunku ograniczającego ($H$10). W analogiczny sposób dodajemy kolejne warunki ograniczające.

9. 
   W zadaniach całoliczbowych dodatkowym warunkiem narzuconym przez charakter zmiennych jest aby wszystkie zmienne decyzyjne były liczbami całkowitymi, stąd ostatnim warunkiem jaki należy wprowadzić jest zapis:

10. Po wprowadzeniu ostatniego warunku ograniczającego klikamy OK i wracamy do okna Solver - Parametry.

11. Klikamy w oknie dialogowym w Opcje i zaznaczamy: Przyjmij model liniowy oraz Przyjmij nieujemne (warunek nieujemności zmiennych decyzyjnych - X_j ≥ 0), potwierdzamy OK.

12. W oknie Solver - Parametry klikamy przycisk Rozwiąż i otrzymujemy okno dialogowe, w którym zaznaczamy raport Wyników. UWAGA: w zadaniach optymalizacji całoliczbowej nie ustala się raportu wrażliwości i raportu granic.

13. Rozwiązanie zadania otrzymujemy zarówno w arkuszu, w którym wprowadzaliśmy dane jak i w Raporcie wyników.

Microsoft Excel 8.0a Raport wyników
Komórka celu (Min)
	Komórka	Nazwa	Wartość początkowa	Wartość końcowa
	$G$5		0	880
Komórki decyzyjne
	Komórka	Nazwa	Wartość początkowa	Wartość końcowa
	$B$5	X1	0	0
	$C$5	X2	0	0
	$D$5	X3	0	0
	$E$5	X4	0	0
	$F$5	X5	0	100

Warunki ograniczające
	Komórka	Nazwa	Wartość komórki	formuła	Status	Luz
	$G$10	[1]	0	$G$10<=$H$10	Nie wiążące	800
	$G$11	[2]	0	$G$11<=$H$11	Nie wiążące	1000
	$G$12	[3]	800	$G$12>=$H$12	Wiążące	0
	$B$5	X1	0	$B$5=całkowita	Wiążące	0
	$C$5	X2	0	$C$5=całkowita	Wiążące	0
	$D$5	X3	0	$D$5=całkowita	Wiążące	0
	$E$5	X4	0	$E$5=całkowita	Wiążące	0
	$F$5	X5	100	$F$5=całkowita	Wiążące	0

12. Przy postawionym warunku całoliczbowości niemożliwe jest sprawdzenie czy zadanie ma więcej rozwiązań. Usuwając to założenie uzyskamy raport wrażliwości (warunkiem jego wykorzystania jest otrzymanie po tej operacji rozwiązania w liczbach całkowitych).

15. Przypomnijmy że rozwiązanie nie jest jedynym rozwiązaniem optymalnym:

a/ jeżeli w raporcie wrażliwości wartość końcowa i przyrost krańcowy zmiennej decyzyjnej są równe zero lub jeżeli przynajmniej dla jednego warunku ograniczającego cena dualna jest równa zero i odpowiedni warunek ograniczający jest wiążący (w raporcie wyników).

W związku z tym, że dla rozwiązywanego zadania nie są spełnione wymienione warunki istnieje tylko jedno rozwiązanie optymalne.

Rozwiązanie: X 1 = 0, X2 = 0, X3 = 0, X4 = 0, X5 = 100, Fc. = 880

ANALIZA WRAŻLIWOŚCI ROZWIĄZANIA OPTYMALNEGO

Zad.1 str. 23. Badania operacyjne w przykładach i zadaniach pod red. K. Kukuły, PWN: Warszawa 2001.

Rozwiązanie - Excel - Solver

Kukuła 1
F.celu	1	3
Zmienne	X1	X2
wartości	4800	7000	25800
Warunki ograniczające
{1}	3	1	21400	33000	Prawe strony
{2}	1	1	11800	13000	warunków
{3}	5	8	80000	80000	ograniczających
{4}	0	1	7000	7000

Okno dialogowe Solver - Wyniki pozwala na generowanie trzech raportów: raportu wyników, raportu wrażliwości i raportu granic dla decyzji optymalnej.

W raporcie wyników z zawartości części pierwszej Komórka celu wynika, że maksymalny, przy danych warunkach ograniczających zysk ze sprzedaży wyrobów wyniesie 25800.

Osiągnięcie takiego wyniku jest możliwe (por. część druga Komórki decyzyjne) dzięki wyprodukowaniu 4800 sztuk wyrobu pierwszego i 7000 sztuk wyrobu drugiego. Widzimy, że Solver rozpoczynał obliczenia zwiększając wartości zmiennych decyzyjnych od 0 i taka była początkowo wartość funkcji celu.

Z ostatniego - trzeciego fragmentu raportu wyników (Warunki ograniczające) dowiadujemy się, że ograniczenia opisujące pracę obrabiarek O1 i O2 są luźne (nie wiążące) przy decyzji optymalnej, natomiast warunki dotyczące pracy frezarki F oraz wielkości produkcji wyrobu drugiego są napięte (wiążące) przy decyzji optymalnej. Oznacza to, że przy optymalnym planie produkcji w pełni zostaną wykorzystane moce produkcyjne frezarki (ograniczenie typu <= i dlatego luz dla trzeciego warunku równy jest 0) i wypełniony plan produkcji wyrobu drugiego - maksymalny popyt = 7000 (ograniczenie typu <= i stąd luz dla czwartego warunku równy jest 0). Wartość 11600 w kolumnie Luz dla pierwszego warunku ograniczającego informuje, że po wykonaniu optymalnego planu produkcji niewykorzystane jest 11600 godzin pracy obrabiarki O1, analogicznie wartość 1200 w kolumnie Luz dla warunku drugiego wskazuje, że po wykonaniu optymalnego planu produkcji niewykorzystane jest 1200 godzin obrabiarki O2.

Microsoft Excel 9.0 Raport wyników
1. Komórka celu (Maks)
	Komórka	Nazwa	Wartość początkowa	Wartość końcowa
	$D$6	wartości	0	25800
2. Komórki decyzyjne
	Komórka	Nazwa	Wartość początkowa	Wartość końcowa
	$B$6	wartości x1	0	4800
	$C$6	wartości x2	0	7000
3. Warunki ograniczające
	Komórka	Nazwa	Wartość komórki	formuła	Status	Luz
	$D$9	{1}	21400	$D$9<=$E$9	Nie wiążące	11600
	$D$10	{2}	11800	$D$10<=$E$10	Nie wiążące	1200
	$D$11	{3}	80000	$D$11<=$E$11	Wiążące	0
	$D$12	{4}	7000	$D$12<=$E$12	Wiążące	0

Raport wrażliwości Solvera składa się z dwóch części. Pierwsza część (komórki decyzyjne) zawiera następujące informacje:

• dla obu zmiennych decyzyjnych (X1 i X2) wartość w kolumnie Przyrost krańcowy jest równa zero, co oznacza, że jakakolwiek zmiana dodatnich wartości zmiennych decyzyjnych nie może być brana pod uwagę. Dodatkowo uzyskujemy informację, że w tym przykładzie, wyznaczona przez Solver decyzja optymalna stanowi jedyne rozwiązanie optymalne analizowanego modelu decyzyjnego (por. ćw. 1-2 i 3 punkt 13 oraz wiadomości dot. budowy tablicy simpleksowej),

• liczby w kolumnach Dopuszczalny wzrost i Dopuszczalny spadek określają tzw. zakresy stabilności decyzji optymalnej względem zmian wartości poszczególnych wag funkcji celu. I tak, z wiersza przyporządkowanego zmiennej X1 odczytujemy, że jeśli współczynnik c₁ z funkcji celu (zysk jednostkowy wyrobu pierwszego równy 1 zł) zmniejszy się nie więcej niż o 1 zł, czyli w tym przypadku obniży się do (niemal) zera, to nie spowoduje to zmiany decyzji optymalnej przy niezmienionym zysku jednostkowym wyrobu drugiego wynoszącym c₂ = 3 zł). Zmiana decyzji nie nastąpi również, gdy c₁ wzrośnie nie więcej niż 0,875 zł za sztukę (niezmienną decyzję optymalną otrzymamy jeśli c_i ∈ (0, 1,875>. Zmieni się jednak wartość funkcji celu. Analogiczne informacje dotyczące produkcji wyrobu drugiego zawiera wiersz raportu przyporządkowany zmiennej X2. Dowiadujemy się zatem, że nawet spadek wartości c₂ - zysku jednostkowego osiąganego ze sprzedaży wyrobu drugiego o 1,4 zł (tj. do wysokości 1,6 zł) nie spowoduje zmiany decyzji optymalnej. Decyzji optymalnej nie zmieni również wzrost c₂ - zysku ze sprzedaży wyrobu drugiego - o dowolną wartość dodatnią (symbolicznie określoną jako 10³⁰), co faktycznie oznacza brak ograniczenia z góry, a zatem niezmienioną decyzję optymalną uzyskamy jeżeli wartość c₂ ∈ <1,6; +∞).

Microsoft Excel 9.0 Raport wrażliwości
1. Komórki decyzyjne
			Wartość	Przyrost	Współczynnik	Dopuszczalny	Dopuszczalny
	Komórka	Nazwa	końcowa	krańcowy	funkcji celu	wzrost	spadek
	$B$6	wartości x1	4800	0	1	0,875	1
	$C$6	wartości x2	7000	0	3	1E+30	1,4

Druga część raportu wrażliwości dotyczy warunków ograniczających i zawiera informacje o stabilności decyzji optymalnej względem zmian wyrazów wolnych z warunków ograniczających:

• w kolumnie wartość końcowa podawane są ponownie wartości lewych stron warunków ograniczających, uzyskane przy optymalnych wartościach zmiennych decyzyjnych. Stąd identyczna wartość kolumny wartość komórki w raporcie wyników (w raporcie wyników dane z kolumny wartość komórki służyły za podstawę do podziału warunków na wiążące (napięte) i niewiążące (luźne). W raporcie wrażliwości dowiadujemy się o możliwości innej interpretacji bilansu wartości lewej i prawej strony każdego z warunków przy uzyskanej decyzji optymalnej. Interpretacja ta związana jest z tzw. cenami dualnymi wyrazów wolnych b_i.

Pierwszy i drugi warunek ograniczający w analizowanym zadaniu są niewiążące (luźne):

a/ luźny pierwszy warunek ograniczający przy decyzji optymalnej oznacza, że limit czasu pracy obrabiarki pierwszej (O1) nie został wykorzystany w całości (b₁ = 21400), należy stwierdzić, że wydłużenie czasu pracy tej obrabiarki powyżej 21400 nie wpłynie na wzrost produkcji , a co za tym idzie również na wielkość zysku - wskazuje na to zerowa wartość ceny dualnej pierwszego wyrazu wolnego,

b/ drugi warunek ograniczający jest także niewiążący przy decyzji optymalnej, co oznacza, że limit czasu pracy obrabiarki drugiej (O2) nie został wykorzystany w całości (b₂ = 11800), należy stwierdzić, że wydłużenie czasu pracy tej obrabiarki powyżej 11800 nie wpłynie na wzrost produkcji i na wielkość zysku - wskazuje na to zerowa wartość ceny dualnej drugiego wyrazu wolnego

Trzeci i czwarty warunek ograniczający są napięte (wiążące) przy decyzji optymalnej. Oznacza to, że:

a/ dostępny czas pracy frezarki jest wykorzystany w całości. Gdyby jednak była możliwość zwiększenia czasu pracy tej maszyny o godzinę, przy niezmienionym czasie pracy innych urządzeń, to wówczas optymalny plan produkcji wyrobów nr 1 i 2 gwarantowałby łączny zysk o 0,2 zł większy od maksymalnego zysku 25800 zł osiąganego bez zwiększania czasu pracy tego urządzenia,

b/ wielkość produkcji wyrobu drugiego uwarunkowana jest popytem (warunek 4), a warunek ten dla decyzji optymalnej jest wiążący, co oznacza, że produkowana jest największa możliwa do przyjęcia przez rynek ilość tego wyrobu. Gdyby jednak uwarunkowania rynkowe zmieniły się (przy niezmienionych innych ograniczeniach), to ewentualne powiększenie produkcji tego wyrobu o sztukę (7001) spowodowałoby wzrost zysku z produkcji o 1,4 zł. tj. do kwoty 25801,4.

2. Warunki ograniczające
			Wartość	Cena	Prawa strona	Dopuszczalny	Dopuszczalny
	Komórka	Nazwa	końcowa	dualna	w. o.	wzrost	spadek
	$D$9	{1}	21400	0	33000	1E+30	11600
	$D$10	{2}	11800	0	13000	1E+30	1200
	$D$11	{3}	80000	0,2	80000	6000	24000
	$D$12	{4}	7000	1,4	7000	3000	2000

Informacje zawarte w komórkach Dopuszczalny wzrost i Dopuszczalny spadek drugiej części raportu wrażliwości dotyczą zmian wyrazów wolnych, ale takich zmian, które nie zmienią zestawu dodatnich zmiennych w decyzji optymalnej, chociaż wartości tych zmiennych mogą ulegać zmianie. Zmiany poszczególnych prawych stron warunków ograniczających można rozpatrywać zakładając stałość pozostałych (tzn. inne wyrazy wolne są ustalone jak w zadaniu wyjściowym):

a/ jeśli limit czasu pracy obrabiarki O1 zmniejszyłby się o co najwyżej 11600 godzin (do dolnej granicy krytycznej 21400) lub zwiększyłby się o dowolną wielkość (górna granica 10³⁰) nie spowodowałoby to żadnych zmian w wielkości produkcji obu wyrobów (warunek [1] jest luźny),

b/ podobnie, jeśli limit czasu pracy obrabiarki O2 zmniejszyłby się o co najwyżej 1200 godzin (do dolnej granicy krytycznej 11800) lub zwiększyłby się o dowolną wielkość (górna granica 10³⁰) nie spowodowałoby to żadnych zmian w wielkości produkcji obu wyrobów (warunek [2] jest luźny),

c/ w przypadku gdy limit czasu pracy frezarki F zmniejszy się co najwyżej o 24000 godzin (do dolnej wartości krytycznej 56000) albo zwiększy się co najwyżej o 6000 godzin (do górnej wartości krytycznej wynoszącej 86000 godzin) optymalny plan produkcji będzie nadal przewidywał produkcję obu rodzajów wyrobów (wartość funkcji celu zmieni się o b₃^` * 0,2 zł). Łączny zysk zmieniałby się od 21000 do 27000 zł przy niezmienionych pozostałych wyrazach wolnych,

d/ jeżeli limitowana wielkość produkcji wyrobu drugiego zmniejszy się o co najwyżej 2000 sztuk (do dolnej wartości krytycznej 5000) albo zwiększy się o nie więcej niż 3000 sztuk (do górnej wartości krytycznej wynoszącej 10000 sztuk) optymalny plan produkcji będzie nadal przewidywał produkcję obu rodzajów wyrobów (wartość funkcji celu zmieni się o b₄` * 1,4 zł), a zatem łączny zysk zmieniałby się od 23000 do 30000 zł przy pozostałych warunkach ograniczających nie zmienionych.

Ostatni z prezentowanych w Solverze raportów - raport granic - podaje informacje o dopuszczalnych zakresach zmian wartości każdej ze zmiennych decyzyjnych, które osiągnęły wartość dodatnią, przy niezmienionych wartościach pozostałych zmiennych decyzyjnych. Trzeba tu wskazać, że każda taka zmiana musi spowodować zmianę - pogorszenie - wartości funkcji celu. Z raportu granic dla analizowanego zadania wynika, że gdyby wartość zmiennej decyzyjnej X1 - wielkość produkcji wyrobu pierwszego - wynosiła zero, to przy niezmienionej wartości drugiej ze zmiennych decyzyjnych funkcja celu wyniosłaby 21000 zł, natomiast gdyby wartość zmiennej decyzyjnej X2 - wielkość produkcji wyrobu drugiego - wynosiła zero, to przy niezmienionej wartości pierwszej zmiennej decyzyjnej funkcja celu wynosiłaby 4800 zł

Microsoft Excel 9.0 Raport granic
		Cel
	Komórka	Nazwa	końcowa
	$D$6	wartości	25800
		Zmienne decyzyjne		Dolna	Cel	Górna	Cel
	Komórka	Nazwa	końcowa	granica	Wynik	granica	Wynik
	$B$6	wartości x1	4800	0	21000	4800	25800
	$C$6	wartości x2	7000	0	4800	6999,999859	25799,99958

Badania operacyjne - Zastosowanie metody simplex do rozwiązywania zadań programowania liniowego. Zagadnienie 1: wybór struktury asortymentowej produkcji.

Rozwiąż zadanie programowania liniowego - zad.1 str. 23 Badania operacyjne w przykładach i zadaniach pod red. K. Kukuły, PWN: Warszawa 2001. Wykorzystaj program Badania operacyjne z komputerem (programowanie liniowe).

Program Badania operacyjne z komputerem (programowanie liniowe)

1. Otwieramy katalog Bad_oper, uruchamiamy program Bad_op (w celu uzyskania „dużego ekranu” klikamy w znajdujący się u góry ekranu znak *).

2. Wybieramy opcję Programowanie liniowe.

3. W opcji Wybór funkcji wybieramy Wprowadzenie nowego zadania.

4. Wprowadzenie zadania polega na ustaleniu:

• rodzaju zadania: MAKSYMALIZACJA,

• liczby zmiennych: 2 ,

• liczby ograniczeń: 4,

• wag funkcji celu,

• współczynników stojących przy zmiennych decyzyjnych w warunkach ograniczających,

• wprowadzenie rodzaju ograniczeń: ≤,

• wyrazów wolnych warunków ograniczających.

UWAGA:

5. Wprowadzamy nazwę pliku: KUKULA 1.

6. Powrót do opcji Wybór funkcji i wybór wariantu Rozwiązanie zadania.

7. Sprowadzenie zadania do postaci bazowej (jest to postać kanoniczna).

• wybieramy ograniczenia (Wybór ograniczenia) oraz dodajemy zmienne bilansujące (Dodaj zmienną bilansującą). Uwaga: zmiennymi bilansującymi nazwano w tym programie zmienne swobodne,

• po uzupełnieniu wszystkich warunków ograniczających zmiennymi bilansującymi wybieramy opcję Koniec operacji.

8. Otrzymujemy pierwszą tablicę simpleksową (Pierwsza iteracja).

9. Algorytm dalszego postępowanie przedstawia schemat.

10. Pełne zestawienie wyników kolejnych etapów rozwiązania zadania PL przedstawiono poniżej.

Badania operacyjne -Zastosowanie metody simpleks ze sztuczną bazą do rozwiązywania zadań programowania liniowego. Zagadnienie 2: Problem mieszanki.

Rozwiąż zadanie programowania liniowego POKEMON. Wykorzystaj program Badania operacyjne z komputerem (programowanie liniowe).

Program Badania operacyjne z komputerem (programowanie liniowe)

1. Otwieramy katalog Bad_oper, uruchamiamy program Bad_op.

2. Wybieramy opcję Programowanie liniowe.

3. W opcji Wybór funkcji wybieramy Wprowadzenie nowego zadania.

4. Wprowadzenie zadania polega na ustaleniu:

• rodzaju zadania: MINIMALIZACJA,

• liczby zmiennych: 3 ,

• liczby ograniczeń: 3,

• wag funkcji celu,

• współczynników stojących przy zmiennych decyzyjnych w warunkach ograniczających,

• wprowadzenie rodzaju ograniczeń (≥, =, ≤),

• wyrazów wolnych warunków ograniczających.

UWAGA:

• Przy wprowadzaniu danych nie używamy przecinków („ ,”) tylko kropki („ .”).

• Każdą operację potwierdzamy wybierając ENTER.

• Znaki używane w programie BAD_OPER wprowadzamy z klawiatury: = ograniczenie typu „=”, < ograniczenie typu „≤”, > ograniczenie typu „≥”

5. Wprowadzamy nazwę pliku: POKEMON

6. Powrót do opcji Wybór funkcji i wybór wariantu Rozwiązanie zadania.

7. Sprowadzenie zadania do postaci bazowej (jest to postać kanoniczna).

• wybieramy ograniczenia (Wybór ograniczenia) oraz: w warunku pierwszym odejmujemy zmienną bilansującą i dodajemy zmienną sztuczną, w warunku drugim dodajemy zmienną sztuczną, w warunku trzecim dodajemy zmienną bilansującą,

• po uzupełnieniu wszystkich warunków ograniczających zmiennymi bilansującymi i sztucznymi wybieramy opcję Koniec operacji.

8. Otrzymujemy pierwszą tablicę simpleksową (Pierwsza iteracja).

9. Algorytm dalszego postępowanie przedstawia schemat.

10. Pełne zestawienie wyników kolejnych etapów rozwiązania zadania PL przedstawiono poniżej.

Badania operacyjne - Zastosowanie metody simplex do rozwiązywania zadań programowania liniowego. Zagadnienie 3: Problem rozkroju.

Rozwiąż zadanie programowania liniowego całkowitoliczbowego - zad. 30 str. 44 Badania operacyjne w przykładach i zadaniach pod red. K. Kukuły, PWN: Warszawa 2001. Zastosuj: Program Badania operacyjne z komputerem (programowanie całoliczbowe).

Program Badania operacyjne z komputerem (programowanie całoliczbowe)

1. Otwieramy katalog Bad_oper, uruchamiamy program Bad_op.

2. Wybieramy opcję Programowanie całoliczbowe.

3. W opcji Wybór funkcji wybieramy Wprowadzenie nowego zadania.

4. Wprowadzenie zadania polega na ustaleniu:

• rodzaju zadania: MINIMALIZACJA,

• liczby zmiennych: 5 ,

• liczby ograniczeń: 3,

• wag funkcji celu,

• współczynników stojących przy zmiennych decyzyjnych w warunkach ograniczających,

• typów ograniczeń (≤, ≤, ≥)

• wyrazów wolnych warunków ograniczających.

UWAGA:

• Przy wprowadzaniu danych nie używamy przecinków („ ,”) tylko kropki („ .”).

• Każdą operację potwierdzamy wybierając ENTER.

• Znaki używane w programie BAD_OPER wprowadzamy z klawiatury: = ograniczenie typu „=”, < ograniczenie typu „≤”, > ograniczenie typu „≥”

5. Wprowadzamy nazwę pliku: KUKULA 30.

6. Powrót do opcji Wybór funkcji i wybór wariantu Rozwiązanie zadania.

7. Sprowadzenie zadania do postaci bazowej (jest to postać kanoniczna).

• wybieramy ograniczenia (Wybór ograniczenia) oraz w warunkach pierwszym i drugim dodajemy zmienne bilansujące (Dodaj zmienną bilansującą), w warunku trzecim odejmujemy zmienną bilansującą i dodajemy zmienną sztuczną. Uwaga: zmiennymi bilansującymi nazwano w tym programie zmienne swobodne,

• po uzupełnieniu wszystkich warunków ograniczających wybieramy opcję Koniec operacji.

8. Otrzymujemy pierwszą tablicę simpleksową (Pierwsza iteracja).

9. Algorytm dalszego postępowania przedstawia schemat.

10. Pełne zestawienie wyników kolejnych etapów rozwiązania zadania PL przedstawiono poniżej.

1

Wyrazy wolne warunków ograniczających

Wartości lewych stron warunków ograniczających

Wartość funkcji celu

Współczynniki warunków ograniczających

Wartości początkowe zmiennych decyzyjnych

Zmienne decyzyjne

Wagi funkcji celu

UWAGA:

• Przy wprowadzaniu danych nie używamy przecinków („ ,”) tylko kropki („ .”).

• Każdą operację potwierdzamy klawiszem ENTER

• Znaki używane w programie BAD_OPER wprowadzamy z klawiatury: = ograniczenie typu „=”, < ograniczenie typu „≤”, > ograniczenie typu „≥”

.

Kryterium simpleksowe

Lewe strony warunków ograniczających

Funkcja celu

Zmienna decyzyjna

Waga funkcji celu

---