Akademia Górniczo Hutnicza

im. Stanisław Staszica

Wydział Inżynierii Mechanicznej i Robotyki

Wytrzymałość materiałów - projekt 1a

Temat:

Obliczanie głównych, centralnych momentów bezwładności przekroju symetrycznego i niesymetrycznego

(zadanie 20)

Wykonał:

Temat 1:

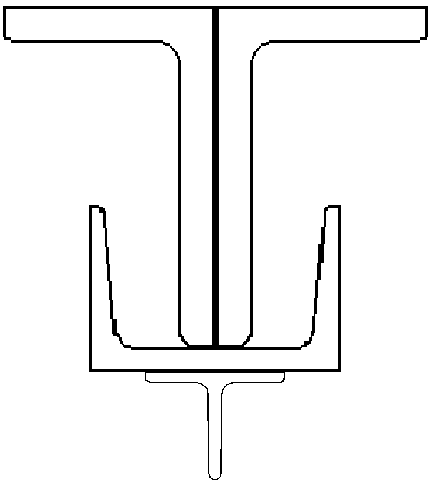
Obliczyć główne centralne momenty bezwładności dla przekroju przedstawionego na rysunku:

1. Dane obliczeniowe:

A­₁

11 [cm­²]

e

1,45 [cm]

I_x1

106 [cm⁴]

I_y1

19,4 [cm⁴]

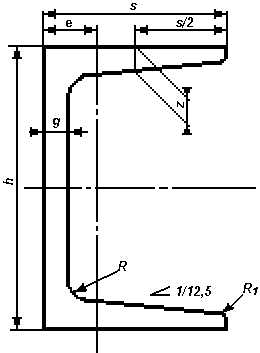
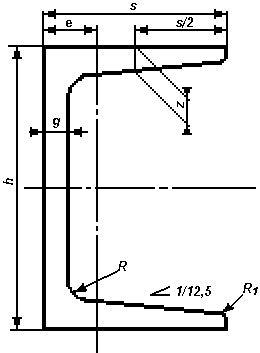
1.1 Charakterystyka geometryczna ceownika C80 wg normy PN 86/H-93403 symbol wielkość h 8 [cm] s 4,5 [cm] g 0,6 [cm]
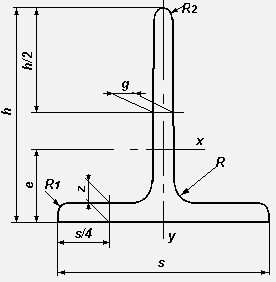
1.2 Charakterystyka geometryczna teownika T 30x30 wg PN-91/H-93406 symbol wielkość h 3 [cm] s 3 [cm] g 0,4 [cm] A­1 2,3 [cm­^2] e 0,85 [cm] Ix1 1,72 [cm^4] Iy1 0,87 [cm^4]

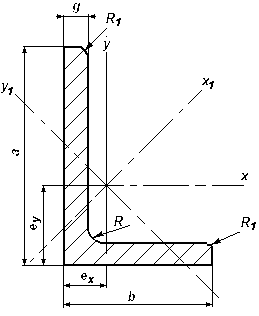
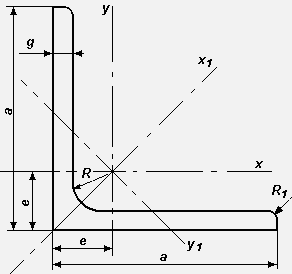
1.1 Charakterystyka geometryczna kątownika nierównoramiennego L 70x50x7 wg normy PN-81/H-93402 symbol wielkość a 7 [cm] b 5 [cm] g 0,7 [cm] A­1 7,95 [cm­^2] ex 2,28 [cm] ey 1,29 [cm] Ix1 38,3 [cm^4] Iy1 16,2 [cm^4]

2. Obliczenie środka ciężkości profili względem przyjętych osi y_c,x₁

2.1 Obliczanie odległości środków ciężkości profili walcowych od osi y_c, x₁

Profil	Ceownik C80			Teownik T30x30
Symbol	xc1	yc1	A1	xc2	yc2	A2
Wzór	-	ec	-	-	-et	-
Wartość	0[cm]	1,45 [cm]	11 [cm­^2]	0[cm]	-0,85 [cm]	2,3 [cm­^2]

Profil	Kątownik L 70x50x7 (lewy)			Kątownik L 70x50x7 (prawy)
Symbol	xc3	yc3	A3	xc4	yc4	A4
Wzór	-eky	gc+ak- ekx	-	eky	gc+ak- ekx	-
Wartość	-1,29 [cm]	0,6+7-2,28 =5,32[cm]	7,95 [cm­^2]	1,29 [cm]	0,6+7-2,28 =5,32[cm]	7,95 [cm­^2]

2.2 Obliczenie środka ciężkości

x_c=0 [cm] ponieważ oś y_c pokrywa się z osią symetrii przekroju

y_c=S_x/A_c

A_c=11+2,3+2*7,95=29,2 [cm²]

y_c=(11*1,45+2,3*-0,85+2*7,95*5,32)/29,2=3,38

3. Obliczanie centralnych momentów bezwładności i dewiacji względem osi y_c, x_c umieszczonych w środku ciężkości profilu.

3.1 Obliczanie odległości środków ciężkości profili walcowych od osi y_c, x_c

Profil	Ceownik C80		Teownik T30x30		Kątownik L 70x50x7 (lewy)		Kątownik L 70x50x7 (prawy)
Symbol	x01	y01	x02	y02	x03	y03	x04	y04
Wzór	-	-yc+ec	-	-yc+et	-eky	yc4- yc	eky	yc4- yc
Wartość	0[cm]	-3,38+1,45 =-1,93 [cm]	0[cm]	-3,38-0,85 =-4,23[cm]	-1,29 [cm]	1,94 [cm]	1,29 [cm]	1,94 [cm]

3.2 Obliczanie momentów bezwładności względem osi y_c, x_c dla całkowitego przekroju z wykorzystanie wzorów Steinera.

I_x0=I_x1+ I_x2+ I_x3+ I_x4=I_xC80+A_C80*y₀₁²+ I_xT30+A_t30*y₀₂²+2* (I_xK+A_K*y₀₃²)=

=19,4+11*-1,93²+1,72+2,3*-4,32²+2*(38,3+7,95*1,94²)=241,46 [cm⁴]

I_y0=I_y1+ I_y2+ I_y3+ I_y4=I_yC80+A_C80*x₀₁²+ I_yT30+A_t30*x₀₂²+2*(I_yK+A_K*x₀₃²)=

=106+0,87+2*(16,2+7,95*1,29²)=165,73 [cm⁴]

Temat 2:

Obliczyć główne centralne momenty bezwładności dla przekroju niesymetrycznego:

1. Dane obliczeniowe:

1.1 Charakterystyka geometryczna ceownika C80 wg normy PN 86/H-93403 symbol wielkość h 24 [cm] s 8,5 [cm] g 0,95 [cm] A­1 42,3 [cm­^2] e 2,23 [cm] Ix1 3600 [cm^4] Iy1 248 [cm^4]
1.2 Charakterystyka geometryczna kątownika równoramiennego L 75x75x10 wg PN-91/H-93407 symbol wielkość a 7,5 [cm] g 1 [cm] A­1 14,1 [cm­^2] e 2,22 [cm] Ix1= Iy1 72,2 [cm^4]

2. Obliczenie środka ciężkości profilu względem przyjętych osi y₁,x₁. Układ współrzędnych został umieszczony w środku ciężkości ceownika.

2.1 Obliczanie odległości środków ciężkości profili walcowych od osi y₁, x₁

Profil	Ceownik C240			Kątownik równoramienny
Symbol	x1	y1	A1	x2	y2	A2
Wzór	-	-	-	sc-ec+ak- ek	-hc/2+ek	-
Wartość	0[cm]	0 [cm]	42,3 [cm­^2]	11,55 [cm]	-9,78 [cm]	14,1 [cm­^2]

2.2 Obliczenie środka ciężkości

A_c=42,3+14,1=56,4 [cm­²]

x_c=S_y­/A_c=(14,1*11,55)/56,4=2,89[cm]

y_c=S_x­/A_c=(14,1*-9,78)/56,4=-2,45[cm]

3. Obliczanie centralnych momentów bezwładności i dewiacji względem osi umieszczonych w środku ciężkości profilu.

3.1 Obliczanie odległości środków ciężkości profili walcowych od osi y_g, x_g przechodzących przez środek ciężkości.

Profil	Ceownik C240		Kątownik równoramienny
Symbol	x01	y01	x02	y02
Wzór	xc	yc	x2- xc	y2- yc
Wartość	2,89 [cm]	-2,45 [cm]	11,55-2,89=8,66[cm]	-9,78+2,45=-7,33[cm]

3.2 Obliczanie centralnych momentów bezwładności oraz momentu dewiacji względem osi dla całkowitego przekroju z wykorzystanie wzorów Steinera.

I_xc= I_xcc+ I_xck= I_xcc+ A₁* y₀₁²+I_xck+ A₂* y₀₂²=3600+42,3*-2,45²+72,2+14,1*-7,33²= 4689,09[cm⁴]

I_yc= I_ycc+ I_yck= I_ycc+ A₁* x₀₁²+I_yck+ A₂* x₀₂²=248+42,3*2,89²+72,2+14,1*8,66²=1730,93 [cm⁴]

I_xcyc= A₁* y₀₁* x₀₁²+ A₂* y₀₂* x₀₂²=42,3*2,89*-2,45+14,1*8,66*-7,33= -1194,54 [cm⁴]

4. Obliczanie wartości głównych momentów bezwładności oraz kąta o jaki należy obrócić układ współrzędnych, by stał się on układem głównym.

I_min,max=I_xg,yg­= (I_xc+ I_yc)/2±

I₀=
=>

=> I₁=1308,8[cm⁴], I₂=5111,22[cm⁴]

tg2α=-2*
/(
)=-2*-1194,54/(
)=0,807624

2α=arcrg(0,807624)=38,93°

α=19,46°

1

---