Przykład projektowania łuku poziomego nr 1 z symetrycznymi klotoidami,
łuku poziomego nr 2 z niesymetrycznymi klotoidami i krzywej esowej łączącej oba łuki
Politechnika Białostocka - ZID
- 1 -
mgr inż. Marek Motylewicz
1.
Dane
Droga klasy technicznej G 1/2 , Vp = 60 km/h poza terenem zabudowanym
Prędkość miarodajna: Vm = 90 km/h (Vm = 100 km/h dla krętości trasy = 53,40 °/km
i dla drogi o szerokości jezdni 7,0 m bez utwardzonych poboczy –
zredukowano do wartości Vm = 90 km/h z uwagi na zapis w §13
pkt. 2 Dz.U.99.43.430)
Pomiar trasy:
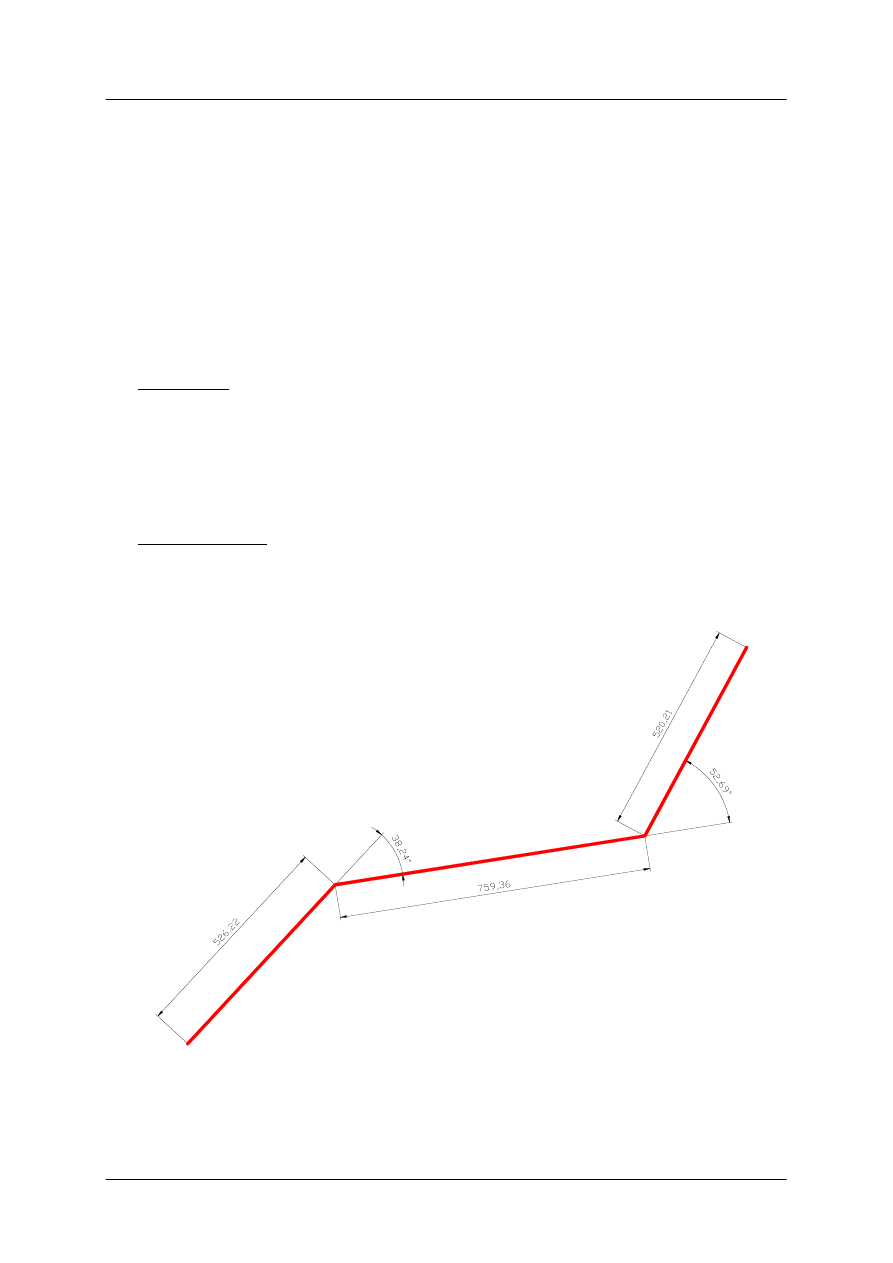
|AB| = 526,22 m
|BC| = 759,36 m
|CD| = 520,21 m
Kąty zwrotu trasy:
γ
1
= 38,24 °
γ
2
= 52,69 °
B
C
D
A
Rys. 1.
Przykład projektowania łuku poziomego nr 1 z symetrycznymi klotoidami,
łuku poziomego nr 2 z niesymetrycznymi klotoidami i krzywej esowej łączącej oba łuki
Politechnika Białostocka - ZID
- 2 -
mgr inż. Marek Motylewicz
2.
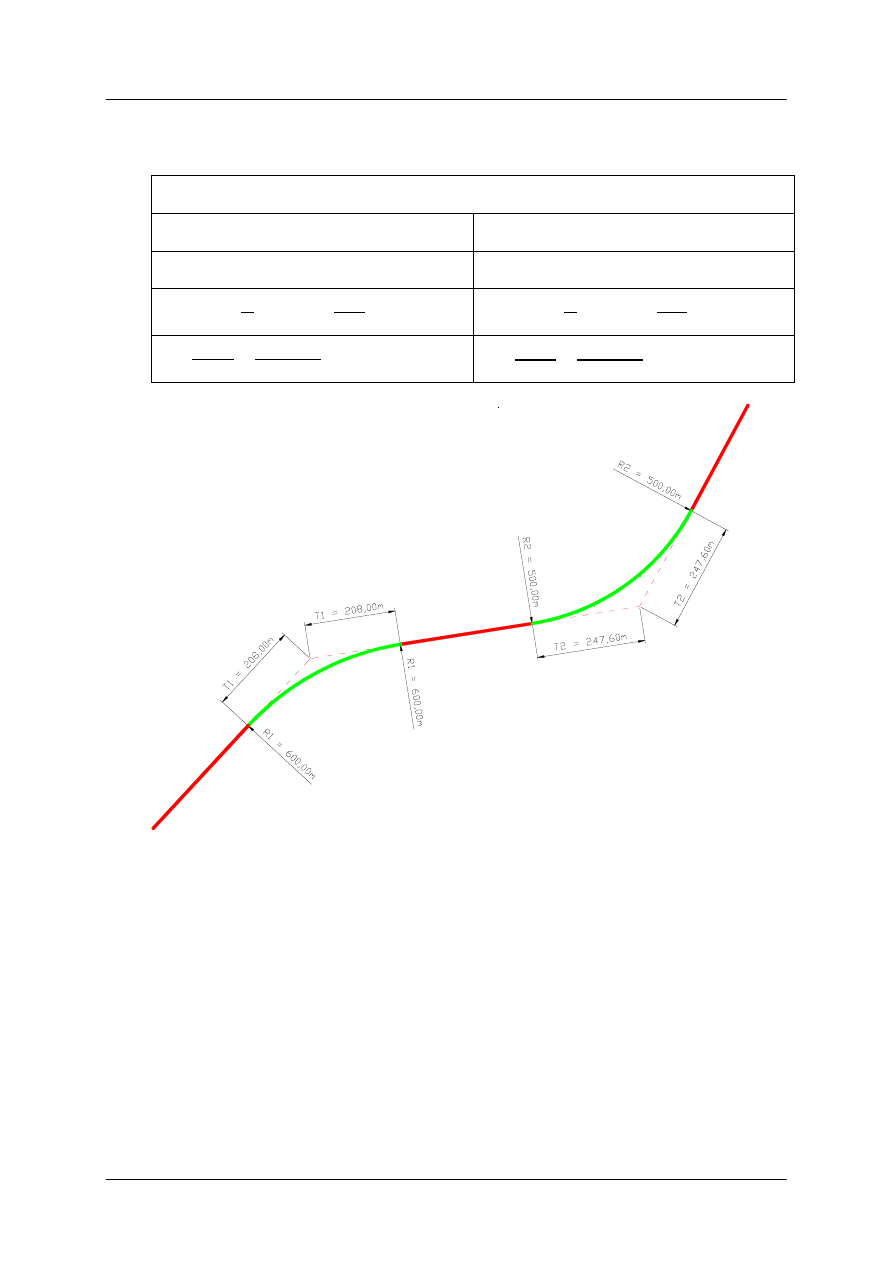
Zaprojektowano dwa łuki poziome o następujących danych
R
min
= 200,00 m (i = 7%)
R
1
= 600,00 m
R
2
= 500,00 m
i
1
= 5%
i
2
= 6%
T
1
=
·
భ
600 ·
,
= 208,00 m
T
2
=
·
మ
500 ·
,
= 247,60 m
Ł
1
=
·
భ
·
భ
°
··,
°
= 400,45 m
Ł
2
=
·
మ
·
మ
°
··,
°
= 459,81 m
C
A
D
B
Rys. 2.
3.
Zestawienie długości trasy (przed wpisaniem krzywych przejściowych)
PPT = 0,00 m
km 7+200,00
PŁK
1
= |AB| – T
1
= 526,22 – 208,00 = 318,22 m
km 7+518,22
SŁK
1
= PŁK
1
+ 0,5 · Ł
1
= 318,22 + 0,5 · 400,45 = 518,45 m
km 7+718,45
KŁK
1
= PŁK
1
+ Ł
1
= 318,22 + 400,45 = 718,67 m
km 7+918,67
PŁK
2
= KŁK
1
+ (|BC| – T
1
– T
2
) = 718,67 + (759,36 – 208,00 – 247,60 m) = 1022,43 m
km 8+222,43
SŁK
2
= PŁK
2
+ 0,5 · Ł
2
= 1022,43 + 0,5 · 459,81 = 1252,34 m
km 8+452,34
KŁK
2
= PŁK
2
+ Ł
2
= 1022,43 + 459,81 = 1482,24 m
km 8+682,24
KPT = KŁK
2
+ (|CD| – T
2
) = 1482,24 + (520,21 – 247,60) = 1754,85 m
km 8+954,85
Przykład projektowania łuku poziomego nr 1 z symetrycznymi klotoidami,
łuku poziomego nr 2 z niesymetrycznymi klotoidami i krzywej esowej łączącej oba łuki
Politechnika Białostocka - ZID
- 3 -
mgr inż. Marek Motylewicz
4.
Projektowanie układu klotoid symetrycznych nr 1a i 1b dla łuku poziomego nr 1
4.1.
Ustalenie parametru A
1
•
warunek dynamiki: „Klotoida powinna być na tyle duża, aby przyrost
przyspieszenia nie następował zbyt szybko.”
a
V
A
3
p
1
w
∆
≥
gdzie:
V
p
- prędkość projektowa, V
p
= 70 km/h =
19,44 m/s
;
∆
a - przyrost przyspieszenia dośrodkowego,
dla V
p
= 70 km/h wg Dz.U. nr 43 poz. 430 odczytano
∆
a = 0,6 m/s
3
.
stąd obliczono:
65
,
110
6
,
0
44
,
19
A
3
1
w
=
≥
•
warunek geometrii: „Suma katów zwrotu obu klotoid łuku nie może być większa od
kąta zwrotu trasy, gdyż nie byłaby zachowana geometryczna ciągłość łuku. Gdy
suma katów klotoid równa jest kątowi zwrotu trasy, klotoidy stykają się (brak
części łukowej) tworząc krzywą zwaną biklotoidą.”
γ
⋅
≤
R
A
2
w
R
1
= 600 m;
γ
1
= 38,24º = 0,6674 rad
stąd obliczono:
17
,
490
6674
,
0
600
A
2
w
=
⋅
≤
•
warunek estetyki: „
Warunek został ustalony na podstawie oceny istniejących odcinków
dróg. Stwierdzono, że klotoidy o kątach zwrotu od 3° do 30°
dają najlepszą optyczną
płynność trasy.
”
R
A
R
3
1
3
w
≤
≤
stąd obliczono:
00
,
600
A
00
,
200
3
w
≤
≤
Przykład projektowania łuku poziomego nr 1 z symetrycznymi klotoidami,
łuku poziomego nr 2 z niesymetrycznymi klotoidami i krzywej esowej łączącej oba łuki
Politechnika Białostocka - ZID
- 4 -
mgr inż. Marek Motylewicz
•
warunek minimalnego odsunięcia od stycznej: „
Odsunięcie łuku kołowego powinno
być zauważalne dla kierowcy.
”
4
min
3
4
w
H
R
24
A
⋅
⋅
≥
H
min
= 0,5 m (dopuszczalne 0,2 m)
przyjęto: H
min
= 0,5 m
stąd obliczono:
64
,
225
5
,
0
600
24
A
4
3
4
w
=
⋅
⋅
≥
•
warunek proporcji krzywych: „
Ze względu na płynność trasy między długością klotoid a
długością łuku kołowego powinna zachodzić odpowiednia proporcja.
”
1
n
R
Ł
A
1
n
R
Ł
5
w
+
⋅
≤
≤
+
⋅
gdzie: n
zalecane
= 1 do 2, n
dopuszczalne
= 0,5 do 4
przyjęto: n = 1 ÷ 2
stąd obliczono:
1
1
600
45
,
400
A
1
2
600
45
,
400
5
w
+
⋅
≤
≤
+
⋅
60
,
346
A
00
,
283
5
w
≤
≤
Tabela 4.1. Zestawienie obliczonych przedziałów wartości parametru A
1
110,65 ≤
A
w1
A
w2
≤
490,17
200,00 ≤
A
w3
≤
600,00
225,64 ≤
A
w4
283,00 ≤
A
w5
≤ 346,60
•
Analizując wszystkie powyższe obliczenia przyjęto wartość parametru
A
1
= 300,00 m
Przykład projektowania łuku poziomego nr 1 z symetrycznymi klotoidami,
łuku poziomego nr 2 z niesymetrycznymi klotoidami i krzywej esowej łączącej oba łuki
Politechnika Białostocka - ZID
- 5 -
mgr inż. Marek Motylewicz
4.2.
Dla obliczonego parametru A
1
odczytano z tablic wartości elementów klotoidy
jednostkowej i przeliczono je na wartości rzeczywiste
•
Ustalenie parametru wejściowego do tablic
ଵ
ଵ
ଵ
300
600
0,500
•
Odczytanie z tablic Lipińskiego wartości elementów klotoidy jednostkowej nr 1
i obliczenie wartości rzeczywistych
Tabela 4.2. Wartości klotoidy jednostkowej i obliczenie wartości rzeczywistych
Wartości klotoidy
jednostkowej
Wartości rzeczywiste szukanej klotoidy
(wielkości
liniowe
x A
1
)
τ
1
= 7º 09’ 43’’
τ
1
= 7,1619º
(przeliczone na wartość dziesiętną)
x
1
= 0,499219
X
1
= 149,7657 m
y
1
= 0,020810
Y
1
= 6,2430 m
x
s1
= 0,249870
X
s1
= 74,9610 m
h
1
= 0,005206
H
1
= 1,5618 m
l
1
= 0,500000
L
1
= 150,0000 m
(długość zaprojektowanej klotoidy)
4.3.
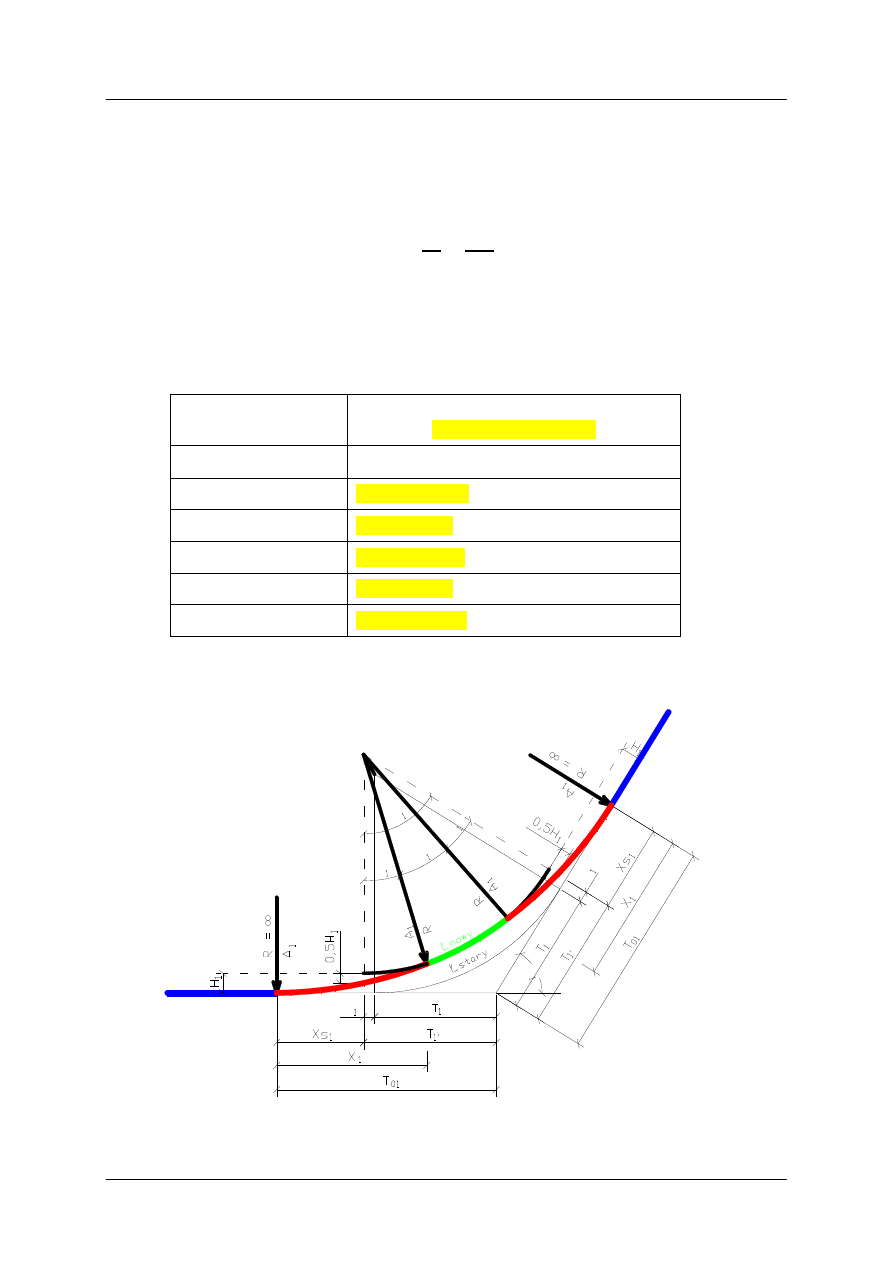
Kreślenie układu klotoid symetrycznych nr 1a i 1b dla łuku poziomego nr 1
∆
τ
α
τ
γ
γ
∆
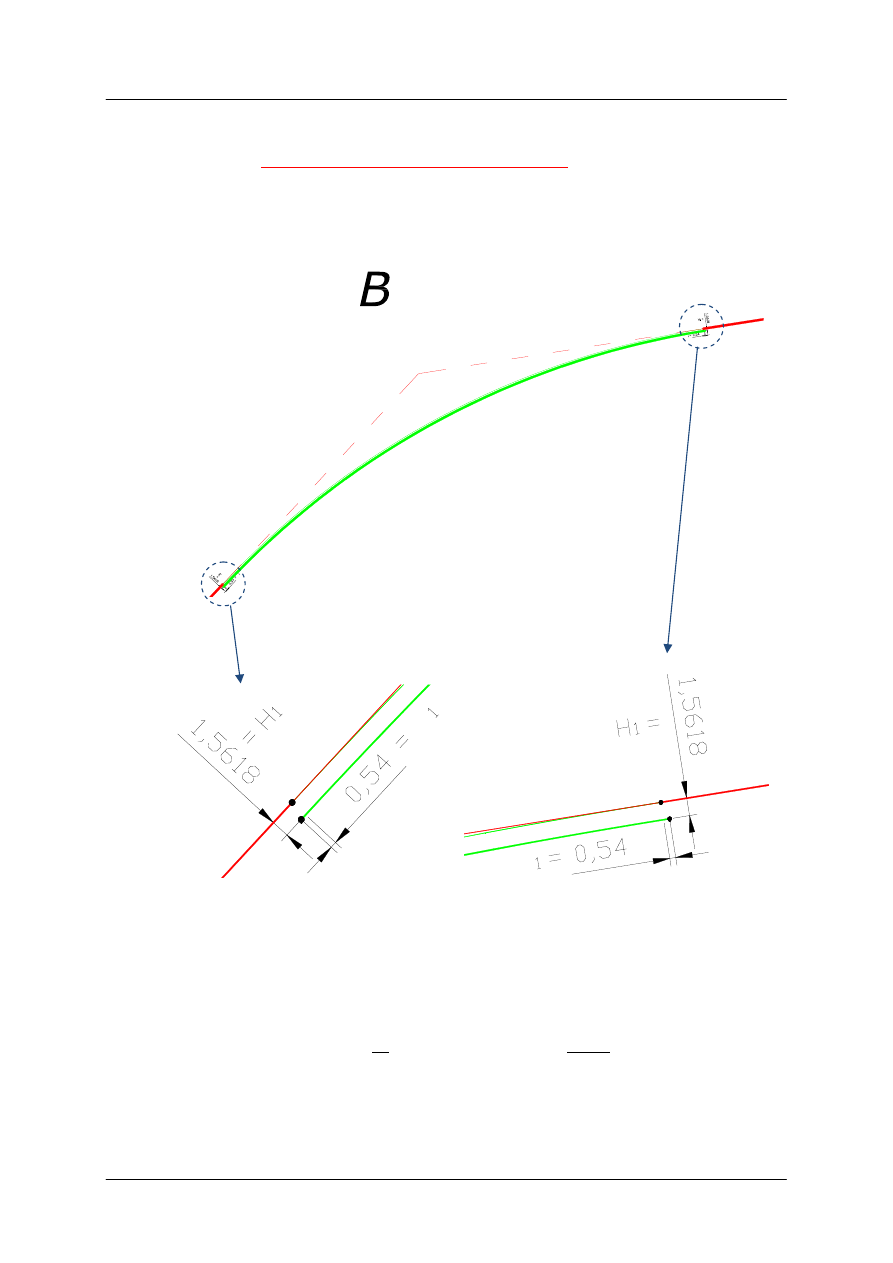
Rys. 3. Przypadek łuku poziomego z symetrycznymi klotoidami
Przykład projektowania łuku poziomego nr 1 z symetrycznymi klotoidami,
łuku poziomego nr 2 z niesymetrycznymi klotoidami i krzywej esowej łączącej oba łuki
Politechnika Białostocka - ZID
- 6 -
mgr inż. Marek Motylewicz
4.3.1.
Przesuwamy łuk kołowy o wartość H
1
prostopadle od obu stycznych trasy (łuk po
przesunięciu
musi mieć tą samą wartość promienia!!!
)
H
1
= 1,5618 m (prostopadle od obu stycznych)
∆
∆
∆
∆
Rys. 4.
4.3.2.
Obliczamy wartość nowej stycznej T
1’
(wg rys. 3)
ଵᇱ
ଵ
ଵ
·
ଵ
2
600 1,5618 ·
38,24
2
208,54
4.3.3.
Obliczamy wartość przesunięcia poziomego
∆∆∆∆
1111
∆
ଵ
ଵᇱ
ଵ
208,54 208,00 0,54
Przykład projektowania łuku poziomego nr 1 z symetrycznymi klotoidami,
łuku poziomego nr 2 z niesymetrycznymi klotoidami i krzywej esowej łączącej oba łuki
Politechnika Białostocka - ZID
- 7 -
mgr inż. Marek Motylewicz
4.3.4.
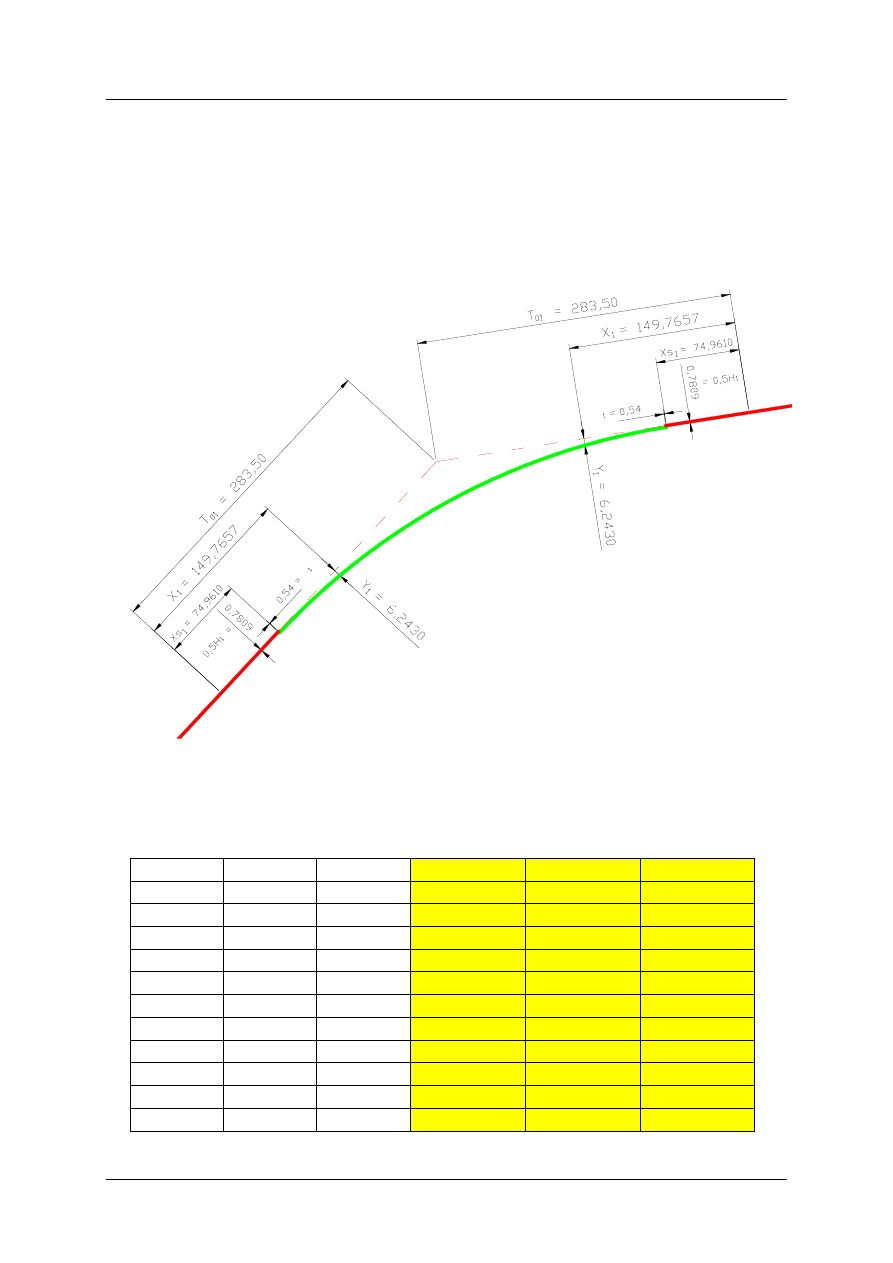
Odmierzamy na rysunku wartości X
s1
oraz 0,5·H
1
; X
1
oraz Y
1
(z tabeli nr 4.2)
W ten sposób wyznaczamy trzy główne punkty projektowanej klotoidy:
−
początek (PKP) – wyznacza go początek X
s1
−
ś
rodek (SKP) – wyznacza go odcięta X
s1
oraz rzędna 0,5·H
1
−
koniec (KKP) – wyznacza go odcięta X
1
oraz rzędna Y
1
∆
∆
B
P
K
P
1
b
S
K
P
1
b
K
Ł
K
/
K
K
P
1
b
PK
P
1
a
S
K
P
1
a
K
K
P
1
a
/
PŁ
K
Rys. 5.
4.3.5.
Odczytujemy z tablic punkty pośrednie (zakładając krok wartości „l”) i tyczymy
kolejne punkty klotoidy metodą rzędnych i odciętych od PKP (z obu stron)
l
x
y
L [m] = l · A
X [m] = x · A
Y [m] = y · A
0,050
0,050000
0,000021
15,0000
15,0000
0,0063
0,100
0,100000
0,000167
30,0000
30,0000
0,0501
0,150
0,149998
0,000562
45,0000
44,9994
0,1686
0,200
0,199992
0,001333
60,0000
59,9976
0,3999
-
-
-
-
74,9610 = Xs
0,7809 = 0,5H
0,250
0,249976
0,002604
75,0000
74,9928
0,7812
0,300
0,299939
0,004499
90,0000
89,9817
1,3497
0,350
0,349869
0,007144
105,0000
104,9607
2,1432
0,400
0,399744
0,010662
120,0000
119,9232
3,1986
0,450
0,449539
0,015176
135,0000
134,8617
4,5528
0,500
0,499219
0,020810
150,0000 = L
149,7657 = X
6,2430 = Y
Przykład projektowania łuku poziomego nr 1 z symetrycznymi klotoidami,
łuku poziomego nr 2 z niesymetrycznymi klotoidami i krzywej esowej łączącej oba łuki
Politechnika Białostocka - ZID
- 8 -
mgr inż. Marek Motylewicz
S
K
P
1
a
K
K
P
1
a
/ P
ŁK
PK
P
1
a
X [m]
Y [m]
1.
15,0000
0,0063
2.
30,0000
0,0501
3.
44,9994
0,1686
4.
59,9976
0,3999
5.
74,9610 = Xs
1
0,7809 = 0,5H
1
6.
74,9928
0,7812
7.
89,9817
1,3497
8.
104,9607
2,1432
9.
119,9232
3,1986
10.
134,8617
4,5528
11.
149,7657 = X
1
6,2430 = Y
1
Rys. 6.
Po obustronnym wpisaniu krzywych (odbicie lustrzane – symetria) otrzymujemy rozwiązanie
zadania – układ klotoid symetrycznych nr 1a i 1b dla łuku poziomego nr 1 (rys. 7)
P
K
P
1
b
S
K
P
1
b
K
Ł
K
/
K
K
P
1
b
B
P K
P
1
a
K
K
P
1
a
/ P
Ł K
S
K
P
1
a
Rys. 7.
Przykład projektowania łuku poziomego nr 1 z symetrycznymi klotoidami,
łuku poziomego nr 2 z niesymetrycznymi klotoidami i krzywej esowej łączącej oba łuki
Politechnika Białostocka - ZID
- 9 -
mgr inż. Marek Motylewicz
Na potrzeby wpisania krzywej esowej możemy jednak pominąć
wpisywanie krzywej nr 1b pozostawiając odsunięty łuk nr 1 (rys. 8)
S
K
P
1
a
K
K
P
1
a
/ P
Ł K
P K
P
1
a
B
Rys. 8.
4.3.6.
Obliczamy długość klotoid nr 1a i 1b (z podstawowego wzoru klotoidy)
L
ଵ
A
ଵ
ଶ
R
ଵ
300
ଶ
600
150,00 m
4.3.7.
Obliczamy styczną T
01
układu krzywa przejściowa – łuk poziomy (wg rys. 3)
ଵ
ଵᇱ
௦ଵ
ଵ
∆
ଵ
௦ଵ
208,54 74,9610 283,50
Przykład projektowania łuku poziomego nr 1 z symetrycznymi klotoidami,
łuku poziomego nr 2 z niesymetrycznymi klotoidami i krzywej esowej łączącej oba łuki
Politechnika Białostocka - ZID
- 10 -
mgr inż. Marek Motylewicz
5.
Projektowanie układu klotoid niesymetrycznych nr 2 i 3 dla łuku poziomego nr 2
5.1.
Ustalenie parametru A
2
i A
3
•
warunek dynamiki: „Klotoida powinna być na tyle duża, aby przyrost
przyspieszenia nie następował zbyt szybko.”
a
V
A
3
p
1
w
∆
≥
gdzie:
V
p
- prędkość projektowa, V
p
= 70 km/h =
19,44 m/s
;
∆
a - przyrost przyspieszenia dośrodkowego,
dla V
p
= 70 km/h wg Dz.U. nr 43 poz. 430 odczytano
∆
a = 0,6 m/s
3
.
stąd obliczono:
65
,
110
6
,
0
44
,
19
A
3
1
w
=
≥
•
warunek geometrii: „Suma katów zwrotu obu klotoid łuku nie może być większa od
kąta zwrotu trasy, gdyż nie byłaby zachowana geometryczna ciągłość łuku. Gdy
suma katów klotoid równa jest kątowi zwrotu trasy, klotoidy stykają się (brak
części łukowej) tworząc krzywą zwaną biklotoidą.”
γ
⋅
≤
R
A
2
w
R
2
= 500 m;
γ
2
= 52,69º = 0,9196 rad
stąd obliczono:
48
,
479
9196
,
0
500
A
2
w
=
⋅
≤
•
warunek estetyki: „
Warunek został ustalony na podstawie oceny istniejących odcinków
dróg. Stwierdzono, że klotoidy o kątach zwrotu od 3° do 30°
dają najlepszą optyczną
płynność trasy.
”
R
A
R
3
1
3
w
≤
≤
stąd obliczono:
00
,
500
A
67
,
166
3
w
≤
≤
Przykład projektowania łuku poziomego nr 1 z symetrycznymi klotoidami,
łuku poziomego nr 2 z niesymetrycznymi klotoidami i krzywej esowej łączącej oba łuki
Politechnika Białostocka - ZID
- 11 -
mgr inż. Marek Motylewicz
•
warunek minimalnego odsunięcia od stycznej: „
Odsunięcie łuku kołowego powinno
być zauważalne dla kierowcy.
”
4
min
3
4
w
H
R
24
A
⋅
⋅
≥
H
min
= 0,5 m (dopuszczalne 0,2 m)
przyjęto: H
min
= 0,5 m
stąd obliczono:
80
,
196
5
,
0
500
24
A
4
3
4
w
=
⋅
⋅
≥
•
warunek proporcji krzywych: „
Ze względu na płynność trasy między długością klotoid a
długością łuku kołowego powinna zachodzić odpowiednia proporcja.
”
1
n
R
Ł
A
1
n
R
Ł
5
w
+
⋅
≤
≤
+
⋅
gdzie: n
zalecane
= 1 do 2, n
dopuszczalne
= 0,5 do 4
przyjęto: n = 1 ÷ 2
stąd obliczono:
1
1
500
81
,
459
A
1
2
500
81
,
459
5
w
+
⋅
≤
≤
+
⋅
05
,
339
A
83
,
276
5
w
≤
≤
Tabela 5.1. Zestawienie obliczonych przedziałów wartości parametru A
2
i A
3
110,65 ≤
A
w1
A
w2
≤
479,48
166,67 ≤
A
w3
≤
500,00
196,80 ≤
A
w4
276,83 ≤
A
w5
≤ 339,05
•
Analizując wszystkie powyższe obliczenia przyjęto wartość parametru
A
2
= 290,00 m
dla klotoidy nr 2 i wartość parametru
A
3
= 325,00 m dla klotoidy nr 3.
Przykład projektowania łuku poziomego nr 1 z symetrycznymi klotoidami,
łuku poziomego nr 2 z niesymetrycznymi klotoidami i krzywej esowej łączącej oba łuki
Politechnika Białostocka - ZID
- 12 -
mgr inż. Marek Motylewicz
5.2.
Dla obliczonych parametrów A
2
i A
3
odczytano z tablic wartości elementów klotoid
jednostkowych i przeliczono je na wartości rzeczywiste
•
Ustalenie parametru wejściowego do tablic
ଶ
ଶ
ଶ
290
500
0,580
ଷ
ଷ
ଶ
325
500
0,650
•
Odczytanie z tablic Lipińskiego wartości elementów klotoidy jednostkowej nr 2
i obliczenie wartości rzeczywistych
Tabela 5.2. Wartości klotoidy jednostkowej nr 2 i obliczenie wartości rzeczywistych
Wartości klotoidy
jednostkowej
Wartości rzeczywiste szukanej klotoidy
(wielkości
liniowe
x A
2
)
τ
2
= 9º 38’ 14’’
τ
2
= 9,6372º
(przeliczone na wartość dziesiętną)
x
2
= 0,578361
X
2
= 167,7247 m
y
2
= 0,032453
Y
2
= 9,4114 m
x
s2
= 0,289727
X
s2
= 84,0208 m
h
2
= 0,008122
H
2
= 2,3554 m
l
2
= 0,580000
L
2
= 168,2000 m
(długość zaprojektowanej klotoidy)
•
Odczytanie z tablic Lipińskiego wartości elementów klotoidy jednostkowej nr 3
i obliczenie wartości rzeczywistych
Tabela 5.3. Wartości klotoidy jednostkowej nr 3 i obliczenie wartości rzeczywistych
Wartości klotoidy
jednostkowej
Wartości rzeczywiste szukanej klotoidy
(wielkości
liniowe
x A
3
)
τ
3
= 12º 06’ 13’’
τ
3
= 12,1036º
(przeliczone na wartość dziesiętną)
x
3
= 0,647105
X
3
= 210,3091 m
y
3
= 0,045625
Y
3
= 14,8281 m
x
s3
= 0,324517
X
s3
= 105,4680 m
h
3
= 0,011424
H
3
= 3,7128 m
l
3
= 0,650000
L
3
= 211,2500 m
(długość zaprojektowanej klotoidy)
Przykład projektowania łuku poziomego nr 1 z symetrycznymi klotoidami,
łuku poziomego nr 2 z niesymetrycznymi klotoidami i krzywej esowej łączącej oba łuki
Politechnika Białostocka - ZID
- 13 -
mgr inż. Marek Motylewicz
5.3.
Kreślenie układu klotoid niesymetrycznych nr 2 i 3 dla łuku poziomego nr 2
∆
∆
τ
α
τ
γ
γ
UWAGA:
Wartości T
s2’
oraz T
s3’
mogą być mniejsze od T
2
(ujemne delty)
w zależności od kąta zwrotu
γ
oraz wartości przesunięć łuku H
2
i H
3
Rys. 9. Przypadek łuku poziomego z niesymetrycznymi klotoidami
5.3.1.
Przesuwamy łuk kołowy o wartość H
2
i H
3
prostopadle od obu stycznych trasy
(łuk po przesunięciu
musi mieć tą samą wartość promienia!!!
)
H
2
= 2,3554 m
;
H
3
= 3,7128 m
∆
∆
C
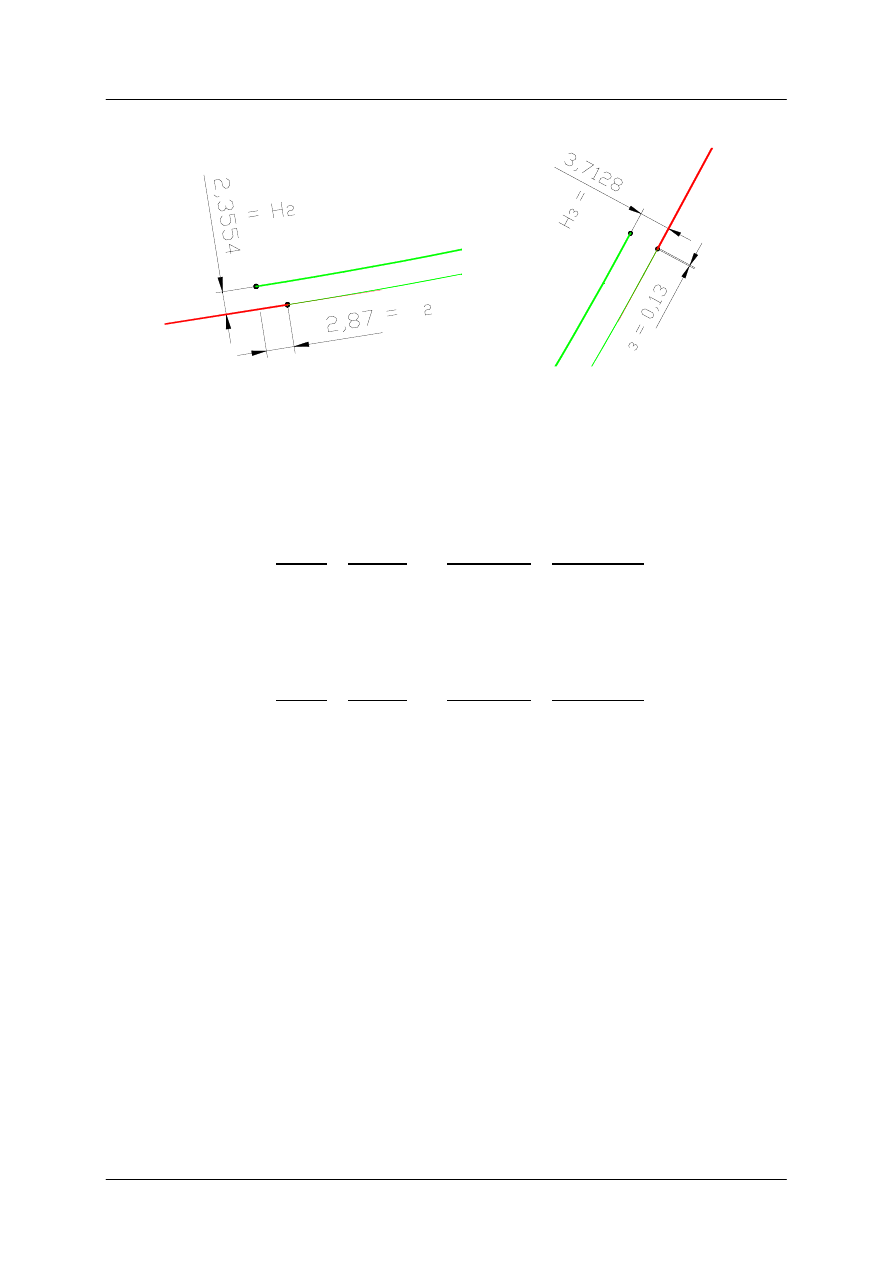
Przykład projektowania łuku poziomego nr 1 z symetrycznymi klotoidami,
łuku poziomego nr 2 z niesymetrycznymi klotoidami i krzywej esowej łączącej oba łuki
Politechnika Białostocka - ZID
- 14 -
mgr inż. Marek Motylewicz
∆
∆
Rys. 10.
5.3.2.
Obliczamy wartości stycznych T
s2’
oraz T
s3’
oraz wartości przesunięcia
poziomego
∆∆∆∆
2
i
∆
∆
∆
∆
3
(wg rys. 9)
௦ଶᇱ
ଶ
∆
ଶ
∆
ଶ
ଶ
ଶ
ଷ
sin
ଶ
2,3554
52,69°
3,7128
sin 52,69°
,
௦ଶᇱ
ଶ
∆
ଶ
247,60 2,87 250,47
௦ଷᇱ
ଶ
∆
ଷ
∆
ଷ
ଷ
ଶ
ଶ
sin
ଶ
3,7128
52,69°
2,3554
sin 52,69°
!, "#
௦ଷᇱ
ଶ
∆
ଷ
247,60 0,13 247,73
5.3.3.
Odmierzamy na rysunku wartości T
s2’
oraz X
s2
; 0,5·H
2
; X
2
oraz Y
2
(z tabeli 5.2)
oraz wartości T
s3’
oraz X
s3
; 0,5·H
3
; X
3
oraz Y
3
(z tabeli 5.3)
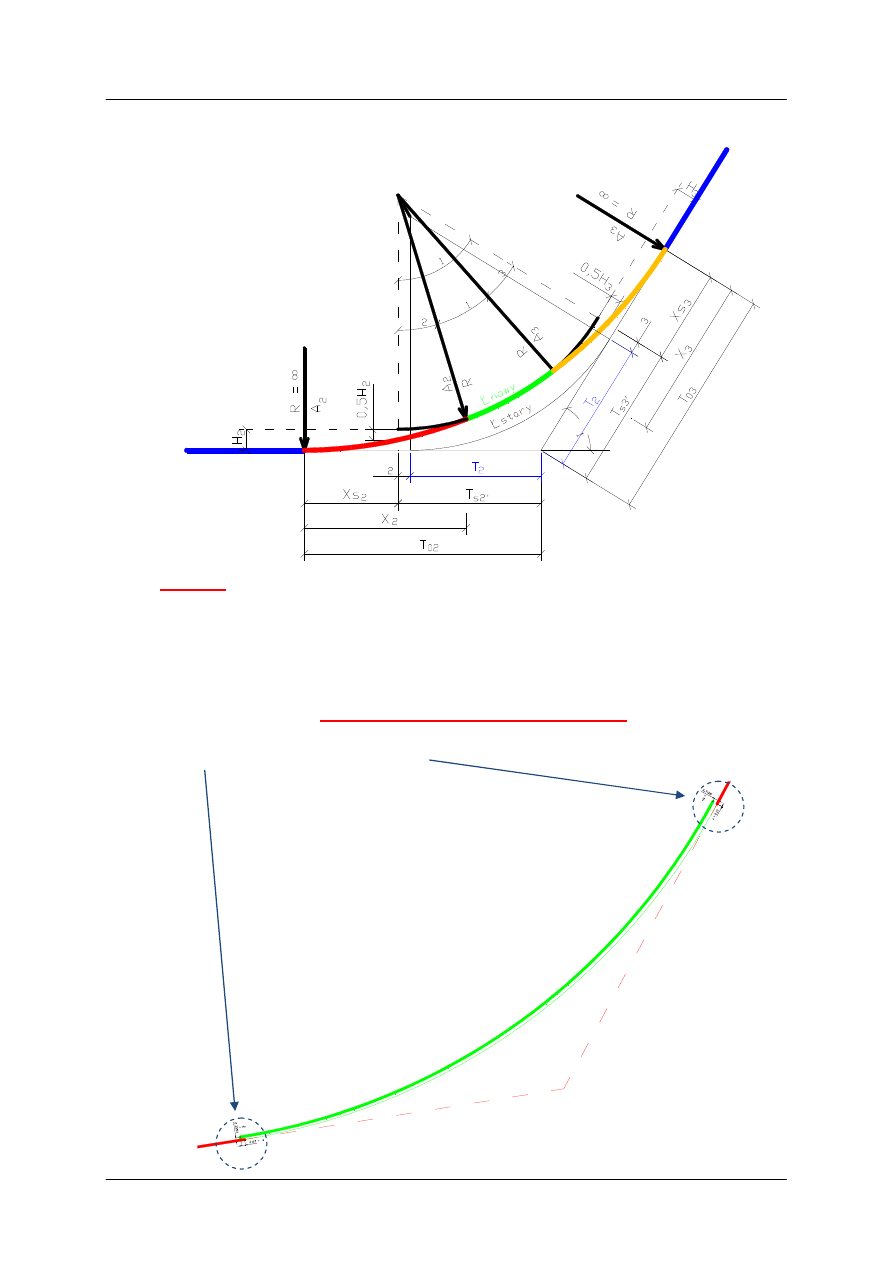
W ten sposób wyznaczamy trzy główne punkty projektowanej klotoidy:
−
początek (PKP) – wyznacza go początek X
s
−
ś
rodek (SKP) – wyznacza go odcięta X
s
(T
s’
) oraz rzędna 0,5·H
−
koniec (KKP) – wyznacza go odcięta X oraz rzędna Y
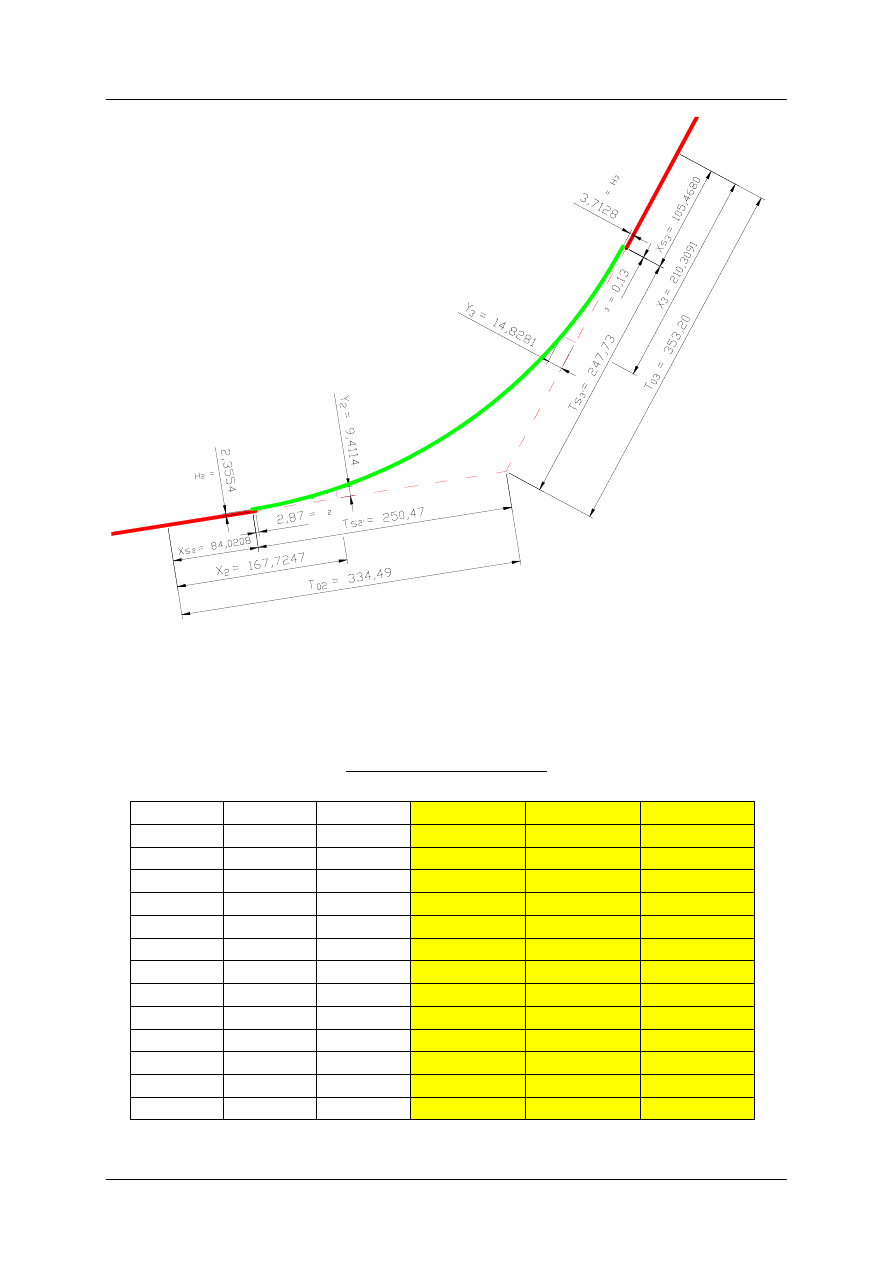
Przykład projektowania łuku poziomego nr 1 z symetrycznymi klotoidami,
łuku poziomego nr 2 z niesymetrycznymi klotoidami i krzywej esowej łączącej oba łuki
Politechnika Białostocka - ZID
- 15 -
mgr inż. Marek Motylewicz
KŁ K
2
/ P
KP
3
PK
P
3
SK
P
3
K
K
P
2
/
P
Ł
K
2
S
K
P
2
P
K
P
2
C
∆
∆
Rys. 11.
5.3.4.
Odczytujemy z tablic punkty pośrednie (zakładając krok wartości „l”) i tyczymy
kolejne punkty obu klotoid metodą rzędnych i odciętych od PKP
klotoida nr 2, A = 290,00 m
l
x
y
L [m] = l · A
X [m] = x · A
Y [m] = y · A
0,050
0,050000
0,000021
14,5000
14,5000
0,0061
0,100
0,100000
0,000167
29,0000
29,0000
0,0484
0,150
0,149998
0,000562
43,5000
43,4994
0,1630
0,200
0,199992
0,001333
58,0000
57,9977
0,3866
0,250
0,249976
0,002604
72,5000
72,4930
0,7552
-
-
-
-
84,0208 = Xs
1,1777 = 0,5H
0,300
0,299939
0,004499
87,0000
86,9823
1,3047
0,350
0,349869
0,007144
101,5000
101,4620
2,0718
0,400
0,399744
0,010662
116,0000
115,9258
3,0920
0,450
0,449539
0,015176
130,5000
130,3663
4,4010
0,500
0,499219
0,020810
145,0000
144,7735
6,0349
0,550
0,548743
0,027684
159,5000
159,1355
8,0284
0,580
0,578361
0,032453
168,2000 = L
167,7247 = X
9,4114 = Y
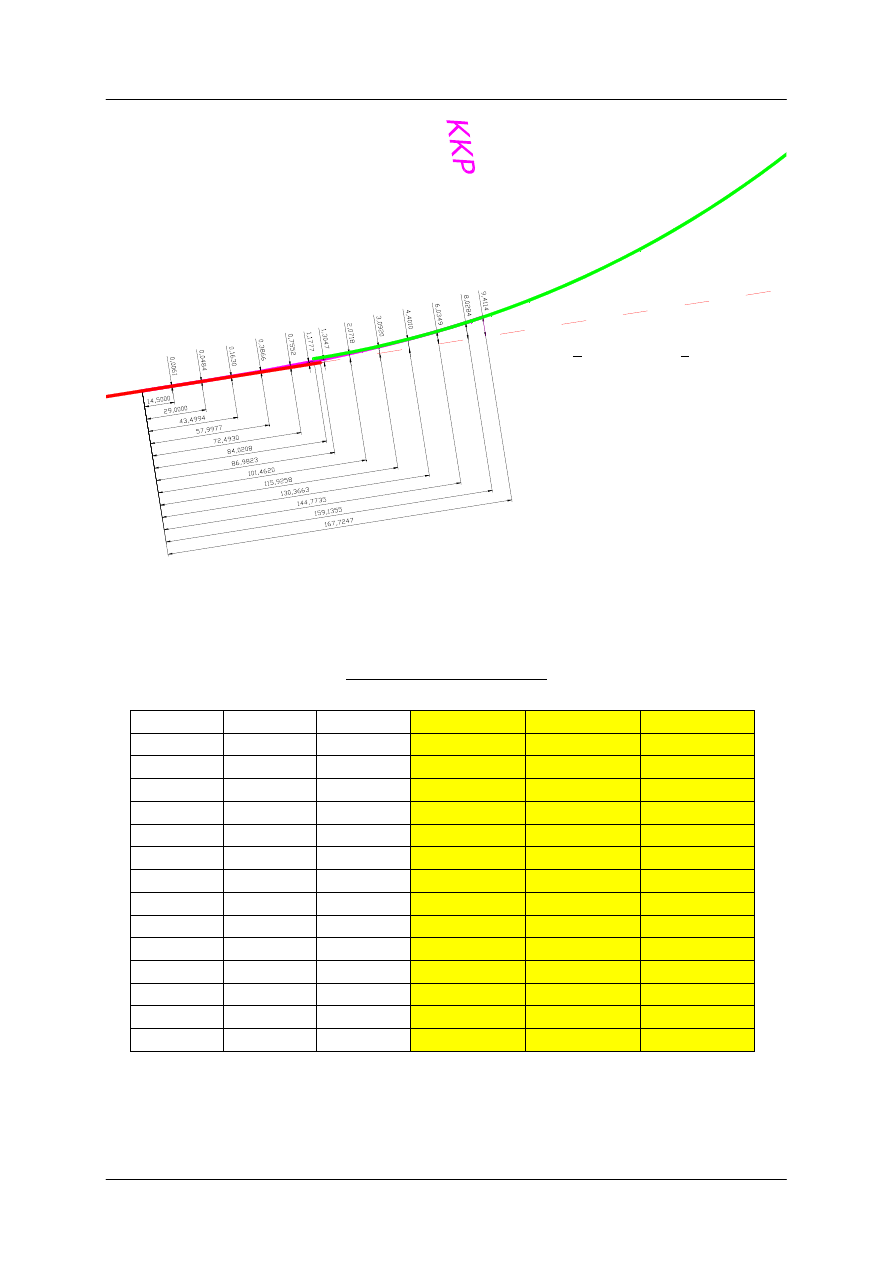
Przykład projektowania łuku poziomego nr 1 z symetrycznymi klotoidami,
łuku poziomego nr 2 z niesymetrycznymi klotoidami i krzywej esowej łączącej oba łuki
Politechnika Białostocka - ZID
- 16 -
mgr inż. Marek Motylewicz
P
K
P
2
S
K
P
2
2
/
P
Ł
K
2
X [m]
Y [m]
1.
14,5000
0,0061
2.
29,0000
0,0484
3.
43,4994
0,1630
4.
57,9977
0,3866
5.
72,4930
0,7552
6.
84,0208 = Xs
2
1,1777 = 0,5H
2
7.
86,9823
1,3047
8.
101,4620
2,0718
9.
115,9258
3,0920
10.
130,3663
4,4010
11.
144,7735
6,0349
12.
159,1355
8,0284
13.
167,7247 = X
2
9,4114 = Y
2
Rys. 12.
klotoida nr 3, A = 325,00 m
l
x
y
L [m] = l · A
X [m] = x · A
Y [m] = y · A
0,050
0,050000
0,000021
16,2500
16,2500
0,0068
0,100
0,100000
0,000167
32,5000
32,5000
0,0543
0,150
0,149998
0,000562
48,7500
48,7494
0,1827
0,200
0,199992
0,001333
65,0000
64,9974
0,4332
0,250
0,249976
0,002604
81,2500
81,2422
0,8463
0,300
0,299939
0,004499
97,5000
97,4802
1,4622
-
-
-
-
105,4680 = Xs 1,8564 = 0,5H
0,350
0,349869
0,007144
113,7500
113,7074
2,3218
0,400
0,399744
0,010662
130,0000
129,9168
3,4652
0,450
0,449539
0,015176
146,2500
146,1002
4,9322
0,500
0,499219
0,020810
162,5000
162,2462
6,7633
0,550
0,548743
0,027684
178,7500
178,3415
8,9973
0,600
0,598059
0,035917
195,0000
194,3692
11,6730
0,650
0,647105
0,045625
211,2500 = L
210,3091 = X
14,8281 = Y
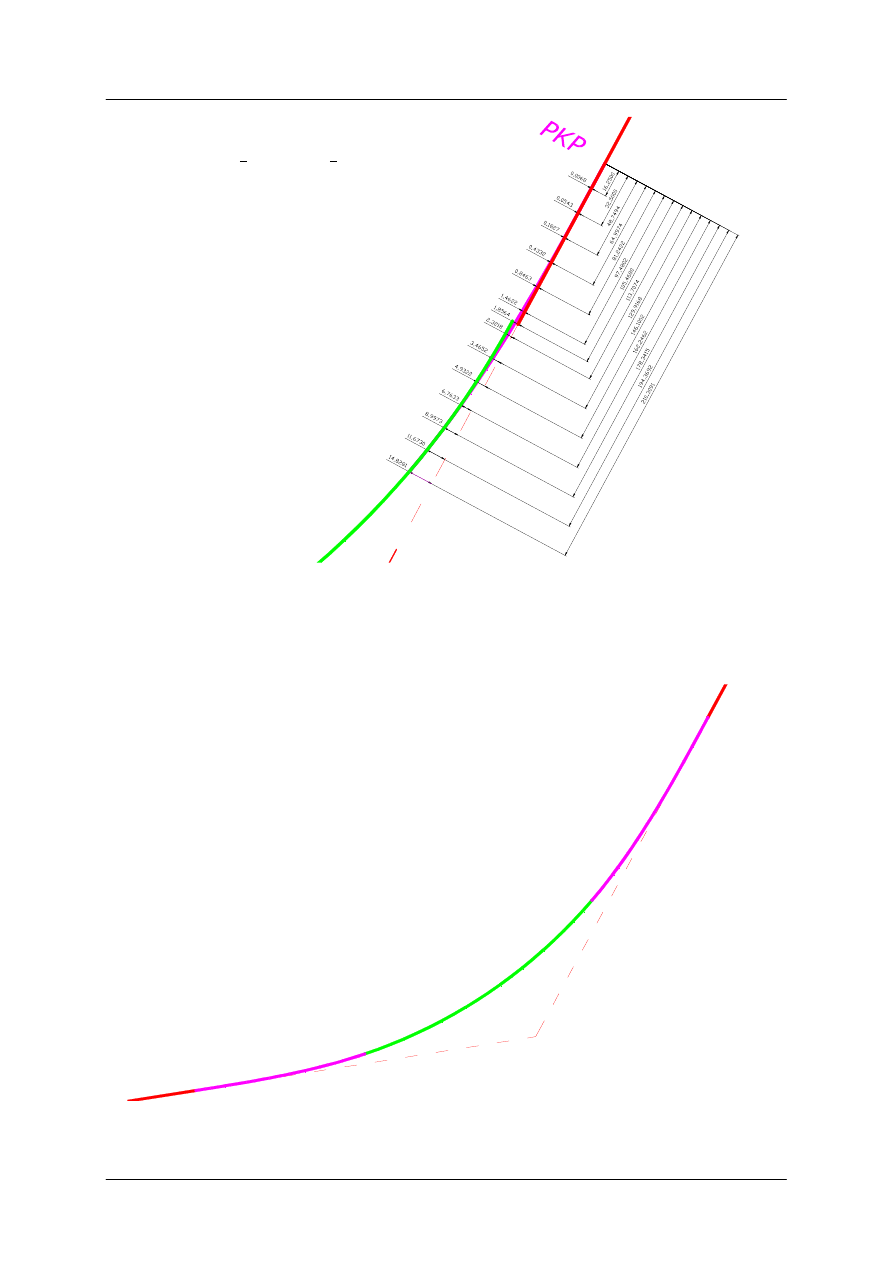
Przykład projektowania łuku poziomego nr 1 z symetrycznymi klotoidami,
łuku poziomego nr 2 z niesymetrycznymi klotoidami i krzywej esowej łączącej oba łuki
Politechnika Białostocka - ZID
- 17 -
mgr inż. Marek Motylewicz
X [m]
Y [m]
1.
16,2500
0,0068
2.
32,5000
0,0543
3.
48,7494
0,1827
4.
64,9974
0,4332
5.
81,2422
0,8463
6.
97,4802
1,4622
7.
105,4680 = Xs
3
1,8564 = 0,5H
3
8.
113,7074
2,3218
9.
129,9168
3,4652
10.
146,1002
4,9322
11.
162,2462
6,7633
12.
178,3415
8,9973
13.
194,3692
11,6730
14.
210,3091 = X
3
14,8281 = Y
3
SK
P
3
3
KŁ
K
2
/ P
KP
3
Rys. 13.
Po wpisaniu klotoid o parametrach A
2
= 290 i A
3
= 325 otrzymujemy rozwiązanie zadania –
układ klotoid niesymetrycznych nr 2 i 3 dla łuku poziomego nr 3 (rys. 14)
K Ł
K
2
/ P
K P
3
PK
P
3
S K
P
3
K
K
P
2
/
P
Ł
K
2
S
K
P
2
P
K
P
2
C
Rys. 14.
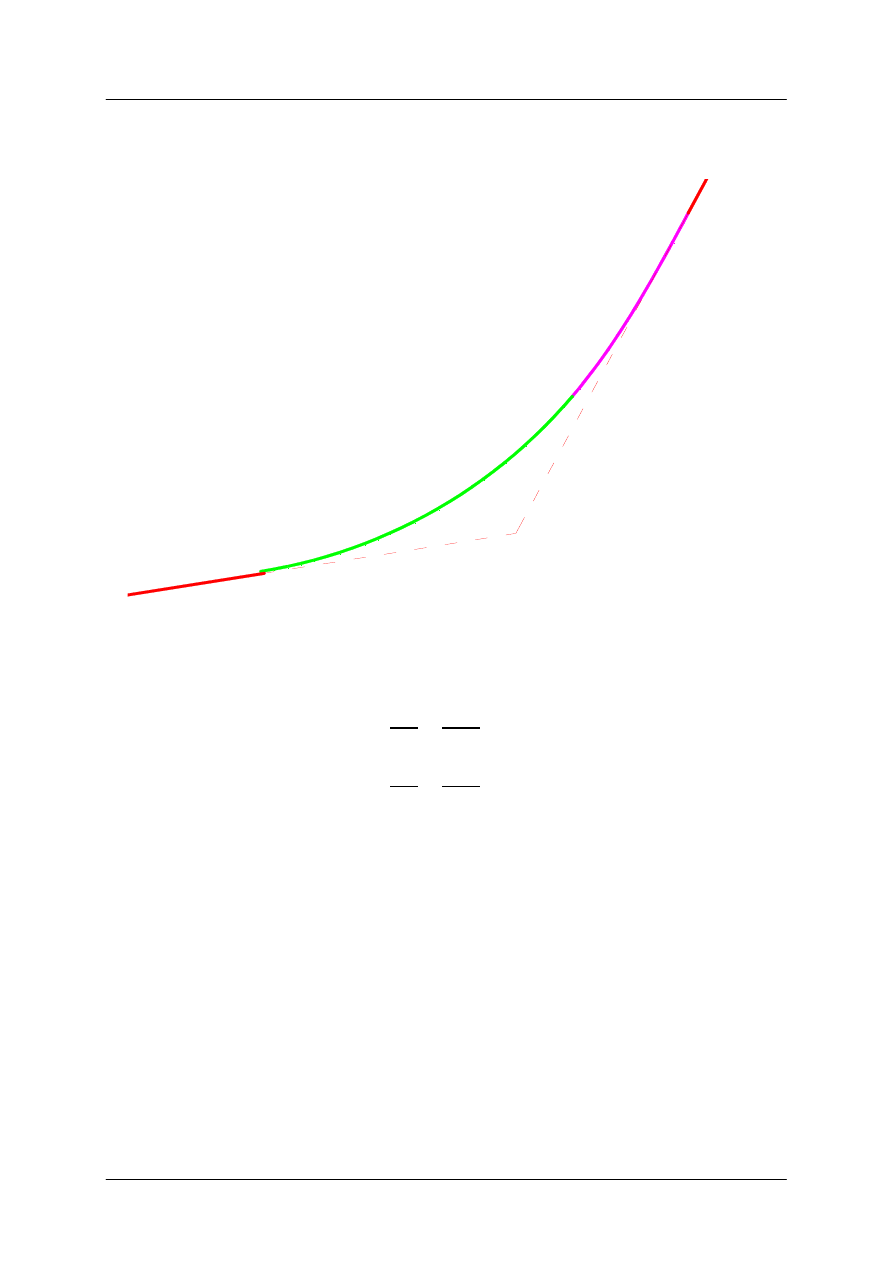
Przykład projektowania łuku poziomego nr 1 z symetrycznymi klotoidami,
łuku poziomego nr 2 z niesymetrycznymi klotoidami i krzywej esowej łączącej oba łuki
Politechnika Białostocka - ZID
- 18 -
mgr inż. Marek Motylewicz
Na potrzeby wpisania krzywej esowej możemy jednak pominąć
wpisywanie krzywej nr 2 pozostawiając odsunięty łuk nr 2 (rys. 15)
C
SK
P
3
PK
P
3
KŁ
K
2
/ P
K P
3
Rys. 15.
5.3.5.
Obliczamy długość klotoid nr 2 i 3 (z podstawowego wzoru klotoidy)
L
ଶ
A
ଶ
ଶ
R
ଵ
290
ଶ
500 168,20 m
L
ଷ
A
ଷ
ଶ
R
ଵ
325
ଶ
500 211,25 m
5.3.6.
Obliczamy styczne T
02
i T
03
układu krzywa przejściowa – łuk poziomy (wg rys. 9)
ଶ
௦ଶᇱ
௦ଶ
ଶ
∆
ଶ
௦ଶ
250,47 84,0208 334,49
ଷ
௦ଷᇱ
௦ଷ
ଶ
∆
ଷ
௦ଷ
247,73 105,4680 353,20
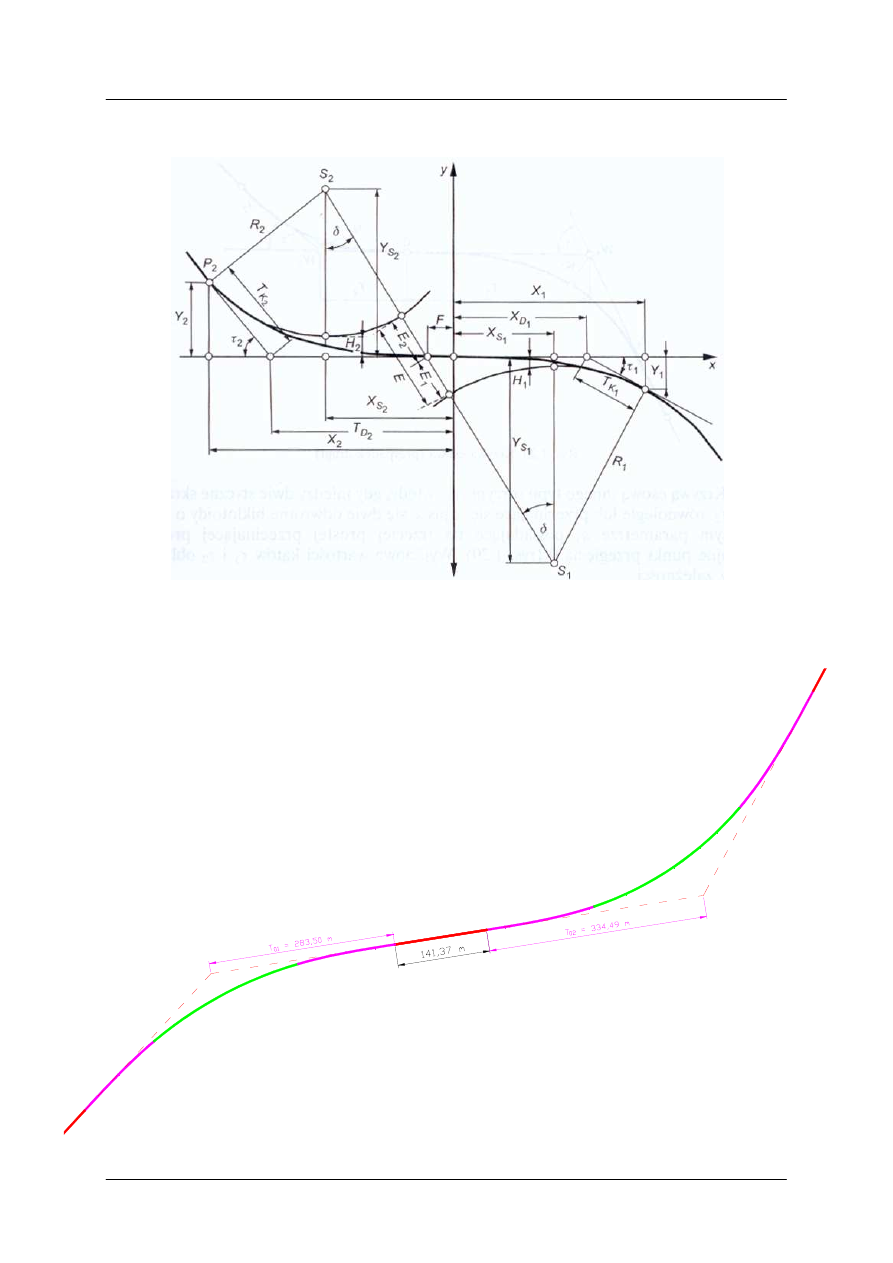
Przykład projektowania łuku poziomego nr 1 z symetrycznymi klotoidami,
łuku poziomego nr 2 z niesymetrycznymi klotoidami i krzywej esowej łączącej oba łuki
Politechnika Białostocka - ZID
- 19 -
mgr inż. Marek Motylewicz
6.
Projektowanie krzywej esowej łączącej łuki poziome nr 1 i nr 2
Rys. 16.
6.1.
Sprawdzenie potrzeby wpisania krzywej esowej
C
P
K
P
2
S
K
P
2
K
K
P
2
/
P
Ł
K
2
S K
P
3
P K
P
3
K Ł K
2
/ P
K P
3
S
K
P
1
a
K
K
P
1
a
/ P
Ł K
1
P K
P
1
a
B
K
Ł
K
1
/
K
K
P
1
b
S
K
P
1
b
P
K
P
1
b
Rys. 17.
Przykład projektowania łuku poziomego nr 1 z symetrycznymi klotoidami,
łuku poziomego nr 2 z niesymetrycznymi klotoidami i krzywej esowej łączącej oba łuki
Politechnika Białostocka - ZID
- 20 -
mgr inż. Marek Motylewicz
T
01
+ T
02
≤ |BC|
Jeżeli warunek jest spełniony nie ma potrzeby projektowania krzywej esowej, lecz
można ją zaprojektować.
283,50 + 334,49 =
617,99 m < 759,36 m
Warunek spełniony. Zadecydowano jednak o wpisaniu krzywej esowej z uwagi na
poprawę płynności trasy (odcinek prosty pomiędzy punktami PKP
1b
oraz PKP
2
miałby
długość 141,37 m)
6.2.
Obliczenie parametru A
E
krzywej esowej
K
Ł
K
2
/
P K
P
3
P K
P
3
SK
P
3
C
D
S
K
P
1
a
K
K
P
1
a
/ P
Ł
K
P
K
P
1
a
A
B
Rys. 18.
Po połączeniu środków okręgów tworzących łuki nr 1 i nr 2 odczytano długość odcinka
E = 44,03 m – odległość pomiędzy okręgami.
Przykład projektowania łuku poziomego nr 1 z symetrycznymi klotoidami,
łuku poziomego nr 2 z niesymetrycznymi klotoidami i krzywej esowej łączącej oba łuki
Politechnika Białostocka - ZID
- 21 -
mgr inż. Marek Motylewicz
2
ଵ
·
ଶ
ଵ
ଶ
2 · 600 · 500
600 500 6000,00
ଵ
ଶ
0,5 · 0,5
ଵ
0,5 ·
ଶ
0,5
600 500 0,5 · 44,03 · 0,5 · 44,03
6000 600 0,5 · 44,03 · 6000 500 0,5 · 44,03
0,02609475
!"#0,02609475 1,494780° 0,02608883 "!%
&
ா
2√3 · · 2√3 · 0,02608883 · 6000 542,24618330
Parametr szukanej krzywej wynosi:
(
ா
&
ா
·
ଵ
·
ଶ
ଵ
ଶ
542,24618330 · 600 · 500
600 500
)*+, ,,*-.*
6.3.
Dla obliczonego parametr A
E
odczytano z tablic wartości elementów klotoid
jednostkowych i przeliczono je na wartości rzeczywiste
•
Ustalenie parametru wejściowego do tablic
/
ଵா
(
ா
ଵ
384,558608
600
0,640931
/
ଶா
(
ா
ଶ
384,558608
500
0,769117
•
Odczytanie z tablic Lipińskiego wartości elementów klotoidy jednostkowej nr 1E
(należy interpolować aby odczytać dokładne wartości) i obliczenie wartości
rzeczywistych
Schemat interpolacyjny 1:
l
τ
∆
x
∆
y
∆
x
s
∆
h
∆
r
∆
0,640000
931
11°44’03”
+2’03”
2’12”
0,637321
+911
979
0,043560
+190
204
0,319553
+463
497
0,010906
+47
51
1,562500
-2270
-2438
0,640931
11°46’06”
0,638232
0,043750
0,320016
0,010953
1,560230
2
·
12
·
·
3
·
ଶ
U
W
A
G
A
:
D
la
łu
k
ó
w
p
o
zi
o
m
y
ch
o
ró
w
n
y
ch
p
ro
m
ie
n
ia
ch
n
ie
o
b
li
cz
a
si
ę
ty
ch
d
an
y
ch
,
a
p
ar
am
et
r
A
o
b
li
cz
a
si
ę
b
ez
p
o
śr
ed
n
io
z
e
w
zo
ru
(
R
=
R
1
=
R
2
):
Przykład projektowania łuku poziomego nr 1 z symetrycznymi klotoidami,
łuku poziomego nr 2 z niesymetrycznymi klotoidami i krzywej esowej łączącej oba łuki
Politechnika Białostocka - ZID
- 22 -
mgr inż. Marek Motylewicz
Tabela 6.1. Wartości klotoidy jednostkowej nr 1E i obliczenie wartości rzeczywistych
Wartości klotoidy
jednostkowej
Wartości rzeczywiste szukanej klotoidy
(wielkości
liniowe
x A
E
)
τ
1Ε
= 11º 46’ 06”
τ
1Ε
= 11,768333º
(przeliczone na wartość dziesiętną)
x
1E
= 0,638232
X
1E
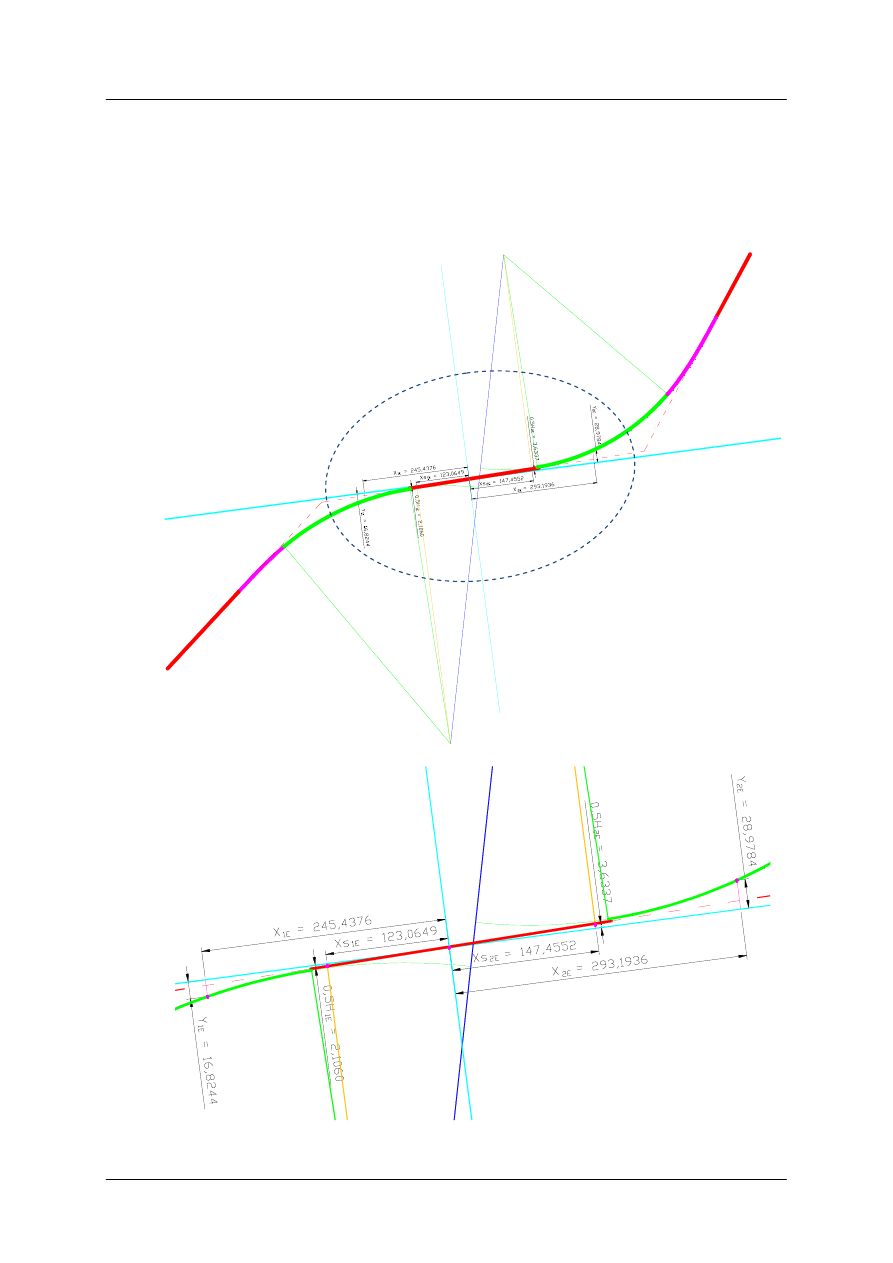
= 245,437610 m
y
1E
= 0,043750
Y
1E
= 16,824439 m
x
s1E
= 0,320016
X
s1E
= 123,064907 m
h
1E
= 0,010953
H
1E
= 4,212070 m
r
1E
= 1,560230
R
1E
= 600,000000 m
l
1E
= 0,640931
L
1E
= 246,475533 m
(długość zaprojektowanej klotoidy)
•
Odczytanie z tablic Lipińskiego wartości elementów klotoidy jednostkowej nr 2E
(należy interpolować aby odczytać dokładne wartości) i obliczenie wartości
rzeczywistych
Schemat interpolacyjny 2:
l
τ
∆
x
∆
y
∆
x
s
∆
h
∆
r
∆
0,769000
117
16°56’28”
+0’19”
2’39”
0,762304
+112
957
0,075321
+34
291
0,383382
+58
493
0,018889
+9
74
1,300390
-198
-1689
0,769117
16°56’47”
0,762416
0,075355
0,383440
0,018898
1,300192
Tabela 6.2. Wartości klotoidy jednostkowej nr 2E i obliczenie wartości rzeczywistych
Wartości klotoidy
jednostkowej
Wartości rzeczywiste szukanej klotoidy
(wielkości
liniowe
x A
E
)
τ
2Ε
= 16º 56’ 74’’
τ
2Ε
= 16,946389º
(przeliczone na wartość dziesiętną)
x
2E
= 0,762416
X
2E
= 293,193636 m
y
2E
= 0,075355
Y
2E
= 28,978414 m
x
s2E
= 0,383440
X
s2E
= 147,455153 m
h
2E
= 0,018898
H
2E
= 7,267389 m
r
2E
= 1,300192
R
2E
= 500,000000 m
l
2E
= 0,769117
L
2E
= 295,770563 m
(długość zaprojektowanej klotoidy)
Przykład projektowania łuku poziomego nr 1 z symetrycznymi klotoidami,
łuku poziomego nr 2 z niesymetrycznymi klotoidami i krzywej esowej łączącej oba łuki
Politechnika Białostocka - ZID
- 23 -
mgr inż. Marek Motylewicz
6.4.
Obliczenie kąta
δδδδ
i długości odcinka F
0
1
௦ଵ
1
௦ଶ
"
ଵ
2
ଵ
"
ଶ
2
ଶ
0
0,320016 0,383440
1,560230 0,010953 1,300192 0,018898 0,243387
0 !"#0,243387 13,67910448°
3 4
௦ଵ
· 0
௦ଵ
ଵ
5
ଵ
· 0
௦ଵ
3 600 4,212070 · 0,243387 123,064907 23,992456
UWAGA
: Dla łuków poziomych o równych promieniach F = 0.
6.5.
Wykreślenie krzywej esowej łączącej dwa łuki poziome o promieniach R
1
i R
2
6.5.1.
Odłożenie obliczonego kąta
δδδδ
od prostej łączącej środki okręgów R
1
i R
2
B
A
P K
P
1
a
K
K
P
1
a
/ P
Ł K
S
K
P
1
a
C
S K
P
3
P K
P
3
K
Ł
K
2
/
P K
P
3
= δ
δ =
Rys. 19.
Przykład projektowania łuku poziomego nr 1 z symetrycznymi klotoidami,
łuku poziomego nr 2 z niesymetrycznymi klotoidami i krzywej esowej łączącej oba łuki
Politechnika Białostocka - ZID
- 24 -
mgr inż. Marek Motylewicz
6.5.2.
Odłożenie obliczonych wartości odcinków H
1E
oraz H
2E
na przedłużeniu prostych
powstałych po odłożeniu kąta
δδδδ
w miejscu przecięcia się tych prostych z łukami
Połączenie końców odcinków H
1E
oraz H
2E
daje nam styczną główną krzywej esowej
(jasnoniebieska linia).
K
Ł
K
2
/
PK
P
3
P K
P
3
S K
P
3
C
D
S
K
P
1 a
K
K
P
1
a
/ P
Ł
K
P
K
P
1
a
A
B
Rys. 20.
Przykład projektowania łuku poziomego nr 1 z symetrycznymi klotoidami,
łuku poziomego nr 2 z niesymetrycznymi klotoidami i krzywej esowej łączącej oba łuki
Politechnika Białostocka - ZID
- 25 -
mgr inż. Marek Motylewicz
6.5.3.
Odłożenie obliczonego odcinka F (wzdłuż stycznej) od punktu przecięcia prostej
łączącej okręgi R
1
i R
2
ze styczną główną w stronę okręgu o większym promieniu
Wyznaczony punkt jest początkiem układu współrzędnych (wyznacza oś Y)
B
A
P
K
P
1
a
K
K
P
1
a
/ P
Ł
K
S
K
P
1
a
D
C
S K
P
3
P K
P
3
K
Ł
K
2
/
PK
P
3
Rys. 21.
Przykład projektowania łuku poziomego nr 1 z symetrycznymi klotoidami,
łuku poziomego nr 2 z niesymetrycznymi klotoidami i krzywej esowej łączącej oba łuki
Politechnika Białostocka - ZID
- 26 -
mgr inż. Marek Motylewicz
6.5.4.
Odłożenie od początku układu współrzędnych odcinków Xs
1E
i 0,5Hs
1E
; X
1E
i Y
1E
oraz Xs
2E
i 0,5Hs
2E
; X
2E
i Y
2E
Po tej czynności mamy już 5 punktów przez które przebiegać będzie krzywa esowa
(łącznie z początkiem układu współrzędnych – punkt przegięcia krzywej)
K
ŁK
2
/
PK
P
3
P K
P
3
S K
P
3
C
D
S
K
P
1 a
K
K
P
1
a
/ P
Ł
K
P
K
P
1
a
A
B
P
K
E
S
K
E
K
K
E
Rys. 22.
Przykład projektowania łuku poziomego nr 1 z symetrycznymi klotoidami,
łuku poziomego nr 2 z niesymetrycznymi klotoidami i krzywej esowej łączącej oba łuki
Politechnika Białostocka - ZID
- 27 -
mgr inż. Marek Motylewicz
6.5.5.
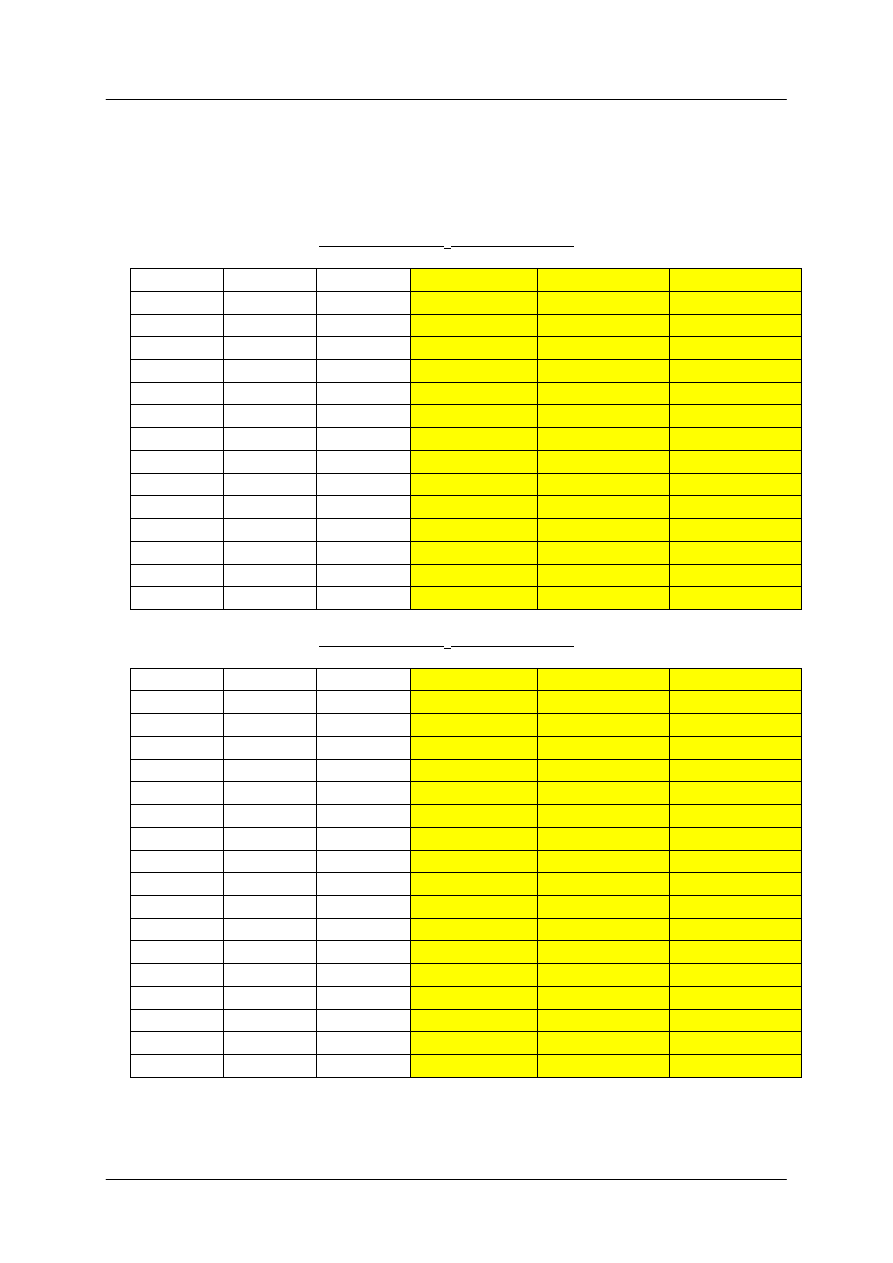
Aby dokładnie wykreślić krzywe odczytujemy z tablic punkty pośrednie
(zakładając krok wartości „l”) i tyczymy kolejne punkty obu klotoid 1E i 2E
metodą rzędnych i odciętych od początku układu współrzędnych
klotoida nr 1E, A
E
= 384,558608 m
l
x
y
L [m] = l · A
X [m] = x · A
Y [m] = y · A
0,050
0,050000
0,000021
19,227930
19,227930
0,008076
0,100
0,100000
0,000167
38,455861
38,455861
0,064221
0,150
0,149998
0,000562
57,683791
57,683022
0,216122
0,200
0,199992
0,001333
76,911722
76,908645
0,512617
0,250
0,249976
0,002604
96,139652
96,130423
1,001391
0,300
0,299939
0,004499
115,367582
115,344124
1,730129
-
-
-
-
123,064907 = Xs 2,106035 = 0,5H
0,350
0,349869
0,007144
134,595513
134,545136
2,747287
0,400
0,399744
0,010662
153,823443
153,724996
4,100164
0,450
0,449539
0,015176
173,051374
172,874092
5,836061
0,500
0,499219
0,020810
192,279304
191,978964
8,002665
0,550
0,548743
0,027684
211,507234
211,023844
10,646121
0,600
0,598059
0,035917
230,735165
229,988737
13,812192
0,640931
0,638232
0,043750
246,475533 = L
245,437610 = X
16,824439 = Y
klotoida nr 2E, A
E
= 384,558608 m
l
x
y
L [m] = l · A
X [m] = x · A
Y [m] = y · A
0,050
0,050000
0,000021
19,227930
19,227930
0,008076
0,100
0,100000
0,000167
38,455861
38,455861
0,064221
0,150
0,149998
0,000562
57,683791
57,683022
0,216122
0,200
0,199992
0,001333
76,911722
76,908645
0,512617
0,250
0,249976
0,002604
96,139652
96,130423
1,001391
0,300
0,299939
0,004499
115,367582
115,344124
1,730129
0,350
0,349869
0,007144
134,595513
134,545136
2,747287
-
-
-
-
147,455153 = Xs 3,633695 = 0,5H
0,400
0,399744
0,010662
153,823443
153,724996
4,100164
0,450
0,449539
0,015176
173,051374
172,874092
5,836061
0,500
0,499219
0,020810
192,279304
191,978964
8,002665
0,550
0,548743
0,027684
211,507234
211,023844
10,646121
0,600
0,598059
0,035917
230,735165
229,988737
13,812192
0,650
0,647105
0,045625
249,963095
248,849798
17,545486
0,700
0,695810
0,056922
269,191026
267,579725
21,889845
0,750
0,744089
0,069916
288,418956
286,145830
26,886800
0,769117
0,762416
0,075355
295,770563 = L
293,193636 = X
28,978414 = Y
Przykład projektowania łuku poziomego nr 1 z symetrycznymi klotoidami,
łuku poziomego nr 2 z niesymetrycznymi klotoidami i krzywej esowej łączącej oba łuki
Politechnika Białostocka - ZID
- 28 -
mgr inż. Marek Motylewicz
S
K
E
K
K
E
P
K
E
X [m]
Y [m]
1.
19,227930
0,008076
2.
38,455861
0,064221
3.
57,683022
0,216122
4.
76,908645
0,512617
5.
96,130423
1,001391
6.
115,344124
1,730129
7.
134,545136
2,747287
8.
147,455153 = Xs
2E
3,633695 = 0,5H
2E
9.
153,724996
4,100164
10.
172,874092
5,836061
11.
191,978964
8,002665
12.
211,023844
10,646121
13.
229,988737
13,812192
14.
248,849798
17,545486
15.
267,579725
21,889845
16.
286,145830
26,886800
17.
293,193636 = X
2E
28,978414 = Y
2E
X [m]
Y [m]
1.
19,227930
0,008076
2.
38,455861
0,064221
3.
57,683022
0,216122
4.
76,908645
0,512617
5.
96,130423
1,001391
6.
115,344124
1,730129
7.
123,064907 = Xs
1E
2,106035 = 0,5H
1E
8.
134,545136
2,747287
9.
153,724996
4,100164
10.
172,874092
5,836061
11.
191,978964
8,002665
12.
211,023844
10,646121
13.
229,988737
13,812192
14.
245,437610 = X
1E
16,824439 = Y
1E
Rys. 23.
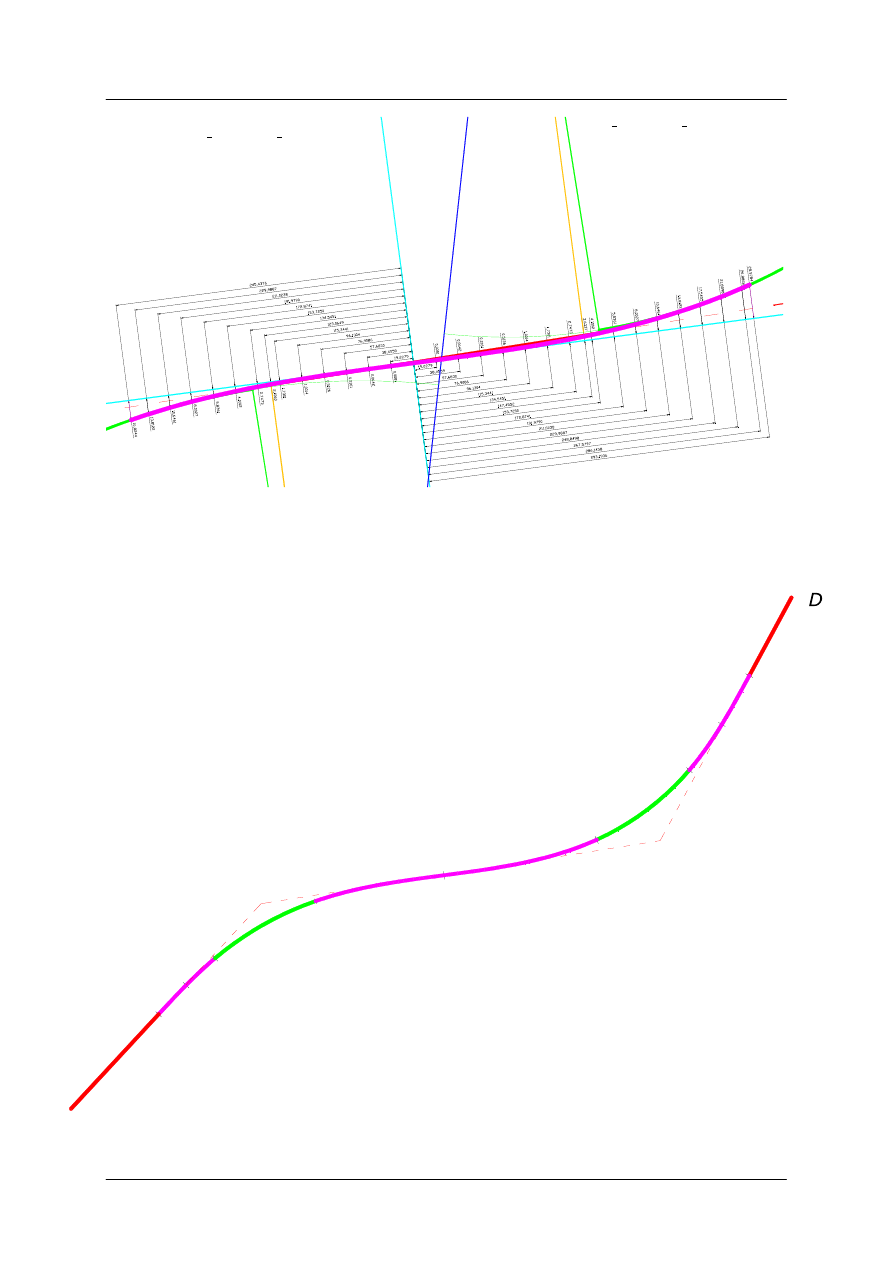
Po wpisaniu obu krzywych 1E i 2E otrzymujemy rozwiązanie zadania – wykreśloną krzywą
esową łączącą łuki poziome nr 1 i nr 2:
K Ł
K
2
/
P K
P
3
P K
P
3
SK
P
3
C
S
K
P
1
a
K
K
P
1
a
/
P
Ł K
P
K
P
1
a
A
B
K
Ł
K
1
/
P
K
E
K
K
E
/
P
Ł
K
2
S
K
E
Rys. 24.
Przykład projektowania łuku poziomego nr 1 z symetrycznymi klotoidami,
łuku poziomego nr 2 z niesymetrycznymi klotoidami i krzywej esowej łączącej oba łuki
Politechnika Białostocka - ZID
- 29 -
mgr inż. Marek Motylewicz
7.
Obliczenie skrócenia trasy po wpisaniu krzywych przejściowych
= ϕ
ϕ =
τ
2Ε
=
= τ
1Ε
δ =
= δ
C
B
Rys. 25.
7.1.
Obliczenia długości łuku poziomego nr 1 po skróceniu
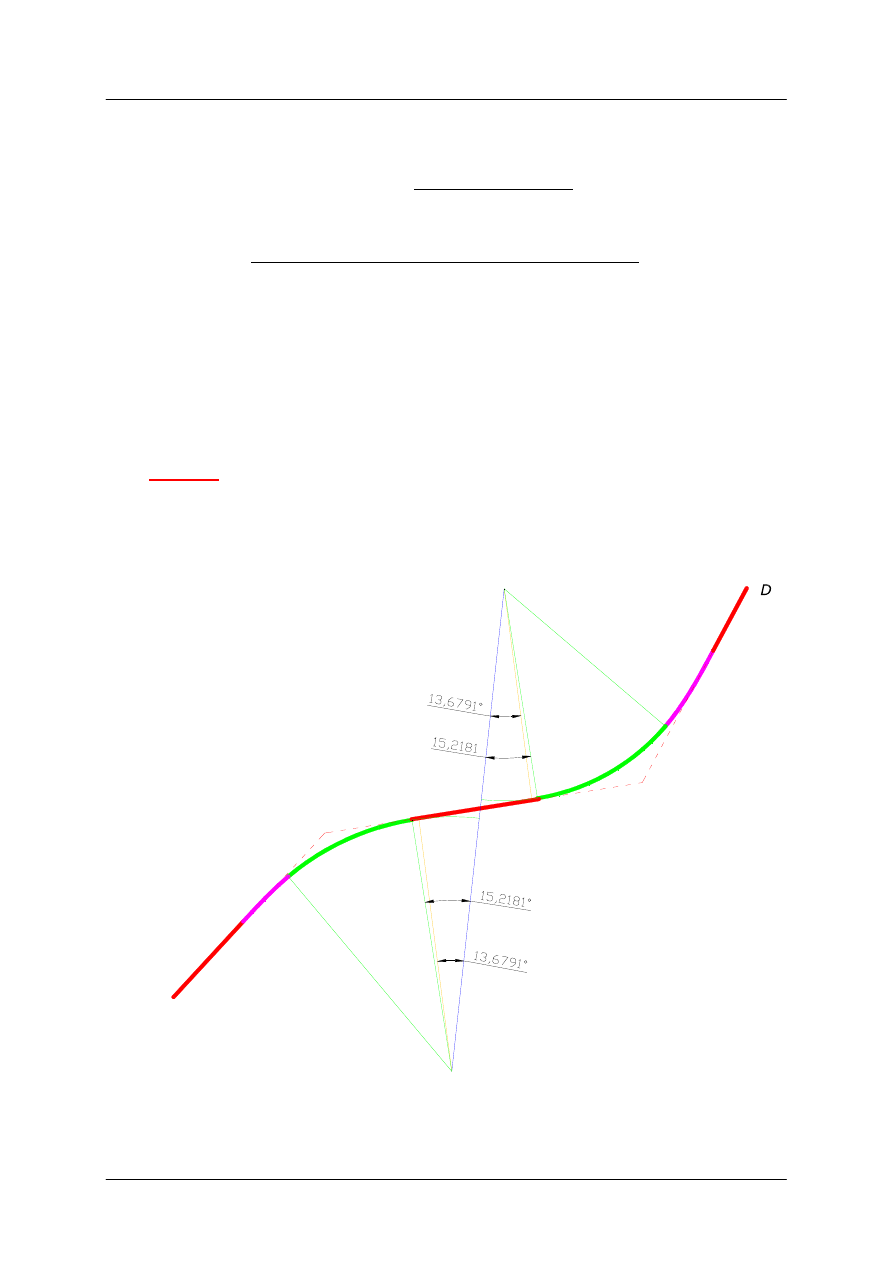
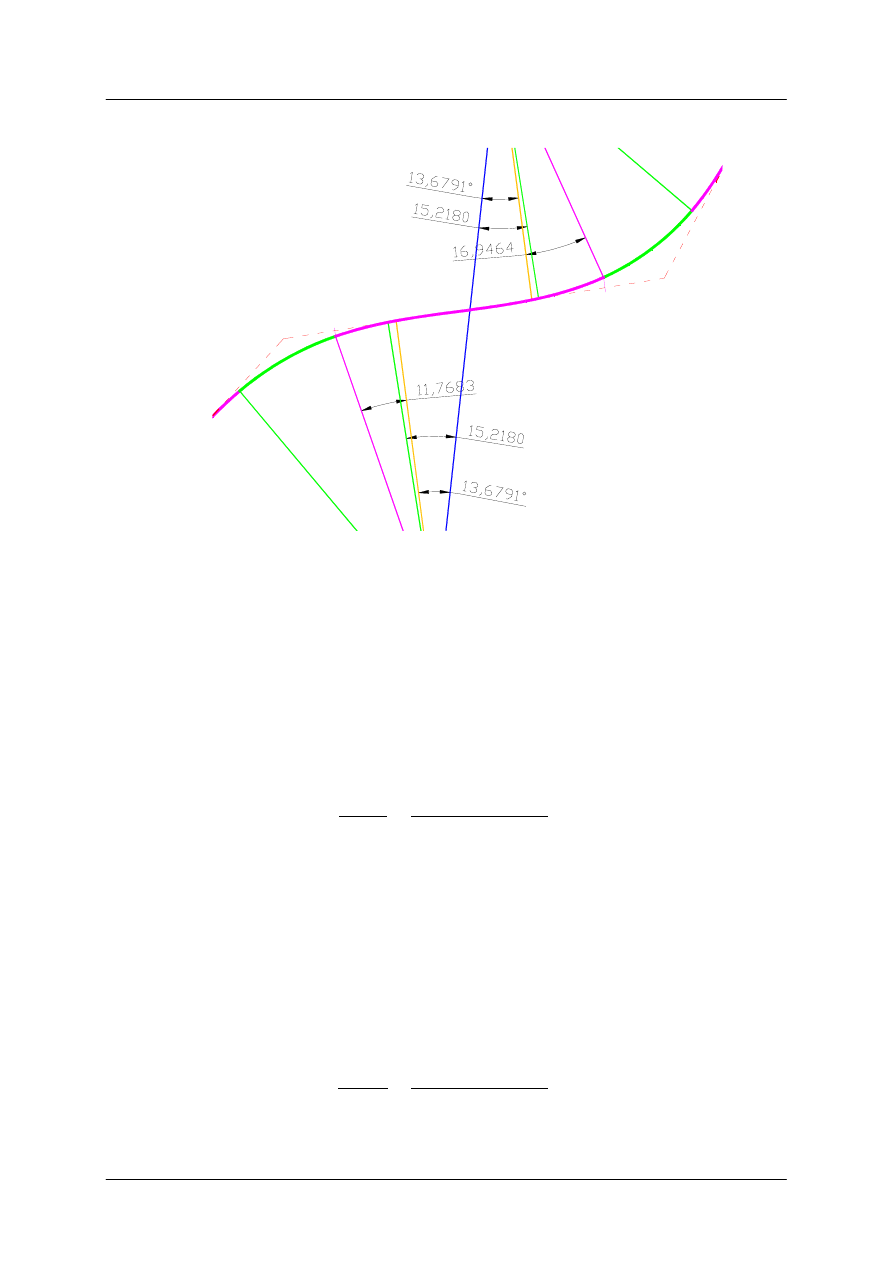
Nowy kąt zwrotu łuku poziomego nr1:
Kąt
ϕ
odczytano z rysunku (kąt pomiędzy prostą łączącą środki okręgów tworzących
łuki poziome nr 1 i nr 2 oraz pomiędzy pierwotnym położeniem promienia R
1
prostopadłego do odcinka |BC|) i wynosi on 15,2180°
38,24 7,1619 11,7683 13,6791 15,2180 20,8487°
Ł
,
180°
600 · · 20,8487°
180°
218,3271
7.2.
Obliczenie długości łuku poziomego nr 2 po skróceniu
Nowy kąt zwrotu łuku poziomego nr2:
Kąt
ϕ
odczytano z rysunku (kąt pomiędzy prostą łączącą środki okręgów tworzących
łuki poziome nr 1 i nr 2 oraz pomiędzy pierwotnym położeniem promienia R
2
prostopadłego do odcinka |BC|) i wynosi on 15,2180°
52,69 12,1036 16,9464 13,6791 15,2180 25,1789°
Ł
,
180°
500 · · 25,1789°
180°
219,7274
Przykład projektowania łuku poziomego nr 1 z symetrycznymi klotoidami,
łuku poziomego nr 2 z niesymetrycznymi klotoidami i krzywej esowej łączącej oba łuki
Politechnika Białostocka - ZID
- 30 -
mgr inż. Marek Motylewicz
7.3.
Obliczenie skrócenia trasy
| | !
Ł
| "| !
!
Ł
|"#| !
௦௧
526,22 208,00 400,45 759,36 208,00 247,60 459,81 520,21 247,60
$
%&'(, )' *
| | !
Ł
,
Ł
,
|"#| !
௪
526,22 283,50 150,00 218,3271 542,2462 219,7274 211,25 520,21 353,20
$
%&'%, +) *
∆
1754,85 1751,28 -, '& *
8.
Zestawienie długości trasy
PPT
= 0,00 m
km 7+200,00
PKP
1a
= |AB| – T
01
= 526,22 – 283,50 = 242,72 m
km 7+442,72
SKP
1a
= PKP
1a
+ 0,5 · L
1
= 242,72 + 0,5 · 150,00 = 317,72 m
km 7+517,72
KKP
1a
/ PŁK
1
= PKP
1a
+ L
1
= 242,72 + 150,00 = 392,72 m
km 7+592,72
SŁK
1
= PŁK
1
+ 0,5 · Ł
1,nowy
= 392,72 + 0,5 · 218,3271 = 501,88 m
km 7+701,88
KŁK
1
/ PKE
= PŁK
1
+ Ł
1,nowy
= 392,72 + 218,3271 = 611,05 m
km 7+811,05
SKE
= PKE + L
1E
= 611,05 + 246,4755 = 857,53 m
km 8+057,53
KKE / PŁK
2
= PKE + L
E
= 611,05 + 542,2462 = 1153,30 m
km 8+353,30
SŁK
2
= PŁK
2
+ 0,5 · Ł
2,nowy
= 1153,30 + 0,5 · 219,7274 = 1263,16 m
km 8+463,16
KŁK
2
/ KKP
3
= PŁK
2
+ Ł
2,nowy
= 1153,30 + 219,7274 = 1373,03 m
km 8+573,03
SKP
3
= KKP
3
+ 0,5 · L
3
= 1373,03 + 0,5 · 211,25 = 1478,66 m
km 8+678,66
PKP
3
= KKP
3
+ L
3
= 1373,03 + 211,25 = 1584,28 m
km 8+784,28
KPT
= PKP
3
+ (|CD| – T
03
) = 1584,28 + (520,21 – 353,20) = 1751,28 m
km 8+951,28
Przykład projektowania łuku poziomego nr 1 z symetrycznymi klotoidami,
łuku poziomego nr 2 z niesymetrycznymi klotoidami i krzywej esowej łączącej oba łuki
Politechnika Białostocka - ZID
- 31 -
mgr inż. Marek Motylewicz
9.
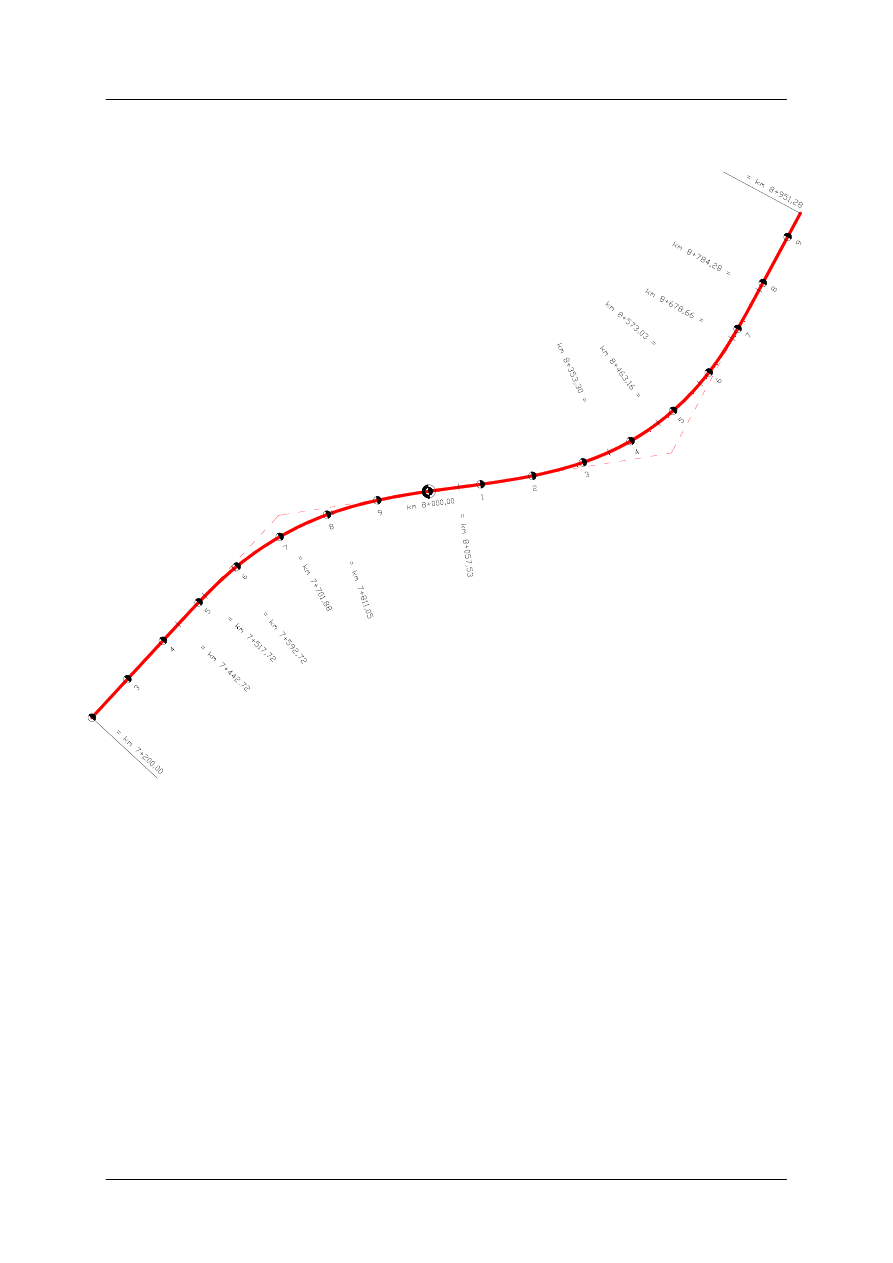
Wytyczenie hektometrów na osi trasy
S
Ł
K
1
S
Ł
K
2
P
K
P
1
a
K P
T
PK
P
3
S K
P
3
K
ŁK
2
/
P K
P
3
K
K
E
/
P
Ł
K
2
S
K
E
K
Ł
K
1
/
P
K
E
K
K
P
1
a
/
P
ŁK
S
K
P
1a
P
P
T
B
A
C
D
Rys. 26.