ANSYS Solutions 2000, Volume 2, Number 1

Ray Browell, ANSYS Product Line Manager

Dr. Guoyo Lin, Senior Member, Technical Staff

The Power of Nonlinear Materials Capabilities

Part 1 of 2 on modeling materials with

nonlinear characteristics

Перевод выполнен Б. Г. Рубцовым

Мощь нелинейных возможностей

Первая часть статьи о моделировании материалов

с нелинейными свойствами

Некоторые пользователи ошибочно полагают, что программа ANSYS является «линейным» кодом. И хотя в основе программы действительно лежат линейные методы расчета, такое представление окажется прискорбным недоразумением, если учесть, какое множество дополнительных возможностей появляется с каждой новой версией. Так, в программе ANSYS на мировом уровне реализовано моделирование контактов с помощью элементов высокого порядка «поверхность-поверхность», учитывающих большие сдвиги и трение. Ниже рассматриваются разнообразные возможности программы ANSYS, которые используются для задания нелинейных свойств материала.

Поведение материала подчиняется весьма сложным закономерностям. Для получения хорошего соответствия между расчетными результатами и фактическим откликом материала используется широкий набор приближений. Чтобы ясно представлять поведение материала, следует, прежде всего, провести классификацию его особенностей.

В данном случае поведение материалов классифицируется таким же образом, как это делается в большинстве традиционных учебных пособий. После того, как осмыслено поведение материала, становится возможной его классификация на основе той или иной иерархии. На самом высшем иерархическом уровне рассматривается, является ли материал линейным или нелинейным (рис. 1). Для линейного материала напряжения пропорциональны деформациям, а его поведение описывается законом Гука. При нелинейном поведении напряжения не остаются пропорциональными деформациям. Хорошо знакомая форма закона Гука для одномерного случая имеет вид

σ = Еε,

где σ - напряжение,

Е - модуль Юнга,

ε - деформация.

Теперь следует установить, является ли поведение материала упругим или неупругим. Упругость представляет собой способность материала сохранять исходную форму после снятия нагрузки. Все материалы, поведение которых подчиняется закону Гука, являются также и упругими, однако не все упругие материалы подчиняются закону Гука. В неупругом материале деформации после снятия нагрузки остаются. Наиболее распространенным видом расчета, при котором учитывается неупругое поведение материала, является рассматриваемый далее пластический анализ.

Следующий шаг состоит в том, чтобы оценить влияние скорости нагружения на поведение материала. Поведение одних материалов зависит от скорости нагружения, поведение других - нет. Последние оказываются нечувствительными к скорости деформации или скорости нарастания нагрузки. Многие металлы ведут себя подобным образом при малых скоростях деформаций и температурах, низких по отношению к температуре плавления. Наоборот, параметры механического отклика для материалов, чувствительных к скорости нагружения, зависят от скорости приложения деформаций или нагрузок. Влияние скорости деформаций становится существенным для многих металлических материалов при высоких температурах (составляющих примерно половину от температуры плавления). Для некоторых уравнений состояния значимость деформаций может существенно меняться в зависимости от скорости, с которой нагружается материал. Это особенно справедливо для уравнений состояния материалов, которые используются при динамических расчетах явными методами. В этой статье не рассматриваются уравнения состояния для материалов при очень высоких скоростях деформации, основное внимание в ней уделено деформациям, которые развиваются в течение длительного время после приложения нагрузки. В большинстве случаев анализ прочности проводится без учета скорости деформации.

Поведение материала	Тип деформации	Скорость деформации	Классификация материала	Закон поведения материала	Метка команды TB	Зависимость от температуры
Линейное	Упругая	Не влияет	Линейно-упругий	Гука (изотропный)	Команда МР	Есть
				Гука (анизотропный)	ANEL	Есть
								Гука (ортотропный)	Команда МР	Есть
Нелинейное	Упругая	Не влияет	Гиперупругий	Муни-Ривлина	MOONEY	Есть
				Арруда-Бойса	BOYCE	Нет
								Блатц-Ко	(установка опций)	Есть
						Мультилинейно-упругий	Мультилинейный упругий	MELAS	Есть
				Влияет	Вязкоупругий	Вязкоупругий	EVIS	Есть (1)
		Неупругая	Не влияет	Изотропно-упрочняющийся	Билинейный изотропный	BISO	Есть
					Мультилин. изотропный	MISO	Есть
								Нелинейный изотропный	NLISO	Есть
								Анизотропный	ANISO	Нет
						Кинемат. упрочняющийся	Билинейный кинематический	BKIN	Есть
						.	Мультилин. кинематический	MKIN/KINH	Есть
								Кабоше	CHABOCHE	Есть
						Комбинация кинематич. и изотропного упрочнения	Кабоше и билинейный изотропный	CHABOCHE и BISO	Есть
							Кабоше и мультилинейный изотропный	CHABOCHE и МISO	Есть
								Кабоше и нелинейный изотропный	CHABOCHE и NLISO	Есть
						Пластический	Друкера-Прагера	DP	Нет
				Влияет	Вязкопластичный	Ползучесть	CREEP	Есть (2)
						Ананд	ANAND
Влияние температуры учитывается в модели материала. (2) Температура учитывается двумя способами: (а) уравнением ползучести; (б) уравнением ползучести и заданием таблицы.			Комбинация ползучести и изотроп. упрочнения	Ползучесть и билинейный изотропный	CREEP и BISO	Есть
							Ползучесть и мультилинейн. изотропный	CREEP и MISO	Есть
								Ползучесть и нелинейный изотропный	CREEP и NLISO	Есть

Рис. 1 Классификация материалов и опции программы ANSYS 5.6

Теперь можно приступить к раскрытию содержания терминов в графе «Классификация материала», относящихся к линейно-упругому материалу, гиперупругой среде и различным типам пластичности.

Линейная упругость

Линейная упругость и расчеты на ее основе являются самыми распространенными типами поведения материала и анализа прочности. Линейно-упругий материал подчиняется соотношениям закона Гука и не сохраняет деформаций после снятия нагрузки. В программе ANSYS реализованы три вида линейно-упругого поведения материала: изотропное, анизотропное и ортотропное. Изотропный материал проявляет одни и те же механические свойства во всех направлениях. Это значит, что модуль упругости для направлений x, y, z одинаков. При анизотропном поведении механические свойства материала различаются для разных направлений. К анизотропным относятся такие материалы, как древесина или композит со стекловолокном. В особом случае, когда свойства материала обладают симметрией относительно трех ортогональных плоскостей (плоскостей, расположенных под углом 90 градусов друг к другу), материал является ортотропным. Некоторые композитные материалы, например, армированный волокном эпоксипласт, могут быть ортотропными.

Гиперупругость

К гиперупругим материалам, иногда называемым эластомерами, относятся материалы, обладающие свойствами резины. В частности, они могут претерпевать большие деформации (обычно от 100 до 200 процентов и более) и возвращаться в исходное состояние

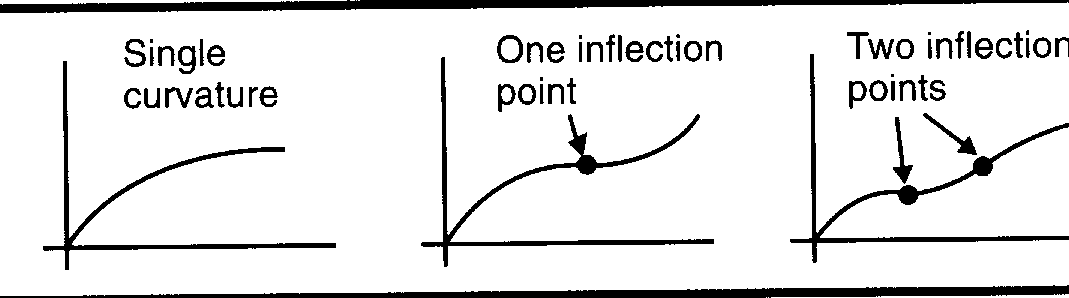
или очень близкое к нему. Диаграмма растяжения гиперупругих материалов может быть весьма сложной и иметь одну или две точки перегиба (рис. 2). Автомобильные шины, резиновые ленты, поливочные шланги и подошва некоторых видов обуви сделаны из гиперупругих материалов. В программе ANSYS для гиперупругих материалов можно задать уравнение состояния трех видов: Муни-Ривлина, Арруда-Бойса и Блатц-Ко.

Закон Муни-Ривлина является наиболее употребительным при моделировании гиперупругих материалов. Его соотношения базируются на выражении для функции плотности энергии деформаций, которая учитывает до девяти параметров в виде комбинации инвариантов тензора деформаций. В программе ANSYS реализованы три варианта закона с числом констант материала, равным двум, пяти и девяти. Значения этих констант обычно определяются при аналитическом описании экспериментальных данных. В программе ANSYS есть возможность вычислить нужные параметры путем обработки экспериментальных данных и получить графическое представление исходной информации. Версия 5.6 программы располагает двумя вариантами проверки состоятельности введенных параметров. Первый вариант состоит в проверке шести типовых соотношений для напряжений (одноосное растяжение-сжатие, равномерное двухосное растяжение-сжатие и плоское растяжение-сжатие). Еще одна проверка (поэлементная) выполняется во время решения с использованием параметров фактического трехмерного напряженного состояния. Этот вариант проверки выполняется по выбору пользователя.

Модель материала Арруда-Бойса впервые появилась в версии 5.6. Эта физически обоснованная модель может использоваться для описания значительного растяжения резиновых материалов. Предложенная в 1993 году, модель построена с учетом физики полимеров и статистической механики. Эта модель материала основана на представлении основной макромолекулярной структуры резины в виде сцепленных петель-«восьмерок» и негауссовского характера отклика индивидуальных цепочек.

Уравнение состояния Блатц-Ко пригодно для испытывающих сжатие материалов типа пенополиуретана. Эта модель активизируется выбором элемента HYPER84 или HYPER86 и не требует использования команды ТВ.

Мультилинейная упругость

С традиционной точки зрения мультилинейная упругость не является реологической моделью. В действительности она представляет собой расширение закона Гука и предполагает кусочно-линейное, абсолютно упругое поведение материала. В силу кусочной линейности модель описывает нелинейный отклик материала. В настоящее время наличие большого числа разнообразных уравнений состояния ограничивает применимость модели мультилинейной упругости.

Вязкоупругость

Вязкоупругий материал рассматривается первым в ряду материалов, классифицируемых как чувствительные к скорости деформации. По определению материал, чувствительный к скорости деформации, имеет отклик, хоть в малой степени зависящий от времени. Деформация вязкоупругого материала состоит из двух обратимых частей: мгновенно исчезающей и зависящей от времени. Мгновенно исчезающая часть соответствует обычной линейно-упругой модели. Часть деформации, зависящая от времени, характерна для среды, механическим аналогом которой является параллельное соединение пружины и демпфера (амортизатора). Реализованная в программе модель вязкоупругой среды обычно используется для описания деформированного

Рис. 2

состояния материалов типа стекла. Такие материалы превращаются в вязкие жидкости при высоких температурах, а при обычных ведут себя как твердые тела.

Нелинейные, неупругие,

нечувствительные к скорости деформации материалы

Основная часть материалов, относящихся к этой классификации, проявляет свойства пластичности, которые не зависят от всестороннего, гидростатического давления. В данную категорию попадают многие металлы при обычных температурах (т.е. температурах, не превышающих половины от температуры плавления). Чтобы понять конкретные уравнения состояния, следует сначала рассмотреть общее в пластическом поведении среды.

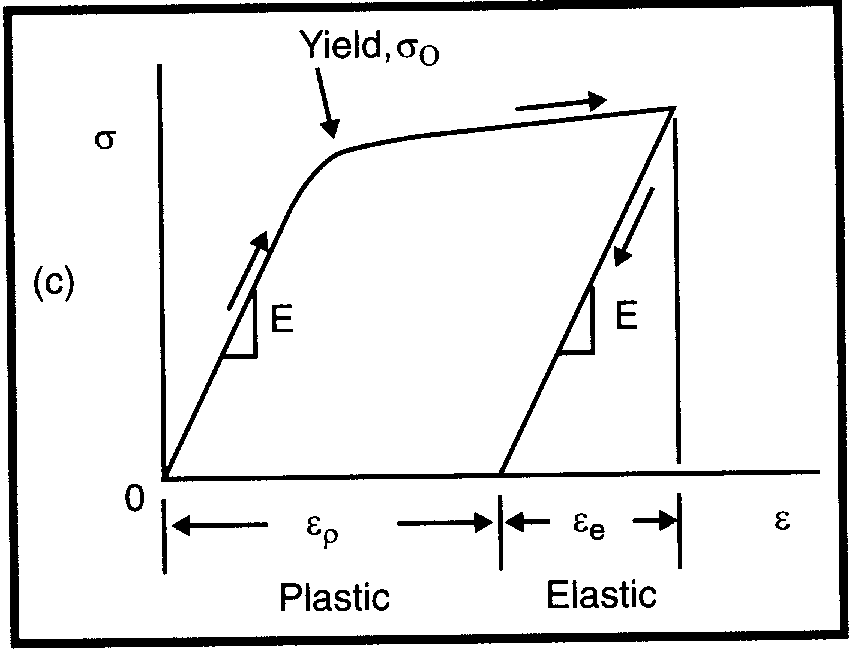
Пластические деформации не исчезают после снятия нагрузки и, таким образом, являются остаточными. Характерно, что после появления пластических деформаций достаточно небольшого увеличения напряжений для существенного роста деформаций. Это явление называется текучестью, а соответствующее напряжение называется напряжением текучести (рис. 3).

Рис. 3

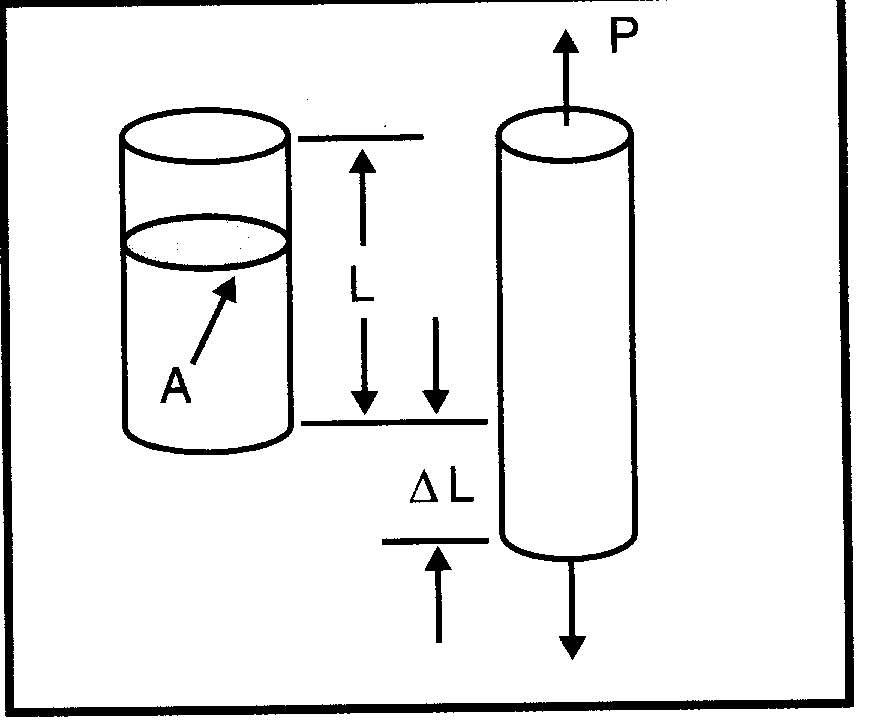
Рис. 4

Существуют так называемые инженерные напряжения и соответствующие им инженерные деформации, а также истинные напряжения и деформации. Инженерные деформации иногда рассматриваются как «малые» деформации. В одноосном случае (рис. 4) инженерные напряжения и деформации определяются следующим образом:

σ_engineering = P/A, ε_engineering = ΔL/L,

где σ_engineering - инженерные напряжения,

P - приложенная нагрузка,

A - площадь поперечного

сечения,

ε_engineering - инженерные деформации,

ΔL - изменение длины,

L - начальная длина.

При работе с программой ANSYS, начиная с версии 5.0, требуется вводить значения напряжений и деформаций в виде истинных напряжений и деформаций. Для одномерного случая истинные деформации подсчитываются по формуле

ε_true = ln(L/L_o),

где ε_true - истинные деформации,

L - текущее значение длины

(обратите внимание!),

L_o - начальная длина.

Из этого соотношения видно, почему истинные деформации иногда называются логарифмическими. Такие деформации еще называют естественными. Истинная деформация представляет собой среднюю величину деформации при изменении длины стержня от исходного значения до текущего. Чтобы перейти от инженерных напряжений и деформаций к истинным, можно использовать следующие соотношения:

σ_true = σ_engineering(1 + ε_engineering),

ε_true = ln(1 + ε_engineering),

где σ_true­ - истинные напряжения.

Эти соотношения применимы только для несжимаемого материала (другими словами, для случая, когда всестороннее давление не вызывает пластического отклика материала).

При малых деформациях значения инженерных и истинных параметров почти идентичны (табл. 1). Однако по мере возрастания деформаций эти значения расходятся. При этом угловой коэффициент диаграммы в области истинных пластических деформаций положителен, а для инженерных деформаций - отрицателен (рис. 5). Кроме того, протяженность диаграммы истинных напряжений существенно меньше. Условимся все упоминаемые далее в статье напряжения и деформации рассматривать как истинные.

После общего определения феномена пластичности и способов исчисления деформаций можно перейти к рассмотрению различий в пластическом поведении среды.

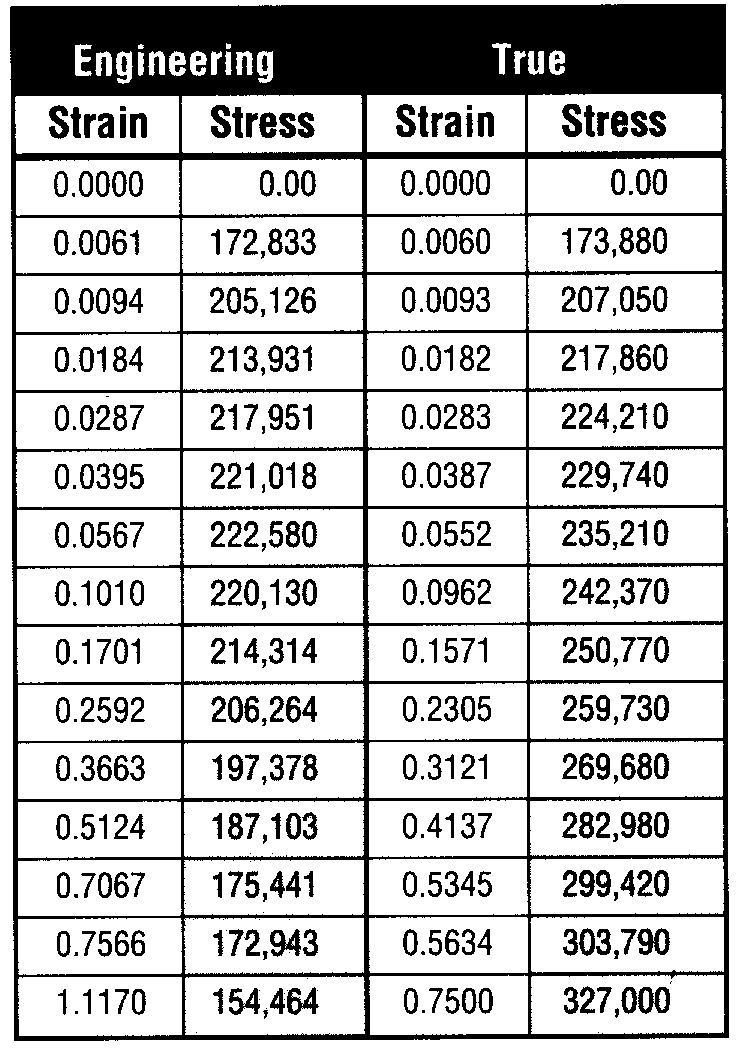
Таблица 1. Сравнение значений инженерных

и истинных деформаций и напряжений

Пластичность материала проявляется как его «текучесть». В одномерном случае текучесть возникает при достижении напряжениями величины предела текучести. Для более сложных напряженных состояний требуется некий метод, чтобы на основе различных компонент напряжений получить критерий, который можно было бы сопоставить с напряжениями текучести для одноосного случая. Широко используется энергетический критерий формоизменения, часто называемый критерием Мизеса. Независимо от того, какой конкретный метод используется, предел текучести материала при простом растяжении преобразуется в кривую текучести для двумерного напряженного состояния и в поверхность текучести - для трехмерного. После достижения начала пластичности напряжения должны возрастать, чтобы процесс пластического деформирования развивался (рис. 3). Такое возрастание напряжений называется упрочнением.

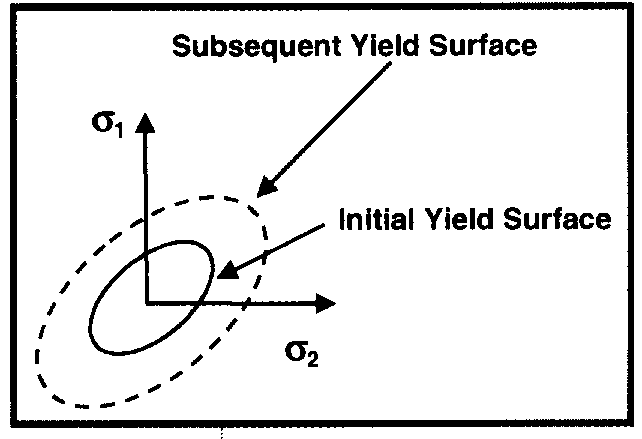
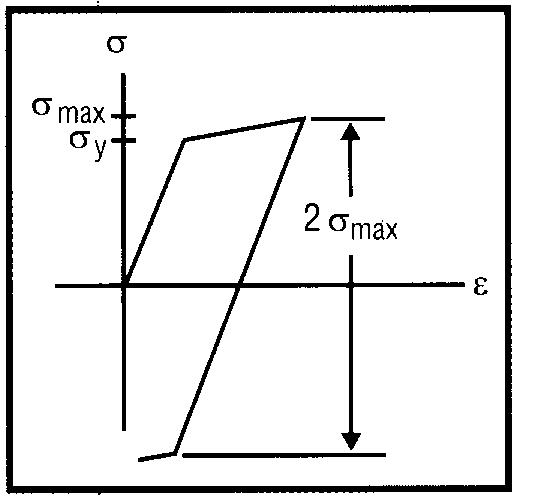
Упрочнение соответствует такому изменению поверхности текучести в процессе нагружения, при котором выполняются условия существования дальнейших пластических деформаций. Имеют место два основных типа упрочнения: изотропное и кинематическое. В случае изотропного упрочнения поверхность текучести расширяется равномерно во всех направлениях и сохраняет исходное положение своего центра. Предполагается, что механизм упрочнения действует одинаково как при растяжении, так и при сжатии (рис. 6). При изотропном упрочнении абсолютные величины предела текучести при сжатии и растяжении всегда равны. Увеличение напряжений сверх предела текучести приводит к росту предела пропорциональности при разгрузке, при этом размах упругих напряжений в два раза превосходит величину наибольших достигнутых напряжений (рис. 7).

В случае кинематического упрочнения поверхность текучести смещается, не меняя размеров (рис. 8). Если образец сначала растянуть, затем снять нагрузку, а потом к образцу приложить сжимающую нагрузку, то предел текучести при сжатии будет меньше, чем при растяжении. Уменьшение предела текучести при сжатии в точности равно превышению исходного предела текучести при растяжении. Это явление называется эффектом Баушингера, который имеет место в металлах при смене знака нагружения (рис. 9). Учет эффекта Баушингера важен при расчетах циклических нагрузок, сопровождающихся пластическими деформациями, как в случае моделирования малоцикловой усталости при относительно низких напряжениях или деформациях, а также в случае непропорционального нагружения. Вообще говоря, изотропное упрочнение рекомендуется использовать при учете конечных деформаций (больших истинных деформаций, превосходящих в металлах 5-10 процентов) в случае пропорционального, непериодического нагружения. Кинематическое упрочнение следует использовать в случае непропорционального или циклического нагружения, когда истинные деформации относительно малы (менее 5-10 процентов для металлов).

Существуют еще два варианта нагружения, важных с точки зрения циклического пластического деформирования: нарастание деформаций с каждым циклом по типу храповика (ratcheting) и так называемая «приспособляемость» (shakedown). При кинематическом упрочнении размах упругих напряжений, сопровождающих разгрузку, равен удвоенной величине предела текучести. Если образец при растяжении нагружается выше напряжений текучести, возникает пластическое состояние. Поверхность текучести перемещается, чтобы могли реализоваться упругие напряжения разгрузки, и это приводит к снижению уровня напряжений текучести при сжатии. Если теперь образец сжать той же нагрузкой, что и при растяжении, то поверхность текучести сместится вновь - для выполнения условий разгрузки. При уменьшении нагрузки до нуля завершается один полный цикл нагружения. Поверхность текучести смещается в область сжатия. Если вновь растянуть образец первоначальным усилием, то напряжения текучести снова будут превышены, что приведет к дополнительным пластическим деформациям. Эти деформации называются циклическим приращением деформаций. Они обусловлены сочетанием нагрузки, при которой превышаются начальные напряжения текучести, циклическим приложением нагрузки и наличием эффекта Баушингера. Следует заметить, что при учете анизотропии материала размах напряжений разгрузки мог бы оказаться равным удвоенной величине максимума достигнутых напряжений, и никакой пластичности после снятия растягивающей нагрузки не возникло бы.

Когда нагрузка не является знакопеременной в чистом виде, а приращения деформаций за цикл контролируемого нагружения остаются примерно постоянными в каждом последующем цикле, то говорят, что рост дефор-

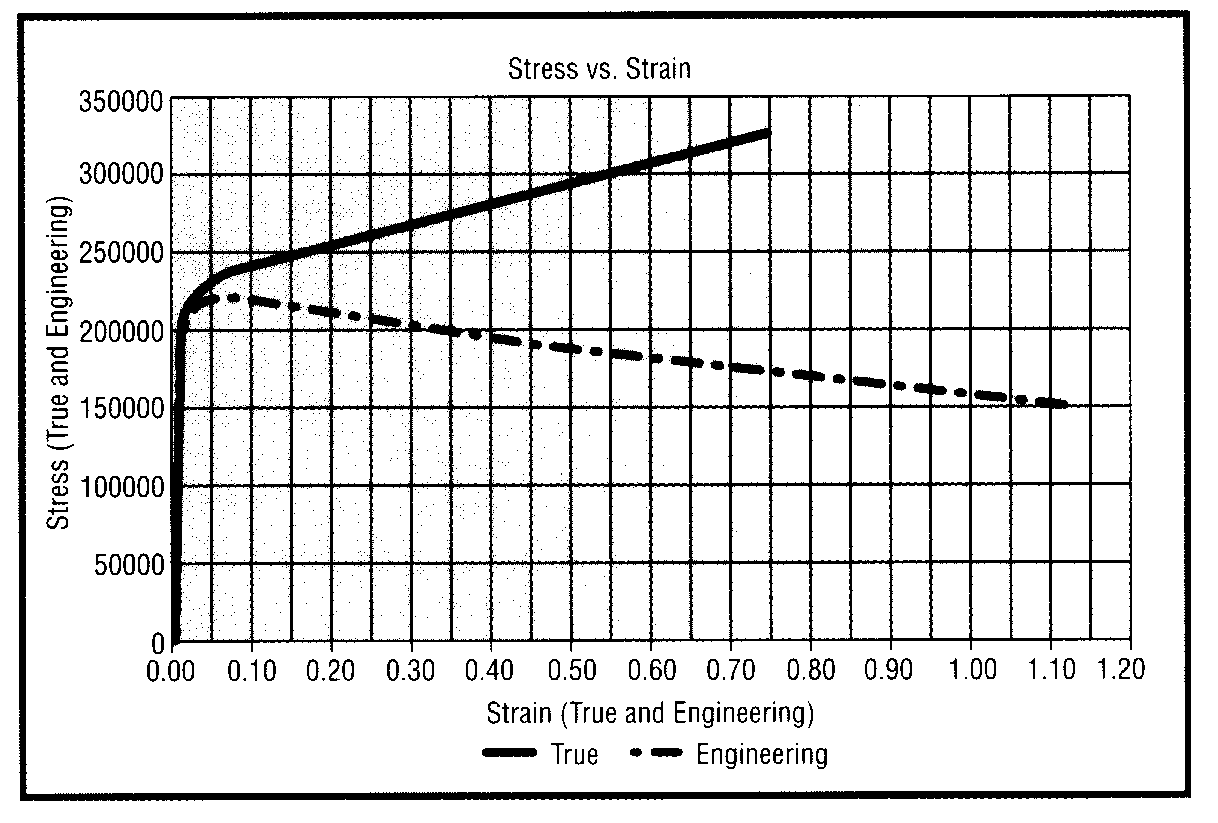
Рис. 5

маций происходит по типу храповика (рис.10). Если же нагрузка по-прежнему не является знакопеременной в чистом виде, но приращения деформаций за цикл нагружения уменьшаются в каждом последующем цикле, то имеет место «приспособляемость».

Изотропное упрочнение

При изотропном упрочнении поверхность текучести расширяется равномерно во всех направлениях и сохраняет исходное положение своего центра. Это показывает, что механизм упрочнения действует одинаково при растяжении и сжатии.

В случае билинейного изотропного упрочнения пластический участок диаграммы деформирования имеет постоянный наклон.

Как следует из названия, мультилинейное изотропное упрочнение характеризуется кусочно-линейным описанием пластической части диаграммы деформирования.

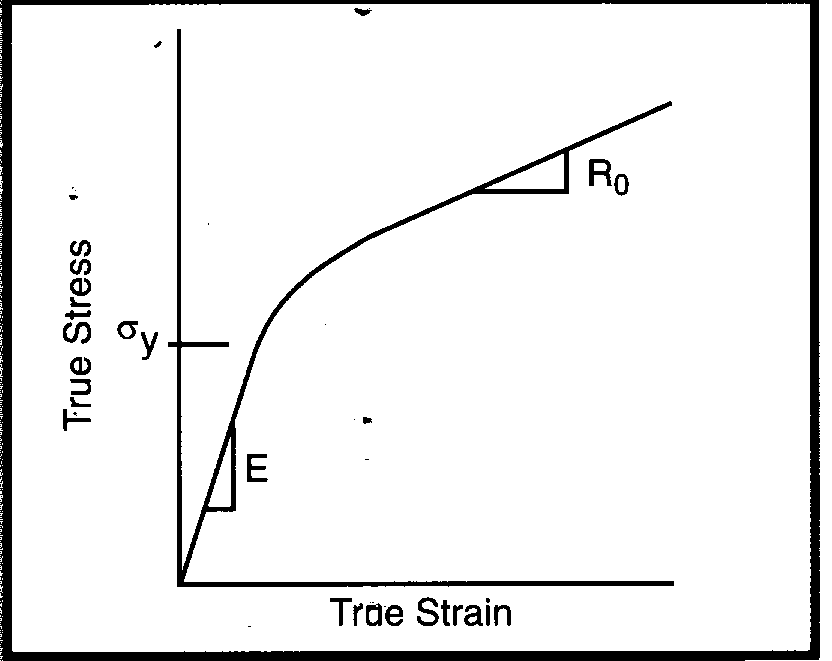
Форма задания нелинейного изотропного упрочнения основана на уравнении состояния материала, предложенного Voce. Это вариант мультилинейного изотропного упрочнения, в котором к линейному слагаемому добавлен экспоненциальный член, описывающий упрочнение. Преимуществом модели является то, что поведение материала задается гладкой функцией, зависящей от четырех констант. Эти постоянные можно получить с помощью диаграммы растяжения для материала. Такая модель применима только для материалов, диаграммы которых имеют плавный переход от прямой, соответствующей модулю упругости, к участку постоянного упрочнения (рис. 11).

Анизотропное упрочнение используется для материалов, поведение которых различно в направлениях осей x, y, z, а также при растяжении, сжатии и сдвиге. Применимо для металлов, подвергнутых некоторым предварительным деформациям (например, при прокатке).

Рис. 6

Рис. 7

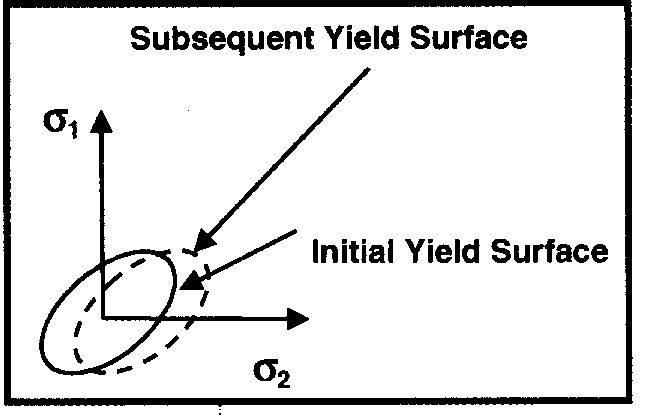
Рис. 8

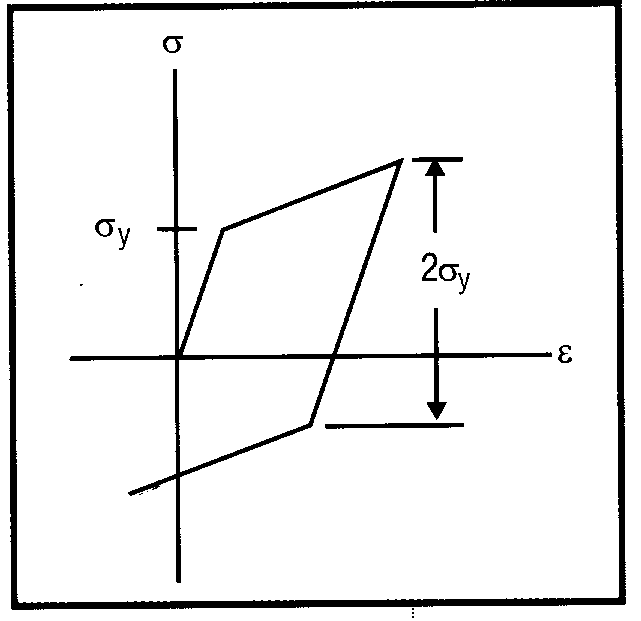
Рис. 9

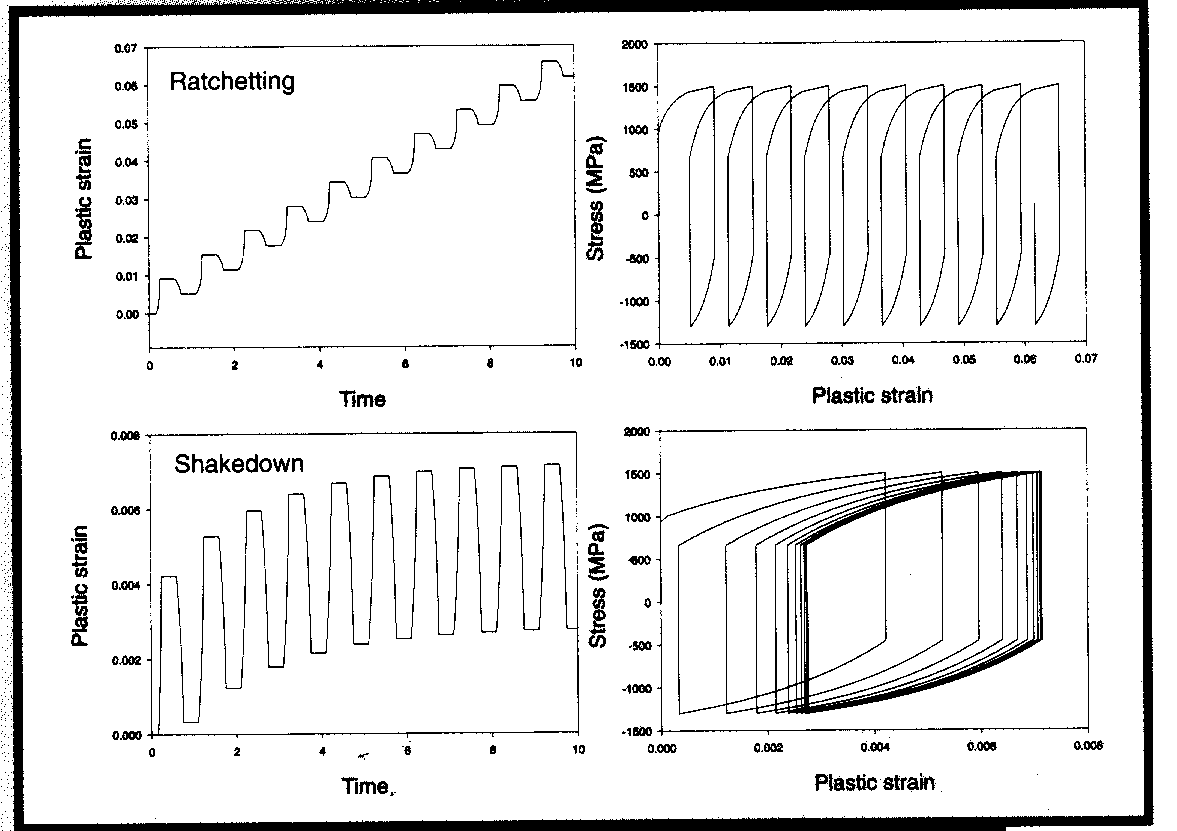
Рис. 10

Рис. 11

Напряжения текучести и углы наклона участков упрочнения не являются независимыми.

Кинематическое упрочнение

При кинематическом упрочнении поверхность текучести смещается без изменения размеров. Учитывается эффект Баушингера, область упругой разгрузки всегда равна удвоенной величине начального предела текучести.

Билинейное кинематическое упрочнение описывает простую модель материала с постоянным наклоном пластического участка диаграммы деформирования. Это разумное приближение, если одноосное поведение материалов в пластической области можно линеаризовать. Следовательно, такая модель может быть рекомендована для расчетов при малых деформациях, в которых амплитуды деформаций или напряжений относительно невелики, например, при анализе малоцикловой усталости.

Как следует из названия, мультилинейное кинематическое упрочнение характеризуется кусочно-линейным описанием пластической части диаграммы деформирования. В новой версии программы ANSYS опция мультилинейного кинематического упрочения KINH основана на том же самом уравнении состояния материала и ведет себя аналогично прежнему варианту MKIN; однако ограничения, касающиеся объема вводимых в программу данных, различаются существенно. Для опции KINH максимальное число кривых зависимостей свойств материала от температуры составляет 40, тогда как для MKIN - только пять. Кроме того, увеличено число точек для представления данных каждой кривой. Для варианта KINH максимальное число точек описания одной температурной кривой равно 20, а для MKIN - пять.

При выборе опции Chaboche используется модель нелинейного кинематического упрочнения Кабоше - многокомпонентная модель, позволяющая совместить несколько моделей кинематического упрочнения. Подобно опциям билинейного и мультилинейного кинематического упрочнения закон Кабоше описывает монотонное упрочнение и эффект Баушингера. В отличие от других вариантов кинематического упрочнения эту опцию можно использовать для анализа с учетом больших деформаций. С ее помощью можно моделировать отклик систем при росте деформаций по типу храповика или с учетом приспособляемости.

Сочетание кинематического и изотропного упрочнения

Кинематическое упрочнение рекомендуется использовать для проведения циклического пластического анализа, при этом, однако, поверхность текучести может только смещаться. Изотропное упрочнение меняет размеры поверхности текучести, но только без ее смещения, что препятствует определению дополнительного приращения деформаций при циклическом нагружении. У некоторых материалов при циклическом нагружении обнаруживается изменение значений как напряжений текучести, так и приращения деформаций за цикл. Более точное описание стадии упрочнения материалов достигается в модели, объединяющей независимые варианты кинематического и изотропного упрочнения в виде поверхности текучести, которая жестко смещается и равномерно расширяется. Эта модель улучшает моделирование таких сложных циклических явлений, как циклическое упрочнение и разупрочнение. В программе ANSYS 5.6 эти сложные типы поведения материала моделируются путем комбинации кинематического и изотропного упрочнения.

Такое сочетание может рассматриваться в виде модели со свойствами, которые описывают как кинематическое, так и изотропное упрочнение. С точки зрения весьма упрощенного подхода комбинация кинематического и изотропного поведения материала для одномерного случая выражается следующим образом:

Область разгрузки = 2(σ_yield + С(σ_maximum - σ_yield)),

где σ_yield - начальный предел текучести,

σ_maximum - максимальное значение

действующих напряжений,

С - коэффициент упрочнения, 0 ≤ С ≤ 1;

при С = 0 упрочнение кинематическое,

при С= 1 упрочнение изотропное,

при 0 < С < 1 упрочнение комбинированное.

Данная форма записи приведена исключительно с целью иллюстрации. В

случае реального объемного напряженного состояния комбинация такого рода происходит естественным образом при решении уравнений, описывающих пластическое поведение, и заранее заданный коэффициент упрочнения не используется.

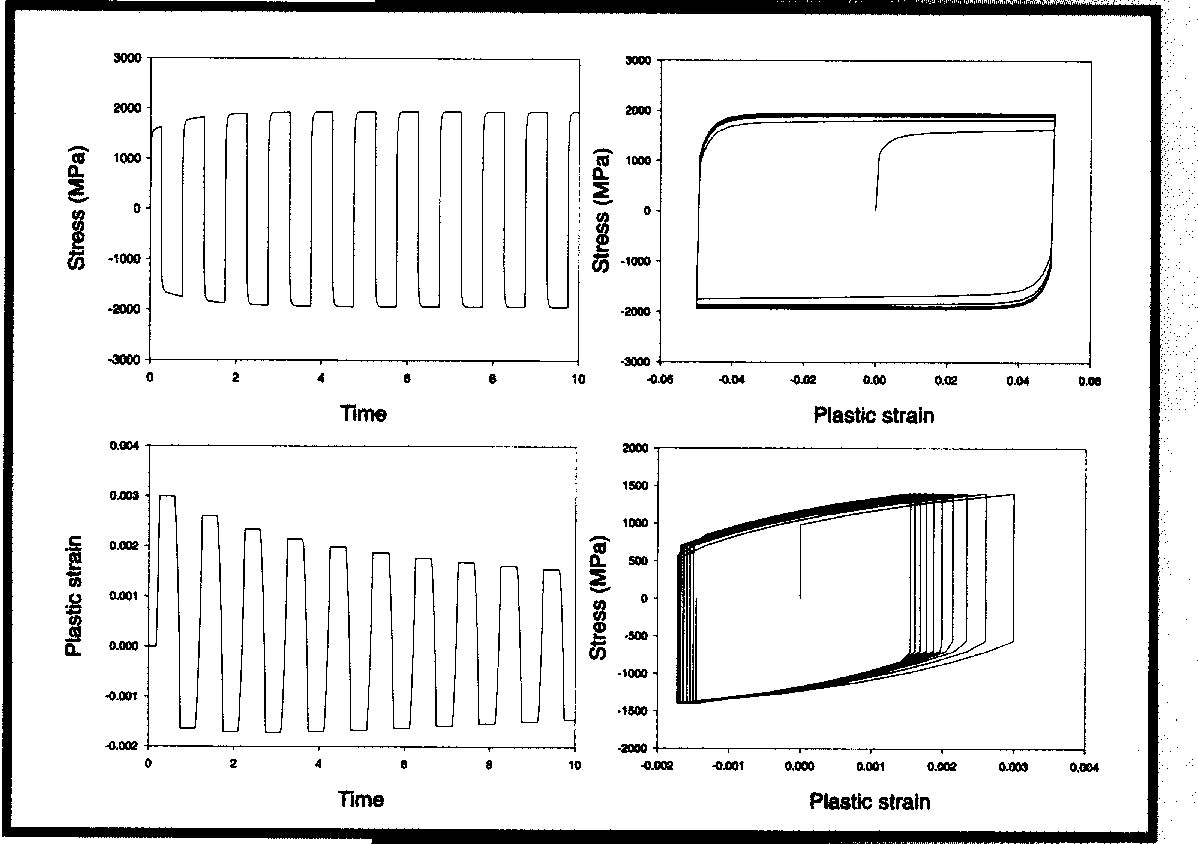
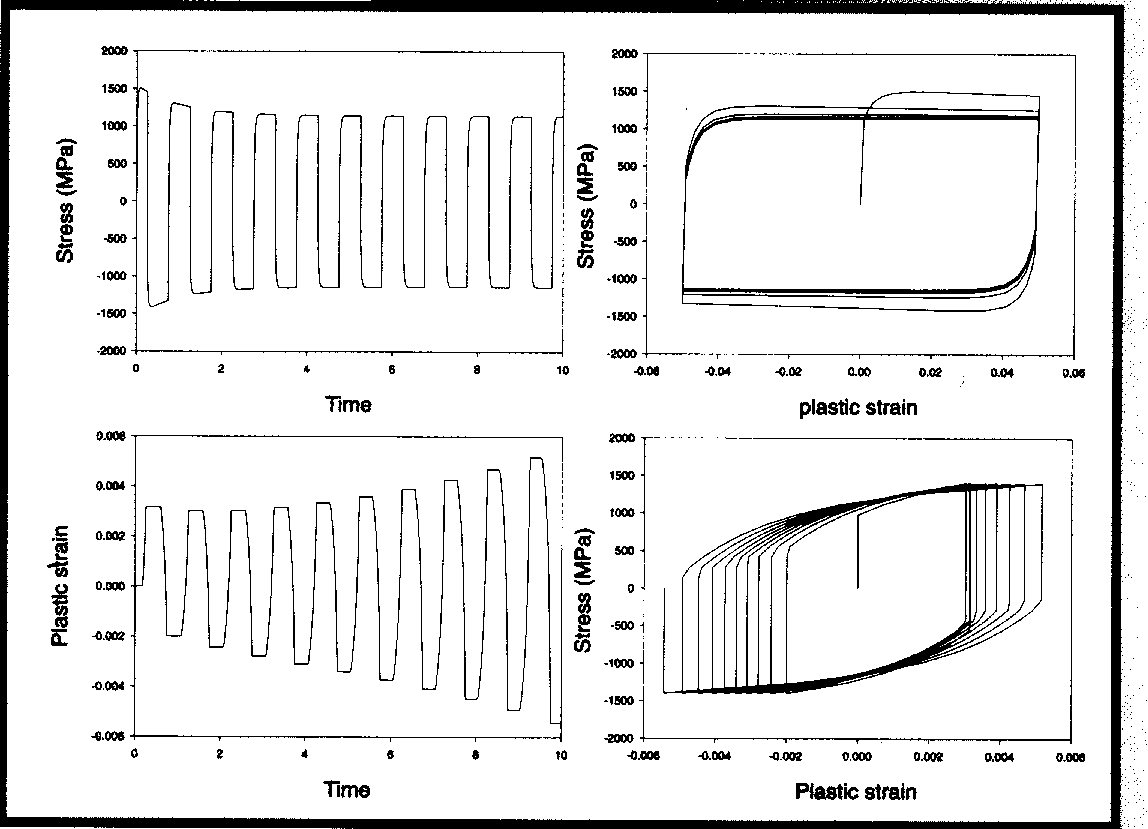
При циклическом нагружении большинство металлов и сплавов меняют свое поведение в области упрочнения с ростом числа циклов. В зависимости от материала, температуры и исходного состояния может происходить упрочнение или разупрочнение. Под циклическим разупрочнением подразумевается убывание приращения напряжений с каждым последующим циклом в случае регулируемой нагрузки, а в случае регулируемых деформаций - возрастание с каждым последующим циклом приращения деформаций. Под циклическим упрочнением подразумевается убывание приращения деформаций с каждым последующим циклом в случае регулируемой нагрузки, а в случае регулируемых деформаций - возрастание с каждым последующим циклом приращения напряжений. Проще говоря, если при повторных нагружениях напряжения текучести возрастают, то имеет место циклическое упрочнение (рис. 12). Если при повторных нагружениях напряжения текучести убывают, то имеет место циклическое разупрочнение (рис. 13). В программе ANSYS 5.6 предусмотрена возможность моделировать как циклическое упрочнение, так и разупрочнение. Сочетание моделей кинематического и изотропного упрочнения охватывает весьма широкий круг существующих потребностей (табл. 2).

Уравнение состояния Друкера-Прагера применимо для гранулированного (с трением) материала типа грунта, горных пород и бетона, построено на приближении к закону Мора-Кулона в виде конической поверхности. Пластическое поведение характерно для сжимаемого материала. Это значит, что пластическое состояние может быть вызвано действием гидростатического давления, тогда как уравнения состояния материалов, построенные исключительно на энергетическом критерии Мизеса, не учитывают всестороннего давления.

Программа ANSYS содержит весьма широкие возможности для моделирования нелинейного поведения материалов. Стоит только объединить их с другими преимуществами программы ANSYS: эффективными решателями, средствами создания контактов типа «поверхность-поверхность», возможностями преобразования сетки конечных элементов, модулями решения задач мультифизики - и набор программных средств компании ANSYS проявит себя как исключительно многосторонний и мощный пакет.

Вторая часть этой статьи, которая будет опубликована в следующем выпуске, завершит рассмотрение сложного поведения материалов подробным изложением нелинейных, неупругих, зависящих от скорости деформаций реологических моделей, включая ползучесть.

Рис. 12

Рис. 13

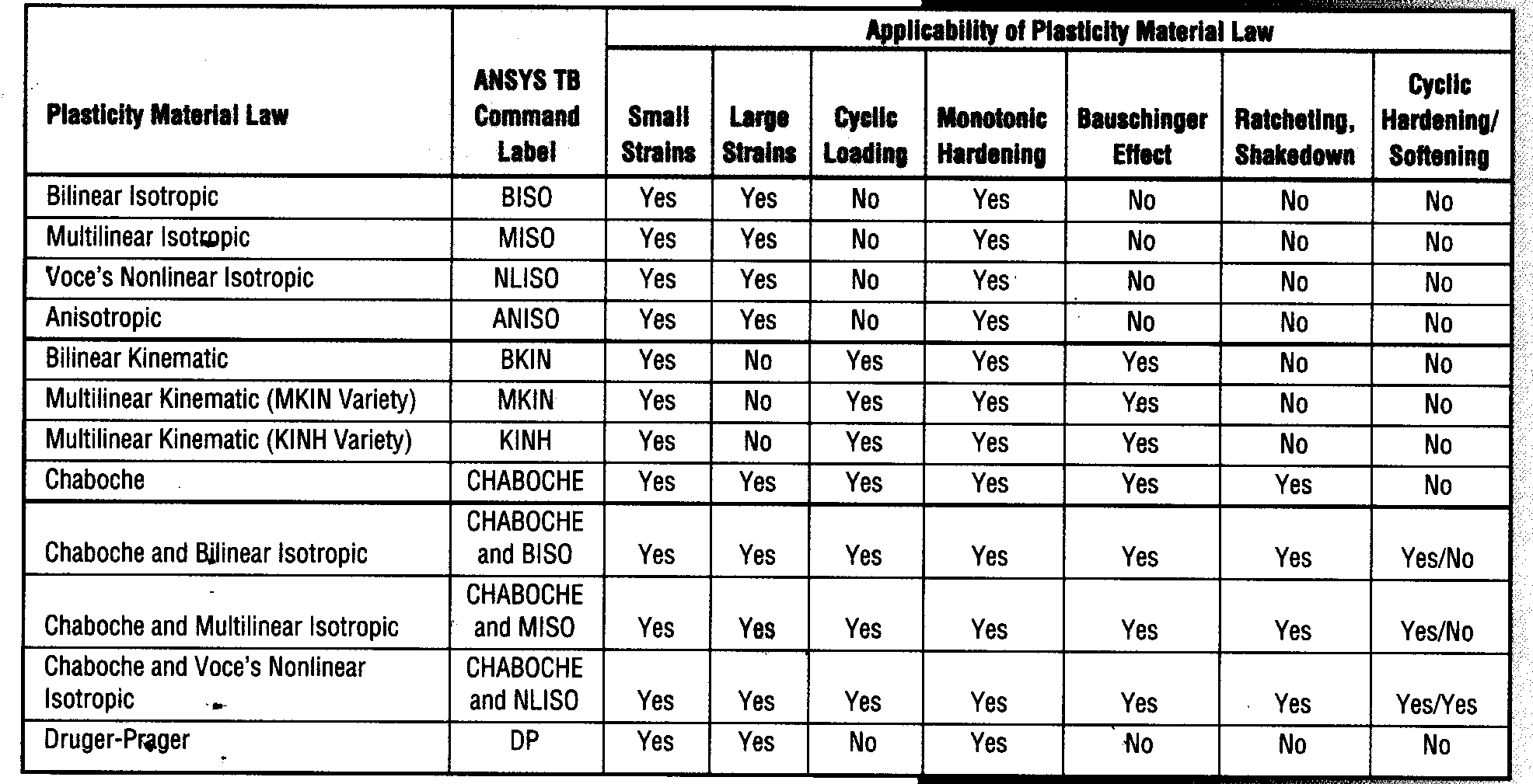
Таблица 2. Применимость моделей

пластического поведения

---