Politechnika Białostocka
Wydział Budownictwa i Inżynierii Środowiska
Sprawozdanie z zajęć laboratoryjnych
z wytrzymałości materiałów
Numer ćwiczenia: 7
Temat ćwiczenia: Badanie prętów prostych na wyboczenie.
...................................................................................................
(imię i nazwisko studenta)
rodzaj studiów:
kierunek:
semestr:
grupa:
prowadzący ćwiczenia:
..........................................
(data wykonania ćwiczenia)
Cel ćwiczenia:
Celem ćwiczenia jest doświadczalne wyznaczenie wartości siły krytycznej dla pręta wykonanego z danego tworzywa i porównanie jej z siłą krytyczną obliczoną ze wzoru Eulera.
Podstawy teoretyczne z uwzględnieniem norm (PN)
Przy wyprowadzeniu wzoru Eulera na siłę krytyczną zakłada się, że pręt jest prostoliniowy, a siły ściskające przyłożone do jego końców działają wzdłuż osi. Do wywołania wyboczenia pręta, przy założeniu idealnej jego osiowości, konieczna jest nie tylko dostatecznie duża siła, ale i nagły impuls siły poprzecznej dla wywołania wstępnej, nieskończenie małej krzywizny. W przeciwnym przypadku siła mogłaby wzrastać nie wywołując wyboczenia sprężystego aż do chwili, gdy w którymś z przekrojów poprzecznych pręta powstałby przegub plastyczny, przekształcający pręt w układ kinematyczny. W układach rzeczywistych zawsze istnieje pewna nie prostoliniowość pręta lub nie osiowość przyłożenia siły i dlatego do wywołania wyboczenia sprężystego nie są konieczne poprzeczne impulsy.
Siłą krytyczną nazywamy taką jej wartość, przy której znika prawdopodobieństwo zachowania przez pręt początkowego prostoliniowego kształtu.
Na wartość siły krytycznej pręta mają wpływ:
1) sposób jego podparcia i długość,
2) geometria przekroju,
3) moduł Younga, tj. własności mech. tworzywa.
Pręt wyboczy się z płaszczyzny max smukłości. Może podlegać wyboczeniu sprężystemu i niesprężystemu w zależności od wartości smukłości.
gdzie:
lw = μ l - zredukowana długość wyboczenia,
μ - współczynnik redukcji długości wyboczeniowej l, zależne od warunków brzegowych pręta.
Promień bezwładności
Jmin - minimalny osiowy moment bezwładności przekroju,
A - pole pow. przekroju poprzecznego.
Przypadki wyboczenia sprężystego i niesprężystego rozpatruje się oddzielnie. Wzór na siłę krytyczną wyboczenia sprężystego prętów prostych o stałym przekroju podał Euler. Bierzemy pod uwagę uproszczone równanie różniczkowe osi odkształconego pręta
dla przypadku z rysunku mamy:
podstawiając otrzymujemy :
gdzie
Jak wiadomo, równanie charakterystyczne posiada oba pierwiastki urojone. W związku z tym całka równlania ma postać:
z warunków brzegowych:
znajdujemy C2 = 0 z pierwszego i z drugiego, ponieważ C1 ≠ 0
przy
stąd
oraz ogólny wzór na siłę krytyczną
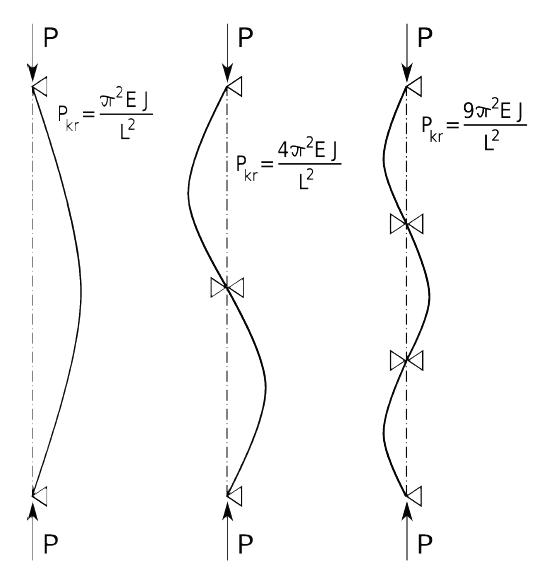
Ostatecznie, gdy
siła krytyczna jest równa:
gdy
siła krytyczna jest równa:
oraz gdy
siła krytyczna jest równa:
Ze względów bezpieczeństwa, najważniejsza jest najmniejsza wartość siły krytycznej, ale wszystkie przedstawione rozwiązania mają znaczenie praktyczne. Wartość
odpowiada sinusoidalnemu ugięciu pręta z jedna półfalą zgodnie ze wzorem
Aby pręt przyjął kształt sinusoidy o dwóch półfalach należy go unieruchomić w środku długości, a siła wywołująca wyboczenie będzie wówczas równa
Unieruchomienie pręta w trzech miejscach spowoduje jego wygięcie w kształcie sinusoidy o trzech półfalach, a potrzebna do tego sił musi być nie mniejsza niż
Mnożnik
w w/w wzorach
jest równy liczbie półfal wygiętego pręta, natomiast
określa liczbę podpór pośrednich potrzebnych do zablokowania pręta.
Pręt poddany wyboczeniu ma tendencje do wychylania się w płaszczyźnie najmniejszej sztywności, której odpowiada najmniejszy moment bezwładności. Naprężenia spowodowane siła krytyczna określa się naprężeniami krytycznymi:
gdzie:
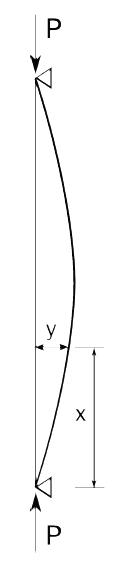
jest smukłością pręta odpowiednio w kierunku
x lub y.
- dłg. wyboczeniowa
Schemat i zasada działania urządzenia pomiarowego
Próbka-pręt (1) o przekroju prostokątnym i długości l jest osadzony w podporze nieruchomej (2) i ruchomej (3) poruszającej się w prowadnicy (4). Pomiaru wychylenia poprzecznego pręta dokonuje się za pomocą czujnika zegarowego (5) i szalki (7) i ciężarków (8) obciążają pręt przez przegub kulisty (6).
Przebieg ćwiczenia
Próba wyboczenia wykonywana jest na prostym pręcie o przekroju prostokątnym 50 × 6mm i długości L = 800mm. Pręt mocujemy w maszynie wytrzymałościowej początkowo bez podpór pośrednich, mierzymy wielkość siły krytycznej. Badanie powtarzamy po prowadzeniu w środku długości pręta jednej podpory pośredniej.
Czynności przed rozp. badania
- zmierzyć wymiary pręta d,
-ustalić analitycznie wielkość siły krytycznej, dla pręta ściskanego bez podpór pośrednich,
-ustalić analitycznie wielkość siły krytycznej, dla pręta ściskanego z jedna podpora pośrednią,
-właściwie zamocować pręt w maszynie wytrzymałościowej.
4.2 Czynności podczas badania
- Podczas próby należy jedynie odpowiednio odczytać wielkości sił krytycznych w obu schematach podparcia pręta.
5. Opracowanie wyników
Cechy geometryczne przekroju:
-długość pręta:
L = 800 [mm]
-wymiary przekroju poprzecznego:
b x h = 6 x 50
-pole przekróju poprzecznego:
A = 300 [mm2]
-moment bezwładności względem osi x:
[mm4]
-moment bezwładności względem osi y:
[mm4]
-promień bezwładności względem osi y:
[mm]
-promień bezwładności względem osi x:
[mm]
Ustalenie siły krytycznej osiowo ściskanego pręta - bez podpór pośrednich:
-długość wyboczeniowa pręta dla
:
-smukłość pręta względem osi x:
-smukłość pręta względem osi y:
-siła krytyczna:
-naprężenia krytyczne
Ustalenie siły krytycznej osiowo ściskanego pręta - z jedną podporą pośrednią
-długość wyboczeniowa pręta dla
:
-smukłość pręta względem osi x:
-smukłość pręta względem osi y:
-siła krytyczna:
-naprężenia krytyczne
Obliczenie ilości podpór - n , aby wyboczenie nastąpiło w drugim kierunku
Założenia: Warunek: Obliczenia:
, stąd otrzymujemy n=10
Ustalenie siły krytycznej osiowo ściskanego pręta - z 10 podporami pośrednimi:
-długość wyboczeniowa pręta dla
:
-smukłość pręta względem osi x:
-smukłość pręta względem osi y:
-siła krytyczna:
-naprężenia krytyczne
Wnioski
-wyboczenie może pojawić się w elementach konstrukcyjnych takich jak słupy,belki,podpory
-siła Pkr1 oraz siła Pkr2 obliczone analitycznie są w przybliżeniu równe siłom osiągniętym doświadczalnie, a naprężenia krytyczne są mniejsze niż wytrzymałość na ściskanie stali
-aby wyboczenie pręta nastąpiło w drugim kierunku należy użyć 10 podpór pośrednich, uzyskane wówczas naprężenia są nadal mniejsze niż wytrzymałość na ściskanie stali
Wyszukiwarka
Podobne podstrony:
TABELKI DO 4 SPRAWOZDANIA, Budownictwo PB, 5 semestr, Mechanika Gruntów, laborki
strona tytulowa do sprawozdan, AK sem II (PB), szkoła
sprawozdanie betony Dawida, studia budownictwo PB PWSZ, SEM III, technologia betonu
Sprawozdanie z laborek diagram Sn i Pb
2 definicje i sprawozdawczośćid 19489 ppt
PROCES PLANOWANIA BADANIA SPRAWOZDAN FINANSOWYC H
W 11 Sprawozdania
Wymogi, cechy i zadania sprawozdawczośći finansowej
Analiza sprawozdan finansowych w BGZ SA
W3 Sprawozdawczosc
1 Sprawozdanie techniczne
Karta sprawozdania cw 10
eksploracja lab03, Lista sprawozdaniowych bazy danych
2 sprawozdanie szczawianyid 208 Nieznany (2)
Fragmenty przykładowych sprawozdań
Lab 6 PMI Hartownosc Sprawozdan Nieznany
PB BO W1
więcej podobnych podstron