Imię i nazwisko:	Ćw. O3 Wyznaczenie stałej siatki dyfrakcyjnej.
Kierunek i rok:	Ocena z kolokwium: ………………….. …………………... Data/podpis	Ocena ze sprawozdania: …………………... …………………... Data/podpis	Ocena końcowa: …………………... …………………... Data/podpis
Nazwisko prowadzącego zajęcia:

Cel doświadczenia.

Wyznaczenie stałej siatki dyfrakcyjnej.

Przebieg doświadczenia.

1. Dla 2 siatek dyfrakcyjnych wyznaczyć stałą siatki.

2. W tym celu włączamy laser ustawiamy przed nią siatkę najpierw pierwsza potem drugą.

3. Następnie obserwujemy na ekranie wzmocnienia interferencji promienia lasera.

Teoria.

Dyfrakcja to zjawisko fizyczne zmiany kierunku rozchodzenia się fali na krawędziach przeszkód oraz w ich pobliżu. Zjawisko zachodzi dla wszystkich wielkości przeszkód ale wyraźnie jest obserwowane dla przeszkód o rozmiarach porównywalnych z długością fali.

Interferencja to zjawisko nakładania się fal prowadzące do zwiększania lub zmniejszania amplitudy fali wypadkowej. Interferencja zachodzi dla wszystkich rodzajów fal, we wszystkich ośrodkach, w których mogą rozchodzić się dane fale. W ośrodkach nieliniowych oprócz interferencji zachodzą też inne zjawiska wywołane nakładaniem się fal, w ośrodkach liniowych fale o jednakowej częstotliwości ulegając interferencji spełniają zasadę superpozycji.

Laser półprzewodnikowy czyli dioda laserowa działa podobnie jak diody świecące LED (skrót od angielskiego light emitting diode). LED zamieniają energię elektryczną na światło widzialne lub promieniowanie podczerwone. Źródłem światła jest złącze półprzewodnikowe n-p. Światło powstaje w wyniku tego, że elektrony w paśmie przewodnictwa są pobudzane do rekombinacji z dziurami w paśmie walencyjnym. Gdy zachodzi to zjawisko, elektrony oddają energię odpowiadającą przerwie wzbronionej i następuje świecenie. Do tych celów przydatne są takie materiały jak arsenek galu lub azotek galu, a obecnie częściej cienkie warstwy półprzewodników. Diody LED wysyłają światło niespójne i nie do końca monochromatyczne. Aby powstał laser należy tak uformować układ aby powstał rezonator optyczny. Gdy do złącza będą wstrzykiwane duże ładunki to może w nim powstać proces laserowy i w wyniku wymuszonych przejść z pasma przewodnictwa do walencyjnego generuje się spójna wiązka światła.

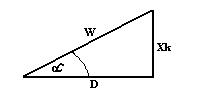
Gdy porównamy ze sobą sinusy otrzymamy wzór na stała siatki dyfrakcyjnej.

Obliczenia.

Siatka dyfrakcyjna nr 1.

L.p.	D [m]	2x1 [m]	2x2 [m]	x1 [m]	x2 [m]
1	0,050	0,021	0,040	0,0105	0,020
2	0,100	0,038	0,080	0,0190	0,040
3	0,135	0,053	0,113	0,0265	0,057
4	0,170	0,070	0,150	0,0350	0,075
5	0,225	0,088	0,165	0,0440	0,083

Obliczam stałą siatki.

L.p.
1	3,26	3,61
2	3,59	3,61
3	3,48	3,47
4	3,32	3,20
5	3,49	3,89
Suma	1,71	1,79

Stałą obliczam z wzoru
dla prążków pierwszego rządu
i dla prążków drugiego rzędu
. Gdzie
i 2
.

Obliczam wartości średnie d dla siatki z wzoru
.

Obliczam odchylenie standardowe średniej arytmetycznej z wzoru

Obliczam przedział ufności wartości d dla poziomu ufności
oraz
, z wzoru

Przy czym:

Dla

Dla

Obliczam liczbę rys na milimetr z wzoru

Siatka dyfrakcyjna nr 2.

L.p.	D [m]	2x1 [m]	2x2 [m]	x1 [m]	x2 [m]
1	0,13	0,04	0,07	0,02	0,04
2	0,18	0,04	0,10	0,02	0,05
3	0,26	0,07	0,14	0,03	0,07
4	0,30	0,08	0,14	0,04	0,07
5	0,36	0,09	0,19	0,05	0,09

Obliczam stałą siatki.

L.p.
1	5,02	5,15
2	5,78	5,25
3	5,32	5,30
4	5,40	5,90
5	5,40	5,38
Suma	2,69	2,70

Stałą obliczam z wzoru
dla prążków pierwszego rządu
i dla prążków drugiego rzędu
. Gdzie
i 2
.

Obliczam wartości średnie d dla siatki z wzoru
.

Obliczam odchylenie standardowe średniej arytmetycznej z wzoru

Obliczam przedział ufności wartości d dla poziomu ufności
oraz
, z wzoru

Przy czym:

Dla

Dla

Obliczam liczbę rys na milimetr z wzoru

Wnioski.

Celem doświadczenia było wyznaczenie stałej siatki. Otrzymałem następujące wyniki:

Dla siatki nr 1.

Dla siatki nr 2.

Są to wartości średnie, jednak na podstawie tabel z wartościami poszczególnych wielkości d dla różnych odległości siatki od ekranu można stwierdzić, że są do siebie zbliżone i nieznacznie się różni. Poza tym otrzymane wartości są rzędu
. Na tej podstawie można stwierdzić, że doświadczenie zostało przeprowadzone prawidłowo a otrzymane wielkości są prawdziwe.

Ponad to miałem wyznaczyć przedział ufności wartości d dla poziomu ufności
oraz
, oraz liczbę rys na milimetr N.

Dla siatki nr 1.

Dla siatki nr 2.

d- odległość miedzy środkami sąsiednich szczelin czyli tzw. stała siatki dyfrakcyjnej.

- dł. Fali.

k- nr Prążka oddalonego o prążka zerowego.

- jest to różnica odległości dróg fal jakie mają do przebycia miedzy siatką a ekranem.

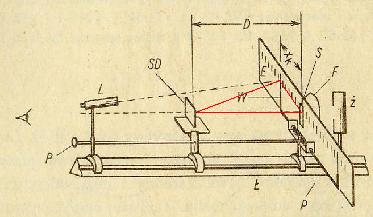
Zatem na podstawi rysunku obok można wyznaczyć następujący wzór:

Ż- źródło światła.

E- ekran

SD- siatka dyfrakcyjna.

D- odległość siatki od ekranu.

- odległość k- tego prążka od prążka zerowego.

Z Obu rysunków można zauważyć że:

---