WYKŁAD NR 5

Aby lepiej zrozumieć i poznać metodę optymalizacji (opracowaną ok. 60 lat temu przez Bellmana) - programowania dynamicznego - przedstawioną poniżej przeanalizujmy następujący przykład.

PRZYKŁAD.1.

Zasoby kapitałowe w postaci 7 jednostek, możemy ulokować w 3 interesach. Przyjmujemy opcje inwestycji tak jak w tabeli1. Tabela ta przedstawia spodziewane zyski w jednym z trzech interesów przy zainwestowaniu określonych nakładów inwestycyjnych. Jeżeli więc zainwestujemy zero jednostek - zysk będzie zerowy dla każdej z inwestycji, jeżeli natomiast jedną jednostkę kapitałową umieścimy w I interesie uzyskamy 2 jednostki, w interesie II - 3 jednostki, w III interesie - 1 jednostkę, itd. Symbol „- ” oznacza, że nie ma fizycznych możliwości zainwestowania określonej sumy w danym interesie.

Mając dane z tabeli pierwszej, tworzymy macierz zysków (rys.1.) biorąc pod uwagę inwestycję I i II

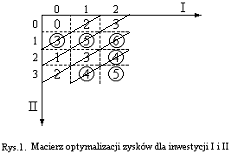
Liczby ponad osiami to jednostki inwestycyjne w określonej inwestycji. Oś pozioma odnosi się do interesu I, pionowa do II. Poszczególne wyrazy macierzy tworzy się sumując zyski. Na przykład wkładając 1 jednostkę inwestycyjną w inwestycję I i 2 jednostki w inwestycję II zysk wynosi 2+1=3 jednostki, itd. Wartości zakreślone to optima zysków, które wykorzystane zostaną do tworzenia następnej macierzy (rys.2) obejmującej wszystkie trzy inwestycje. Po przekątnych znajdują się wartości zysków uzyskanych z inwestycji stałej liczby jednostek zainwestowanych, w zależności od interesu. Patrząc na poszczególne przekątne z łatwością można określić optymalny zysk przy określonych inwestycjach.

Nowa macierz wygląda następująco:

Podobnie jak w poprzednim przypadku, poszczególne elementy macierzy tworzone są przez sumowanie zysków wynikających z zainwestowania określonych nakładów w poszczególnych przedsięwzięciach. Z tą tylko różnicą, że zysk dotyczący inwestycji I i II to optima z macierzy z rys.1.

Przeprowadzone analizy wykazały, że maksymalny zysk jaki można uzyskać z zainwestowania 7 jednostek inwestycyjnych to 11. Wynik taki uzyskujemy umieszczając 4 jednostki w przedsięwzięciu III , oraz 3 jednostki w I i II traktowanych tu łącznie. Z macierzy na rys.1. odczytujemy, że maksymalny zysk z zainstalowania 3 jednostek kapitałowych w I

i II łącznie osiąga się gdy 1 jednostkę ulokujemy w przedsięwzięciu II i 2 jednostki w I.

PRZYKŁAD.2.

W projektowanym układzie zasilania GPZ zasila promieniowo trzy ST SN/0,4 kV. Każda z projektowanych ST ma być trójtransformatorowa. Minimalny przekrój kabli zasilających ST z GPZ wynosi 95mm². Obciążenia stacji, bez kompensacji mocy biernej, oraz odległości ST od GPZ są następujące:

• ST1:
  = 2,30+j 1,60 MVA;
  =0.40 km;

• ST2:
  = 3,38+j 2,07 MVA;
  =0,15 km;

• ST3:
  = 2,54+ j2,37 MVA;
  =0 km;

= 8,22 +j 6,04 MVA

Z wielkości
oblicza się kąt
, a następnie
.

Współczynnik mocy narzucony przez dostawcę energii
=0,913, (
). Należy skompensować moc bierną o wartość
Mvar.

Założono kompensację regulowanymi bateriami kondensatorów, które moż­na zainstalować jedynie w ST po stronie 0,4 kV. Założono q = 360 kvar, więc
oraz, że po kompensacji współczynnik mocy w żadnym z elementów sieci nie może być większy niż 0,95.

Rys 3. Wykres obciążenia transformatorów stacji nr 1

Z wykresu na rys.3. wynika że:

• bez kompensacji
  [kVA]

• z kompensacją 360[kvar]
  [kVA]

• ale z kompensacją 2x360[kvar]
  [kVA]

Dla uproszczenia pominięta została możliwość przeciążenia transformatora.

Rozwiązanie zadania w pierwszej kolejności polega na znalezieniu zależności
,między obciążeniem poszczególnych ST kabli 15 kV, a mocą bierną kompen­sowaną

Rys 4. Wykresy kosztów rocznych K_r: linia ciągła - transformatory; linia przerywana - kable 15 kV. 1 km; linia kreska-kropka

Tablica 4. Funkcje zmian kosztów rocznych trzech stacji transformatorowych w przykładzie2.

Z
0	0	0	0
1	280	380	380
2	20	70	570
3	-	-	760
4	-	-	990

w tych ST. Przykładowo na rys.3. przedstawiono zależność między ob­ciążeniem ST1 a mocą bierna kompensowaną w tej stacji. Na rysunku 4. przedstawiono funkcje kosztów poszczególnych elementów układu. Na podstawie zależności
i funkcji obliczono funkcje zmiany kosztów
. Wartości tych funkcji zestawiono w tabl.2. Należy znaleźć minimum funkcji

przy spełnieniu warunków

Oblicza się elementy macierzy A¹. Elementy w zerowym wierszu i w zerowej kolumnie odczytuje się wprost z tabl. 2. Pozostałe elementy oblicza się, np.

Na podstawie A¹ oblicza się
. W tym celu można w macierzy A¹ wrysować przekątne łączące elementy, dla których i+j = const, a następnie wybrać najmniejszą wartość na każdej z tych przekątnych:

Następnie oblicza się elementy macierzy A². Na przykład

Na podstawie A² oblicza się









. Stąd minimum
spełniające warunek
jest równe
. A więc i = z₃ = 3, j = ^C(2) = 4.

Dla z₁ + z₂ = 4.
, stąd i = z₂ = 2, j = C⁽¹⁾ = z₁ = 2.

Tak więc minimum kosztów rocznych otrzymano przy
kvar;
kvar;
kvar.

Algorytm najkrótszej ścieżki w grafie zorientowanym służy do znajdowania najkrótszego łańcucha. Algorytm ten jest oparty na następujących założeniach:

• jest spełniona zasada optymalności, a więc kryterium optymalności jest addytywne,

• graf jest skierowany,

• węzły grafu są tak ponumerowane, że węzeł następnik ma zawsze większy numer od numeru węzła poprzednika, czyli przejścia do danego węzła są możliwe tylko z węzłów o mniejszym numerze.

Oznaczmy przez:

zbiór węzłów poprzedników danego węzła
,

- długość (koszt) łuku
(jeżeli graf nie zawiera łuku
należy przyjąć
).

Algorytm:

Oblicza się
, przy czym
,
(*)

Ze wzoru (*) oblicza się kolejno
przy czym n jest liczbą węzłów grafu. Wartość
jest długością najkrótszego łańcucha w grafie. Łuki składające się na ten łańcuch reprezentują warianty rozwoju stacji. Aby te łuki znaleźć dokonuje się przeglądu obliczeń od końca.

Metoda algorytmu najkrótszej ścieżki w grafie zorientowanym będzie bardziej jasny po wcześniej analizie następującego przypadku;

PRZYKŁAD.3.

Mamy dobrać silnik do napędzania danego urządzenia, poprzez linie kablową. Możemy więc to zrobić wykorzystując trzy możliwości: 1) dobrać silnik synchroniczny, droższy ale nie wymagający stosowania kompensacji mocy bierne, gdyż jest on sam dla siebie źródłem mocy biernej, 2) dobrać silnik asynchroniczny, tańszy ale w tym przypadku kompensacja realizowana jest grupowo, 3) przypadek jak poprzednio z tą jednak różnicą iż stosujemy kompensacje indywidualną. Powyższe rozwiązania zamieszczone są na rys.5.

Na rys.6 znajduje się graf skierowany będący równoważna interpretacją omawianego przypadku.

Rys.6. a)Graf możliwych rozwiązań, b) graf zorientowany z cechami węzłów

Zgodnie z założeniami graf jest skierowany (zorientowany) a węzły grafu są tak ponumerowane, że każdy węzeł następny grafu ma numer zawsze większy niż poprzednik. Tak więc z 1 do 4 możemy dojść pokonując kolejno węzły 1-2-3-4, 1-3-4, oraz 1-2-4 co odpowiada zaproponowanym wcześniej rozwiązaniom. Poszczególnym odcinkom grafu przypisane są koszty jakie wiążą się z realizacją poszczególnych „etapów” rozwiązań. Do każdego węzła (z wyjątkiem węzła 1) przypisana jest również cecha. Cechą w naszym przypadku jest minimalna suma kosztów „drogi” z węzła poprzedniego do węzła następnego. I tak cechą węzła 2 jest koszt równy 40, do węzła 3 możemy dotrzeć dwoma drogami więc jego cechą będzie minimum kosztów drogi 1-3 i drogi 1-2-3. Analogicznie postępujemy w przypadku pozostałych węzłów. Ważne przy wyliczaniu cech węzła następnego jest to, że mając wyliczoną cechę węzła wcześniejszego do sumy nie patrzymy na koszty „drogi” do węzła wcześniejszego tylko na jego cechę. Poniżej zaprezentowano sposób liczenia cech:

C₂ =

C₃ =

Z realizacji powyższego toku myślowego otrzymujemy minimum kosztów i optymalne rozwiązanie dla zadania.

Możliwość wykorzystania metody najkrótszej ścieżki w grafie zorientowanym dla konkretnych problemów projektowych pokazany jest w przykładzie następnym.

PRZYKŁAD.4.

Na rys.7. podano graf sieci SN odlewni staliwa. Optymalizowano: napięcie znamionowe sieci SN (do wyboru 6 [kV] lub 15[kV]), ilość rozdzielni pośrednich SP średniego napięcia (do wyboru 1,2 lub 4) - co wiąże się z doborem kabli i typu pól rozdzielni SN, ilość i moc transformatorów SN/nn (trzy warianty ) oraz układ sieci SN z SP do transformatorów (promieniowy lub łańcuchowy).

Na rys.7. naniesiono grubiej „najkrótsze trasy w grafie” osobno dla napięcia sieci 6 [kV] i 15[kV].

Na rys.8. podano graf sieci zasilających wentylatory nawiewu odmrażalni rudy od GPZ-u do silników włącznie.

Optymalizowano: układy sieci SN (do wyboru promieniowy lub pierścieniowy), ilość stacji transformatorowych (trzy warianty), ilość transformatorów w stacji transformatorowej (dwa warianty) sposób kompensacji mocy biernej (do wyboru kompensacja indywidualna, grupowa, centralna lub zastosowanie silników synchronicznych). Łączna ilość możliwych wariantów układu - 40. Na rysunku grubszą linią oznaczono optymalny wariant.

Rys.7.Graf wariantów sieci ŚN odlewni staliwa.

Wnioski

Metoda umożliwia łatwe „dorabianie” nowych wariantów układu. Np. uwzględnienie nowego wariantu poszczególnych elementów układu nie wymaga powtarzania całości obliczeń.

W przypadku konieczności odrzucenia rozwiązania optymalnego ze względu na trudności w zakupie optymalnych urządzeń łatwo znaleźć optymalne rozwiązanie w nowych warunkach.

Rys.8.Graf sieci ŚN i n.n. odmrażalni rudy

5

---