Imię i nazwisko:	Ćwiczenie nr C4 Wyznaczanie κ = cp /cv dla powietrza metodą Clementa-Desormesa.
Kierunek i rok:	Ocena z kolokwium: ....................................... data ....................... podpis...........................	Ocena ze sprawozdania: ....................................... data ....................... podpis...........................	Ocena końcowa: ....................................... data ....................... podpis...........................
Nazwisko prowadzącego zajęcia:

Gaz doskonały - hipotetyczny gaz obdarzony następującymi cechami:

1. cząstki gazu są punktami materialnymi lub sztywnymi układami punktów materialnych, atomów (mających pomijalnie małą objętość własną),

2. zderzenia między cząsteczkami gazu są doskonale sprężyste,

3. między cząsteczkami nie występują oddziaływania z wyjątkiem chwil zderzeń,

4. między kolejnymi zderzeniami cząsteczki poruszają się ruchem jednostajnym prostoliniowym w dowolnych kierunkach.

Gazy rzeczywiste w wysokich temperaturach i przy niskich ciśnieniach można traktować jak gazy doskonałe. Z wszystkich rzeczywistych gazów hel jest najbliższy ideałowi gazu doskonałego.

Równanie stanu gazu doskonałego - wzór łączący trzy parametry: ciśnienie, objętość i temperaturę bezwzględną masy stałej gazu przed przemianą (p₀, V₀, T ₀) i po przemianie (p, V, T):

Równanie Clapeyrona - równanie opisujące stan gazu doskonałego, które wiąże ze sobą podstawowe parametry gazu: ciśnienie p, objętość V, temperaturę T i ilość materii (wyrażoną w molach) n:

R - uniwersalna stała gazowa:

Przemiany gazowe:

* Przemiana izotermiczna - przemiana termodynamiczna zachodząca przy stałej temperaturze ( T = const).

Prawo przemiany izotermicznej gazu doskonałego:

W izotermicznej przemianie stałej masy gazu iloczyn jego ciśnienia p i objętości V jest stały:

Możemy też powiedzieć, że ciśnienie gazu jest odwrotnie proporcjonalne do jego objętości. Wykres tej zależności nazywa się izotermą (jest nią w układzie (p,V) hiperbola):

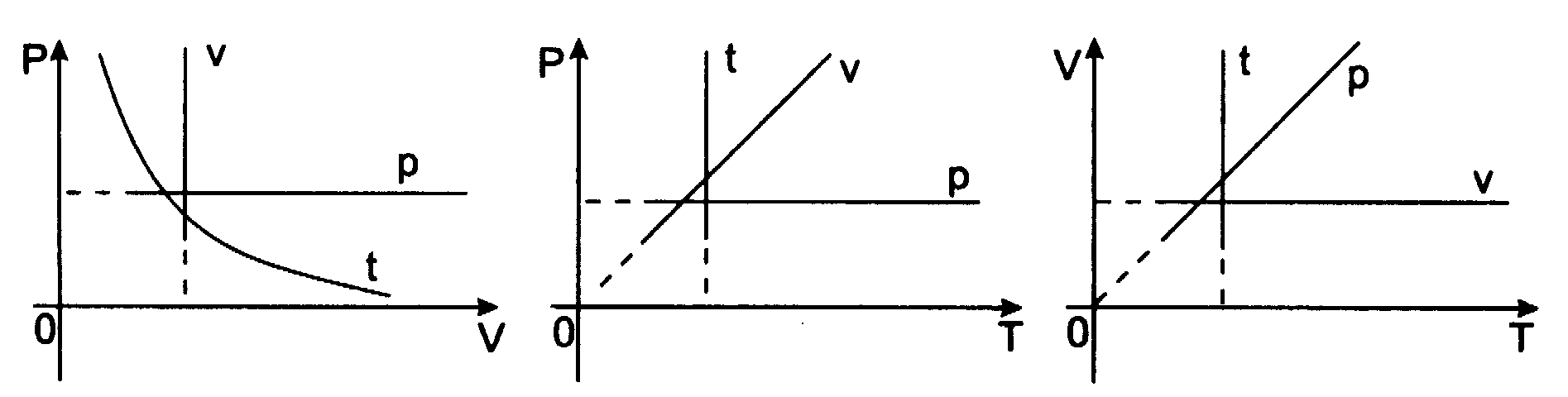
Prawo Boyle'a-Mariotte'a - prawo przemiany izotermicznej dla gazu doskonałego.

* Przemiana izochoryczna - przemiana termodynamiczna zachodząca przy stałej objętości (V = cosnt).

Prawo przemiany izochorycznej gazu doskonałego:

W izochorycznej przemianie stałej masy gazu ciśnienie jest wprost proporcjonalne do jego temperatury bezwzględnej:

Wykres tej zależności nazywa się izochorą (jest nią w układzie (p,T) linia prosta przechodząca przez początek układu):

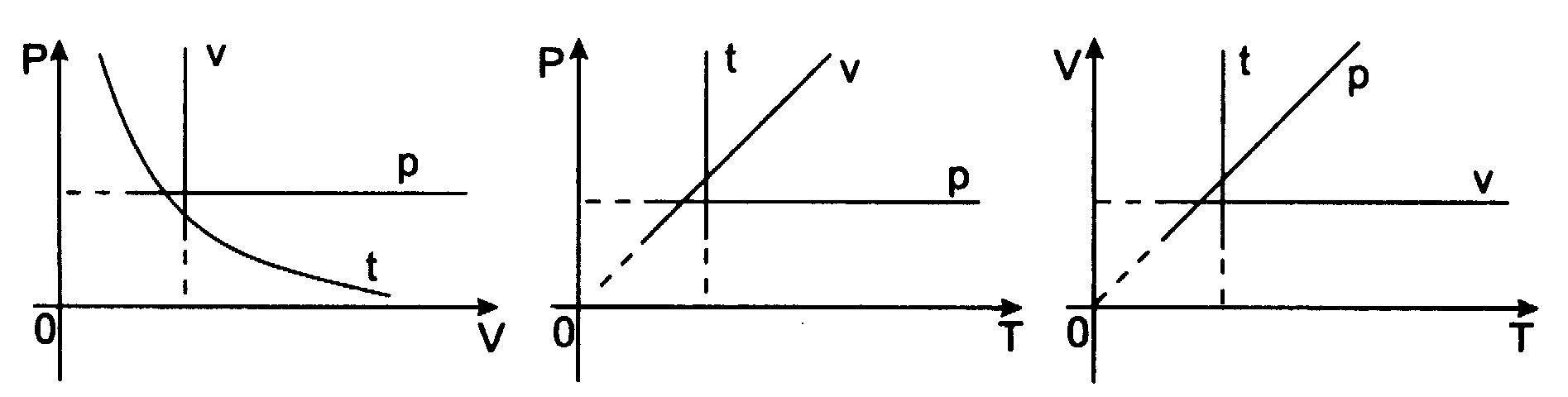
Prawo Charlesa - prawo przemiany izochorycznej dla gazu doskonałego, które w postaci zależności podanej w 1787 roku:

p - ciśnienie stałej masy gazu w temperaturze t wyrażonej w skali Celsjusza

p₀ - ciśnienie tego gazu w 0˚C

β = (273,15˚C)^-1 - współczynnik termicznej prężności gazu,

odegrało wielką rolę poznawczą. Wynikało z niej, że w temperaturze t = 273,15˚C ciśnienie gazu powinno być równe zeru. Była to pierwsza wyraźna wskazówka, że skala temperatury nie rozciąga się nieograniczenie w dół na temperatury ujemne, lecz się urywa.

* Przemiana izobaryczna - przemiana termodynamiczna zachodząca przy stałym ciśnieniu (p = const).

Prawo przemiany izobarycznej gazu doskonałego:

W izobarycznej przemianie stałej masy gazu objętość zajmowana przez gaz jest wprost proporcjonalne do jego temperatury bezwzględnej:

Wykres tej zależności nazywa się izobarą (jest nią w układzie (V,T) linia prosta przechodząca przez początek układu):

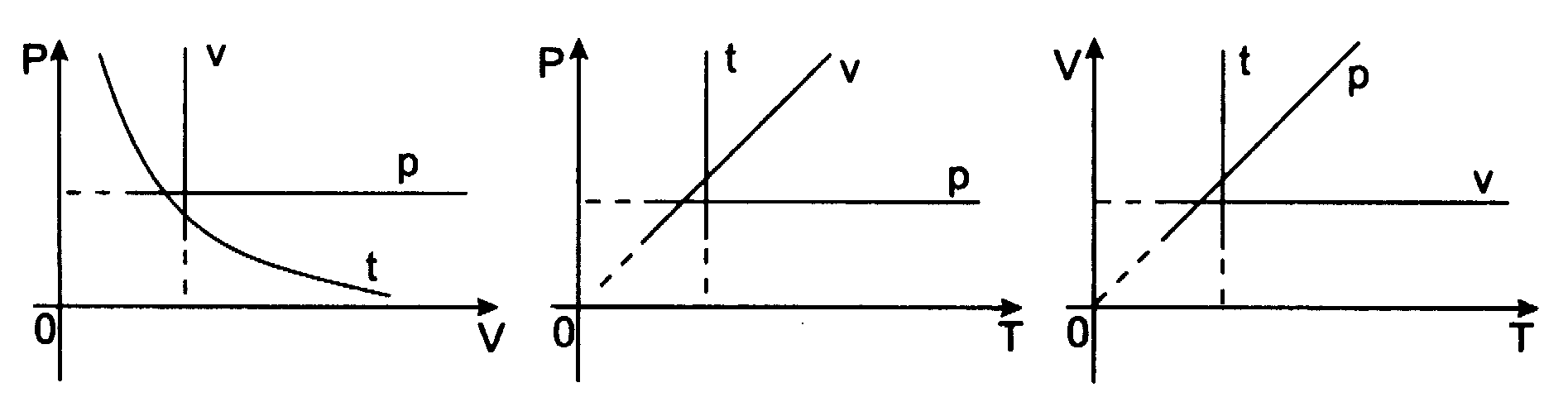
Prawo Gay-Lussaca - prawo przemiany izobarycznej dla gazu doskonałego, które można także zapisać w postaci podanej w 1802 roku:

V - objętość gazu w temperaturze t wyrażonej w skali Celsjusza

V₀ - objętość tego gazu w 0˚C

α = (273,15˚C)^-1 - współczynnik rozszerzalności objętościowej gazu.

* Przemiana adiabatyczna - przemiana termodynamiczna, która przebiega bez przepływu ciepła (Q = 0) i materii (m = const) między układem a otoczeniem.

Równanie przemiany adiabatycznej (Równanie Poissona):

Równanie opisujące zależność między objętością V gazu doskonałego, a jego ciśnieniem p w

przemianie adiabatycznej:

κ - jest stosunkiem ciepła molowego gazu pod stałym ciśnieniem c_p do ciepła molowego gazu przy stałej objętości c_v :

• dla gazów cząsteczkach jednoatomowych c = 5/3

• dla gazów o cząsteczkach dwuatomowych κ = 7/5

• dla gazów o cząsteczkach wieloatomowych κ = 4/3.

Równanie Poissona można, po skorzystaniu z równania Clapeyrona, zapisać w równoważnej postaci:

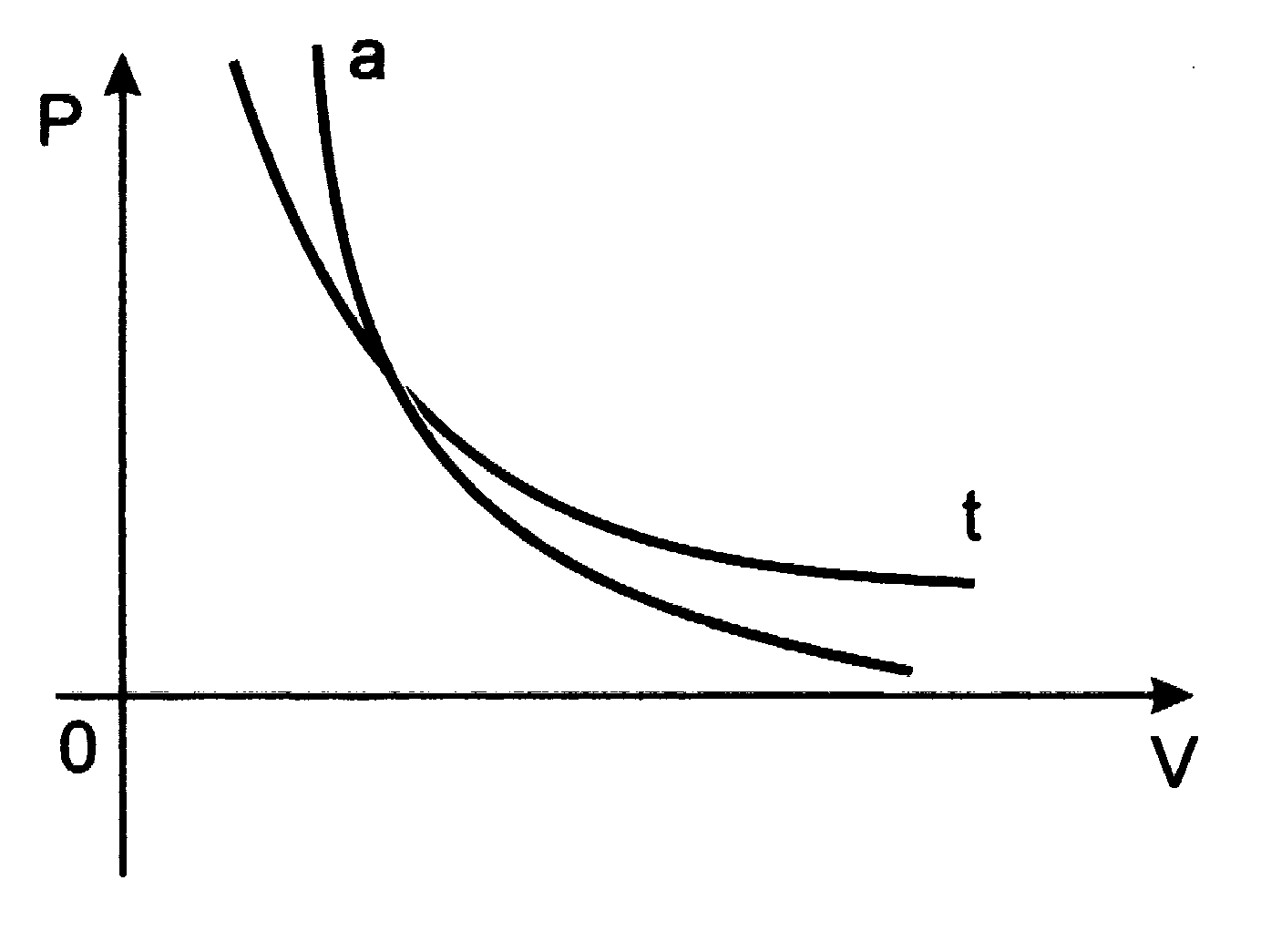
Wykresem przemiany adiabatycznej w układzie (p,V) jest adiabata:

Podstawowy wzór kinetycznej teorii gazów - wzór na ciśnienie gazu p wyprowadzony dla modelu gazu doskonałego:

V - objętość naczynia, w którym znajduje się N cząsteczek gazu,

E_Kśr - średnia energia kinetyczna cząstek (ruchu postępowego). Średnia energia kinetyczna gazu doskonałego E_Kśr jest proporcjonalna do temperatury gazu i zależy od liczby stopni swobody cząsteczki:

Wzór na ciśnienie możemy zapisać w postaci:

ρ - gęstość gazu,

v_śr² - średnia prędkość kwadratowa ruchu postępowego cząstek gazu, wyrażająca się wzorem:

m - masa cząsteczki gazu.

Ciepło (cieplny przepływ energii) Q - ta część energii wewnętrznej ∆U, którą ciało o temperaturze wyższej przekazuje ciału o temperaturze niższej bez wykonywania pracy W

Q = ∆U, gdy W = 0.

Jednostką ciepła jest kaloria, cal - pozaukładowa jednostka energii używana przy określaniu ilości ciepła, równa ilości ciepła, jakiej potrzeba do ogrzania 1g czystej wody o 1˚C. 1cal = 4,1868J.

Ciepło właściwe substancji c - stosunek ilości ciepła Q pobranego przez ciało do iloczynu masy m substancji i przyrostu jego temperatury ∆T wywołanego pobraniem tego ciepła:

Jednostką ciepła właściwego jest dżul na kilogram i kelwin:

.

Jest to ciepło właściwe ciała o masie 1 kg, którego temperatura wzrasta o 1 K po pobraniu przez nie ciepła w ilości 1 J.

Ciepło molowe c_m - stosunek ilości ciepła Q pobranego przez ciało do iloczynu liczności materii (wyrażonej przez liczbę moli) n ciała i przyrostu temperatury ∆T wywołanego jej pobraniem:

Ciepłem molowym posługuje się głównie w przypadku gazów. Ponieważ gazy charakteryzują się dużą ściśliwością istotny jest sposób przepływu ciepła (ciepło molowe zależy od przemiany termodynamicznej). Z tego względu posługujemy się ciepłami molowymi:

• ciepło molowe przy stałej objętości (dla przemiany izochorycznej):

• ciepło molowe przy stałym ciśnieniu (dla przemiany izobarycznej):

Jednostką ciepła molowego jest dżul na mol i kelwin:

Jest to ciepło molowe 1 mola substancji, którego temperatura wzrasta o 1 K po pobraniu przez niego 1 J ciepła.

Zależności między ciepłem molowym przy stałej objętości c_v i ciepłem molowym przy stałym ciśnieniu c_p:

Równanie Mayera - określa związek między c_p, c_v i R mówiący, że dla każdego gazu doskonałego różnica ciepła molowego przy stałym ciśnieniu i ciepła molowego przy stałej objętości jest równa uniwersalnej stałej gazowej:

c_p jest większe od c_v, ponieważ przy stałym ciśnieniu (a zmiennej objętości) nie cała energia dostarczona na sposób ciepła ma wpływ na wzrost temperatury gazu - część energii zostaje zużyta na wykonanie pracy.

Pojemność cieplna C - stosunek ilości ciepła Q dostarczonego ciału (układowi), do zmiany jego temperatury ∆T:

Pojemność cieplna C ciała o masie m zawierającego n moli substancji jest równa:

c - ciepło właściwe,

c_m - ciepło molowe substancji tego ciała.

Bilans cieplny - zestawienie ilości ciepła doprowadzonego do układu i ilości ciepła odprowadzonego z układu.

Jeżeli między ciałami o różnych temperaturach, które są w kontakcie termicznym między sobą i tworzą układ odizolowany termicznie od otoczenia, następuje wymiana energii tylko na sposób ciepła, to jej ilość Q jest równa (co do wartości) przyrostowi energii wewnętrznej ∆U_n ciała o temperaturze niższej od pozostałych i jest równa zmniejszeniu energii wewnętrznej ∆U_w ciał o temperaturze wyższej. Powyższy warunek można zapisać w postaci:

.

Wyprowadzenie wzoru na obliczanie κ:

Równanie adiabaty:

Równanie izotermy:

Logarytmując, następnie różniczkując powyższe równania otrzymujemy następujące związki:

Przechodząc do przyrostów skończonych otrzymamy:

Dzieląc oba równania stronami otrzymamy:

Sposób wykonania ćwiczenia:

Pomiar stosunku c_p / c_v , tj. stosunku ciepła właściwego przy stałym ciśnieniu do ciepła właściwego przy stałej objętości, przeprowadza się przez podanie powietrza w butli kolejno przemianom adiabatycznej /1 - 2/ i izochorycznej /2 - 3/.

Rozprężanie adiabatyczne od ciśnienia p+h /p - ciśnienie atmosferyczne, h - różnica ciśnień wskazana przez manometr cieczowy/ i objętości V od ciśnienia atmosferycznego p i objętości V' przebiega zgodnie z prawem Poissona:

W trakcie przemiany adiabatycznej temperatura gazu ulega obniżeniu i poprzez pozostawienie butli zamkniętej w temperaturze otoczenia realizuje się przemiana izochoryczna, w wyniku której powietrze w butli ponownie osiąga temperaturę otoczenia, końcowy punkt izochory o ciśnieniu p+h' / na wykresie punkt 3/ musi leżeć na tej samej izotermie co punkt 1, co oznacza że musi być spełnione prawo Boyle'a i Mariotte'a:

Z prawa Poissona oraz prawa Boyle'a i Mariotte'a wynika związaek:

Tabela wyników pomiarów:

Lp.	h [mm]	h' [mm]	h - h' [mm]
1	27	5	22	1,227
2	25	5	20	1,250
3	24	4	20	1,200
4	27	6	21	1,286
5	26	5	21	1,238
6	26	6	20	1,300
7	26	6	20	1,300
8	27	5	22	1,227
9	25	5	20	1,250
10	24	4	20	1,200
	h = 25,7 ∆h = ± 0,5	h' = 5,1 ∆h' = ± 0,5		κ = 1,2478 σ = ± 0,0118 ∆κ = ± 0,0266

Wyznaczam wartość średnią κ:

i - numer pomiaru,

n - ilość pomiarów.

Wyznaczam odchylenie standardowe od wartości średniej κ:

i - numer pomiaru,

n - ilość pomiarów.

Wyznaczam niepewność pomiaru κ metodą Studenta-Fishera dla poziomu ufności α = 0,95:

Wartość współczynnika t_αn = 2,262.

∆κ = ± 0,0266

Wyznaczam niepewność procentową pomiaru:

WNIOSKI:

Wykonane przeze mnie pomiary obarczone są niepewnościami. Spowodowane są one niedokładnością eksperymentatora, panujący w danym momencie warunkami otoczenia, niedokładnością sprzętu. W butli, której używałam do wykonania doświadczenia, znajdowała się skroplona para wodna. Ten fakt miał również wpływ na wyniki moich pomiarów. Mimo tego wyniki pomiarów obarczone są stosunkowo małą niepewnością (około 2%).

---