Podstawy z wytrzymałości materiałów do projektowania prętów z uwagi na stan graniczny zniszczenia.
IV.4. Wymiarowanie przekrojów prętów przy obciążeniach prostych i złożonych
Zasada superpozycji
Jeśli do danej bryły o ustalonych więzach przyłożono, w dowolnej kolejności, układy sił zewnętrznych
; k =1,2...n i dla każdego układu znane jest rozwiązanie zagadnienia brzegowego liniowej teorii sprężystości:
,to pola tensorowe naprężeń i odkształceń oraz pole wektorowe przemieszczeń określają relacje:
;
;
Zasada de Saint Venanta
Jeżeli do bryły przyłożone jest na małej powierzchni ΔS << S obciążenie wywołujące pewien stan naprężenia, odkształcenia i przemieszczenia i jeśli na tej powierzchni ΔS obciążenie zastąpimy innym, ale statycznie równoważnym, to wartości naprężeń, odkształceń i przemieszczeń wywołanych drugim obciążeniem, w dostatecznej odległości od miejsca przyłożenia sił, będą się różnić dowolnie mało od wartości odpowiednich wielkości wywołanych obciążeniem pierwszym.
Stan graniczny - stan, w którym konstrukcja lub jej część przestaje spełniać swoje funkcje lub gdy nie odpowiada założonym warunkom użytkowania.
Stan graniczny nośności - utrata stateczności, zniszczenie najbardziej wytężonych przekrojów
Stan graniczny użytkowania obejmuje: ugięcia, zarysowanie, drgania
Rodzaje obciążeń:
Czyste i proste rozciąganie i ściskanie:
Czyste rozciąganie - pręt obciążony tylko na ściankach poprzecznych siłami o równomiernie rozłożonej gęstości (q=const)
Macierz naprężeń Macierz odkształceń
Proste rozciąganie - rozwiązanie czystego rozciągania redukujemy do środka ścianki poprzecznej (N=qA => q=N/A )
N -siła, A- powierzchnia ścianki poprzecznej
Warunki projektowania: -stan graniczny zniszczenia
; - stan graniczny użytkowania
Czyste zginanie
Przy prostym zginaniu:
Warunki projektowania: -stan graniczny zniszczenia:
wskaźnik wytrzymałości:
wytrzymałość na:
- rozciąganie,
-ściskanie
- stan graniczny użytkowania:
- max. ugięcie (strzałka ugięcia )
Zginanie ukośne
Mimośrodowe rozciąganie i ściskanie
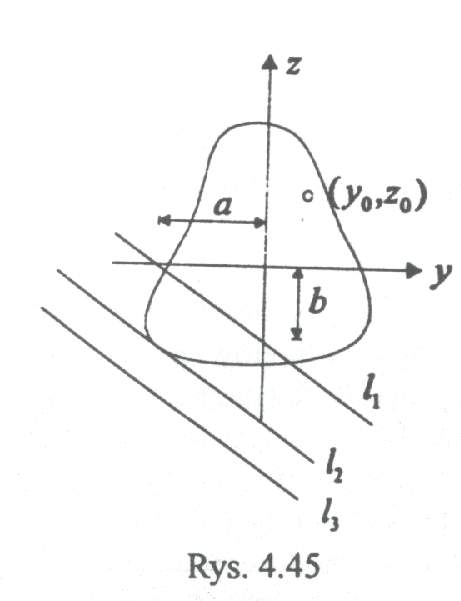
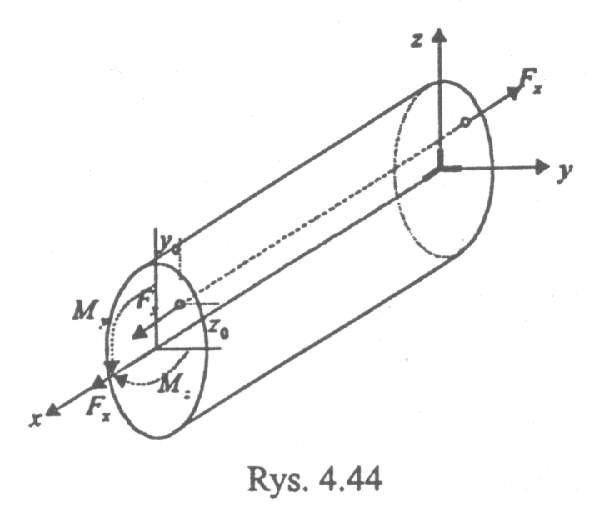
Oś obojętna - krawędź przecięcia płaszczyzny naprężeń z płaszczyzną przekroju poprzecznego. Równanie osi obojętnej σx =0
Może zajmować trzy położenia:
Przechodzi przez przekrój poprzeczny - prosta l1 - dzieli pole przekroju poprzecznego na dwie części, w których naprężenia σx mają przeciwne znaki (σx dodatnie czyli rozciąganie nad osią, część poniżej osi jest ściskana ( - ).
Jest styczna do konturu przekroju poprzecznego - prosta l2 naprężenia we wszystkich punktach przekroju
Przechodzi poza przekrojem poprzecznym - prosta l3 poprzecznego są tego samego znaku (+)rozciąganie
Zginanie poprzeczne - pręt pryzmatyczny, prosty, o przekroju poprzecznym symetrycznym wzgl. osi z , obciążenie przyłożone symetrycznie wzgl. płaszczyzny xz na pobocznicy i ściankach poprzecznych
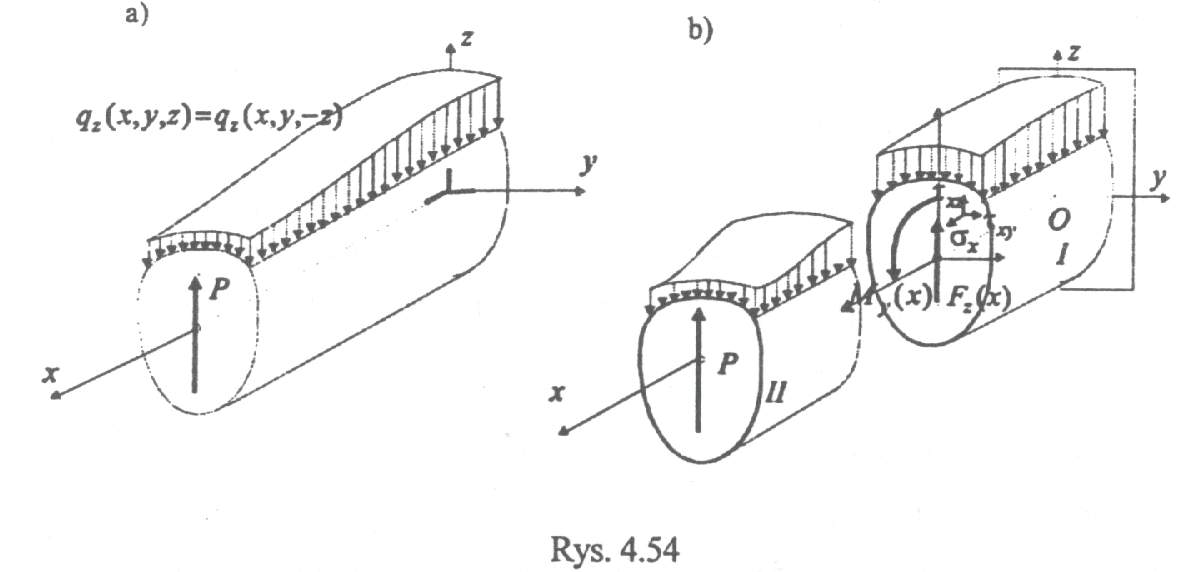
Czyste i proste skręcanie
czyste skręcanie - pręt prosty, pryzmatyczny, o dowolnym przekroju poprzecznym, obciążony siłami o gęstości
,przyłożonymi na ściankach poprzecznych.
Z pręta wycinamy walec, którego tworzące, po przyłożeniu obciążenia stają się liniami krzywymi,( na rys. linia n-n, krzywa n-n'), w dowolnym przekroju poprzecznym, punkt A przemieści się do p.A”, który wychodzi poza płaszczyznę przekroju, p.A' oznacza rzut p.A'' na naszą płaszczyznę przekroju poprzecznego.
-kąt skręcania :
,
-jednostkowy kąt skręcania
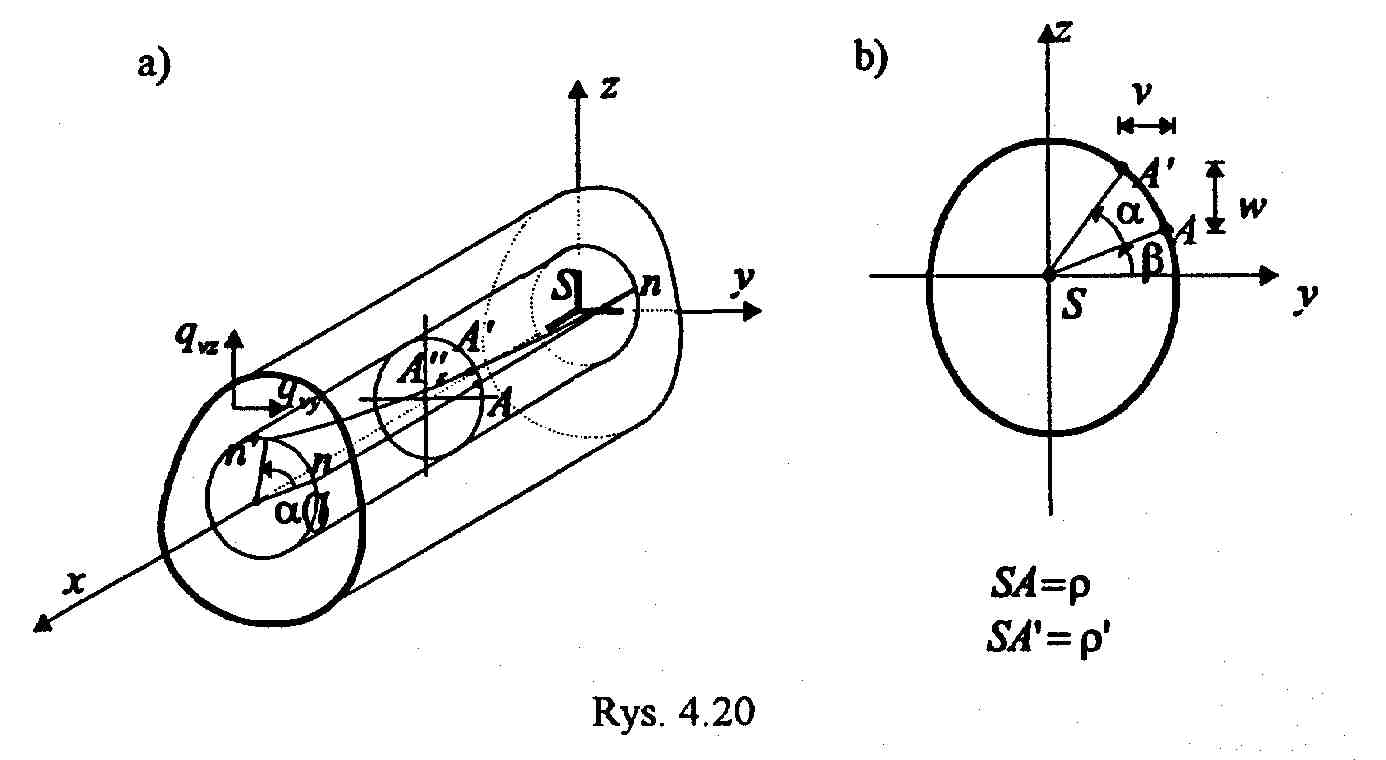
funkcje przemieszczeń :
,
,
pole odkształceń: z równań Cauchy'ego
otrzymujemy
,
,
,
,
,
pole naprężeń: z równań Hooke'a
mamy
,
,
,
,
,
zagadnienie brzegowe - spełnienie równań Naviera i statycznych warunków brzegowych zależy od odpowiedniego doboru
funkcji
,
, i,j =1,2,3 czyli
zagadnienie Neumanna
proste skręcanie -obciążenie momentami skupionymi równoważnymi z obciążeniem jak przy czystym skręcaniu
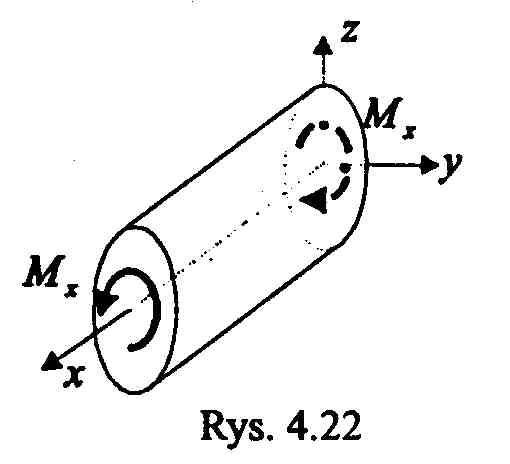
podstawiając jednostkowy kąt skręcania
do czystego skręcania otrzymujemy rozwiązanie przemieszczeń, odkształceń i naprężeń
skręcanie pręta o przekroju kołowym
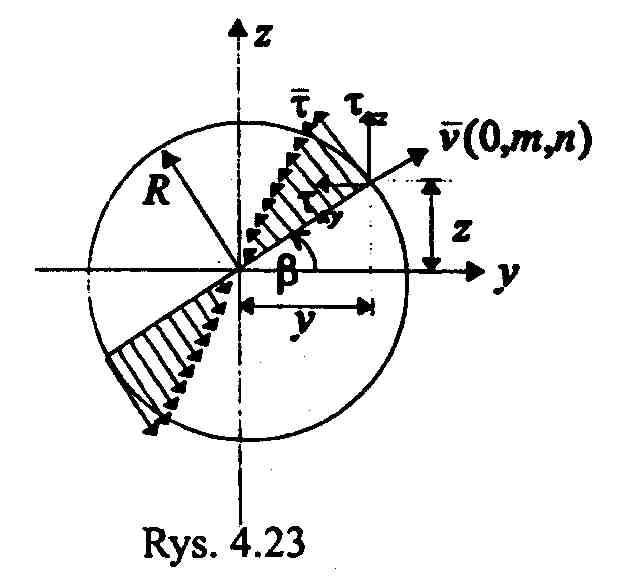
- biegunowy moment bezwładności
przemieszczenia :
,
,
odkształcenia :
,
,
,
naprężenia :
,
,
,
warunek projektowania : -stan graniczny zniszczenia
(
wskaźnik wytrzymałości przy skręcaniu) ; -stan graniczny użytkowania - nieprzekroczenie dopuszczalnego kąta skręcania
:
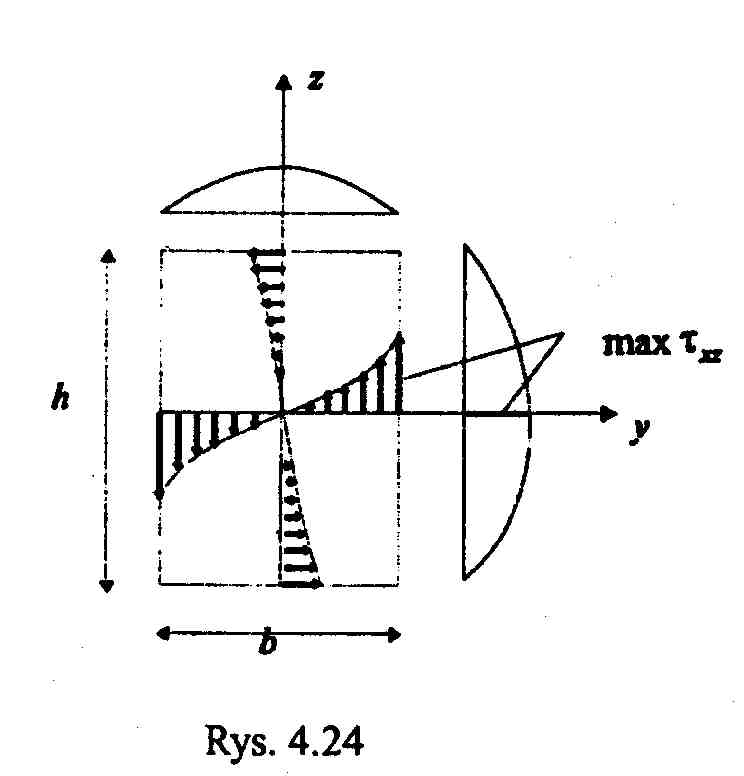
skręcanie pręta o przekroju prostokątnym
(
wskaźnik wytrzymałości przy skręcaniu pręta prostokątnego )
warunek projektowania : -stan graniczny zniszczenia
Hipotezy wytężeniowe -o wytężeniu materiału decyduje:
Rk = ( RH , Rs , Re , Rm )
Galileusz - maksymalna, bezwzględna wartość naprężenia głównego
Coulomb-Tresca-Guest - maksymalna, bezwzględna wartość największego naprężenia stycznego
np. betonowa próbka w kształcie walca poddana ściskaniu(ekstremalne naprężenia styczne leżą w płaszczyznach przekroju, które przechodzą przez jedną z osi głównych, a do pozostałych nachylone są pod kątem 45° - tworzą się dwa charakterystyczne stożki),zniszczenie następuje na pobocznicy tych stożków.
Huber-Mises-Hencky - ilość nagromadzonej w nim energii odkształcenia postaciowego
Niezależnie czy wartość ta powstała w wyniku prostego czy złożonego obciążenia
z q=const. z
N N
x
x
q=const. czyste rozciąganie proste rozciąganie
z z
M zg
x y
zd
czyste zginanie zginanie proste
z
Mz
My y
Wyszukiwarka
Podobne podstrony:
daneA dla grupy 1, semestr 4, Podstawy wytrzymałości materiałów, Wytrzymałość Materiałów (Mati K87),
Podstawy budownictwa materialy do wykladu PRAWO wydr
Materiały do projektu 1, Inżynieria Środowiska, Migracje Zanieczyszczeń
2 materiały do projektowaniaid 21141 ppt
Materiały do projektu fundamentu bezpośredniego
Materialy do projektu
Materiały do projektu 4
elementy struktury organizacyjnej do prezentacji, podstawy zarządzania, materiały do prezentacji
wytrzymalosc mat egzam sciaga, PWR [w9], W9, 5 semestr, Podst.wytrzym.mat. C, Podstawy wytrzymalości
przykładowe testy Podstawy Ekonomii, MATERIAŁY DO NAUKI
[PZ] materiały do projektu, administracja, Reszta, Promocja zdrowia
PWM, semestr 4, Podstawy wytrzymałości materiałów
Materiały do projektu 2
BO sem V materialy do projektu 2
[PZ] materiały do projektu - ankiety, administracja, Reszta, Promocja zdrowia
Pytania - podstawy ekonomii, MATERIAŁY DO NAUKI
więcej podobnych podstron