Sprężynami nazywamy elementy wykonane z materiału sztywnego (o dużym module sprężystości) oraz o odpowiednim kształcie.

Sprężyny stosowane w budowie maszyn i urządzeń spełniają następujące zadania:

• umożliwiają wzajemne przesunięcie elementów współpracujących

• kasują luzy

• wywierają naciski

• łagodzą uderzenia i wstrząsy

• tłumią drgania

• akumulują energię

• służą do wykonywania określonych prac, regulacji.

Rozróżniamy sprężyny zależnie od:

• przestrzeni zajmowanej przez nią

(walcowe, stożkowe, o kształcie pierścienia, płytki, drążka i płaskownika)

• linii wygięcia osi

(śrubowe, spiralne, proste łukowe, kątowe, ceowe)

• kształtu przekroju pręta

(sprężyny o przekroju okrągłym, kwadratowym, prostokątnym)

• zmienności przekroju na długości pręta

(sprężyny o stałym lub zmiennym przełożeniu)

• liczby elementów współpracujących

(sprężyny pojedyncze lub zespołowe)

• sposobu obciążenia całości sprężyny

(ściskane, rozciągane, skręcane i zginane)

• rodzaju dominujących naprężeń występujących w przekroju pręta sprężyny

(sprężyny o pręcie skręcanym, zginanym, rozciąganym, ściskanym).

Sprężyny pod działanie siły odkształcają się, ale po jej odjęciu powracają do pierwotnego stanu. W związku z tym dla sprężyn określamy ich sztywność (c), która jest stosunkiem przyrostu obciążenia do przyrostu odkształcenia:

[Nm]

W wyniku odkształcenia wywołanego obciążeniem sprężyna gromadzi energię umożliwiającą wykonanie określonej pracy. Praca odkształcenia wynosi:

SPRĘŻYNA ŚRUBOWA

Do podstawowych parametrów sprężyny śrubowej należą:

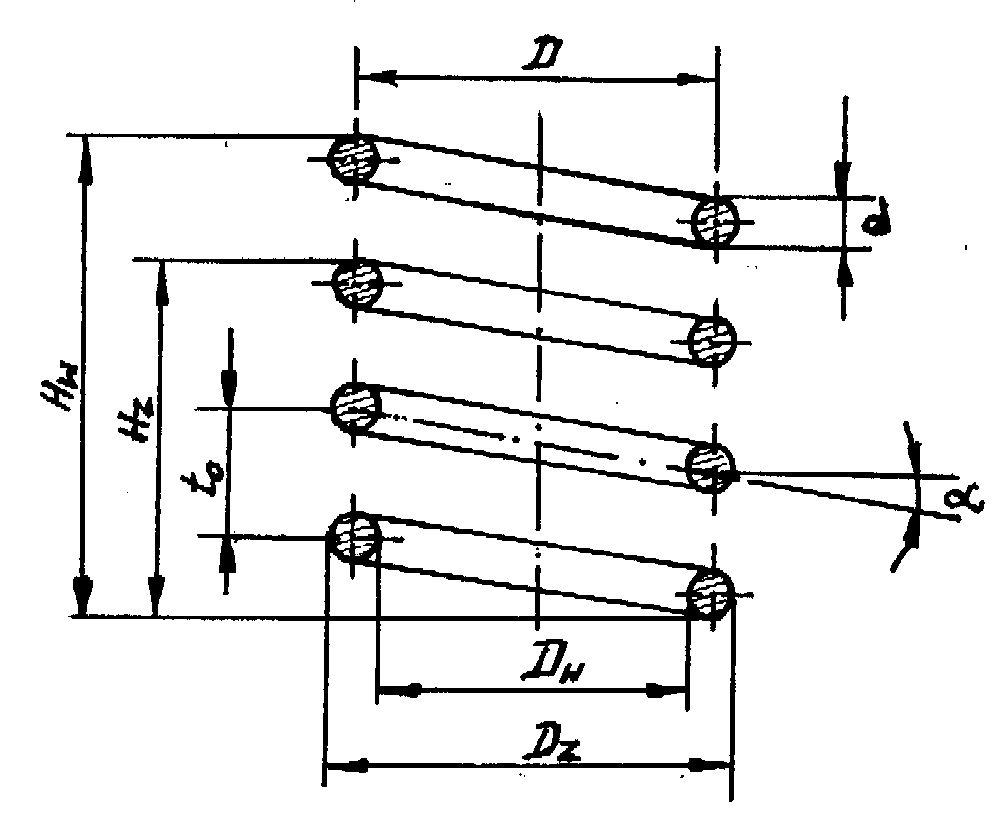
d - średnica otworu

D - średnica zwoju sprężyny

α - kąt wzniosu linii śrubowej zwoju

t_o - skok zwoju

D_w - średnica wewnętrzna

D_z - średnica zewnętrzna

H_w - długość sprężyny bez obciążeń

H_z - długość sprężyny zwartej

i - liczba czynnych zwojów

RYS. PARAMETRY GEOMETRYCZNE SPRĘŻYN ŚRUBOWYCH

Ze względów wytrzymałościowych sprężyny śrubowe obliczamy na skręcanie

[Nm]

współczynnik kształtu pręta

dop. naprężenia dla pręta

prostego uwzględniające

wymiary i warunki obciąenia

Strzałkę ugięcia obliczamy ze wzoru:

[m]

Zdolność akumulowania energii określamy wzorem:

[J/m³]

PRZEBIEG ĆWICZENIA

Badanie sprężyn przeprowadziliśmy na specjalnym przyrządzie.

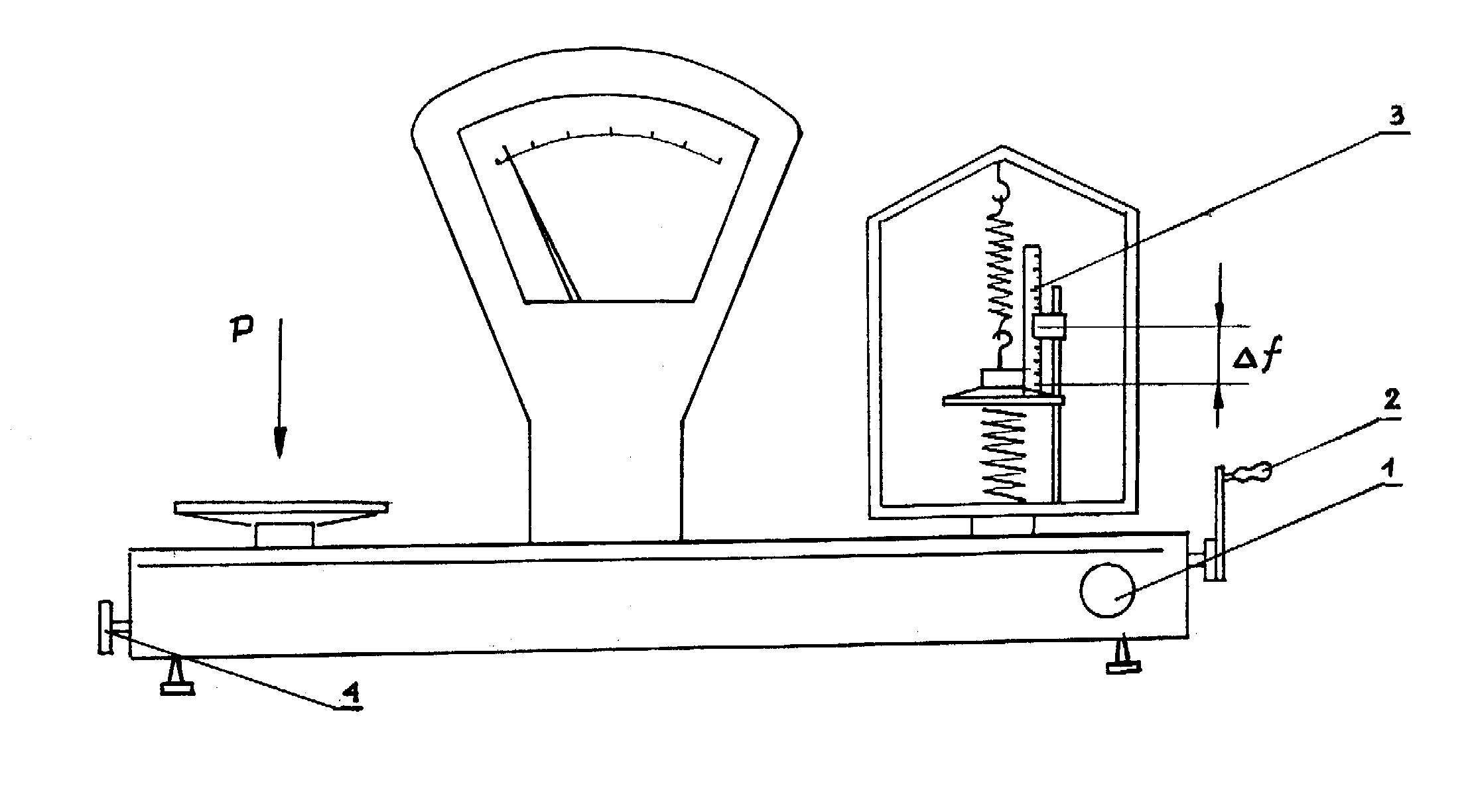
RYS. WAGA POMIAROWA

1.,2. POKRĘTŁA REGULACJI STANU RÓWNOWAGI

3. PRZYMIAR KRESKOWY

4. POKRĘTŁO DO ZEROWANIA WAGI

1. Wypoziomować wagę.

2. Wyzerować wagę (pokrętło 4).

3. Umieścić sprężynę pomiarową (rozciąganą) w pałąku pomiarowym.

4. Obciążyć lewą szalkę odpowiednim obciążnikiem.

5. Doprowadzić przyrząd do stanu równowagi (wskazówka w położeniu 0) poprzez regulację pokrętłami (1i 2).

6. Odczytać wartość strzałki ugięcia na przymiarze kreskowym (3).

7. Zwiększać kolejno obciążenie.

8. Podczas badania sprężyny ściskanej umieścić ją między tarczami pomiarowymi i postępować jak poprzednio.

Lp.	Obciążenie P[N]	Sprężyna naciągowa f[m]	Sprężyna ściskowa f[m]
1.	4,8	0,0001	0,00015
2.	9,6	0,0002	0,00025
3.	14,7	0,0007	0,0004
4.	19,6	0,00105	0,0005
5.	24,5	0,0014	0,00055

	d[m]	Dz[m]	Dw[m]	Hw[m]	i	to[m]	L/V [J/m^3]
sprężyna naciągowa	0,0018	0,015	0,011	0,063	35	0,0018	360∗10^8
sprężyna naciskowa	0,0025	0,025	0,0204	0,037	5	0,008	315∗10^8

Obliczenia zdolności akumulowania energii

1. Sprężyna naciągowa

dla stali sprężynowej węglowej 55 k_s=120 MPa

współczynnik G=8∗10⁴ MPa

1.Sprężyna naciskowa

5

---