WYZNACZENIE SIŁY KRYTYCZNEJ SPRĘŻYSTEGO WYBOCZENIA GIĘTNEGO I SKRĘTNEGO.

1.1.

Wstęp .

Wyboczenie sprężyste bisymetrycznego pręta jednoprzęsłowego o stałym cienkościennym przekroju otwartym i dowolnych warunkach podparcia na końcach , ściskanego osiowo stałąsiłą P , opisuje układ równań różniczkowych ;

EI_xy^IV + P_y^II = 0

EI_yy^IV + P_x^II = 0

_^V + (Pi_o² - GI_s)^II = 0

x,y, - przemieszczenia liniowe wzdłuż osi x , y oraz kątowe w płaszczyźnie xy.

II , IV - drugie oraz czwarte pochodne danych przemieszczeń.

i_o - biegunowy promień bezwładności względem środka ciężkości przekroju .

E,G - moduły sprężystości podłużnej i poprzecznej .

I_x,I_y,I_,I_s - momenty bezwładności.

Pierwsze równanie jest równaniem różniczkowym wyboczenia giętnego w płaszczyźnie yz , drugie - wyboczenia giętnego w płaszczyźnie xz , a trzecie - wyboczenia skrętnego pręta.

Rozwiązując te równania wyznaczyć można trzy wzajemnie niezależne wartości obciążenia P(Px,Py,P) , z których obciązenia najmniejsze , zwane krytycznymi dla rozpatrywanego pręta , przedstawić można wzorami:

• 
  siła krytyczna wyboczenia giętnego w płaszczyżnie yz,

- siła krytyczna wyboczenia giętnego w płaszczyżnie xz,

gdzie:

l - długość teoretyczna pręta ,

_x , _{y ,} _ - współczynniki długości wyboczeniowej.

Współczynniki długości wyboczeniowej _ przyjmują wartości:

• dla przegubowego podparcia obu końców pręta - 1,0

• dla przegubowego podparcia jednego , drugi zamocowany sztywno - 0,6992

• dla sztywnego zamocowania obu końców - 0,5

• dla sztywnego zamocowania jednego końca , drugi jako swobodny - 2,0

Smukłości pręta ;

• przy wyboczeniu giętnym w płaszczyźnie yz

• przy wyboczeniu giętnym w płaszczyźnie xz

Z trzech sił krytycznych znaczenie praktyczne dla rozpatrywanego pręta będzie miała siła o najmniejszej wartości , sile tej będzie odpowiadać największa wartość smukłości.

1.2.

Wyznaczenie obciażenia krytycznego wyboczenia giętnego.

Zakładamy , że pręt w płaszczyźnie mniejszej sztywności zginania ma taką krzywiznę początkową , że kształt jego osi w stanie nie obciążonym można przedstawić wzorem :

Wyrażenie to zostało dobrane w ten sposób , że spełnia warunki podparcia pręta. Jeżeli pręt zostanie obciążony siłą ściskającą P , to odchylenie osi pręta od stanu prostoliniowego wyniesie:

Wprowadzenie zastępczego obciążenia poprzecznego pręta o intensywności:

które jest równoważne wpływowi krzywizny początkowej na linię ugięcia pręta x(z) umożliwia przedstawienie równania różniczkowego linii ugięcia pręta w postaci:

Ogólne rozwiązanie równania otrzymamy za pomocą przekształcenia Laplace`a , a po wprowadzeniu do ogólnego rozwiązania stałych całkowania , wyznaczonych z warunków wynikających ze sposobu podparcia rozpatrywanego pręta i uwzględnienie warunku  = 1,0 otrzymamy równanie linii ugięcia:

Na podstawie powyższego wzoru wyznaczyć można ugięcie w połowie długości pręta δ=x(0,5l) , ugięcie to wyniesie:

Wprowadzenie zależnosci δ = f(P) , która dla P<P_ykr przedstawia się w postaci wykresu , który służy do doświadczalnego wyznaczenia obciążenia krytycznego wyboczenia giętnego pręta.

Doświadczalne wyznaczenie obciążenia krytycznego wyboczenia giętnego pręta przeprowadzić można także za pomocą metody Southwella . W metodzie tej wykorzystuje się wzór na ugięcie , któremu nadaje się postać równania:

Równanie to jest liniowe względem współrzędnych δ/P oraz δ , wyznaczona zostaje więc prosta o współczynniku kierunkowym tgγ = P_ykr

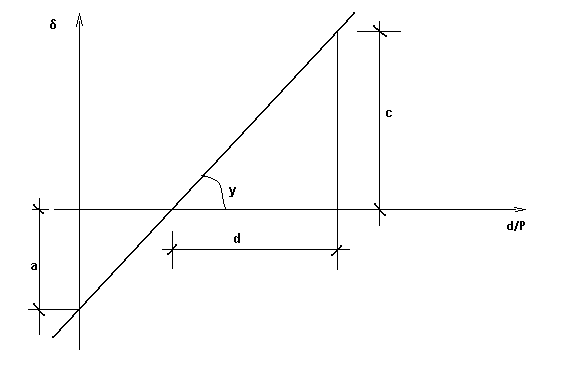
Określenie więc podczas badań , w postaci dyskretnej , zależności δ_i = f_i(δ_i/P_i) , a następnie aproksymacja otrzymanych wyników prostą:

której parametry  ,  obliczamy np. metodą najmniejszych kwadratów , umożliwia wyznaczenie wartości obciążenia krytycznego oraz krzywizny początkowej pręta z równości ;

P_ykr^d =  , a = 

1.3.

Cel i przebieg ćwiczeń.

Celem ćwiczeń jest doświadczalne wyznaczenie metodą obciążeń krytycznych sprężystego wyboczenia giętnego dla jednoprzęsłowych , osiowo ściskanych prętów o cienkościennym przekroju otwartym , podpartych przegubowo na obu końcach .

Dla pręta o przekroju w kształcie wąskiego prostokąta będzie to obciążenie krytyczne wyboczenia giętnego w płaszczyźnie mniejszej sztywności zginania.

Schemat stanowiska:

W celu wykonania ćwiczenia należy:

1. zmierzyć długość i wymiary przekroju poprzecznego pręta,

2. obliczyć moment bezwładności Iy przekroju poprzecznego,

3. obliczyć wartość siły krytycznej P_ykr ( w MN )

4. sprawdzić prawidłowość podparcia pręta i działanie czujnika zegarowego,

5. odnotować wskazanie czujnika jako w_o,

6. obciążyć pręt (w ćwiczeniu co 800 N ) i przy każdorazowym dociążeniu odczytać wskazania czujnika zegarowego.( pręt obciążyć do wartości około 0,7P_ykr ).

7. Wyniki zestawić w tabeli.

8. Sporządzić wykres δ w funkcji δ/P

9. Wyznaczyć na podstawie wykresu siłę krytyczną P_ykr^d (wMN)

10. Obliczyć procentową różnicę między wartością siły krytycznej wyznaczonej teoretycznie i doświadczalnie:

WYKONANIE ĆWICZENIA:

A.

• pręt o przekroju prostokąta 5,1 x 12,0 mm o długości 199,0 mm

B.

• Iy = hg³/12 = 12,0 * 5,1³/12 = 132,65 mm⁴

C.

P_ykr = ²Eiy / (_y*i)² = 3,14²*205*132,65/(1,0*199)² = 6,77 kN

D.

Pręt zamocowany poprawnie

E.

Początkowe wskazania czujnika L-lewy = 5,73 P-prawy = 4,97

F.

Nr	L-czujnik	P-czujnik	Siła P
0	5,73	4,97	0
1	5,90	4,81	80
2	6,00	4,71	160
3	6,19	4,52	240
4	6,53	4,18	320
5	6,85	3,87	400
6	7,73	2,98	480
7	6,77	3,95	400
8	6,25	4,46	320
9	6,08	4,64	240
10	5,93	4,78	160
11	5,80	4,90	80
12	5,78	4,93	10

G.

Lp.	Obciążenie w kg	Siła ściskająca w N	Wskazanie czujnika	Ugięcie pręta	δi/Pi (5/3)
1	2	3	4	5	6
1	0	0	5,73	0	0
2	80	800	5,90	0,17	0,0002125
3	160	1600	6,00	0,27	0,0001688
4	240	2400	6,19	0,46	0,0001917
5	320	3200	6,53	0,8	0,00025
6	400	4000	6,85	1,12	0,00028
7	480	4800	7,73	2,0	0,0004167
8	400	4000	6,77	1,04	0,00026
9	320	3200	6,25	0,52	0,0001625
10	240	2400	6,08	0,35	0,0001458
11	160	1600	5,93	0,2	0,000125
12	80	800	5,80	0,07	0,0000875
13	10	100	5,78	0,05	0,0005

---