METODY OBLICZENIOWE - MATERIAŁY DO ZALICZENIA WYKŁADÓW.

1. Zasady metody przemieszczeń:

1. Stan geometryczny układu prętowego można określić poprzez kąty obrotu węzłów swobodnych i ich przemieszczenia. Wielkości te stanowią tzw. niewiadome geometryczne. Niewiadome te są ulokowane w wektorze przemieszczeń układu q.

2. W metodzie przemieszczeń pomijamy odkształcalność podłużną prętów (element pod wpływem obciążenia nie zmienia swojej długości).

3. Liczba niewiadomych geometrycznych określa stopień geometrycznej niewyznaczalności.

2. Niewiadome metody przemieszczeń - przemieszczenia, obroty i przesuwy węzłów konstrukcji. Określenie liczby niewiadomych łączy się z podziałem konstrukcji na węzły i elementy.

3. Zasada podziału konstrukcji - podział konstrukcji na węzły i elementy jest dowolny, ale w obliczaniu konstrukcji za pomocą tradycyjnej metody przemieszczeń dążymy do jak najmniejszej liczby niewiadomych, aby układ równań, który rozwiązujemy był możliwie najmniejszy.

4. Wektor przemieszczeń układu - wektor zawierający niewiadome przemieszczenia
   

5. Wektor obciążeń układu - wektor sił działających w węzłach układu w kierunku przemieszczeń
   

6. Wektor przemieszczeń elementu - wektor przemieszczeń na końcach elementu skończonego
   

7. Wektor sił elementowych - wektor zawierający siły przywęzłowe
   

8. Dyskretyzacja prętowego układu konstrukcyjnego - Podział układu na zbiór węzłów i elementów. Z węzłami związany jest wektor przemieszczeń i obciążeń węzłowych. Z elementami związany jest wektor przemieszczeń i obciążeń elementowych.

9. Na co zwracać uwagę przy podziale układu konstrukcyjnego - przy podziale układu konstrukcyjnego na elementy spotykamy problem wyboru elementu. Wybór elementu zależy od typu rozwiązywanego układu. W zależności od modelu konstrukcji istotna jest liczba stopni swobody węzła.

10. Stopnie swobody - liczba niewiadomych w węźle.

1. Kratownice płaskie - dwa stopnie swobody w węźle

2. Kratownice przestrzenne - trzy stopnie swobody w węźle

3. Ruszty załamane w planie - trzy stopnie swobody w węźle

4. Ramy płaskie - trzy stopnie swobody w węźle

5. Ramy przestrzenne - sześć stopni swobody w węźle

11. Globalny układ współrzędnych - układ współrzędnych całego układu

12. Lokalny układ współrzędnych - układ współrzędnych poszczególnych elementów po dyskretyzacji układu.

13. Wektor obciążeń węzłowych - R=[M,0,P] siły występujące w węzłach ulokowane w wektorze w odpowiednich miejscach - tam gdzie niewiadome. Wektor q odpowiada R w danych układach.

14. Macierz sztywności i podatności układu - macierz sztywności to macierz zawierająca reakcje w założonych więzach od danego stanu przemieszczenia jednostkowego, macierz podatności zawiera przemieszczenia od danego jednostkowego obciążenia.

1. Pomiędzy wektorami q i R istnieje zależność, którą można zapisać macierzą sztywności - wektor
   

2. W układach geometrycznie niezmiennych macierz sztywności K jest macierzą nieosobliwą, oznacza to że jej wyznacznik jest różny od zera.

3. Istnieje zależność pozwalająca na uzyskanie macierzy podatności wykorzystując macierz sztywności,przy tym że macierz K musi być nieosobliwa
   ,gdzie F jest macierzą podatności układu.

4. Macierz sztywności musi być macierzą symetryczną - wynika to z tw. o wzajemności przemieszczeń

5. Macierz sztywności pojedynczego elementu skończonego jest macierzą osobliwą oznacza to ze jej wyznacznik jest równy zero

15. Metody wyznaczania macierzy sztywności:

1. Macierz sztywności K można wyznaczyć metodą jednostkowych stanów przemieszczeń

2. Macierz podatności można wyznaczyć metodą jednostkowych stanów obciążeń i skorzystać z zależności macierzy odwrotne
   , przy tym ze F musi być macierzą nieosobliwą.

16. Jaki sposób rozwiązania opłaca się stosować w układach statycznie niewyznaczalnych : bardziej opłacalne jest wyznaczenie macierzy podatności i odwracając ją uzyskać macierz sztywności układu.

17. Macierz sztywności elementu kratowego - macierz ta zawierz w każdym wyrazie element EA/l ,wektor S zawiera siły normalne, nie występują kąty obrotu oraz przemieszczenia prostopadle do elementu, wektor D zawiera przemieszczenia równoległe do osi elementu.

18. Macierz sztywności elementu belkowego - przemieszczenia w dowolnym punkcie można zapisać wielomianem 3 stopnia. Wektor S może zawierać siły normalne, prostopadłe oraz momenty, wektor D może zawierać przemieszczenia równoległe i prostopadłe oraz kąty

obrotu.

19. Symetria macierzy podatności wynika z twierdzenia o wzajemności przemieszczeń

20. Konsolidacja - proces zamiany równań dla pręta podstawowego w układzie równań dla pręta z przegubem.

21. Modyfikacja macierzy sztywności - uwzględnienie warunków podporowych. Zakładamy, że pewne przemieszczenia węzłowe są równe zero i modyfikujemy macierz poprzez wykreślenie wierszy i kolumn przy odpowiadających im zerowych przemieszczeniach.

22. Gdy zamiast podpory sztywnej mamy podporę sprężystą to - gdy układ jest podparty podporą sprężystą to uwzględnienie tej podpory uzyskujemy poprzez dodanie elementu Ks (czyli sztywności ) do wyrazu na głównej przekątnej macierzy w wierszu i kolumnie odpowiadającej danemu stopniowi swobody.

23. Transformacja układu współrzędnych - macierzowe równanie równowagi a co za tym idzie macierz sztywności elementu jest zapisywana w lokalnym układzie współrzędnych. Ponieważ równanie równowagi ma być zapisane we wszystkich węzłach i obowiązywać dla całego układu konstrukcyjnego istnieje potrzeba wprowadzenia globalnego układu współrzędnych i zapisania równań w tym układzie. Układ globalny założony jest już na początku rozwiązywania zadania.

Zmiana układu lokalnego na globalny na poziomie elementu wiąże się z transformacją macierzy sztywności i wektora obciążeń. Macierz T jest macierzą transformacji zawierającą w każdym elemencie cosinus (x,X),(x,Y),(x,Z) w pierwszym wierszu i cos(y,X),(y,Y),(y,Z) w drugi wierszu i analogicznie w trzecim wierszu cos(z,X) …. Macierz T jest macierzą ortogonalną.

24. Wektor alokacji - wektor zawierający adresy poszczególnych przemieszczeń lokalnych. Wiążę ze sobą przemieszczenia.

25. Agregacja - składanie macierzy sztywności układu z macierzy sztywności pojedynczych elementów

26. Algorytm rozwiązania zadania macierzową metodą przemieszczeń: (układ ramowy)

1. Wykonanie dyskretyzacji układu (podział na elementy)

2. Ustalamy jak będzie wyglądał wektor przemieszczeń globalnych Q oraz sił węzłowych

3. Dla każdego pręta budujemy wektor sił przywęzłowych S, macierz sztywności K oraz przemieszczeń D oraz So wektor sil przywęzłowych od obc. przęsłowych

- można dokonywać kondensacji macierzy (uwzględniając przeguby zewnętrzne)

- dokonywać transformacji (jak trzeba) do globalnego układu współrzędnych

- po wykonaniu czynności dla wszystkich prętów doprowadzimy do zbudowania wektora S,D i macierzy Ka oraz So

d) Budujemy macierz alokacji A - ustalamy jak sa powiązane D i Q

e) Obliczamy macierz K=Atransponowane*Ka*A oraz wektor Ro=Atrans*So

f) Jeżeli trzeba to dokonujemy modyfikacji układu równań - uwzględniając warunki podporowe

g) Rozwiązujemy układ równań K*Q=R-Ro

h) Budujemy wektor przemieszczeń przywęzłowych D=A*Q

oraz wyliczamy wektor sił przywęzłowych S=Ka*D+So

27. Kondensacja macierzy sztywności - zakładamy że pewne siły przywęzłowe równe są zero.

Macierz sztywności skondensowana np. względem wektora D jest w postaci :

K=K11-K12*K22do(-1)*K21

28. Macierz obrotu Jacobiego: macierz zbudowana z pochodnych cząstkowych (pierwszego rzędu) funkcji, której składowe to funkcje rzeczywiste. Jej wyznacznik (jakobian) znajduje zastosowanie w funkcjach wymiernych.

29. Metoda elementów skończonych (MES) :

1. Idea metody - dzielimy ciało na pewne podobszary zwane elementami skończonymi

- wprowadzamy podobną geometrię np. trójkąt trzywęzłowy. Trójkąty mogą się zbiegać tylko w narożnikach. Następnie dokonujemy połączenia w węzłach ciała (skończona ilość węzłów - metoda elementów skończonych)

30. Etapy rozwiązania metodą MES :

1. Kontinuum (ciało) podzielone zostaje w myśli liniami na pewną liczbę skończonych elementów

2. Zakłada się że elementy te połączone są ze sobą w skończonej liczbie punktów, znajdujących się na ich obwodach (nie zawsze w narożnikach).Przemieszczenia punktów węzłowych stanowić będą podstawowy układ niewiadomych.

3. Zostaje dobrana funkcja, funkcje określające jednoznacznie stan przemieszczeń wewnątrz każdego elementu skończonego w zależności od przemieszczeń punktów węzłowych. Funkcję tą nazywamy Funkcją kształtu, ta sama funkcja używana jest do zmiany kształtu elementu krzywoliniowego na prostoliniowy.

4. Funkcje przemieszczeń definiują jednoznacznie stan odkształceń wewnątrz elementów w zależności od przemieszczeń węzłów. Odkształcenia te wspólnie z odkształceniami początkowymi i własnościami sprężystymi materiału określają stan naprężeń w całym elemencie, a więc także na jego brzegu.

5. Zostaje określenie układu sił skupionych w węzłach równoważących napięcia na brzegach elementów oraz wszystkie inne siły działające na ciało i zostaje sformułowany związek, wiążący te siły z przemieszczeniami węzłów elementów za pomocą tzw. macierzy sztywności.

6. Następnie rozwiązanie powyższego układu równań da nam wektor q i powracając do punktu 4 ze znanymi już przemieszczeniami można wyznaczyć naprężenia elementu.

31. Metoda elementów skończonych - zasada dobierania siatki elementów skończonych i sprawdzenie dokładności

1. Elementy łączą się tylko w węzłach

2. Każdy element posiada tylko jedną wartość składowej naprężeń i odkształceń

3. Siatkę należy zagęścić tam gdzie spodziewamy się dużych naprężeń (przyłożenie sił skupionych oraz naroża konstrukcji)

4. Stosunek proporcji boków elementów : najdłuższy do najkrótszego a/b<=3

5. Sprawdzenie czy siatka jest dostatecznie dokładna - zasada podwójnego zagęszczenia siatki -zbudowanie jednego zadania za pomocą 2 różnych siatek i wtedy porównuje się wielkości naprężeń i odkształceń. Należy sprawdzić czy przemieszczenia otrzymane w siatce 1 i 2 nie różnią się o więcej niż 5 %. Siatkę zagęszczamy tak długo, aż uzyskamy rozbieżność wyników mniejsza niż te 5%. Najtrudniej uzyskać ten wynik w punktach przyłożenia sił. Zasada stałej odległości od punktów przyłożenia sił pozwala na wyznaczenie naprężeń nie dążących do nieskończoności

Rozmiar elementu skończonego musi być skończony - nie można wymodelować obszaru pół nieskończonego.

Należy założyć siatkę taką, aby warunki brzegowe nie miały wpływu na uzyskane wyniki (warunki brzegowe w miejscu gdzie przemieszczenie to N=0)

Zakładanie siatek dla elementów symetrycznych (ze względu na geometrie i obciążenie) :

- siatki także powinny być symetryczne inaczej będą błędne wyniki

Aby wyniki były dokładniejsze można siatkę dwukrotni zagęścić.

32. Co wykorzystujemy do wyznaczenia równań MES - należy wykorzystać zasadę pracy wirtualnej

33. Wnioski dotyczące Funkcji kształtu - dowolna funkcja kształtu należy tak dobrać aby dawała odpowiednie przemieszczenie węzłów i dla dowolnego węzła miała wartość 1 oraz 0 dla innych węzłów

34. Kryteria dobierania funkcji kształtu:

1. Powinny być dobrane tak, aby nie pozwalały na wytworzenie się stanu napięcia w elemencie jeżeli przemieszczenia węzłów powodują jedynie ruch elementów jako ciała sztywnego

2. Funkcja kształtu musi być dobrana tak, aby przy zgodności przemieszczeń węzłów z warunkiem stałych odkształceń można było otrzymać te same odkształcenia

3. Funkcja kształtu powinna być dobrana tak, aby odkształcenia na granicach między sąsiednimi elementami były skończone (choć nie muszą być określone)

35. Elementy w płaskim stanie naprężenia i odkształcenia

1. Element trójkątny z 3 węzłami : Przemieszczenie wewnątrz elementu uzależnione od q. Zakładamy, że przemieszczenia wewnątrz elementu nakładają się jako wielomian trzeciego stopnia. Na każdej krawędzi przemieszczenia muszą się rozkładać jako funkcja liniowa. Macierz przemieszczeń i odkształceń B nie zależy od punktu w którym przeprowadzamy obliczenia.

W każdym punkcie elementu trójkątnego z trzema węzłami w PSN lub PSO poszczególne składowe wektora odkształceń mają stałą wartość.

Powyższe sformułowanie jest zaletą ale też wadą -dla rzadkiej siatki jest małe przybliżenie wyników, więc należy stosować gęste siatki elementów skończonych.

36. Wektor odkształceń początkowych - podstawowe obciążenie np. obciążenie termiczne elementu ma temperaturę α i ogrzane o delta t

PSN: ε={αΔt, αΔt,0} PSO: ε0=(1+v){ αΔt, αΔt,0}

37. Analiza stanu naprężeń - trzeba określić właściwości materiału

1. Materiał izotropowy - właściwości jednakowe we wszystkich kierunkach np.stal

2. Materiał ortotropowy - różne właściwości w dwóch prostopadłych do siebie kierunkach np. drewno

38. Macierz konstytutywna [D]- (sprężystości) jest to macierz która opisuje właściwości materiałowe materiału z którego jest dany element

39. Gdy przyjmujemy układ wsp. w środku ciężkości to obciążenie powierzchniowe przyłożone na elementy rozkłada się równomiernie

40. Dlaczego met. rozwiązywania całki powierzchniowej wymagają met. startowej?

Ponieważ znamy tylko jeden warunek początkowy.

41. Problemy własne całkowania równań różniczkowych:

- powstaje duży błąd na każdym etapie obliczeń, przy czym rozróżniamy błąd metody i zaokrąglenia, ten błąd przenosi się na wyniki innych etapów

- problem oszacowania globalnego błędu na danym etapie obliczeń

- problem rozpoczęcia obliczeń związany z warunkiem początkowym, dla wielu metod potrzebna jest znajomość funkcji w kilku punktach - wymagana jest specjalna procedura startowa

- problem długości kroku (stabilność procesu poprzez odpowiednią długość kroku; krok musi być na tyle duży, aby krok obliczeń był racjonalny; problem zmiany długości kroku w trakcie obliczeń)

- problem całkowitego czasu obliczeń (dla dużych układów bardzo szybko rośnie)

42. Metody rozwiązywania równań różniczkowych:

1. Jawne: met. Różnic centralnych, met. Eulera, met. punktu środkowego, met. Rungego-Kutty

2. Niejawne: met. trapezów, met. Busfotha-Moultona, met. Newmarka

43. Metoda Różnic Centralnych:

Zapis równania ruchu w chwili t. Mamy 3 niewiadome:
Do tego r-nia na a i V w chwili t, w których zakładamy, że między chwilą t+ Δt i t- Δt prędkość była stała. Do r-nia Ruchu wstawiamy wektory
i otrzymujemy r-nie z 3 przemieszczeniami. Zaletą tej metody jest to,że jest ona szybka w obliczeniu. Nie wymaga odwrócenia macierzy sztywności. Wady:

1. Po prawej stronie występują 2 przemieszczenia w dwóch sąsiednich chwilach {qt} i {qt- Δt}

2. Met. Ta wymaga zastosowania procedury startowej*- pewne r-nie, które wykorzystujemy jednokrotnie w celu uzyskania 1szej wartości przemieszczeń (na początku)

3. Problem z układem równań różniczkowalnych a więc pojawia się problem zbieżności i stabilności

Stabilność - na każdym kroku rekurencyjnego obliczenia przemieszczeń popełniamy błędy. Jeżeli błedy sumują się tak, że rozwiązanie coraz bardziej odbiega od rozwiązania rzeczywistego, to mówimy że algorytm stał się Niestabilny.

Zbieżność- polega na określeniu, na ile rozw. numeryczne różni się od rozw. rzeczywistego w konkretnym kroku całkowania.

Metoda różnic centralnych jest metodą warunkowo stabilną. Oznacza to, że tylko dla pewnych wartości kroków całkowania uzyskujemy rozwiązania stabilne. Można udowodnić, że met. róż. centr. Jest stabilna gdy zastosowany krok całkowania Δt jest mniejszy od Δt kryt. (Δtcr), który można obliczyć dzieląc najkrótszy okres drgań własnych modelu przez π lub dzieląc 2 przez najwyższą częstość tych drgań.

44. 
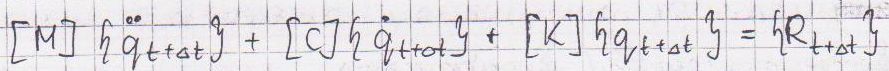
    Metoda Newmarka: równanie jest zapisywane w chwili t+Δt

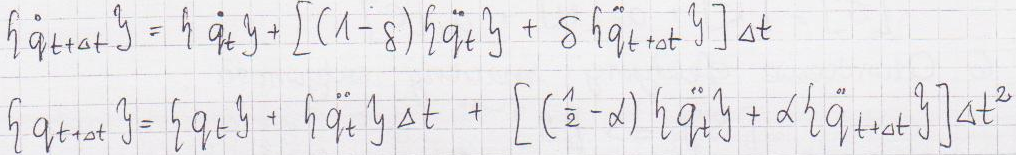
Do tego układu równań dochodzą 2 równania numeryczne na prędkość i przemieszczenie:

W tych dwóch równaniach pojawiają się współczynniki alfa i δ nazywane współczynnikami Newmarka - regulują one proporcje między wartościami w chwili t i t+Δt. Jeżeli δ>0,5 i alfa>0,25*( δ+0,5)² to można przyjąć, że metoda Newmarka jest bezwarunkowo stabilna. Możemy pozwolić sobie na większy krok całkowania, powoduje to, że w obliczeniach sprężystych met. Newmarka daje wynik znacznie szybciej.

45. Współczynnik nadrelaksacji:

Zazwyczaj używa się współczynnika z przedziału <1,2-1,45>

- gdy w=1 to metoda nadrelaksacji przechodzi w metodę Gaussa-Seidla

- gdy macierz współczynników w układzie równań jest symetryczna i dodatnio określona to met. nadrelaksacji jest zbieżna

46. Sposoby normalizacji wektorów własnych:

Każdy wektor własny jest określony z dokładnością do stałej k, gdzie k jest dowolną liczbą różną od 0. Ten współczynnik dobieramy, tak aby spełniony był jeden z warunków:

- suma kwadratów składowych wektora {x}^T = 1

- pierwsza składowa wektora {x}ⁱ=1

- największa składowa wektora {x}ⁱ=1

- suma modułów składowych wektora {x}ⁱ=1

47. Układy równań liniowych :

Sposoby rozwiązywania: Stosuje się metody ręczne : podstawienia i wyznaczników lub metody stosowane w komputerach :

- metody dokładne : dzielące się na dekompozycyjne (m.Gaussa-Crovta, Gaussa-Dolittle'a, Cholewskiego) oraz na eliminacyjne (Gaussa, Jordana)

- metody przybliżone : (metody iteracji prostej, metody Gaussa-Seidla, metoda Nadrelaksacji)

48. Metody dokładne rozwiązywania układów równań liniowych :

1. Metoda Gaussa : (metoda eliminacji ) i na końcu rekursja

- może się zdarzyć tak, że wyznacznik macierzy współczynników będzie różny od 0. Natomiast dzielnik z operacji akk=0.Wówczas należy przedstawić wiersze tak, aby na głównej przekątnej eliminowanego równania uzyskać akk do potęgi (k-1) różne od zera. Takie podstawienie zawsze uda się znaleźć.

- Jeżeli det A=0 to zmiana wierszy nie usunie dzielenia przez 0

- Jeżeli dzielnik ak=akk do (k) można zapamiętać na miejscu jedynki głównej przekątnej, to można łatwo wyznaczyć wyznacznik macierzy A

- Jeżeli macierz jest dodatnio określona, inaczej jeżeli wyznacznik jest >0 to wszystkie dzielniki ak>0 i otrzymujemy algorytm bez podstawień

- Liczba operacji matematycznych potrzebnych do rozwiązania układu metodą Gaussa wynosi n do potęgi (3).

2. Metoda Jordana : (metoda eliminacji) i na końcu brak rekursji

Polega na przekształceniu układu równań w macierz jednostkową a wektor prawych stron staje się bezpośrednio wektorem rozwiązań. Przekształcamy tu jednocześnie macierz prawych stron i współczynników

49. Metody dekompozycyjne rozwiązywania układów równań liniowych:

Metody dekompozycyjne - Rozłożenie macierzy A na dwie macierze trójkątne (dolną i górną). Każda nieosobliwa kwadratowa macierz A o rozmiarze n x n można rozłożyć na iloczyn dwóch macierzy trójkątnych jeżeli wszystkie minory główne macierzy A są różne od zera. Rozkładu można dokonać na n sposobów dobierając dowolnie n elementów z głównej przekątnej macierzy L lub U.

W metodach dekompozycyjnych mamy dwie rekursje. Rozkład tylko macierzy współczynników nie ruszając wektora P - nie musimy zmieniać

Wadą metod dekompozycyjnych jest - ze ma 2 kroki wsteczne.

1. Metoda Gaussa-Dolittle'a

-Każda nieosobliwa macierz A o rozwiązaniu n x n można rozłożyć na iloczyn dwóch macierzy trójkątnych jeżeli wszystkie minory główne macierzy są różne od zera. Rozkładu tego można dokonać na n sposobów dobierając dowolne n elementów na głównej przekątnej górnej lub dolnej macierzy trójkątnej.

2. Metoda Gaussa-Crouta

-dobieramy w macierzy U na głównej przekątnej same jedynki.

c) Metoda Choleskiego pozwala rozwiązać układ n równań liniowych z n niewiadomymi, w którym macierz współczynników jest symetryczna i dodatnio określona, tzn. A=A^H dla rzeczywistych A=A^T. Polega na znalezieniu dla macierzy współczynników układu A macierzy trójkątnej. Ten sposób rozwiązania układu równań ma wadę, że można ją tylko stosować, gdy macierz współczynników jest symetryczna i dodatnio określona.

50. Różnice w rozwiązywaniu metodą Gaussa i Newtona -

1. Met. Newtona (stycznych)- określa się w przedziale standardowym <-1,1>podzielonym na n równych części, w których należy znaleźć wartości funkcji, po czym za pomocą tych wartości wyznacza się odpowiedni wielomian interpolacyjny i całkuje się go algebraicznie.

2. Met. Gaussa-zamiast rozmieszczać punkty w jednakowych odległościach zakłada się ich rozstaw taki, aby zapewnić najlepsze przybliżenie do rzeczywistej wartości funkcji. Tak dobiera się ich odcięte i wagi funkcji, aby odpowiednia zależność była równości tożsamościową dla wielomianu potęgowego możliwie największego stopnia Wyniki rozwiązania są trudne do obliczenia dlatego zostały stabelaryzowane. Mala ilość funkcji do wyliczenia.

51. Metoda przybliżona i ścisła

Met. przybliżone - są dobre, gdy mamy duży układ równań, a macierz [A] ma wiele równych współczynników; - są dobre, gdy macierz [A] jest rzadka (wiele elementów = 0); - są niewrażliwe na błędy arytmetyczne w trakcie obliczeń, a błędy przyspieszają proces iteracji; - nie występują błędy zaokrągleń matematycznych związanych z przekształceniem układu równań; - są dobre do zastosowania komputerów o małej ilości pamięci

52. Metoda minimum lokalnego i met. Monte Carlo - porównanie:

Met. minimum lokalnego: - metoda zamknięta; - poszukuje się punktu, w którym funkcja osiągnie minimum w <a, b> z krokiem h; - jeśli funkcja maleje to posuwamy się dalej w tym samym kierunku z tym samym krokiem, jeśli nie to zawracamy i zmniejszamy długość kroku o połowę; - można wyznaczyć wszystkie pierwiastki, ekstrema w danym przedziale

Met. Monte Carlo: - metoda otwarta; - punkty w przedziale wybiera się losowo, a po każdym losowaniu zapamiętuje się najmniejszą wartość obliczeniową funkcji oraz wartość odpowiadającej jej zmiennej X; - przy dużej liczbie losowań udaje się znaleźć wartość bliską minimum; + stwarzamy szansę wylosowania punktów, które mogłyby być pominięte przy poszukiwaniu systematycznym; + daje szansę wylosowania minimum globalnego, an ie tylko minimum lokalnego; + może być stosowana do funkcji nieciągłych; - czasochłonna

53. Sposoby rozwiązywania całek:

- całkowanie met. Newtona-Cates'a

- met. Gaussa

- met. iteracyjne Rombego

- całkowanie bary centryczne

54. Co to są punkty Gaussa w całkowaniu numerycznym :

Zamiast rozmieszczać punkty w jednakowych odległościach zakłada się ich rozstaw taki aby zapewnić najlepsze przybliżenie do rzeczywistej wartości funkcji. Tak dobiera się ich odcięte i wagi funkcji,aby odpowiednia zależność była równością tożsamościową dla wielomianu potęgowego możliwie największego stopnia.

55. Metody rozwiązywania układów równań (wymienione) :

LINIOWE : dokładne a) met. eliminacji (Gaussa, Jordana)

b)met. dekompozycyjne (Gaussa-Crouta, Gaussa-Dolittla, Cholewskiego)

przybliżone (iteracji prostej Gaussa, Gaussa-Seidla, nadrelaksacji)

NIELINIOWE : a)zamknięte (poszukiwania, połowienia kroku, minimum lokalnego)

b)Otwarte (Monte-Carlo, siecznych, stycznych)

56. Wady i zalety metod iteracyjnych :

1. WADY : - nie zawsze jest proces zbieżny

- zbieżność może zależeć od wyboru wartości początkowych

- dla różnych układów równań różne metody pozwalają na uzyskanie szybszych wyników

b) ZALETY : - są dobre gdy mamy duży układ równań, a macierz A ma wiele równych współczynników

57. Metoda kolokacji :

Niech wartość funkcji y1,y2,y3 będą dane w punktach x1,x2,x3 szukamy funkcji y=f(x) w postaci kombinacji liniowej y=a1f1(x)+a2f2(x)+…anfn(x). Funkcje fi(x) są z góry założone.

Kolokacja wielomianowa fi(x)=x(do potęgi i-1) i =1,2,3…,n

58. Aproksymacja : sprowadzenie opisu do jednej takiej funkcji, aby błąd w opisie punktów uzyskanych z doświadczeń był najmniejszy, liczba punktów przewyższa ilość punktów potrzebnych do jednoznacznego określenia wzoru funkcji.

- jedna funkcja przybliżająca

- funkcja przechodzi tak, aby błąd przybliżenia punktów pomiarowych był jak najmniejszy

- znaczna liczba punktów pomiarowych

a) sposoby aproksymacji ze względu na sposób liczenia bledu :

- minimum sumy bledów

- minimum sumy wartości bezwzględnych bledów

- kryterium min i max > minimum największego błędu

- minimum sumy kwadratów -metoda najmniejszych kwadratów

A) metoda najmniejszych kwadratów :

- wartość funkcji y1…,yn dane są w punktach x1,….,xn

- szukamy funkcji jako kombinacji liniowej pewnych funkcji y=a1f1(x)+…..aifi(x),znanych funkcji f1(x)…,fn(x),różnica i<<n

- błąd i-tego równania

- wsp. ai dobieramy tak aby błąd był najmniejszy

- powstaje układ i równań z i niewiadomymi

- kontrola błędu : wariacja, odchylenie standardowe, rozwiązanie

- statyczna ocena rozwiązania : wartość średnia i kwadrat odchyleń, odchylenie standardowe i wariacja, wsp. wariacji, standardowy błąd przybliżenia, wsp. determinacji, wsp. korelacji, rozwiązanie

59. Interpolacja: polega na znalezieniu opisu takich funkcji, które przebiegają przez punkty doświadczalne. Takich punktów jest zazwyczaj za mało.

Charakterystyka :

- kilka funkcji przybliżających

- funkcje przechodzą przez wszystkie punkty pomiarowe

- niewielka liczba punktów pomiarowych

a) Rodzaje interpolacji :

- Interpolacja liniowa - przechodzi przez kolejne punkty, jest to zbiór funkcji y=f(x). Najprostsza metoda stosowana dla funkcji stablicowanych. Odległość między punktami jest stała.

- Interpolacja kwadratowa - wybór 3 najbliżej siebie leżących punktów o jednakowej odległości względem siebie i opisanie ich położenia za pomocą paraboli 2 stopnia.

- Interpolacja wielomianowa dowolnego stopnia n

---