Wyznaczanie stosunku ciepła właściwego gazu przy stałym ciśnieniu do ciepła właściwego przy stałej objętości (C_p/C_v)

Parametry termodynamiczne określające stan gazu to: ciśnienie p, temperatura T w skali bezwzględnej i objętość V. Ciśnienie i temperatura są to wielkości makroskopowe, których sensu fizycznego należy szukać w teorii kinetyczno-molekularnej budowy substancji. Według tej teorii czą­steczki gazu są w ciągłym bezładnym (chaotycznym) ruchu. Cząsteczki gazu doskonałego nie oddziałują miedzy sobą, a przy spotkaniu zderzają się sprężyście. Przy zderzeniach sprężystych ze ścianką naczynia zachodzi zmiana pędu cząsteczek gazu. Zgodnie z II zasadą dynamiki zmiana pędu ciała równa się popędowi siły, czyli na ściankę naczynia działa siła. Siła ta podzielona przez pole powierzchni ścianki jest ciśnieniem p, jakie wywiera gaz na ściankę naczynia. Dla gazu doskonałego, którego cząsteczki mają trzy stopnie swobody, ciśnienie p wyraża się wzorem:

gdzie:

n_o - liczba cząsteczek gazu w jednostce objętości,

m - masa jednej cząsteczki,

- średnia prędkość cząsteczek.

Wzór powyższy nazywa się podstawowym równaniem teorii kinetyczno--molekularnej. Na podstawie założeń tej teorii, za pomocą parametrów określających molekularną strukturę gazu, został policzony parametr ma­kroskopowy, jakim jest ciśnienie.

Jeżeli do wzoru wprowadzić gęstość p, równą liczbowo masie jednostkowej (n₀ m), to wyrażenie na ciśnienie p przyjmie postać:

Z równania tego wynika, że ciśnienie, jakie wywiera gaz na ścianki naczy­nia, jest proporcjonalne do kwadratu średniej prędkości chaotycznego ru­chu cząsteczek tego gazu. Jest to kinetyczna interpretacja wielkości makroskopowej, jaką jest ciśnienie, za pomocą wielkości określających mikrostrukturę gazu.

Równaniem stanu gazu doskonałego jest równanie Clapeyrona, które wyraża związek między trzema parametrami stanu gazu (p, V, T).

gdzie:

V- obj. jednego mola gazu,

R - stała gazowa 8,32

T - temperatura w skali bezwzględnej.

Zgodnie z kinetyczno-molekularną teo­rią gazu doskonałego można definicję temperatury zapisać następująco:

gdzie:

E - średnia energia kinetyczna chaotycznego ruchu cząsteczek gazu.

Ze powyższego związku matematycznego wynika, że temperatura gazu jest proporcjonalna do średniej energii kinetycznej chaotycznego ruchu cząste­czek tego gazu. Jest to kinetyczna interpretacja wielkości makroskopo­wej, jaką jest temperatura, za pomocą wielkości opisujących mikrostruk­turę gazu.

Związek średniej energii kinetycznej ruchu postępowego cząsteczek gazu z wielkością makroskopową, jaką jest temperatura T można otrzy­mać z równania ciśnienia p. Po pomnożeniu obustronnie przez obję­tość jednego mola V_μ otrzymujemy:

Iloczyn n₀V_μ określa liczbę cząsteczek gazu w objętości jednego mola, a za­tem równa się liczbie Avogadra
, możemy wobec tego napisać:

Wykorzystując równanie Clapeyrona oraz równanie powyższe, otrzyma­my układ równań, w których lewe strony są sobie równe. Porównując prawe strony tych równań otrzymujemy:

stąd

Stosunek
nazywa się stała Boltzmanna. Przy jego uwzględnieniu ostatecznie wyrażenie na średnią energię kinematyczną cząsteczek gazu w funkcji temperatury ma postać:

Cząsteczki gazu doskonałego mają trzy stopnie swobody. Możemy wy­kazać, że na każdy stopień swobody cząsteczki przypada średnio taka sama energia kinetyczna, równa 1/2 kT. Jest to tzw. prawo ekwipartycji energii, jedno z podstawowych stwierdzeń klasycznej fizyki statystycznej i termodynamiki.

Właściwości makroskopowe gazu opisują zasady termodynamiki. Pierwsza zasada termodynamiki mówi, że zmiana energii wewnętrznej układu ΔU równa się sumie algebraicznej ciepła Q, przekazywanego w cza­sie procesu i wykonywanej pracy W

Wielkość Q jest dodatnia, gdy układ pobiera ciepło, ujemna - gdy oddaje. Podobnie wielkość W jest dodatnia, gdy praca jest wykonywana nad układem, ujemna - gdy układ wykonuje pracę. Jeżeli Q = 0 oraz W = 0, to ΔU = 0, czyli U = const.

Procesy adiabatyczne. Procesy adiabatyczne są to takie przemiany gazowe, które zachodzą bez wymiany ciepła z otoczeniem. Pierwsza zasada termodynamiki przyjmuje postać:

gdzie:

ΔU - wzrost lub ubytek energii wewnętrznej, zależnie od znaku W.

Energia wewnętrzna 1 mola gazu doskonałego jako funkcja temperatu­ry ma następującą postać:

dzie:

C_v - molowe ciepło właściwe gazu przy stałej objętości.

Przyrost energii wewnętrznej na skutek zmiany temperatury oblicza się przez zróżniczkowanie względem temperatury wyrażenia.

Praca, jaką wykonuje gaz przy adiabatycznym zwiększeniu objętości o do­wolnie małą wartość dV, równa się:

Biorąc powyższe pod uwagę, dla dowolnie małych zmian energii wewnętrz­nej dU, I zasadę termodynamiki dla procesów adiabatycznych można zapisać w postaci:

Wartość ciśnienia jakie wywiera gaz na ścianki naczynia, wynika z równania Clapeyrona:

Podstawiając tę wielkość do równania
i przekształcając je, otrzymamy:

Całkując otrzymane równanie w granicach zmian objętości i temperatury

otrzymuje się równanie Poissona:

lub

gdzie:

-molowe ciepło właściwe przy stałym ciśnieniu gazu

C_p - molowe ciepło właściwe przy stałym ciśnieniu gazu.

Z równania tego wynika, że przy adiabatycznej zmianie objętości gazu zachodzi zmiana jego temperatury.

Molowe ciepło właściwe przy stałym ciśnieniu gazu C_p jest większe od molowego ciepła właściwego przy stałej objętości gazu C_v o wartość pracy, jaką gaz wykonuje przy zwiększeniu objętości dla zachowania stałego ciśnienia podczas ogrzewania o jeden stopień.

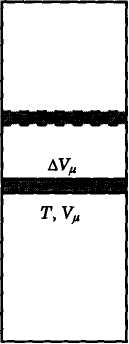
Obliczamy wartość pracy W, zakładając, że gaz jest zamknięty w naczyniu z ruchomym tłokiem, ciśnienie gazu w naczyniu wynosi p, objętość naczynia V_μ ,a temperatura gazu T.

Jeżeli gaz ogrzewamy, to jego objętość wzrośnie o ΔV_μ , czyli tłok przesuwa się o Δh. Pracę, jaką wykonał gaz, przesuwając tłok o powierzchni S na odcinku Δh, oblicza się ze wzoru:

Objętość gazu po rozprężeniu wynosi V_μ'. W związku z tym, że:

to równanie na pracę można zapisać:

Jeżeli gaz ogrzejemy o jeden stopień, to podstawiając do powyższego równania
oraz
otrzymuje się:

czyli

C_p=C_v+R

a więc

C_p>C_v

Z otrzymanej równości wynika sens fizyczny stałej gazowej. Stała ga­zowa R jest równa liczbowo pracy wykonanej przez jeden mol gazu dosko­nałego pod stałym ciśnieniem przy rozprężeniu podczas ogrzewania go o jeden stopień.

Metoda pomiaru.

W dużym naczyniu szklanym B jest gaz (w tym ćwiczeniu powietrze) pod ciśnieniem nieco wyższym od atmosfe­rycznego - równym p + p₁. Jeżeli otworzymy korek K i po chwili zamknie­my, to ciśnienie gazu w naczyniu zrówna się z ciśnieniem atmosferycznym. Proces ten zachodzi bardzo szybko, więc możemy uważać, że przy przej­ściu ze stanu I do stanu II nastąpiło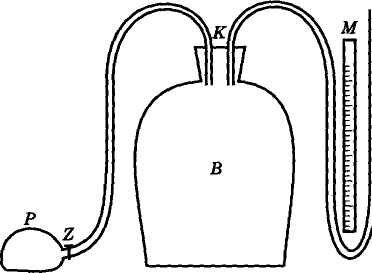
adiabatyczne rozprężenie gazu.

P — pompka

Z - zaworek

K - korek

B - pojemnik

M— manometr

Zgodnie z prawem Poissona zachodzi następująca zależność:

gdzie:

p - ciśnienie atmosferyczne,

V₁ - objętość gazu przed rozprężeniem (objętość naczynia B),

V₂ - objętość gazu po rozprężeniu.

Przy adiabatycznym rozprężeniu gaz ulega oziębieniu. Po pewnym cza­sie, na skutek wymiany ciepła z otoczeniem, temperatura gazu w naczyniu zrówna się z temperaturą otoczenia i wytworzy się nadwyżka ciśnienia p₂. Objętość nie ulega zmianie, a więc przy przejściu ze stanu II do stanu III mamy przemianę izochoryczną.

Rozpatrując stan początkowy i końcowy gazu, który poddajemy prze­mianom, a więc przejście od stanu I do III, widzimy, że jest to proces izotermiczny, ponieważ w obu stanach temperatura gazu równa się tempe­raturze otoczenia. Nadwyżka ciśnienia p₂ jest bardzo mała w porównaniu z ciśnieniem atmosferycznym, słuszne więc jest tu, z pewnym przybliże­niem, równanie Boyle'a i Mariotte'a, zapisane następująco:

Przekształcając dalej otrzymujemy:

a po logarytmowaniu:

Rozwijając ln(p + p₁) na szereg otrzymamy:

Analogicznie rozwijamy ln(p+p₂). W związku z tym, że p>p₁ oraz p>p₂, wyrazy drugiego i wyższych rzędów opuszczamy, a więc:

Nadciśnienia p₁ i p₂ można wyrazić za pomocą różnicy poziomów h₁ i h₂ cieczy w manometrze:

gdzie:

ρ-gęstość cieczy

g-przyśpieszenie ziemskie

Wzór przyjmuje więc postać:

Wykonanie pomiaru:

1. Otworzyć zaworek Z i za pomocą pompki A sprężyć powietrze w naczy­niu B. Zamknąć zaworek Z i czekać na wyrównanie temperatury między gazem a otoczeniem (poznajemy po ustaleniu wahań cieczy w manometrze). Odczytać nadciśnienie h₁ (w mm) ze skali manometru M.

2. Wyjąć korek K i po wyrównaniu się ciśnienia z ciśnieniem atmosferycz­nym natychmiast zamknąć butlę korkiem. Na skutek ogrzewania się po­wietrze w naczyniu powstaje nadciśnienie h₂, które wskazuje manometr.

3. Pomiar wykonać kilka razy (ok. 10). Ze wzoru
   obliczyć
   . Wyniki zestawić w tabelce.

Nr pomiaru	t^oC	h1	h2	h1-h2

4. Obliczyć niepewności wyniku pomiaru

Obliczanie niepewności pomiaru kappa.

Pomiar przeprowadzamy n razy (minimum 10 razy). Jest to jedno z niewielu doświadczeń, w którym do oceny niepewności wyznaczanej wielkości możemy zastosować metodę typu A. Najlepszą estymatą wartości
wielkości jest średnia arytmetycz­na uzyskanych wyników. Odchylenie standardowe średniej wyników pomiaru s(
) określa zależność:




Najlepszą estymatą niepewności standardowej wartości (
) jest odchyle­nie standardowe obliczone na podstawie powyższego wzoru. Niezależnie możemy jeszcze oszacować niepewność pojedynczego pomiaru
, stosując metodę typu B. W tym przypadku musimy założyć, że wielkości bezpośrednio mierzone czyli h₁ i h₂ znajdują się w określonym przedziale o szerokościach połówkowych odpowiednio Δh₁ i Δh₂. Jeżeli założymy, że rozkład prawdopodobieństwa znalezienia tych wartości w określonych przedziałach jest rozkładem prostokątnym, niepewność standardowa war­tości h₁ i h₂ wyniesie odpowiednio:


i



zatem złożoną niepewność standardową wielkości
obliczymy ze wzoru:




co po podstawieniu pochodnych cząstkowych daje wyrażenie:




po przekształceniu i skorzystaniu z faktu, że Δh₁= Δh₂= Δh otrzymujemy:




---