Neuron

Jest Podstawowym elementem składowym sieci neuronowej.

Jego schemat został opracowany przez McCullocha i Pittsa w 1943 roku i oparty został na budowie biologicznej komórki nerwowej .

X - wejścia

W - wagi

+ - sumator

S - sumaryczne pobudzanie neuronu

F(s) - funkcja aktywacji

Y - wyjscie

Jego działanie jest następujące:

do wejść doprowadzane są sygnały dochodzące z wejść sieci lub neuronów warstwy poprzedniej. Każdy sygnał mnożony jest przez odpowiadającą mu wartość liczbową zwaną wagą. Wpływa ona na percepcję danego sygnału wejściowego i jego udział w tworzeniu sygnału wyjściowego przez neuron. Waga może być pobudzająca - dodatnia lub opóźniająca - ujemna; jeżeli nie ma połączenia między neuronami to waga jest równa zero. Zsumowane iloczyny sygnałów i wag stanowią argument funkcji aktywacji neuronu.

Funkcja aktywacji:

Ma kluczowe znaczenie dla funkcjonowania neuronu. To funkcja wg. Której obliczana jest wartość wyjścia neuronów sieci neuronowej

Funkcja aktywacji przybiera jedną z trzech postaci:

• liniowa ( y = e, najprostszy możliwy przypadek),

• nieliniowa:

• jednobiegunowa (unipolarna), np. funkcja sigmoidalna,

• dwubiegunowa (bipolarna), np. tangens hiperboliczny,

• ciągła lub nieciągła (np. element progowy).

• skoku jednostkowego tzw. funkcja progowa

charakterystyki sigmoidalnych (nieliniowych?) funkcji aktywacji:

funkcja aktywacji liniowa i skoku jednostkowego:

Zbiór uczący:

To zbiór takich danych, które w miarę dokładnie charakteryzują dany problem.

Jednorazowa porcja danych nazywana jest wektorem uczącym.

W jego skład wchodzą:

- wektor wejściowy - te dane wejściowe które podawane są na wejściu sieci

- wektor wyjściowy - dane oczekiwane, jakie sieć powinna wygenerować na wyjściach

Współczynnik uczenia sieci ang. Learning rate

Odpowiedzialny jest za sposób modyfikacji wag neuronów.
Przyjmuje przeważnie wartości (0,1)

- mały - powolne uczenie sieci ale też większą precyzyjność dokonywanych zmian

- duży - powoduje gwałtowne zmiany parametrów sieci

Adaptacyjny współczynnik uczenia: Jego wartość zmienia się (w czasie uczenia sieci) zależnie od tego, jak uczy się sieć

W zależności od sposobu połączenia neuronów sieci dzieli my na:

Jednokierunkowe - są to sieci, w których nie występują sprzężenia zwrotne, czyli dany sygnał przechodzi przez dany neutron tylko jeden raz - w jednym kierunku od wejścia do wyjścia. Metody uczenia sieci są proste i łatwe do realizacji w praktyce - zwykle uczenie odbywa się z nauczycielem

Rekurencyjne

W sieciach rekurencyjnych istnieją sprzężenia zwrotne między wejściem, a wyjściem. Zależności dynamiczne jakie panują w sieci są widoczne na każdym etapie działania. Zmiana stanu jednego neuronu przenosi się przez masowe sprzężenie zwrotne na całą sieć, wywołując stan przejściowy, kończący się określonym stanem ustalonym, na ogół innym niż stan poprzedni

- dopuszcza się istnienie sprzężeń zwrotnych tzn. wyjścia neuronów mogą być połączone z wejściami neuronów tej samej warstwy lub warstw pośrednich

- informacja oscyluje między warstwami lub w obrębie warstw aż do spełnienia pewnego kryterium zbieżności i dopiero wtedy jest przekazywana na wyjście sieci

Modele sieci z rekurencją:

-Hamminga

-Hopfielda

-typu BAM

-Elmana

Siec Hopfielda:

Właściwości:

- sieć ze sprzężeniem zwrotnym: wejścia to wyjścia innych neuronów

- brak własnego sprzężenia zwrotnego

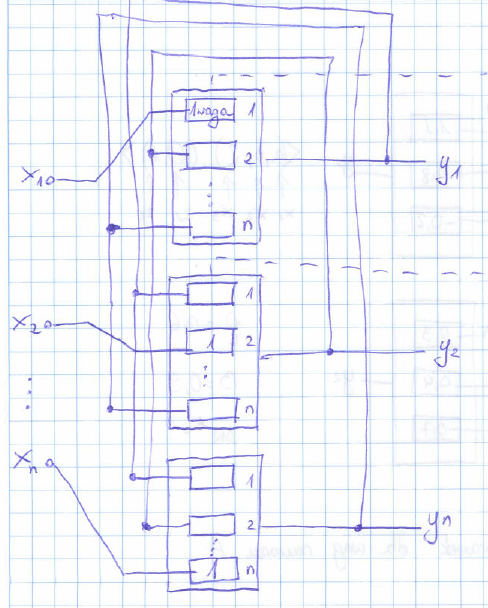
- symetryczne wagi

Tryb pracy:

- uczenia i odtwarzania

To pamięć autoasocjacyjna:

Jeśli w 2 kolejnych krokach na wyjściu wystąpi ten sam zestaw wartości to oznacza że sieć znalazła rozwiązanie

Uczenie (trening) sieci neuronowej do pełnienia funkcji pamięci asocjacyjnej ma za zadanie taki dobór wag Wij poszczególnych neuronów, aby na etapie odtwarzania sieć była zdolna odnaleźć zbiór danych, najbliższy w sensie miar Hamminga, wektorowi testującemu.

Pamięć asocjacyjna ma własności korekcyjne. Przy prezentacji próbki testującej różniącej się pewną liczbą bitów na nieskończonych pozycjach wektora, siec neuronowa jest w stanie dokonać korekcji tych bitów i zakończyć proces klasyfikacji we właściwym atraktorze.

Sieć Hamminga:

jest wyspecjalizowaną strukturą pamięci heteroasocjacyjnej

Heteroasoscjacja - sieć zapamiętuje i kojarzy pary obrazów i nawet

zniekształcony obraz wejściowy może wywołać właściwą heteroasocjację

na wyjściu (heteroasocjacja obejmuje problem klasyfikacji)

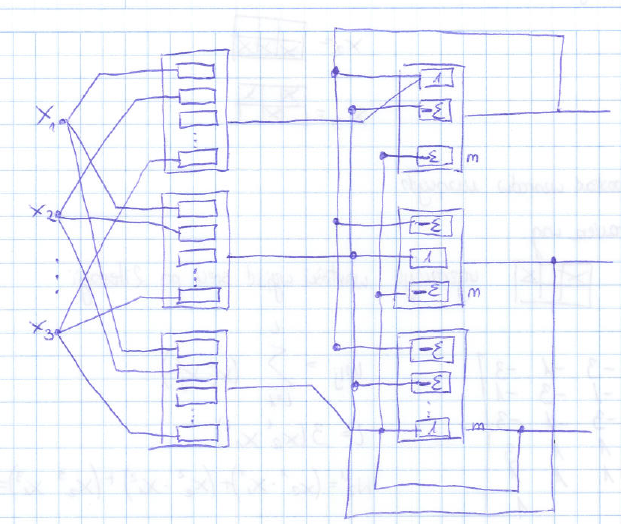
Struktura trójwarstwowa:

• warstwa pierwsza:

• jednokierunkowa z przepływem sygnałów od wejścia do wyjścia

• warstwa druga:

• MAXNET - neurony połączone sprzężeniem zwrotnym każdy z każdym

• ISTNIEJE NIEZEROWE SPRZĘŻENIE NEURONU Z WŁASNYM WYJŚCIEM

• wagi neuronu w warstwie MAXNET są stałe

• warstwa trzecia: jednokierunkowa

W działaniu omawianej sieci można wyróżnić trzy fazy.

Faza I - podawany jest na wejście sieci N-elementowy wektor x. Po jego prezentacji generowane sygnały inicjujące stan początkowy neuronów warstwy MAXNET'u.

Faza II - sygnały inicjujące działanie MAXNET'u są usuwane i rozpoczyna się proces iteracyjny w warstwie MAXNET'u, inicjowany stanem początkowym. Proces iteracyjny trwa do chwili, aż wszystkie neurony z wyjątkiem jednego osiągną stan zerowy. Neuron o niezerowym sygnale wyjściowym (zwycięzca) reprezentuje klasę, do której należy wektor wejściowy.

Faza III - neuron zwycięzca wytwarza na wyjściu sieci odpowiedź stanowiącą wektor y, skojarzony z wektorem pobudzającym x.

Sieci jednowarstwowe:

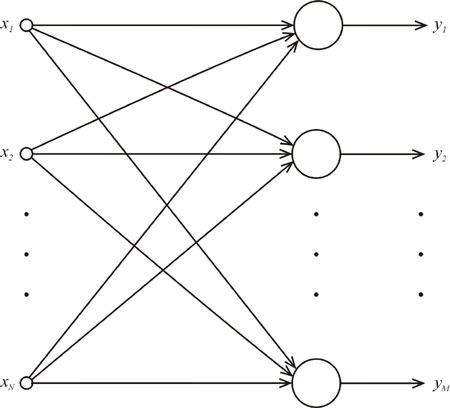
W sieci jednokierunkowej jednowarstwowej (rys.) neurony są ułożone w jednej warstwie, zasilanej z węzłów wejściowych. Połączenie węzłów wejściowych z neuronami warstwy wyjściowej jest zwykle typu każdy z każdym tzn. każdy węzeł z każdym neuronem. Przepływ sygnałów występuje w jednym kierunku, od wejścia do wyjścia.

Węzły wejściowe nie tworzą warstwy neuronów, gdyż nie zachodzi w nich żaden proces obliczeniowy.

Sieci wielowarstwowe:

Cechą charakterystyczną sieci jednokierunkowych wielowarstwowych jest występowanie, co najmniej jednej warstwy ukrytej neuronów, która pośredniczy w przekazywaniu sygnałów między węzłami wejściowymi, a warstwą wyjściową (rys.).

Sygnały wejściowe są podawane na pierwszą warstwę ukrytą neuronów, a te z kolei stanowią sygnały źródłowe dla kolejnej warstwy. W sieci tej występują połączenia pełne między warstwami.

Uczenie perceptronu wielowarstwowego odbywa się zwykle z nauczycielem.

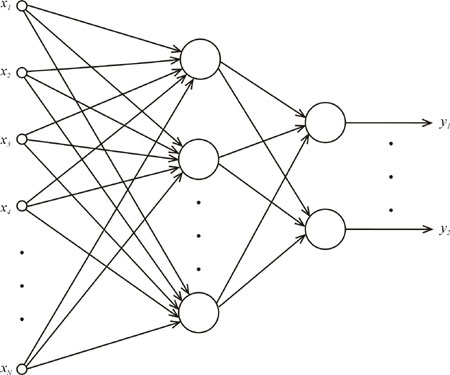
Sieci jednokierunkowe wielowarstwowe często wykorzystują nieliniową funkcję aktywacji typu sigmoidalnego

Ponieważ sieć wielowarstwowa o trzech warstwach realizuje odwzorowanie dowolnej przestrzeni X w dowolną przestrzeń Y w postaci X->Y, wynika więc z tego, że nasza sieć powinna być zbudowana z przynajmniej trzech warstw

Perceptron

[sieć jednokierunkowa złożona z neuronów o nieliniowej (unipolarnej lub bipolarnej) funkcji aktywacji.]

Jednym z podstawowych modeli sieci jednokierunkowych jest perceptron przedstawiony na rysunku poniżej. Perceptron zbudowany jest z N neuronów wejściowych i M neuronów wyjściowych. Elementy zarówno wejścia jak wyjścia perceptronu przyjmują wartości binarne, tzn. należą do zbioru {0,1}.

Zadaniem perceptronu jest odwzorowanie zadanego zbioru wektorów wejściowych na zadany zbiór wektorów wyjściowych. W związku z tym zbiór danych uczących składa się z par (xⁱ, yⁱ), których = 1,…,s, w których xⁱ jest n elementowym wektorem wejściowym, a yⁱ skojarzonym z nim m elementowym wektorem wyjściowym.

Każdy z neuronów y_k, k = 1 ÷ m warstwy wyjściowej oblicza swoją wartość według poniższej zasady:

Proces nauki perceptronu polega na stopniowej modyfikacji wag łączących neurony wejściowe z wyjściowymi w taki sposób, żeby po jego zakończeniu podanie na wejściu któregokolwiek z wektorów xⁱ,i = 1÷s powodowało wygenerowanie na wyjściu wektora yⁱ.

---