moduł szt sprężystych drgań obr, Budownictwo PG, Semestr 2, Fizyka, Laborki Fizyka, Laborki - chomik, Laboratorium (metalbob), Fizyka Sprawozdania, Fiza labory

CEL ĆWICZENIA

Celem ćwiczenia jest wyznaczenie występującego w prawie Hook ' a modułu sztywności przez pomiar okresu sprężystych drgań obrotowych .

CZĘŚĆ TEORETYCZNA

Ciało nazywamy sprężystym , jeżeli odkształcenia , wywołane działającymi na nie siłami ,znikają zupełnie po usunięciu tych sił. Każde ciało zbudowane jest z atomów lub cząsteczek, między którymi działają siły nazywane siłami międzycząsteczkowymi. W ciałach stałych siły te są na tyle duże, że cząsteczki są uporządkowane i tworzą regularną strukturę przestrzenną ,nazywaną siecią krystaliczną . Każda cząsteczka nazwana węzłem sieciowym ma swoje położenie równowagi, wokół, którego wykonuje niewielkie, chaotyczne drgania . Powstanie stanu równowagi trwałej, wynika z faktu, że między kolejnymi dwiema cząsteczkami występują dwojakiego rodzaju siły :przyciągania oraz odpychania. Siły odpychania rosną zawsze znacznie bardziej wraz ze zbliżaniem się cząsteczek niż sily przyciągania.

Siła przyciągania opisana jest wzorem :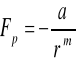

Siła odpychania opisana jest wzorem :
,

stałe a i b zależą od budowy znajdującej się w wężle sieci cząsteczki oraz rodzaju sił wiązania .

Każda cząsteczka w krysztale ma określoną energię potencjalną oraz kinetyczną .

Rozróżniamy cztery rodzaje wiązań atomów lub cząsteczek w ciałach stałych :

1. Jonowe (heteropolarne lub walencyjne) - które powstaje na skutek przyciągania się na przemian rozmieszczonych różnoimiennych jonów np . w kryształach NaCl , KCl .

2.Atomowe (homepolarne lub kowalencyjne) - które jest wynikiem tego , że pewne sąsiadujące ze sobą atomy zawierają wspólne dwa elektrony np . diament , grafit , krzem , german .

3.Metaliczne , które wynika z tego ,że istnieje grupa elektronów wspólna wszystkim atomom kryształu . Nazywamy je grupą lub "chmurą" elektronów swobodnych .

4.Van der Waalsa (cząsteczkowe) - w kryształach o tym typie wiązania w węzłach sieci znajdują się obojętne cząsteczki .Siły oddziaływania między nimi powstają na skutek oddziaływania ich wewnętrznych pól elektrycznych oraz oddziaływania drgających ładunków elektrycznych .

Siły działające na ciało wywołują ich odkształcenia . Wszelkie odkształcenia można sprowadzić do trzech głównych rodzajów odkształceń :

1.Odkształcenie jednostronne występuje wtedy , gdy siły działają na dwie przeciwległe ścianki ciała prostopadle do nich .

2.Odkształcenie wszechstronne występuje wtedy ,gdy na każdy element powierzchni ciała działa siła do niego prostopadła .

3.Ścinanie następuje wtedy , gdy działające siły są styczne do powierzchni ciała .

Naprężeniem nazywamy wektor o wartości równej stosunkowi wartości siły do powierzchni , na którą ona działa , o kierunku i zwrocie zgodnym z kierunkiem siły :

Jednostką naprężenia jest takie naprężenie , jakie wywołuje jednostkowa siła działając na jednostkową powierzchnię .W układzie SI jednostką naprężenia jest paskal (P) :jest to naprężenie jakie wywołuje siła jednego niutona działając na powierzchnię jednego metra kwadratowego .

Prawo Hooke'a formułuje zależność między naprężeniem a odkształceniem :

Jeżęli naprężenia w ciele są dostatecznie małe , to wywołane przez nie odkształcenie względne są do nich wprost proporcjonalne .

;
;
.

Współczynniki proporcjonalności 1/E , 1/K , 1/G nazywamy współczynnikami sprężystości , a ich odwrotności modułami :

E - moduł Younga ; K - moduł ściśliwości ; G - moduł sztywności . Są to stałe materiałowe.

Pośród metali największe wartości modułu sztywności ma stal G = 79500 MPa , a najmniejsze

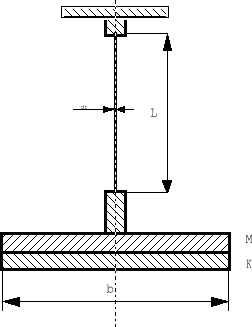
aluminium G = 26500 MPa . Stałą materiałową zwaną modułem sztywności G możemy wyznaczyć poprzez pomiar okresu sprężystych drgań obrotowych układu przedstawionego na rysunku 1 .

WZÓR KOŃCOWY:

a / forma podręcznikowa