Przykładowe zadania
Zadanie 1
Oszacuj modelu popytu na produkt ABC w zależności od ceny tego produktu, gdzie Y - popyt (w tys. sztuk), X - cena (w zł). Na podstawie 10 obserwacji otrzymano następujące wyniki:
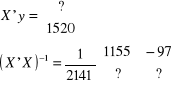
SKR = 7,732,
OSK = 1881,6
Oszacuj parametru modelu liniowego, oceń dopasowanie modelu do danych empirycznych oraz zbadaj istotność zmiennej objaśniającej na poziomie istotności 0,05.
Zadanie 2
Uzyskano oszacowanie formy liniowej zależności popytu (P) względem dochodów (D) oraz cen (C):
ln P = 0,0107 + 1,2 lnD - 0,3 lnC, R2 = 0,981; s= 0,0021,
(14,5) (1,4) (6,7)
a) Model oryginalny ma postać….
b) Elastyczność dochodowa popytu wynosi …………..
c) Elastyczność cenowa ……
d) Gdy dochody wzrosną o 1%, popyt przypuszczalnie………
e) gdy ceny wzrosną o 1% to popyt przypuszczalnie zmaleje………
f) Jeśli dochody i ceny wzrosną o 1 % to popyt wzrośnie o ………..
g) Model jest/nie jest poprawny, gdyż
Pod parametrami podano empiryczne statystyki t Studenta
Zadanie 3
Przypuszcza się, że wydajność pracy WY (WY = PR/ZA; PR - produkcja, ZA - zatrudnienie) w następujący sposób zależy od technicznego uzbrojenia pracy TUP (TUP = MA/ZA, MA - majątek):
• przy jednostkowym technicznym uzbrojeniu pracy wydajność wynosi 12,3 tys. zł;
• ze wzrostem technicznego uzbrojenia pracy o 1%, wydajność wzrasta o 0,8%.
a) model wydajności względem technicznego uzbrojenia pracy jest
b) a jego wzór ma postać
c) model produkcji względem zatrudnienia i majątku jest
d) a jego wzór ma postać
e) przy jednostkowych nakładach zatrudnienia i majątku oczekiwana wielkość produkcji wynosi…
f) zbadaj efekt skali produkcji
Zadanie 4
Do następujących oszacowań form zlinearyzowanych podaj postać modelu oryginalnego:
lnY = 0,65 + 0,03X
Y = 2,34 + 3,45Z (Z=1/X)
lnY = 2,34 + 0,83lnX
Zadanie 5
Podaj interpretację współczynnika kierunkowego następujących modeli:
