POMIAR ŁADUNKU I POJEMNOŚCI ELEKTRYCZNEJ KONDENSATORA.

1. CEL ĆWICZENIA.

Pojemność kondensatora - stosunek ładunku na jednej z okładzin do napięcia panującego między okładzinami:

C = Q / U [ 1 F ] = [ 1 C / 1 V ]

Pojemność zależy od wymiarów geometrycznych kondensatora oraz od stałej dielektrycznej ośrodka wypełniającego przestrzeń między okładzinami:

C = _  S / d

gdzie:

₀ - przenikalność dielektryczna próżni = 1/36 * 10^-9 As / Vm

 - stała dielektryczna ośrodka

S - powierzchnia okładzin

d - odległość między okładzinami

Kondensatory można łączyć w układach szeregowo lub równolegle.

2. WYZNACZANIE ŁADUNKU KONDENSATORA METODĄ GRAFICZNEGO CAŁKOWANIA.

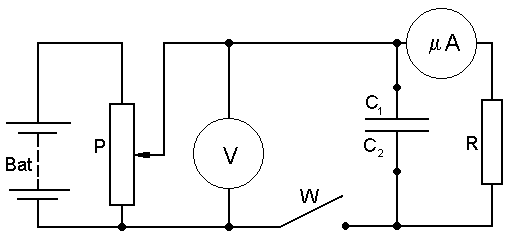
Układ do wyznaczania krzywej rozładowania kondensatora.

R - duża rezystancja zapobiegająca zbyt szybkiemu rozładowaniu kondensatora

Ładowanie odbywa się przy napięciu ustawionym na 100V. Rozładowanie kondensatora przeprowadza się przy otwartym wyłączniku W.

Na podstawie pomiarów sporządza się wykres zależności I = f (t).

a/ dla kondensatora C₁:

L.p.	t	I
		s	A
1	0	46
2	2	38
3	4	32
4	6	27
5	8	22
6	10	19
7	12	16
8	14	10
9	16	9
10	18	7
11	20	6
12	22	4
13	24	3
14	26	2
15	28	2

Całkowity ładunek zgromadzony na kondensatorze jest równy:

Q = ( I₀ + I₁ ) / 2 * 2s + ( I₁ + I₂ ) / 2 * 2s + … + ( I₁₄ + I₁₅ ) / 2 * 2s

Q = 438 C

Błąd pomiaru ładunku wynosi:

Q = I * t_n

Q = 5,6 * 10^-9 C

gdzie:

2s - przedział czasowy, co który dokonywano kolejnych pomiarów

I - błąd pomiarowy mikroamperomierza = 2 A

t_n - czas rozładowania kondensatora = 28 s

Zatem pojemność badanego kondensatora wynosi:

C₁ = Q / U  Q / U

C₁ = 4,38 F  0,56 F

b/ dla kondensatora C₂:

L.p.	t	I
		s	A
1	0	46
2	2	44
3	4	28
4	6	19
5	8	16
6	10	12
7	12	10
8	14	6
9	16	6
10	18	4
11	20	3
12	22	2

Całkowity ładunek zgromadzony na kondensatorze jest równy:

Q = ( I₀ + I₁ ) / 2 * 2s + ( I₁ + I₂ ) / 2 * 2s + … + ( I₁₁ + I₁₂ ) / 2 * 2s

Q = 344 C

Błąd pomiaru ładunku wynosi:

Q = I * t_n

Q = 4,4 * 10^-9 C

I = 2 A

t_n = 22 s

Pojemność badanego kondensatora wynosi:

C₂ = Q / U  Q / U

C₂ = 3,44 F  0,44 F

c/ dla połączenia równoległego dwóch kondensatorów:

L.p.	t	I
		s	A
1	0	46
2	2	42
3	4	37
4	6	34
5	8	28
6	10	26
7	12	22
8	14	20
9	16	18
10	18	16
11	20	14
12	22	12
13	24	11
14	26	10
15	28	9
16	30	8
17	32	7
18	34	6
19	36	5
20	38	5
21	40	4
22	42	4
23	44	3
24	46	3
25	48	2
26	50	2

Ładunek zgromadzony na kondensatorach jest równy:

Q = ( I₀ + I₁ ) / 2 * 2s + ( I₁ + I₂ ) / 2 * 2s + … + ( I₂₅ + I₂₆ ) / 2 * 2s

Q = 782 C

Błąd pomiaru ładunku wynosi:

Q = I * t_n

Q = 1 * 10^-9 C

I = 2 A

t_n = 50 s

Pojemność badanych kondensatorów wynosi:

C₂ = Q / U  Q / U

C₂ = 7,82 F  0,01 F

3. WNIOSKI KOŃCOWE.

W badanym układzie potwierdza się prawo mówiące, że pojemność zastępcza kondensatorów połączonych równolegle jest równa sumie algebraicznej wszystkich kondensatorów wchodzących w skład tego układu. W tym przypadku było to:

C_z = C₁ + C₂

7,82 F = 4,38 F + 3,44 F

Na podstawie uzyskanych wyników można także stwierdzić, iż im mniejsza jest pojemność kondensatora, tym szybszy jest czas jego rozładowania t_n.

Błędy pomiarowe występujące w tym ćwiczeniu wynikają z niedokładności analogowych mierników użytych do pomiarów ( dla woltomierza U = 0,75 V, dla mikroamperomierza I = 2 A ) i bezwładności odczytu prądu w kolejnych jednostkach czasu mierzonego stoperem.

---