Temperatura cieczy t [C]	czas	Gęstość cieczy	Lepkość η	Temperatura T [K]	1/T	lnη
20	188,6	1,2347	168,2	293,15	0,00341	5,125
30	105	1,1664	94,57	303,15	0,00329	4,549
40	58,6	1,1202	53,12	313,15	0,00319	3,972
50	37,5	1,1136	34,03	323,15	0,00309	3,527
60	24,6	1,1082	22,34	333,15	0,00300	3,106

K = 0,12908 [mPa cm³] q_k = 8,144 [g/cm³]

Nr	X	Y	xy	X^2
1	0,00341	5,125	0,0174	0,0000116
2	0,00329	4,549	0,0149	0,0000108
3	0,00319	3,972	0,0126	0,0000101
4	0,00309	3,527	0,0108	0,0000095
5	0,00300	3,106	0,0093	0,0000090

Σx = 0,01598 (Σx)² = 0,00025536

Σy = 20,279

Σxy = 0,065

Σx² = 0,000051

1. Z wykresu lnη = f(1/T) wyznaczam graficznie wartości stałych A i ΔE_lepk wiedząc, że współczynnik kierunkowy b uzyskanej prostej jest równy ΔE_lepk / R , a punkt przecięcia prostej z osią rzędnych jest równy lnA.

a=y₁-bx₁ = 5,125 - 480⋅0,00341 = 3,4882

[J/K⋅mol]

a = lnA

lnA = 3,4882

A = e^3,4882

A = 32,72

2. Z wykresu lnη = f(1/T) wyznaczam metodą najmniejszych kwadratów wartości stałych A i ΔE_lepk , pamiętając, że y_i = lnη a x_i = 1/T

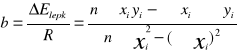
b= -26155

217 452,67 [J/K⋅mol]

a=lnA

lnA = 4,086

A = e^4,086

A=59,5

---