ANALIZA SZEREGÓW CZASOWYCH - metoda pasywna prognozowania, analizujemy jak zjawisko kształtuje się w czasie, nie rozpatrujemy przyczyn takiego zachowania.
1. SKŁADOWE SZEREGÓW CZASOWYCH
Systematyczne:
Stały przeciętny poziom (CONST))
Tendencja rozwojowa - trend
Wahania sezonowe : multiplikatywne i addytywne
Cykle koniunkturalne
Niesystematyczne:
Wahania przypadkowe - nasza zmora i przekleństwo
Uwaga!
Aby właściwiej rozpoznać składowe szeregu czasowego, musimy dysponować odpowiedniej długości szeregami czasowymi.
METODY NAIWNE
Błądzenie losowe ![]()
(+ ε)
Szereg z tendencją rozwojową
![]()
![]()
![]()
lub d) ![]()
![]()
, 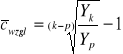
Szereg czasowy z wahaniami sezonowymi
Np. dla kwartalnych wahań sezonowych ![]()
Uwagi:
Prognozy mają charakter krótkookresowy .
Prognosta wykorzystuje zasadę status quo.
Nie zawsze da się je zastosować, ale mogą być wykorzystywane w przypadku krótkich szeregów czasowych, czyli wtedy kiedy innych metod nie można zastosować.
Oceny dopuszczalności prognozy dokonuje się na podstawie błędów prognozy ex post.
Jeżeli w szeregu czasowym zmiennej oprócz składowych systematycznych występują stosunkowo duże wahania przypadkowe, to prognozy wyznaczone przy użyciu metod naiwnych będą obarczone dużymi błędami.
3. METODA ŚREDNIEJ RUCHOMEJ
Prosta średnia arytmetyczna i geometryczna
![]()
****![]()
Średnia ruchoma prosta
![]()
gdzie: k - stała wygładzania
Średnia ruchoma ważona
![]()
gdzie: 0 < w1 < w2 < wk <=1
Uwagi:
Prognosta wykorzystuje zasadę status quo.
Jeżeli w szeregu czasowym zmiennej oprócz składowych systematycznych występują stosunkowo duże wahania przypadkowe, to prognozy wyznaczone przy użyciu metod naiwnych będą obarczone dużymi błędami. W celu poprawienia dokładności konstruowanych prognoz można zastosować średnie ruchome.
Stosowane zwykle wtedy kiedy w szeregu występuje stały przeciętny poziom i wahania przypadkowe. Nie stosuje się dla tendencji rozwojowych i wahań sezonowych. (Wyjątek: notowania giełdowe).
Mogą być wykorzystywane w przypadku krótkich szeregów czasowych, czyli wtedy kiedy innych metod nie można zastosować.
Oceny dopuszczalności prognozy dokonuje się na podstawie błędów prognozy ex post.
4. BŁĘDY PROGNOZY EX POST
Błąd bezwzględny i błąd względny
![]()
, ![]()
Średni bezwzględny błąd prognozy w przedziale weryfikacji (t należy do przedziału {n+1, ...., T} )
Średni względny błąd prognozy Q w przedziale weryfikacji (t należy do przedziału {n+1, ...., T} )
![]()
Średni kwadratowy błąd prognozy (s*)
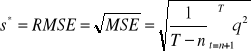
Analiza szeregów czasowych
3
MAE (MAD) mean absolute error/deviation.
Średnie odchylenie +/- wartości rzeczywistej od prognozy, wyrażone w jednostkach.
****Przykłady wag:
a)liniowe:
![]()
b) harmoniczne:
![]()
OZNACZENIA
Przyjmijmy, ze pierwsza prognoza wygasła w przedziale weryfikacji prognoz jest wyznaczona na okres t=n+1, zaś ostatnia na okres T
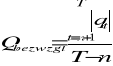
MAPE mean absolute percent(age) error
Średni błąd prognozy mierzony w procentach wartości rzeczywistej, często mnożony przez 100%, pozbawiony jednostek.
MSE - mean square(d) error.
RMSE - root of mean square(d) error.
Czasami prognosta woli się pomylić częściej, ale nieznacznie, niż rzadko, ale za to bardzo istotnie. Aby podkreślić występowanie tych dużych błędów podnosi je do kwadratu i dopiero te wartości wykorzystuje by liczyć średnie błędy.
Ponieważ MSE wyrażony jest w jednostkach do kwadratu, liczymy RMSE wyrażony w jednostkach. MSE i RMSE najczęściej wykorzystywane są w zadaniach optymalizacyjnych.
Wyszukiwarka
Podobne podstrony:
analiza struktury zad, Płyta farmacja Bydgoszcz, statystyka, pozostałe
Analiza regresji w Excelu, Płyta farmacja Bydgoszcz, statystyka, pozostałe
Analiza regresji między dwiema zmiennymi, Płyta farmacja Bydgoszcz, statystyka, pozostałe
Analiza struktur, Płyta farmacja Bydgoszcz, statystyka, pozostałe
Parametry stosowane w statystyce opisowej, Płyta farmacja Bydgoszcz, statystyka, pozostałe
Korelacje rang - ściąga, Płyta farmacja Bydgoszcz, statystyka, pozostałe
estymacja wzory, Płyta farmacja Bydgoszcz, statystyka, pozostałe
SWD, Płyta farmacja Bydgoszcz, statystyka, pozostałe
(2461) stat mat 01, Płyta farmacja Bydgoszcz, statystyka, pozostałe
więcej podobnych podstron