OBLICZANIE CIĄGU POLIGONOWEGO ZAMKNIĘTEGO I OTWARTEGO

Ciąg poligonowy

Ciąg sytuacyjny, jako podstawowa metoda zagęszczania osnowy szczegółowej, powstaje przez połączenie wybranych punktów linią łamaną. Włączenie do ciągu punktów osnowy państwowej powoduje, że ciąg ten zawiera elementy dowiązania i może być obliczony w państwowym układzie współrzędnych. Rozmieszczenie obranych w terenie punktów decyduje o kształcie ciągu. Rozróżnia się zatem ciągi sytuacyjne zamknięte oraz ciągi dowiązane otwarte.

Zgodnie z przepisami instrukcji G-4 zarówno długości boków, jak i samych ciągów są ograniczone, tak więc długość ciągu sytuacyjnego nie powinna przekraczać 2000 m, zaś długości boków powinny się mieścić w granicach od 50 do 350 m, przy czym stosunek boków przyległych nie może być mniejszy niż 1:4. Punkty ciągu sytuacyjnego muszą być tak dobrane, aby zapewnić bezpośrednią ich widoczność z sąsiednich punktów i dogodny pomiar w terenie oraz maksymalną nienaruszalność znaków.

Punkty osnowy pomiarowej należy w terenie stabilizować słupkami kamiennymi lub betonowymi, palikami, rurkami, za pomocą bolców lub trzpieni metalowych. Wszystkie długości boków ciągów sytuacyjnych trzeba mierzyć dwukrotnie. Pomiar boków należy wykonać metodami bezpośrednimi lub pośrednimi z taką dokładnością, aby różnica dwukrotnego pomiaru była nie większa niż wartość di określona z zależności:

di = Hi

gdzie: u = 0,0059 - współczynnik błędów przypadkowych pomiaru długości,
/ - długość mierzonego boku w metrach.

Pomiar kątów w ciągach sytuacyjnych wykonuje się instrumentem gwarantującym uzyskanie średniego błędu pomiaru kąta mo < 30 (90°^c).

Kąty wierzchołkowe mierzy się w jednej serii, ale różnica pomiaru kąta w dwóch położeniach lunety nie powinna być większa od podwójnej wartości m₀.

CIĄG POLIGONOWY ZAMKNIĘTY

Obliczenie i wyrównanie zamkniętego ciągu sytuacyjnego, dowiązanego do dwóch punktów

1. Wpisanie danych do formularza obliczeń.

Do formularza obliczeń wpisuje się pomierzone kąty wierzchołkowe, pomierzone długości boków oraz współrzędne punktu dowiązania ... i azymut początkowy α_1-2.

2.0bliczenie teoretycznej sumy kątów

Dla wieloboku zamkniętego o n kątach teoretyczna suma kątów wewnętrznych wynosi:

Σ_βt = (n-2)·180°

Σ_βt =(5-2) ·180°

Σ_βt = 540°00'00"

3. Obliczenie praktycznej sumy kątów

Praktyczną sumę kątów Σ_βt otrzymuje się sumując pomierzone kąty.

Σ_βt = 540^o00'l0"

4.Obliczenie odchyłki kątowej ciągu

Odchyłka kątowa ciągu f_β w ciągach poligonowych jest to różnica między sumą pomierzonych w ciągu kątów Σ_βp a sumą teoretyczną Σ_βt, zatem:

f_β=Σ_βp- Σ_βt

f_β = 540°00 10"-540° 00'00"

f_β=10"

f_β=10"<f_βmax = 30"

Wartość odchyłki kątowej f_β nie powinna przekraczać odchyłki maksymalnej f_{β max}

obliczonej z zależności:

f_βmax= mo

gdzie: mo - średni błąd pomiaru kąta,

n_K - liczba kątów zmierzonych w ciągu.

5.0bliczenie poprawek do pomierzonych kątów

Obliczona odchyłka kątowa powinna f_β być rozdzielona na zmierzone kąty. Każdy pomierzony kąt otrzyma poprawkę V_β

V_β =-f/n_k

Obliczone dla omawianego przykładu poprawki V_β do pomierzonych kątów wynoszą

V_β=-10/5=2

6 Obliczenie azymutów ciągu poligonowego zamkniętego

Obliczenie azymutów boków ciągu sytuacyjnego rozpoczyna się od obliczenia ze współrzędnych azymutu boku łączącego punkty o znanych współrzędnych. Oznaczając obliczony azymut boku opartego na punktach nawiązania przez Aab, azymuty kolejnych boków oblicza się w oparciu o wyrównane kąty wierzchołkowe. W zależności od przyjętego kierunku obliczeń przyjmuje się określenie: „kąty lewe" lub „kąty prawe". Jako kąty lewe przyjmuje się kąty położone po lewej stronie ciągu, idąc w przyjętym kierunku obliczeń. Dla kątów prawych azymut kolejnego boku wynosi:

A_i = A_i.₁ + 180°-β_i

a dla kątów lewych:

A_i= A_i.₁-180°+ β_i

7 Obliczenie przyrostów współrzędnych boków ciągu

Przyrosty Δxi i Δyi współrzędnych boku Ii oblicza się z zależności:

Δxi = Ii cos Ai Δyi = Ii sin Ai

gdzie li- długość boku Ai- azymut boku W zależności od wartości azymutu boku obliczone wartości przyrostów opatrzone będą odpowiednimi znakami.

8. Obliczanie praktycznej sumy kątów:

Praktyczną sumę przyrostów otrzymuje się sumując obliczone przyrosty Δx i Δy

9 Teoretyczna suma przyrostów w ciągu zamkniętym wynosi:

Σ_t Δx=0

Σ_t Δy=0

10Obliczenie odchyłek sum przyrostów

Różnice pomiędzy obliczonymi a teoretycznymi sumami przyrostów noszą nazwy odchyłek

przyrostów i są oznaczone przez f_x i f_y

f_x= Σ_pΔx- Σ_t Δx

f_y= Σ_pΔy- Σ_t Δy

l1 Obliczenie odchyłki liniowej

Odchyłkę liniową ciągu f_l oblicza się ze wzoru:

Odchyłka liniowa ciągu powinna być mniejsza od odchyłki maksymalnej:

flmax = 0.20 [m]

fi ^< f_lmax

l2 Obliczenie poprawek i wyrównanie przyrostów do sumy teoretycznej

1. W obliczeniach ciągów sytuacyjnych odchyłki przyrostów rozdziela się proporcjonalnie do długości boków ciągu, stosując zależność:

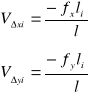
gdzie: - V_Δxi , V_Δyi poprawki do obliczonych przyrostów współrzędnych,

l_i - długość i-tego boku ciągu,

Σl - suma długości boków w ciągu.

Suma przyrostów skorygowanych o obliczone poprawki V_xi i V_yi równa jest sumie teoretycznej. Wartości poprawek zaokrągla się do wartości odpowiadającej dokładności pomiaru długości boków ciągu.

130bliczenie współrzędnych ciągu

2. Współrzędne punktów ciągu sytuacyjnego oblicza się w ten sposób, że do znanych współrzędnych punktu poprzedniego w ciągu dodaje się przyrosty Δx i Δy, otrzymując współrzędne kolejnych punktów:

x_i = x_i-1 + Δxi

y_i = y_i-1+ Δy_i

CIĄG POLIGONOWY OTWARTY

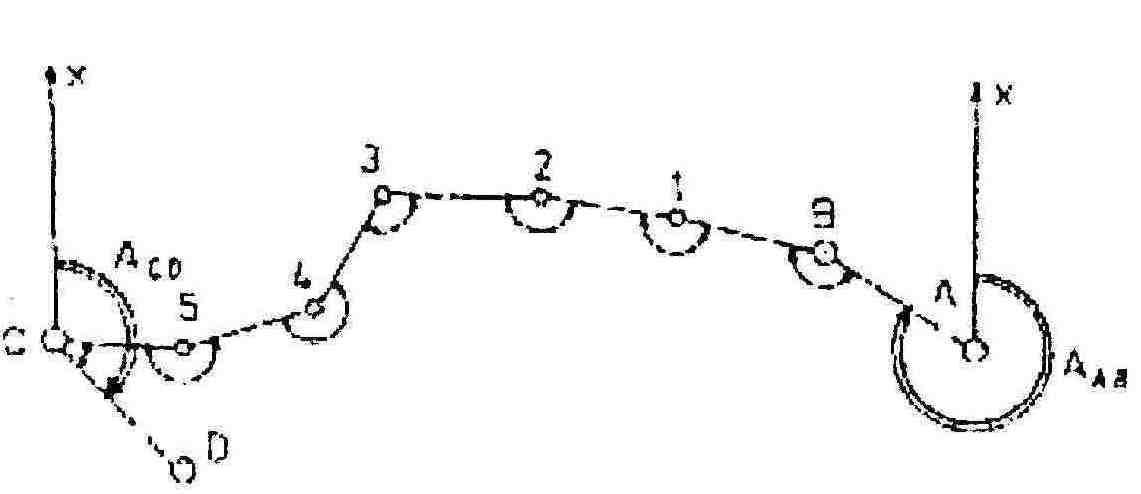
Ciąg otwarty najczęściej wychodzi z dwóch punktów o znanych współrzędnych i kończy się również na dwóch punktach o znanych współrzędnych. Obliczenie otwartego ciągu sytuacyjnego dwustronnie nawiązanego wykonuje się w sposób podobny jak ciągu zamkniętego.

Istnieją dwie różnice w trybie prowadzonych obliczeń; pierwsza dotyczy obliczenia teoretycznej sumy kątów w ciągu, a druga - obliczenia teoretycznej sumy przyrostów. Teoretyczna suma kątów lewych w ciągu dwustronnie nawiązanym wynosi:

Σα = A_K + n·200^g-A_P

Dla kątów prawych teoretyczna suma kątów przedstawia się następująco:

Σα_p = A_P + n·200^g-A_K

gdzie: Ap - azymut początkowy oparty na punktach nawiązania, obliczony ze współrzędnych, Ak — azymut końcowy, n - ilość pomierzonych kątów w ciągu.

Teoretyczna suma przyrostów dla dwustronnie nawiązanego ciągu otwartego

przedstawia się następująco:

ΣΔx_t = X_K - X_P

ΣΔy_t = Y_K - Y_P

gdzie: Xk, Yk - współrzędne punktu końcowego ciągu,

Xp, Yp - współrzędne punktu początkowego ciągu.

---