Egzamin z MB, 23.06.2006r. - I termin IIIr., sem.6; St. Dz. Mgr

1.

I) Znając ogólne rozwiązanie równania osi odkształconej pręta poddanego działaniu siły osiowej wyprowadzić wzory transformacyjne dla pręta utwierdzonego na jednym końcu i przegubowo podpartego na drugim dla przypadków:

a) ściskania,

b) rozciągania pręta.

II) Dla układu prętowego obciążonego w przegubie B siłą o składowej poziomej P₁ i pionowej P₂ o zwrotach zaznaczonych na rysunku wyprowadzić najprostszą postać równania, z którego można wyznaczyć wartości sił krytycznych P.

Dane: EJ. P₁=P, P₂=2P.

C

EJ 3,0m

P₂

P₁

B

3,0m

EJ

A

4,0m

2.

Dla ramy o masie m skupionej w węźle C i prętach o sztywnościach na zginanie EJ:

a) określić liczbę dynamicznych stopni swobody układu,

b) stosownie do przyjętych współrzędnych uogólnionych q opisujących ruch układu wyznaczyć macierz podatności [D] oraz macierz sztywności [K].

Wykazać, że [D]^-1=[K] lub [K]^-1=[D],

c) zapisać równanie ruchu w dwóch wersjach:

- korzystając z macierzy podatności [D],

- korzystając z macierzy sztywności [K].

Dla obu przypadków wyprowadzić równanie, z którego można wyznaczyć wartości częstości kołowych drgań własnych układu.

3.

I) Wyprowadzić równanie poprzecznych drgań własnych pręta prostego o długości L, sztywności na zginanie EJ i gęstości liniowej μ (w postaci ogólnej).

II) Dla belki o schemacie statycznym podanym na rysunku wyprowadzić wzory transformacyjne przy założeniu, że amplituda kąta obrotu (wymuszenie kinematyczne) podpory k wynosi ϕ_k.

4.

Dla belki ściskanej siłą osiową N można określić wartość najmniejszej siły krytycznej korzystając ze wzoru:

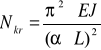
gdzie współczynnik a zależy od warunków brzegowych ściskanej belki. Wyznaczyć go dla belki o schemacie statycznym podanym na rysunku.

Wskazówka: Wykorzystać rozwiązanie równania różniczkowego osi odkształconej belki ściskanej siłą osiowa.

---