Akademia Techniczno-Humanistyczna

w Bielsku-Białej

Wydział Budowy Maszyn i Informatyki

Semestr II

ĆWICZENIE NR 40

Wyznaczanie współczynnika lepkości cieczy metodą Stokesa.

Maria Schodnicka

1. Cel ćwiczenia

Celem ćwiczenia jest wyznaczenie współczynnika lepkości gliceryny dla różnych temperatur z wykorzystaniem metody Stokesa.

2. Wstęp teoretyczny

We wszystkich cieczach przy ruchu jednych warstw cieczy względem drugich występuje zjawisko tarcia wewnętrznego a siła tego oddziaływania wyraża się wzorem :

gdzie : Δv - jest różnicą prędkości dwóch warstw cieczy odległych od siebie o odcinek Δz

η - jest współczynnikiem tarcia wewnętrznego (lepkości). Współczynnik ten zależny jest od rodzaju cieczy i dla cieczy jest odwrotnie proporcjonalny do temperatury. Jednostką współczynnika lepkości jest N⋅s/m² lub pauz (1 pauz= 0,1 N⋅s/m²).

Dla niewielkich prędkości ciała w cieczy występuje ruch warstwowy (laminarnym). W tym przypadku warstwa cieczy przylegająca bezpośrednio do ciała porusza się wraz z nim , a kolejne warstwy cieczy unoszone są coraz wolniej , natomiast gdy prędkości ciała są duże, w cieczy występuje ruch wirowy (turbulentny).

Dla kuli poruszającej się w cieczy Stokes wyprowadził następujący wzór :

F = 6η π r v

w którym: η - współczynnik lepkości

r - promień kuli

v - prędkość kuli

przy czym wzór ten jest słuszny dla warstwowego opływania kuli przez ciecz .

Dla kuli spadającej swobodnie w cieczy

Powyższy wzór jest słuszny tylko wówczas , gdy ruch kulki nie wywołuje ruchu burzliwego cieczy. Warunkom tym odpowiadała kula o średnicy rzędu kilku milimetrów , spadająca w naczyniu z gliceryną. Na kulkę spadającą swobodnie działa ku górze siła tarcia wewnętrznego F , wynikająca z prawa Stokesa oraz siła wyporu F₁.Ku dołowi działa siła ciężkości Q , określona prawem Newtona. Siły te można wyrazić odpowiednio:

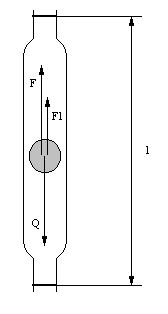
Symbole : r,ρ,m i v oznaczają odpowiednio - promień, gęstość , masę i prędkość spadania kulki, symbole D,ρ₁ i η - ciężar właściwy, gęstość oraz współczynnik lepkości cieczy. V jest objętością wypartej cieczy przez zanurzoną w niej kulkę , równą objętości tej kulki a g - przyśpieszeniem ziemskim.

Początkowo kulka będzie się poruszać ruchem przyśpieszonym. Z chwilą zrównoważenia sił F,F₁ i Q ruch kulki będzie jednostajny. Mierząc drogę l przebytą przez kulkę ruchem jednostajnym oraz czas jej przebycia t a także korzystając z warunku równowagi sił, można wyznaczyć lepkość dynamiczną cieczy w postaci zależności :

Przyrządy użyte w ćwiczeniu :

-rura Stokesa wypełnia gliceryną

-waga analityczna

-śruba mikrometryczna

-kulki

-urządzenie do podgrzewania ,termometr

-stoper

Przebieg ćwiczenia :

1. Wyznaczyliśmy masę dziesięciu kulek za pomocą wagi technicznej następnie za pomocą wagi analitycznej

waga analityczna (pomiar pierwszy): m=630,8 [mg]

waga analityczna (pomiar drugi): m=630,1 [mg]

2. Wyznaczyliśmy masę m pojedynczej kulki oraz błąd popełniony przy wyznaczaniu masy pojedynczej kulki Δm i Δm_śr.

Masa pojedynczej kulki:

m=63,1 [mg]

m=63,0 [mg]

Δm=0,1 [mg]

Masa średnia kulek:

m = 630,5 [mg]

m_śr = 1/10⋅ 630,5 = 63,1 [mg] = 0,0000631 [kg]

m = 630,1 [mg]

m_śr = 1/10⋅ 630,1 = 63,0 [mg] = 0,0000630 [kg]

Δm_śr = m_śr1-m_śr2 (dla dziesięciu kulek)

Δm_śr = 0,1 [mg] = 0,0000001 [kg]

3. Zmierzyliśmy średnicę d każdej kulki i oszacowaliśmy błąd bezwzględny Δd popełniony przy pojedynczym pomiarze:

Błąd bezwzględny pomiaru Δd:

gdzie k - liczba działek, 1/n - skok gwintu śruby

4. Zmierzyliśmy długość drogi l opadania kulek oraz oszacowaliśmy błąd bezwzględny pomiaru Δl wyniki zanotowaliśmy w tabeli I.

m [mg]	Δm [mg]	mśr [mg]	Δmśr [mg]	d [mm]	Δd [mm]	l [m]	Δl [m]	ρ[kg/m^3]
63,1	0,1	63,1	0,1	2,48	0,01	0,5	0,002	1260
63,0				63,0		2,47	0,01			1263
				2,47	0,01					1267
										2,48	0,01			1270
										2,47	0,01			1273
										2,47	0,01			1277
										2,48	0,01			1280
										2,46	0,01
										2,46	0,01
										2,47	0,01

5. Pomiary czasu opadania kulek przeprowadziliśmy w czterech temperaturach począwszy od temperatury otoczenia wynoszącej 20,2^oC poprzez 25,2^oC, 30,2^oC, 35,3^oC, 40,2^oC, 45,2^oC aż do 50,1^oC.

6. Wyznaczyliśmy czas t opadania każdej kulki , następnie obliczyliśmy wartość średnią

ze wzoru:

dla temperatury 20,2^oC

dla temperatury 25,2^oC

dla temperatury 30,2^oC

dla temperatury 35,3^oC

dla temperatury 40,2^oC

dla temperatury 45,2^oC

dla temperatury 50,1 ^oC

T[^oC]	t1[s]	t2[s]	t3[s]	t4[s]	t5[s]	tśr[s]	Δtśr[s]
20,2	5,03	4,94	5,10	5,04	4,97	5,02	0,0034
25,2	3,66	3,62	3,59	3,66	3,70	3,65	0,0034
30,2	2,78	2,97	3,00	2,94	2,91	2,92	0,0033
35,3	2,46	2,56	2,41	2,41	2,56	2,48	0,0032
40,2	2,19	2,09	2,09	2,00	2,03	2,08	0,0032
45,2	1,94	1,88	1,81	1,84	1,94	1,88	0,0031
50,1	1,69	1,65	1,66	1,69	1,62	1,66	0,0031

7. Gęstość gliceryny jest zależna od temperatury. W temperaturze 20°C gęstość gliceryny ρ₁ = 1260 [kg/m³]. Aby obliczyć gęstość gliceryny ρ_o w innej temperaturze, stosujemy wzór:

ρ_{o =} ρ (1 + γ⋅Δt)

gdzie γ to współczynnik rozszerzalności objętościowej cieczy, a Δt to przyrost temperatury wyrażony w K.

Dla gliceryny γ wynosi 0,00053 [K^-1].

ρ₁ = 1260 [kg/m³]

Temperatura 20,2°:

Δt =0,2 [K]

ρ ₌ ρ₁ (1 + 0,00053⋅0,2)=1260(1+0,000106)=1260 [kg/m³]

Temperatura 25,2°:

Δt =5,2 [K]

ρ ₌ ρ₁ (1 + 0,00053⋅5,2)=1260(1+0,002715)=1263 [kg/m³]

Temperatura 30,2°:

Δt =10,2 [K]

ρ ₌ ρ₁ (1 + 0,00053⋅10,2)=1260(1+0,005406)=1267 [kg/m³]

Temperatura 35,3°:

Δt =15,3 [K]

ρ ₌ ρ₁ (1 + 0,00053⋅15,3)=1260(1+0,008109)=1270 [kg/m³]

Temperatura 40,2°:

Δt =20,2 [K]

ρ = ρ₁ (1+0,00053⋅20,2) = 1260 (1+0,010706) = 1273[kg/m³ ]

Temperatura 45,2°:

Δt =25,2 [K]

ρ = ρ₁ (1+0,00053⋅25,2) = 1260 (1+0,013356) = 1277 [kg/m³ ]

Temperatura 50,1°:

Δt =30,1 [K]

ρ = ρ₁ (1+0,00053⋅30,1) = 1274 (1+0,015953) = 1280 [kg/m³ ]

8. Obliczyliśmy lepkość dynamiczną cieczy dla każdej z rozpatrywanych temperatur:

9. Sporządziliśmy wykres η(T) wyznaczając przedział błędu , który wyznaczamy ze wzoru :

Błąd Δt_α wartości średniej t wyznaczyliśmy stosując rozkład Studenta-Fischera przyjmując poziom ufności α=0,96 :

gdzie t_n,α - współczynnik dla ilości pomiarów n i poziomu ufności α

S_x - odchylenie standartowe średniej.

Więc:

Δt_α= 2,262 ⋅ 0,051 = 0,12 [s]

Więc:

Δt_α= 2,262 ⋅ 0,038 = 0,09 [s]

Więc:

Δt_α= 2,262 ⋅ 0,076 = 0,17 [s]

Więc:

Δt_α= 2,262 ⋅ 0,065= 0,15 [s]

Więc:

Δt_α= 2,262 ⋅ 0,052= 0,12 [s]

Więc:

Δt_α= 2,262 ⋅ 0,020= 0,04 [s]

Błąd lepkości:

Temperatura 20,2°C:

Temperatura 25,2°C:

Temperatura 30,2°C:

Temperatura 35,3°C:

Temperatura 40,2°C:

Temperatura 45,2°C:

Temperatura 50,1°C:

Tabela wyników :

T[°C]	η [N⋅s/m^2] Δη
20,2	2,63 0,09
25,2	1,91 0,06
30,2	1,53 0,11
35,3	1,30 0,93
40,2	1,09 0,09
45,2	0,99 0,07
50,1	0,87 0,03

Wnioski i dyskusja rezultatów:

Błędy otrzymanych wartości wiążą się z :

• Ograniczeniami w dokładności pomiarów wynikającymi z niedoskonałości przyrządów pomiarowych

• Niedokładnością pomiarów czasu wynikłą z ręcznego włączania i wyłączania stopera

• Zaburzeniami prędkości kuleczek wynikłymi z tego, że zostały one wrzucone zbyt blisko ścianki rury Stokesa

- Przyczyną powstania największego błędu jest niedokładność pomiaru czasu opadania kulki. Wynika to z małej czułości mierzącego.

- Do pomiaru należy używać kulek o małej gęstości, gdyż to pozwala na zwiększenie czasu spadania kulki (zmniejszenie prędkości opadania), co znacznie zwiększa dokładność pomiaru.

- Współczynnik lepkości jest odwrotnie proporcjonalnie do temperatury

Rozważany ruch cieczy jest ruchem warstwowym (laminarnym), który występuje przy małych prędkościach. Dla dużych prędkości ruch cieczy staje się bezładnym - wirowym (turbulentnym). Do opisu lepkich własności cieczy stosuje się drugi parametr ν nazywany kinematycznym współczynnikiem lepkości. Dla ustalenia warunków kiedy ruch cieczy przechodzi z laminarnego w burzliwy służy liczba Reynoldsa.

1

Strona 2

---