AKADEMIA BYDGOSKA

Im. Kazimierza Wielkiego

W BYDGOSZCZY

Instytut techniki

Sprawozdanie z ćwiczenia

Wyznaczanie momentu tarcia w łożyskach i momentu hamowania

Wykonanie: Mariusz Rut

Łukasz Dzięcioł

II WT/C

Bydgoszcz 2003

1. Cel ćwiczenia

Celem ćwiczenia jest wyznaczenie momentu tarcia w łożyskach tocznych oraz momentu hamowania układu mas wirujących.

2. Wstęp

We wszystkich łożyskach ślizgowych i tocznych występuje tarcie. Jest ono niekorzystne, ponieważ wywołuje rozpraszanie energii i wydzielanie się ciepła. W celu ilościowego ujęcia oporów tarcia w łożyskach operuje się tzw. momentem tarcia M_t, który jest równy iloczynowi pewnej umownej siły tarcia T_ł w łożysku i jej ramienia r:

Wartość siły tarcia zależy od siły nacisku R będącej reakcją podporową w miejscu łożyskowania:

gdzie μ_ł jest współczynnikiem tarcia łożyska.

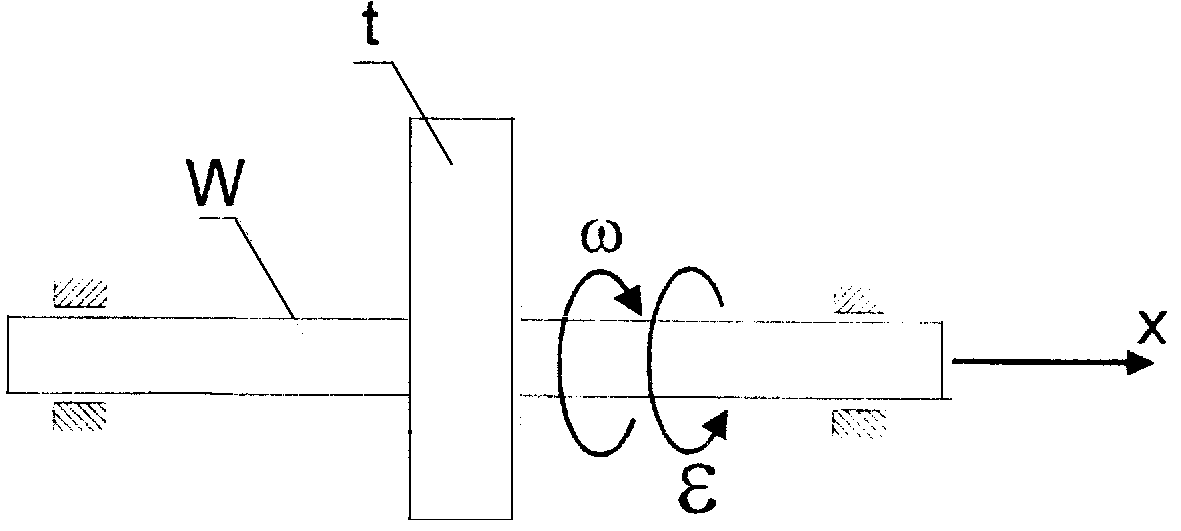
Na poniższym rysunku znajduje się wałek wraz z tarczą, obracający się wokół osi x.

Wałek podparty jest na dwóch łożyskach, w których występuje tarcie. Jeżeli przyłożymy do układu pewien moment napędowy a następnie odejmiemy go, to układ będzie się nadal obracał w wyniku działania jego bezwładności. Ruch ten będzie hamowany przez momenty tarcia w łożyskach, a równanie tego ruchu ma postać:

gdzie:

M_t - łączny moment tarcia [Nm]

J - masowy moment bezwładności układu wirującego [kgm²]

ε_s - opóźnienie kątowe ruchu [rad/s²]

Przyjmuje się, że ruch ten jest ruchem obrotowym jednostajnie opóźnionym ze stałym opóźnieniem ε_s. Opóźnienie to może więc być wyrażone wzorem:

gdzie ω jest prędkością kątową ruchu w rad/s, a t czasem w sekundach. Prędkość kątową oblicza się na podstawie prędkości obrotowej n:

Podstawiając wzór na prędkość kątową do wzoru na opóźnienie otrzymujemy:

Spadek obrotów Δn można odnieść do dowolnego przyrostu czasu Δt. Jeżeli rozpatrzymy cały czas ruchu obrotowego, wówczas: Δn=n₀, Δt=t_s, gdzie:

n₀ - prędkość obrotowa układu na początku ruchu (dla t=0)

t_s - całkowity czas ruchu.

Ostatecznie wzór na opóźnienie kątowe ma postać:

Natomiast wzór na moment tarcia w łożyskach dla układu z jedną tarczą ma postać:

gdzie J jest momentem bezwładności układu z jedną tarczą [kgm²].

W układzie z jedną tarczą, który jest hamowany za pomocą hamulca wywierającego stały moment hamowania M_h również występuje ruch obrotowy jednostajnie opóźniony:

Opóźnienie ε_h kątowe tego ruchu jest wyrażone wzorem:

gdzie:

n₀ - predkość obrotowa na początku ruchu, w chwili przyłożenia hamulca w obr/min

t_h - całkowity czas ruchu w sekundach.

Moment hamowania jest równy: M_h=Jε_h-M_ł [Nm].

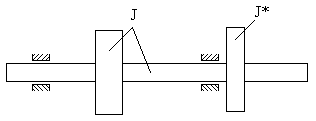
Do powyższego układu można dołożyć dodatkową tarczę o momencie bezwładności J*, co jest przedstawione na poniższym rysunku:

W przypadku ruchu swobodnego, hamowanego tylko tarciem w łożyskach, opóźnienie kątowe ε_s* wynosi:

gdzie t_s* to czas ruchu układu do zatrzymania. Moment tarcia w łożyskach jest równy:

Dla układu z dwoma tarczami poddanego hamowaniu opóźnienie ε_h* wyraża wzór:

a moment hamowania Mh* jest równy:

3. Obliczenia

Obliczenie momentu bezwładności J układu obrotowego z jedną tarczą

Wzór na moment bezwładności walca:

Aby wyliczyć J walca należy znać jego masę, którą obliczymy ze wzoru:

Gdzie R jest promieniem walca, h - wysokością, ρ - gęstością materiału, z którego jest wykonany walec. Badany układ można podzielić na pojedyncze walce, a następnie obliczyć ich momenty bezwładności i zesumować je ze sobą otrzymując moment bezwładności całego wałka.

Badany wałek był wykonany ze stali węglowej, której ciężar właściwy wynosi 7,7 kG/dm3.

Gęstość stali węglowej ρ wynosi:

Masy poszczególnych części wałka wynoszą:

(πρ)(R²_nh_n)

1. (3,14•0,78)98 = 2,45•98 = 240,1 = 0,0024kg

2. (3,14•0,78)4000 = 2,45•4000 = 9800 = 0,098kg

3. (3,14•0,78)10937,5 = 2,45•10937,5 = 26796,8 = 0,27kg

4. (3,14•0,78)7056 = 2,45•7056 = 17287,2 = 0,17kg

5. (3,14•0,78)165000 = 2,45•165000 = 404250 = 4,04kg

6. (3,14•0,78) 64176 = 2,45•64176 = 157231,2 = 1,57kg

7. (3,14•0,78) 165000 = 2,45•165000 = 404250 = 4,04kg

8. (3,14•0,78) 7056 = 2,45•7056 = 17287,2 = 0,17kg

9. (3,14•0,78) 10937,5 = 2,45•10937,5 = 26796,8 = 0,27kg

10. (3,14•0,78) 4000 = 2,45•4000 = 9800 = 0,098kg

11. (3,14•0,78) 243 = 2,45•243 = 595,35 = 0,006kg

12. (3,14•0,78)1728 = 2,45•1728 = 4233,6 = 0,042kg

Razem daje to ok. 10,78kg masy wałka z tarczą.

Obliczamy momenty bezwładności poszczególnych części wałka:

J₁=0,0024•7²/2=0,06

J₂=0,098•10²/2=4,9

J₃=0,27•12,5²/2=21,09

J₄=0,17•28²/2=66,64

J₅=4,04•100²/2=20200

J₆=1,57•95,75²/2=7196,93

J₇=4,04•100²/2=20200

J₈=0,17•28²/2=66,64

J₉=0,27•12,5²/2=21,09

J₁₀=0,098•10²/2=4,9

J₁₁=0,006•9²/2=0,24

J₁₂=0,042•8²/2=1,34

J₁+J₂+...+J₁₁+J₁₂=47783,83

Moment bezwładności całego wałka wraz z tarczą wynosi: J=47783,83

Obliczenie momentu bezwładności J* dodatkowej tarczy oraz nakrętki mocującej

Wymiary drugiej tarczy:

∅ = 199,94mm

∅ otworu = 18mm

grubość = 19,34mm

Wymiary nakrętki mocującej:

Obliczanie momentu bezwładności tarczy:

m = (πρ)(R²_nh_n) = 2,45•99²•19 = 456087,6 = 4,56kg

J* =

Obliczanie momentu bezwładności nakrętki:

m₁ = (πρ)(R²₁h₁) =

J₁*

m₂ = (πρ)(R²₂h₂) =

J₂* =

J*=J₁^*+J₂^* nakrętki wynosi 27,442kg/m²

Razem moment bezwładności dodatkowej tarczy i nakrętki wynosi: J* = 22372,242

3.1. Dla układu z jedną tarczą

Sposób hamowania	Numer pomiaru	Czas t[s]						Czas ruchu ts[s]	Opóźnienie kątowe [rad/s^2]	Opóźnienie średnie [rad/s^2]	Moment tarcia w łożyskach
				0	5	10	15					20	25
				Prędkość obr n[obr/min]
	Tarcie w łożyskach	1	30	20	10	5	1	0				0,1256	0,1256	5624,849
		2	30	22	14	12	2	0				0,1256
		3	30	22	14	7	2	0				0,1256
	Hamulec z masą m1=117,5g	1	30	0					4			0,785	0,785	31885,5
		2	30	0					4			0,785
		3	30	0					4			0,785
	Hamulec z masą m2=409,5g	1	30	0					2			1,57	1,57	69395,8
		2	30	0					2			1,57
		3	30	0					2			1,57

3.2.Dla układu z dwiema tarczami

Sposób hamowania	Numer pomiaru	Czas t[s]										Czas ruchu ts[s]	Opóźnienie kątowe [rad/s^2]	Opóźnienie średnie [rad/s^2]	Moment tarcia w łożyskach
				0	5	10	15	20	25	30	35					40
				Prędkość obr n[obr/min]
	Tarcie w łożyskach	1	30	25	17	14	10	6	3	0						0,089	0,085	6184
		2	30	25	20	15	10	6	3	1	0					0,078
		3	30	25	19	14	10	5	3	0						0,078
	Hamulec z masą m1=117,5g	1	30	0									3,5			0,89	0,89	605667,7
		2	30	0									3,5			0,89
		3	30	0									3,5			0,89
	Hamulec z masą m2=409,5g	1	30	0									2,5			1,25	1,25	847341,5

4.Wnioski

Moment tarcia zwiększa się po dołożeniu dodatkowej tarczy, a więc jest związany z masą. Wraz ze zwiększeniem się masy zwiększa się moment tarcia. Układ z dodatkową tarczą ma dłuższy całkowity czas obrotu.

∅20

∅25

∅25

∅20

∅14

∅56

∅200

∅56

∅18

∅16

40

70

40

70

40

2

3

9

9

27

7

6

13,6

45

28

∅14,2

---