Nr. ćw. 308	Data 27.05.01	Jakacki Zbigniew	Wydział Elektryczny	Semestr II	Grupa E-3
Prowadzący: mgr B. Jazurek			Przygotowanie	Wykonanie	Ocena

Temat: Wyznaczanie współczynnika załamania światła dla cieczy za pomocą refraktometru Abbego

1. Część teoretyczna.

Gdy promień świetlny biegnie z ośrodka optycznie rzadszego do optycznie gęstszego, np. z powietrza do szkła, ulega on załamaniu na granicy ośrodków, tworząc w ośrodku gęstszym mniejszy kąt z normalną do powierzchni (kąt załama­nia) niż w ośrodku rzadszym (odpowiedni kąt nosi nazwę kąta padania). W przy­padku odwrotnego biegu promieni kąt padania jest mniejszy od kąta załamania.

Każdemu kątowi padania a odpowiada inny kąt załamania β, lecz stosunek si­nusów obu kątów jest wielkością stalą dla danej pary ośrodków i dla danej długo­ści fali światła

Powyższy wzór wyraża prawo załamania światła (prawo Snella), a wielkości n₁ i n₂ nazywają się bezwzględnymi współczynnikami załamania światła ośrodka l i ośrodka 2.

Bezwzględny współczynnik załamania światła określony jest również stosun­kiem prędkości światła w próżni c do prędkości światła w danym ośrodku v

Ze względu na to, że prędkość światła jest największa w próżni, bezwzględny współczynnik załamania światła jest dla wszystkich ośrodków materialnych więk­szy od jedności.

Załamanie światła na granicy dwóch ośrodków materialnych określone jest ich względnym współczynnikiem załamania. Wielkość tą wyznaczamy z poniższego wzoru:

W rzeczywistych warunkach załamanie światła następuje często na granicy powietrza z cieczą lub ciałem stałym. W tej sytuacji można przyjąć, że powietrze posiada współczynnik załamania bardzo bliski wartości dla próżni (n = l) i że równanie

wyznacza bezwzględny współczynnik załamania cieczy lub gazu.

Wzór Snella przyjmuje szczególnie wygodną postać w przypadku cał­kowitego odbicia wewnętrznego zachodzącego przy kącie granicz­nym. Istotę zjawiska całkowitego odbicia wewnętrznego ilustruje poniższy rysunek. Promienie biegnące z ośrodka optycznie gęstszego (II) do rzadszego odchylają się od prostopadłej tym bardziej, im większy jest kąt padania α.

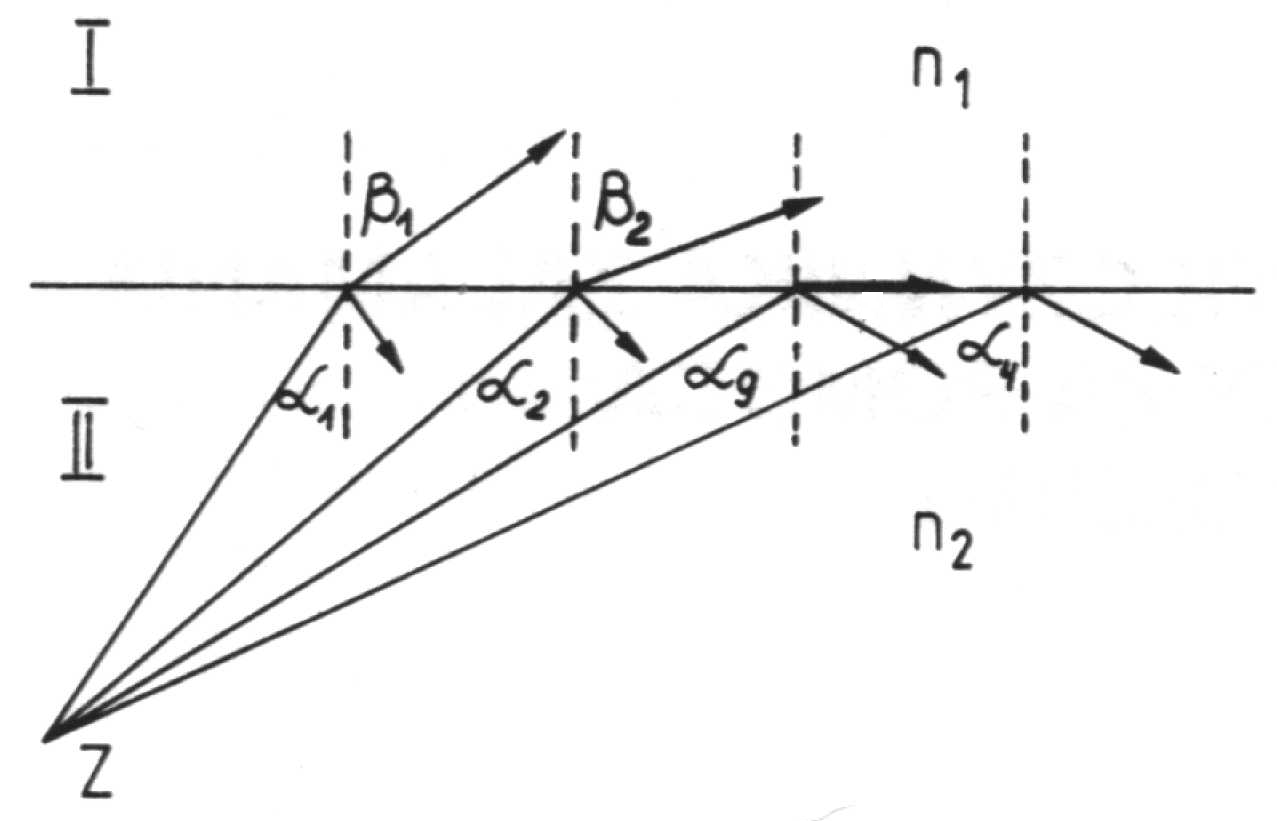
Ilustracja zjawiska całkowitego odbicia wewnętrznego.

Kąt załamania osiąga wartość 90° przy pewnym kącie α_g, zwanym kątem granicznym - promień nie przechodzi do ośrodka I. Widzimy więc, że przy kącie granicznym i większych kątach pada­nia promienie nie mogą przejść do ośrodka rzadszego - ulegają całkowitemu od­biciu. Zgodnie z prawem załamania

Znając współczynnik załamania n₁ ośrodka rzadszego oraz mierżąc kąt graniczny α_g, możemy wyznaczyć współczynnik załamania n₂ ośrodka gęstszego. Pomiaru kąta granicznego dokonujemy za pomocą refraktometru.

2. Przebieg ćwiczenia.

Przed przystąpieniem do ćwiczenia należy włączyć lampkę stołową i ustawić tak zwierciadła aby w lunetce była podświetlona zarówno skala jak i ekran. Następnie należy odchylić pryzmat, sprawdzić, czy jego powierzchnia jest sucha i czysta, po czym nałożyć na nią kilka kropel badanego roztworu i docisnąć pryzmat. Pokrętłem pryzmatów ustawić tak aby cały ekran był jednakowego koloru i odczytać na podziałce umieszczonej na dole współczynnik załamanie. Powtórzyć tą czynność dla roztworów o różnym stężeniu. Dla jednego z roztworów przeprowadzić pomiary w funkcji temperatury.

3. Pomiary i obliczenia.

Pomiary współczynnika załamania przy różnych stężeniach procentowych roztworu wodnego gliceryny wykonywałem przy temperaturze 28^oC.

δn = 0,001

Stężenie procentowe roztworu wodnego gliceryny	10 %	30 %	50 %	70 %
Współczynnik załamania n	1,58	1,59	1,632	1,645

Powyższy wykres przedstawia zależność α = f(c)

Pomiary współczynnika załamania przy wzrastającej temperaturze. Badany roztwór jest 70 %.

δT = 1^oC

δn = 0,001

Temperatura [^oC]	30	35	40	45	50	55	60	65
Współczynnik załamania n	1,515	1,52	1,505	1,485	1,468	1,442	1,414	1,408

Wykres obrazujący zależność α = f(t).

4. Wnioski.

Analizując powyższe wykresy mogę stwierdzić że współczynnik załamania zachowuje się liniowo tzn. wzrasta proporcjonalnie do wzrostu stężenia procentowego roztworu wodnego gliceryny.

Wykres współczynnika załamania w funkcji temperatury również jest linią prostą w początkowej fazie jest wyższy a następnie maleje.

Błędy pomiarowe powstałe podczas przeprowadzenia ćwiczenia uzasadniam zmęczeniem wzroku na skutek długotrwałego odczytu lub błędem paralaksy.

Wszystkie obliczenia zostały wykonane za pomocą programu Microsoft Excel.

---