Podstawy i algorytmy przetwarzania sygnałów(2)
Kierunek	Specjalność	Rok studiów	Symbol grupy lab.
Elektronika i Telekomunikacja		2	Wtorek/N, 13:15
Temat			Numer lab.
Porównanie filtrów typu FIR i IIR.			Ćwiczenie nr 10
Skład grupy ćwiczeniowej
Arkadiusz szczotka
Uwagi			Ocena

1. Projektowanie filtru o nieskończonej odpowiedzi impulsowej (IIR). Analiza wpływu rzędu filtru na charakterystyki amplitudowe i fazowe:

Filtry o nieskończonej odpowiedzi impulsowej do uzyskania próbki wyjściowej potrzebuje poprzednie próbki sygnału wejściowego oraz poprzednie próbki sygnału wyjściowego. Zmiany sygnału wejściowego filtru mogą spowodować powstanie na wyjściu niestabilności i oscylacji o nieskończonym czasie trwania na wyjściu filtru. Ta możliwość powstawania na wyjściu niezerowych próbek o nieskończonym czasie trwania, nawet jeśli sygnał wejściowy ma wartość zerową, jest nazywana nieskończoną odpowiedzią impulsową.

Zaprojektowałem filtr Butterworth'a o f_C = 0.1 Na wykresach wywoływanych za pomocą funkcji freqz zaobserwowałem jaki wpływ ma rząd zaprojektowanego filtru IIR na jego charakterystyki amplitudowe oraz fazowe.

Filtr Butterworth'a rzędu drugiego:

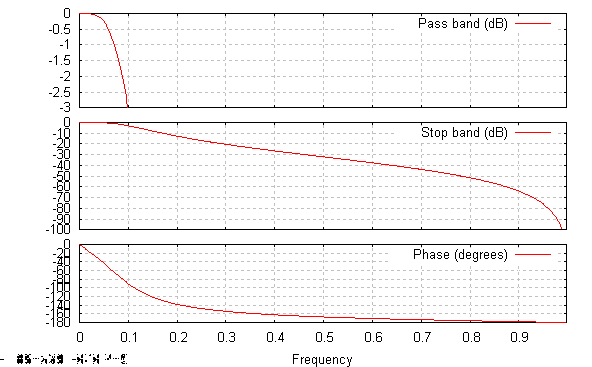
Filtr Butterworth'a rzędu piątego:

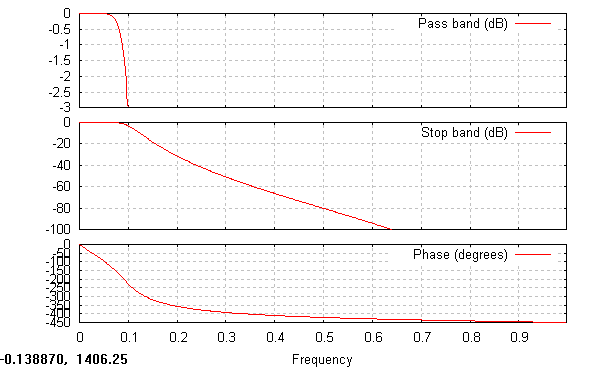
Filtr Butterworth'a rzędu dziesiątego:

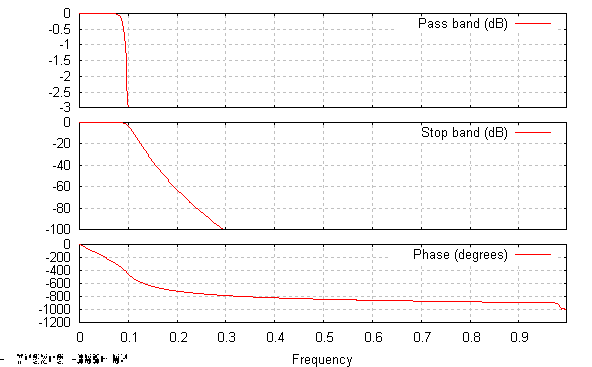
Na przedstawionych wykresach za pomocą funkcji freqz wyznaczyłem przebieg pasma przepuszczania, pasma zaporowego i fazy w dziedzinie częstotliwości w zależności od przyjętego rzędu filtru Butherworth'a. Zauważyłem, że im większy jest rząd filtru tym pasmo przepuszczania staje się bardziej wąskie i przyjmuje bardziej prostokątny kształt. Niezależnie od rzędu filtru faza w ma w przybliżeniu charakter liniowy, ale tylko w obszarze przepuszczania filtru. Im większy jest rząd filtru tym bardziej wzrasta tłumienie sygnału w dB poza pasmem przepuszczania.

2. Projektowanie filtru o skończonej odpowiedzi impulsowej (FIR). Analiza wpływu rzędu filtru na charakterystyki amplitudowe i fazowe:

Bieżącą próbkę sygnału w filtrach o skończonej odpowiedzi impulsowej wyjściowego uzyskuje się na podstawie próbki bieżącej i próbek przeszłych sygnału wejściowego. Dysponując skończonym ciągiem różnych od zera próbek sygnału wejściowego, filtr o skończonej odpowiedzi (FIR) zawsze ma na wyjściu skończonej ilości niezerowych próbek sygnału wyjściowego, stąd nazwa o skończonej odpowiedzi impulsowej.

Zaprojektowałem filtr FIR o f_C = 0.1, w argumentach funkcji fir1 nie stosowałem okna czasowego. Na wykresach wywoływanych za pomocą funkcji freqz obserwowałem jaki wpływ ma rząd zaprojektowanego filtru na jego charakterystyki amplitudowe oraz fazowe.

Filtr FIR rzędu piątego:

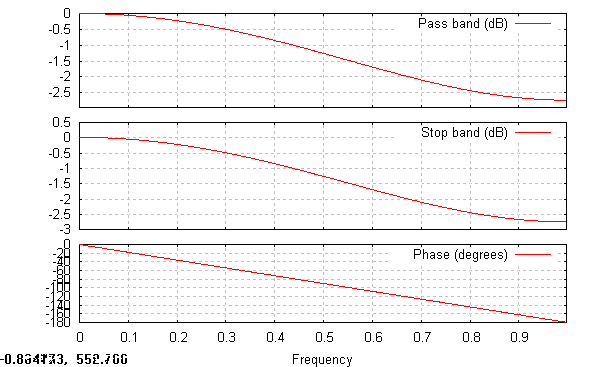
Filtr FIR rzędu dziesiątego:

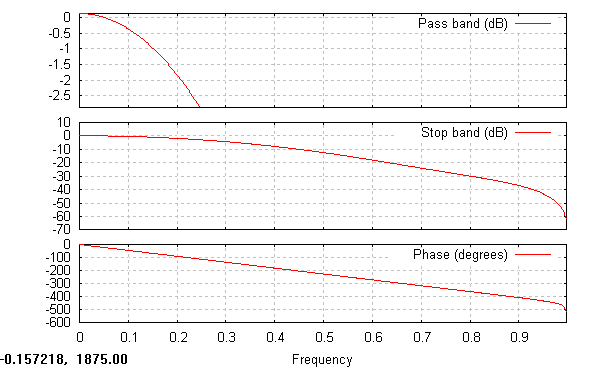
Filtr FIR rzędu dwudziestego:

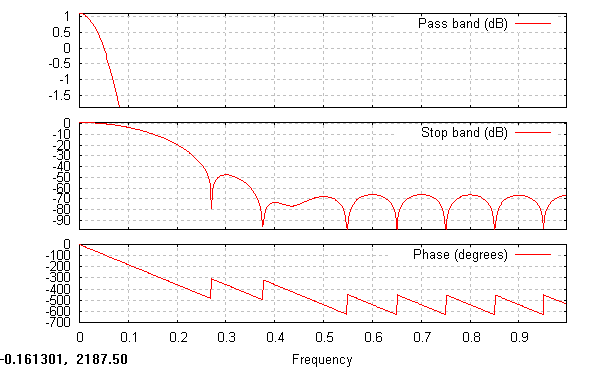
Z zamieszczonych wykresów widać, że szerokość pasma przepuszczania dla filtrów o skończonej odpowiedzi impulsowej bardzo silnie zależy od rzędu filtru. Im rząd filtru jest większy tym pasmo przepuszczania jest mniejsze. Konieczne jest przy tym stosowanie dużych rzędu filtrów, co wiąże się z dużą liczbą biegunów do obliczenia. Filtry FIR w przeciwieństwie do filtrów IIR mają zagwarantowaną liniowość fazy. W całym obszarze przepuszczania filtru faza jest liniowa, poza obszarem występują już zakłócenia liniowości, ale filtr tłumi w tym zakresie powyżej 50 dB i otrzymujemy bardzo mały sygnał. W paśmie zaporowym, tłumienie sygnału jest tym większe im większy jest rząd filtru i dzięki temu w poza obszarem przepuszczania dla filtru o wysokim rzędzie tłumienie ma bardzo dużą wartość i w praktyce całkowicie eliminuje sygnał.

3. Porównanie właściwości filtrów IIR w dziedzinie czasu i częstotliwości:

Analizie poddałem filtr Czebyszewa, Butterworth'a oraz filtr eliptyczny. Najpierw dokonam porównania filtrów IIR w dziedzinie czasu, zdefiniowałem sygnał x będący pobudzenie filtru, który w chwili początkowej ma wartość 1, a potem tylko 0.

Filtr Czebyszewa trzeciego rzędu o zafalowaniu w paśmie przepuszczającym 1 dB:

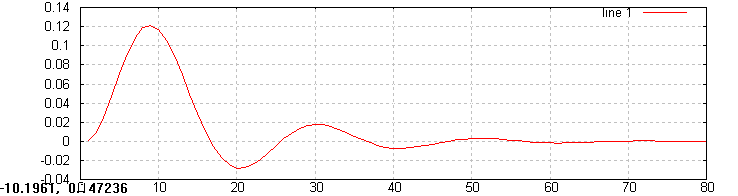
Filtr Butterworth'a trzeciego rzędu:

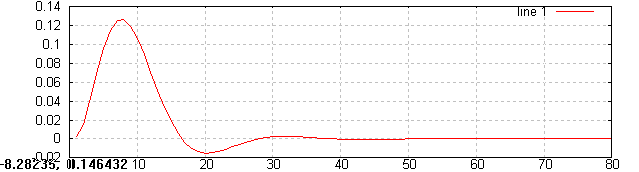
Filtr eliptyczny o zafalowaniu: w paśmie przepuszczania 0.5dB i zaporowym 40dB:

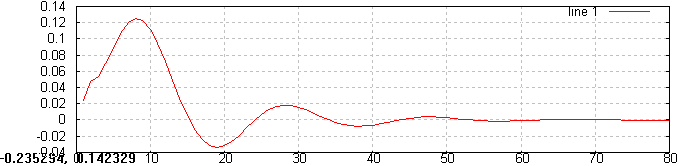
Z zamieszczonych wykresów zauważyłem, że dla sygnału wejściowego będącego jednostkowym pobudzeniem filtru mogą spowodowało powstanie na wyjściu oscylacji sygnału wyjściowego. Oscylacje te stopniowo zanikają i są potem ciężko zauważalne. Największe i najdłuższe wahania sygnału wyjściowego zaobserwowałem dla filtru Czebyszewa a na krótsze dla filtru Butherworth'a, wszystkie filtry były rzędu 3.

Następnie dokonałem analizy tych samych filtrów pobudzanych tym samym sygnałem jednostkowym w dziedzinie częstotliwości:

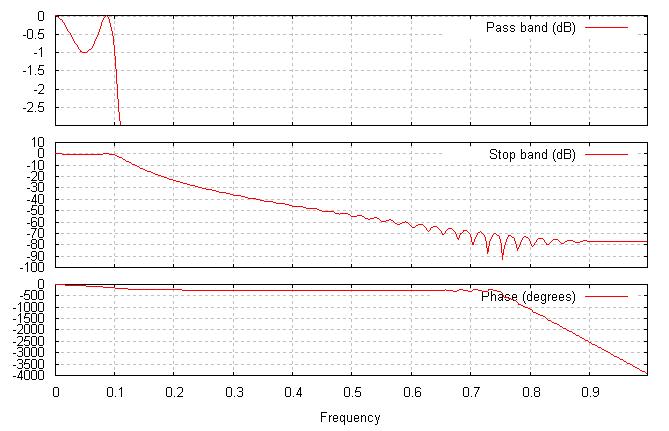
Filtr Czebyszewa trzeciego rzędu o zafalowaniu w paśmie przepuszczającym 1 dB:

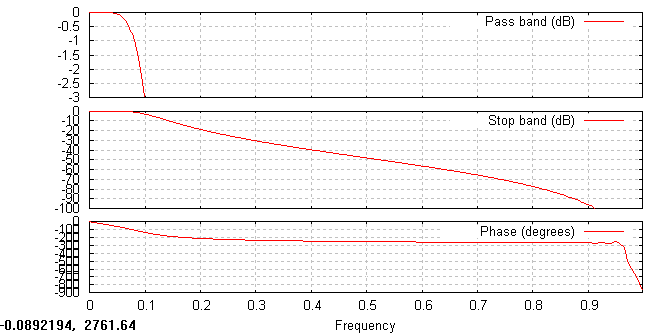
Filtr Butterworth'a trzeciego rzędu:

Filtr eliptyczny o zafalowaniu: w paśmie przepuszczania 0.5dB i zaporowym 30dB:

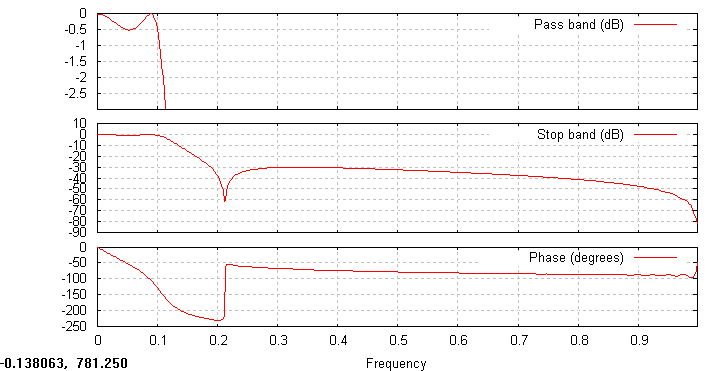
Każdy z powyższych filtrów ma inne cechy w dziedzinie częstotliwości. Filtr Czebyszewa w obszarze przepuszczania posiada największe zafalowanie amplitudy, a w obszarze zaporowym w pewnym zakresie częstotliwości sygnał posiadał stałą fazę. Filtr Butterworth'a posiada najbardziej płaską charakterystykę amplitudową w paśmie przepuszczania. Natomiast filtr eliptyczny poza pasmem przepuszczania zmienia fazę sygnału, a jego charakterystyka amplitudowa również wykazuje zafalowanie.

4. Zaprojektować filtr pasmowo-przepustowy w zakresie 300-3000Hz. Przefiltrować sygnał oraz projekt filtru powtórzyć dla kilku zadanych wartości tłumienia w paśmie zaporowym. Porównać wyniki (także odsłuchując zadane sygnały).

Wartość tłumienia 10dB:

Wartość tłumienia 30dB:

Wartość tłumienia 90dB:

Sygnały przefiltrowane filtrami o różnym współczynniku tłumienia w paśmie zaporowym różniły się od siebie, przede wszystkim dało się usłyszeć duże wytłumienie sygnału, tym większe im więcej było decybeli we współczynniku tłumienia. Powyżej 30dB wyraźnie słychać było mocne wytłumienie. Zgadzałoby się to z odczytami z powyższych wykresów. Widmo amplitudowe sygnału przefiltrowanego zmienia się dla kolejnych wartości tłumienia, staje się coraz rzadsze, a częstotliwości poza pasmem przenoszenia są mocno wytłumiane (90dB).

---