Laboratorium z wytrzymałości materiałów
Kierunek: MiBM	7. Statyczne pomiary tensometryczne. Pomiar naprężeń w zginanym dwuteowniku - teoria zginania.
Wydział: BMiZ
Rok: II
Semestr: IV
Grupa: M3
Weronika Moniuszko
Piotr Przybył
Michał Dymek
Mariusz Naraziński
Tomasz Izydorczyk
Data wykonania ćw.:	Data oddania sprawozdania:
12.04.2012r.	19.04.2012r.

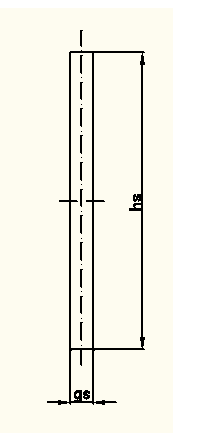
1. Szkic belki z usytuowanymi tensometrami.

L = 700 mm - długość pomiarowa

h_s = 82 mm - wysokość środnika

g_s = 5,2 mm - grubość środnika

2. Opis aparatury pomiarowej

Aparatura pomiarowa składała się z tensometrów rezystancyjnych foliowych umieszczonych na dwuteowniku, urządzenia powodującego zginanie dwuteownika oraz komputera, dzięki któremu mogliśmy obserwować wyniki pomiarów.

Zginanie mogliśmy regulować poprzez zmianę obciążenia, czy zmianę prędkości.

Na monitorze komputera (za pomocą specjalnego programu) mogliśmy odczytać wartości ugięcia u_D, naprężenia normalnego σ_A i stycznego τ_C.

3. Wyniki pomiarów.

Maksymalne ugięcie u_D , naprężenia normalne σ_A i styczne τ_C przy sile F = 15 kN

Lp.	x	Zmierzone			Teoretyczne
				uD	σA	τC	uD	σA	τC
	mm	Mm	MPa	MPa	mm	MPa	MPa
1	250	0,361	54,1	18,2	0,390	46,1	21,9
2	200	0,362	43,8	17,2	0,387	36,8	21,9
3	150	0,359	32,5	17,0	0,349	27,6	21,9
4	100	0,358	21,6	17,5	0,272	18,4	21,9
Średnia		0,360	- - -	17,5	0,346	- - -	21,9

4. Teoretyczne obliczenie u_D, σ_A, τ_C dla F = 15 kN i x = a.

• Równania statyki

gdzie:

F = 15 kN - siła gnąca

R_A, R_B - reakcje w podporach

• Analiza sił tnących T i momentów gnących M

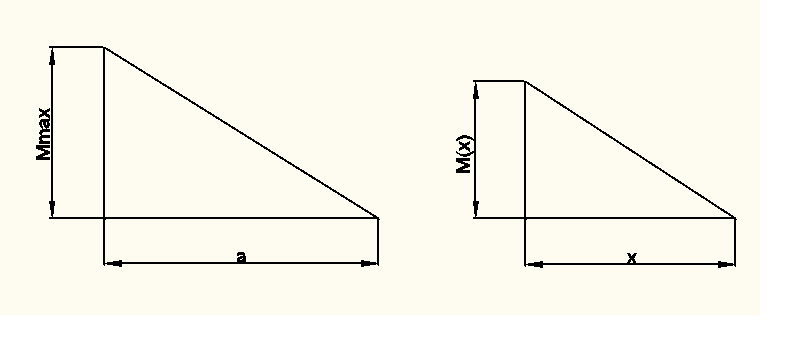
• Obliczanie naprężeń normalnych σ_A - (przekrój można uprościć ponieważ największe odkształcenie występują w osi środnika)

gdzie:

W_z - wskaźnik wytrzymałości na zginanie

M - moment gnący

σ - naprężenia normalne

, gdzie

I_z - moment bezwładności

ρ_max - maksymalna odległość włókien od środka ciężkości.

M(x) obliczymy z podobieństwa trójkątów

• Obliczanie naprężeń stycznych τ_C

gdzie:

S_z - moment statyczny

τ_max - naprężenia maksymalne

• Obliczanie ugięcia u_D metodą Clebscha

Belka podzielona na 14 części a = 50 mm

E = 205000 MPa

5. Wykresy

• Wykres zależności teoretycznej σ_A = σ(x)

• Wykres zależności teoretycznej τ_C = τ(x)

6. Wnioski

Ćwiczenie wykazało rozbieżność pomiędzy wynikami otrzymanymi z pomiaru odkształceń za pomocą tensometrów, a obliczeniami wykonanymi metodą analityczną. O możliwości wystąpienia tej różnicy należy pamiętać podczas projektowania, lepiej opierać się na wynikach badan doświadczalnych.

Naprężenia normalne maleją wraz ze zmniejszaniem odległości między podporą a punktem przyłożenia siły. Natomiast wartość naprężeń stycznych pozostaje bez zmian.

---