Wpływ temperatury, energii aktywacji, szybkości ścinania, naprężenia ścinającego, stężenia substancji na lepkośc
Temperatura: Dla większości cieczy lepkość maleje ze wzrostem temperatury
--> η = A * e Wa/ kT
gdzie:
A - współczynnik proporcjonalności
Wa - energia aktywacji lepkosci
k - stała Boltzmanna
T - temperatura bezwzgledna cieczy
Krew - lepkosć zwiększa się z obniżeniem temp (0o C - 2,5 razy wieksza niż przy 37o C) - zmiany podobne do wody - lekosć względna nie zależy od temperatury.
2. Energia aktywacji:
Założenie teorii lepkości cieczy - kazda czesteczka zajmuje położenie równowagi --> przejście jej w kierunku przepływu możliwe - gdy uzyska energię aktywacji lepkości (Wa)
Względna liczba cząsteczek majacych w danej temp energię aktywacji
--> Δna/n = e -Wa/kT
Wzrost temp cieczy --> wzrost predkości --> wzrost energii bezładnego ruchu cząsteczek --> wzrost wzglednej liczby czasteczek majacych energię większą od en aktywacji.
Po zlogarytmowaniu poprzedniego równania:
--> ln η = ln A +Wa/k * 1/T
wykres - linia prosta - wyznaczenie en aktywacji i współczynnika A.
Prędkość scinania - lepkość pozorna krwi - funkcja malejąca predkosci ścinania.
( przy 37o C i hematokrycie 45% i szybkości ścinania 0,1 s-1 --> 100mPas, przy 230 s-1 --> spadek do 4mPas).
Powody:
agregacja krwinek czerwonych przy małych prędkościach ścinania
deformacja i ukierunkowanie erytrocytów przy dużych predkościach ścinania
Wzrost pedkości ścinania - maleje agregacja --> maleje lepkosć krwi
Przy prędkościach > 150- 200 s-1 - deformacja erytrocytów - zmniejszenie lepkości krwi - z powodu zmniejszenia oddziaływan hydrodynamicznych.
Stężenie (nie wiem czy to jest dobrze, bo to wynika tylko z mojej interpretacji wzoru, nie znalazlem tego gdzie indziej, jak to znajdziecie, dajcie mi koniecznie znać! )
Lepkość rośnie ze wzrostem stężenia, bo:
η/ηo = 1 + 2,5 Φ (wzór Einsteina na lepkosć wzgledną r-ru)
Φ = c * NA * v / M
gdzie:
Φ - objętościowy współczynnik r-ru
c - stężenie r-ru
M - masa molowa
NA - l. Avogadra
v - objętość 1 cząstki
2.Właściwości reologiczne krwi
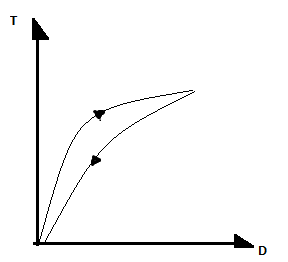
Krew jest cieczą nienewtonowską o charakterze pseudoplastycznym i tiksotropowym. Jej nienewtonowski charakter polega na tym, że stosunek naprężenia ścinającego do gradientu prędkości w danych warunkach ciśnienia i temperatury dla danej cieczy nie jest stały. Jeśli maleje on monotonicznie wraz ze wzrostem gradientu prędkości i nie zależy od czasu i sposobu ścinania, to mówimy o cieczy pseudoplastycznej. Jeśli stosunek ten zależy nie tylko od szybkości, ale też od czasu i sposobu ścinania, to ciecz nazywamy tiksotropową. Dla cieczy tiksotropowych krzywa płynięcia wykazuje histerezę.
Właściwości tiksotropowe krwi są związane z tworzeniem struktur w warunkach braku ścinania oraz ich rozpadaniem się w obecności naprężeń ścinających. Strukturami tymi są skupiska krwinek czerwonych; ich tworzenie się nazywamy agregacją.
Odtwarzanie struktur odbywa się w bardzo krótkim czasie, więc histereza krzywej płynięcia krwi jest prawie niezauważalna.
3.Krzywa płynięcia krwi
Przepływ cieczy lepkiej możemy traktować jako jeden ze specjalnych przypadków odkształcenia postaci materii. Oddziaływania występujące w przepływających płynach można scharakteryzować, podając naprężenia styczne (Τ=F/S) jako funkcję prędkości ścinania (u=dv/dx). Wykres zależności Τ=f(u) nazywamy krzywą płynięcia; na jej podstawie różnicujemy płyny na:
newtonowskie- wykresem jest linia prosta przechodząca przez początek układu współrzędnych
nienewtonowskie- wykresem jest linia prosta, która nie przechodzi przez początek układu współrzędnych.
Podział ten stosujemy dla ustalonych warunków ciśnienia i temperatury. Wartość ilorazu Τ/u nazywamy lepkością płynu. (η).
5. Krzywa pozornej lepkości krwi od prędkości ścinania, wartości przykładowe.
Lepkość pozorna krwi maleje wraz ze wzrostem prędkości ścinania. Przy temperaturze 37stopni C i hematokrycie 45% oraz prędkości ścinania 0,1 1/s wynosi 100mPas. Wzrost prędkości ścinania do 230 1/s powoduje spadek lepkości pozornej do około 4mPas.
Zależność ta wynika z dwóch zjawisk:
-agregacji erytrocytów(główny czynnik dla małych prędkości ścinania)
-deformacji i ukierunowaniu erytrocytów(główny czynnik dla dużych prędkości ścinania)
Wysoka prędkość ścinania prowadzi do zmniejszenia stopnia agregacji erytrocytów, a tym samym do spadku lepkości cieczy.
Przy prędkości ścinania około 150mPas-200mPas dochodzi do zjawiska deformacji erytrocytów i również spadku lepkosci w skutek zmniejszenia odzialywań hydrodynamicznych.
WYKRES- s.640 JAROSZYK 18.19
4.Prawo Ostwalda
Prawo dysocjacji Ostwalda nie pauje ni chuj do tematu! Skłaniam się ku temu, że chodzi tu o wyprowadzenie wzoru na lepkość względną w wiskozymetrze Ostwalda.
6. Równanie Cassona + Granica Płynięcia
Granica płynięcia - naprężenie powyżej którego krew dopiero zaczyna płynąć.
Krew - posiada granicę płynięcia - ale trudna do oznaczenia - przyczyny metodyczne.
Określenie granicy --> przy pomocy reologicznego modelu Cassona - wyraża w sposób analityczny krzywą płynięcia krwi
τ½ = τ0½ + kc * D½ <-- równanie Cassona
gdzie:
τ - naprężenie ścinające (styczne do powierzchni)
D - szybkość ścinania
τ0 - granica płynięcia
kc - współczynnik konsystencji
Według dotychczasowych badań - granica płyniecia krwi ~5mPa.
Wpływ na jej wartość maja:
hematokryt
-stężenie fibrynogenu i innych składników białkowych osocza
Wyznaczanie granicy płyniecia - ekstrapolacja krzywej płynięcia do prędkości równej 0.
Przykładowa krzywa płyniecia krwi w układzie pierwiastkowym dla krwi prawidłowej i krwi chorych na miażdżycę zarostową kończyn dolnych znajdziecie na stronie 600 Jaroszyka (rozdział 18.6.1 ryc 18.18)
8. Podatnosc erytrocytów na deformacje, rola w przepływie
Deformacje erytrocytów zachodzą przy prędkościach ścinania powyżej 150-200 1/s, które Są powodem zmniejszenia lepkości krwi (zmniejszenia oddziaływań hydrodynamicznych) i ich agregacji.
Przy prędkości ścinania 50/s krwinki mają kształt elipsoid, po zaniku ścinania powracają do pierwotnych kształtów. Agregacja może mieć znaczenia w miejscach o zwolnionym gradiencie prędkości (np. naczynia włosowate). (Pilawski str600)
10,Zależność lepkości od hematokrytu
Lepkość rośnie wraz ze wzrostem hematokrytu (przy 95% nadal jest zachowuje płynność)
Przy stałej prędkości ścinania porównuje się lepkośc skorygowaną (w odniesieniu do hematokrytu-45%).
η.krwi/η.osocza= exp{αH} gdzie α- współczynnik upakowania erytrocytów, H- hematokryt.
Lub η.krwiη.osocza45%=η.krwiη.osoczaH45H Lewa= lepkość wzgl. Przy H=45% ; Prawa= lepkość wzgl. Przy hematokrycie naturalnym podniesionym do potęgi (stosunku H standardowego do naturalnego)
7.
Elastyczność erytrocytów, która związana jest z ich zdolnością do odkształcania, powoduje większą lepkość krwi. Wysokie prędkości ścinania, które powodują zmniejszenie odkształcalności (ale zwiększenie odkształcenia…), są przyczyną spadku lepkości.
Zdolność erytrocytów do odkształcania wiąże się z:
Brakiem jądra
Małą lepkością cytoplazmy
Korzystnymi właściwościami lepko-sprężystymi błony
Dużą wartością stosunku powierzchni swobodnej do objętości
Zmniejszona odkształcalność krwi jest przyczyną wielu chorób.
9.
Największy wpływ na lepkość krwi przy stałym hematokrycie i małych prędkościach ścinania ma zjawisko agregacji krwinek czerwonych.
Im silniejsza agregacja tym większa lepkość krwi.
Im większa prędkość ścinania tym mniejsza agregacja
Przy prędkościach ścinania powyżej 150-200 s-1 występuje zjawisko deformacji krwinek czerwonych, co powoduje mniejszą lepkość wskutek zmniejszenia oddziaływań hydrodynamicznych.
11.Wiskozymetr Ubbelohde'a,
Pomiar lepkość względnej roztworów potrzebne do sporządzenia wykresu zależności lepkość właściwej od stężenia przeprowadzamy stosując wiskozymetr kapilarny Ubbelohde'a. Jego działanie jest oparte na prawie Poiseuila'e(strona 98 Kędzia).
Pomiar lepkości względnej cieczy polega na mierzeniu czasu t0 (zero) przepływy przez kapilarę wiskozymetru cieczy wzorcowej o objętości zawartej pomiędzy kreskami A i B oraz czasu t przepływu przez kapilarę cieczy badanej o tej samej objętości. Opierając na prawie Poiseuila'e oraz uwzgleniajac że objętości cieczy badanej i wzorcowej są równe, możemy zapisać:
(strona 105 Kędzia; wzór jest bez numeru),
następnie po przekształceniu powstania nam
(wzór 10.8; ta sama strona).
Dzięki swojej konstrukcji wiskozymetr zapewnia że na końcu kapilary podczas pomiarów tworzy się „wiszący poziom” dzięki czemu Δp powodujące przepływ cieczy nie zależy od ilości cieczy znajdującej się w wiskozymetrze, a także od napięcia powierzchniowego cieczy.
Δp jest to ciśnienie hydrostatyczne:
(Δp=ρ*g*h, Δp0(zero)=ρ0*g*h)
Ostateczny wzór na wyliczenie lepkości względnej przy pomiarach tym wiskozymetrem ma postać:
(wzór 10.9 strona ta sama)
jeśli gęstość cieczy badanej do wzorcowej są podobne można je nie umieszczać we
wzorze
(wzór 10.10)
Obu wzorów możemy wysnuć wniosek że do policzenia lepkości względnej potrzebny jest nam czas przepływu cieczy badanej i wzorcowej.
Wybaczcie brak wzorów ale nie posiadam ani skanera anie aparatu.
Na dole jest model wiskozymetru jaki znalazłam na necie.
13.Wiskozymetr Ostwalda
Jest urządzeniem służącym do pomiaru lepkości względnej
Polega na mierzeniu czasu t zero przepływu przez kapilarę wiskozymetru cieczy wzorcowej o konkretnej objętości ( zawartej pomiędzy punktami A i B) oraz czasu przepływu przez kapilarę cieczy badanej o tej samej objętości
Możemy ją wyliczyć ze wzoru:
Można go otrzymać z zapisanego dwukrotnie Prawa Pouseulle'a dla cieczy wzorcowej i dla cieczy badanej oraz porównując strony tych równań.
12.Wiskozymetr rotacyjny
Jest urządzeniem służącym do badań cieczy nienewtonowskich i określania krzywej płynięcia czyli zależności naprężenia ścinającego od szybkości ścinania (D).
Wartość
obliczamy ze wzoru:
gdzie:
to lepkość pozorna dla badanej cieczy przy rosnących i malejących szybkościach ścinania.
D to szybkość ścinania
Wartości kolejnych naprężeń ścinajacych możemy obliczyc ze wzoru:
(Z odczytujemy z odpowiednich tabel dołączonych do wiskozymetru).
14. Wiskozymetryczny pomiar masy cząsteczkowej biopolimeru.
Ustaloną na podstawie doświadczeń zależność granicznej liczby lepkościowej roztworu polimeru od jego masy cząsteczkowej przedstawia wzór :
[η] = K × Mα
gdzie: K-stała zależna od rodzaju polimeru i rozpuszczalnika
α - współczynnik zależny od kształtu makrocząsteczki polimeru w roztworze
Wartość stałych K i są określane na podstawie pomiaru masy molowej polimeru metodą rozpraszania światła lub metodą sedymentacji.
Po zlogarytmowaniu wyżej wymienionego wzoru otrzymujemy:
Log M=1/α (log[η]-logK)
Wiskozymetryczny pomiar masy cząsteczkowej polega na wyznaczeniu granicznej liczby lepkościowej roztworu badanego polimeru ([η]=lim ηwł/c) i wyliczeniu masy cząsteczkowej z wyżej wymienionego wzoru.
15. Metoda Stokesa
Metoda Stockesa polega na pomiarze prędkości opadania kulki w badanej cieczy. Na kulkę działają 3 siły:
siła ciężkości skierowana pionowo w dół, wyrażana wzorem
P = m*g = V*ρ*g = 4/3 πr3 *ρ *g
siła wyporu hydrostatycznego skierowana do góry, wyrażana prawem Archimedesa
Q = V* ρc*g = 4/3 πr3 * ρc*g
siła tarcia wewnętrznego ( oporu lepkości ), skierowana ku górze, wyrażana prawem Stockesa
R = 6πr*η*v
gdzie: Q R
m-masa kulki
V-objętośc kulki h
g-przyspieszenie ziemskie
ρc-gęstośc cieczy P
ρ-gęstośc kulki
r-promień kulki
η-lepkośc cieczy
v-prędkośc kulki
Początkowo kulka opada ruchem przyspieszonym, gdyż siła ciężkości kulki jest większa od sumy sił wyporu i lepkości. Zgodnie ze wzorem Stockesa, wzrost prędkości (v) kulki powoduje wzrost sily lepkości (R). Przy odpowiednio wysokiej prędkości zachodzi równośc:
P = Q + R
Od tej chwili kulka porusza się ruchem jednostajnym ze stałą prędkością. Podstawiając odpowiednie wartości sił do powyższego wzoru otrzymamy:
4/3 πr3 *ρ *g = 4/3 πr3 * ρc*g + 6πr*η*v
po przekształceniu otrzymamy:
η = 2r2 * g( ρ - ρc ) / 9v
Prędkośc opadania kulki otrzymujemy z czasu opadania kulki (t) i długości przedziału w którym ten czas mierzymy (h).
16. Rodzaje Lepkości
Lepkośc możemy wyliczyc z prawa Newtona ( patrz pytanie nr 17 ):
η = ( F*Δx)/(S*Δv)
Jest to siła niezbędna do utrzymania różnicy prędkości 1 m/s między dwiema warstwami cieczy o powierzchni 1 m2, przesuwającymi się względem siebie w odległości 1m. Jednostką lepkości jest N*s/ m2, używana jest też jednostka zwana puazem:
P = 0,1 N*s/ m2
Lepkośc względna to stosunek lepkości danej cieczy do lepkości cieczy wzorcowej w najczęstszym przypadku wody, a w przypadku roztworu jest do lepkości czystego rozpuszczalnika. Jest wielkością bezwymiarową.
[ η'] = η/ η0
Lepkośc właściwa także jest wielkością bezwymiarową definiowaną wzorem:
ηwł = η/ η0 - 1
Stosunek lepkości właściwej do stężenia (c) rozpuszczonego składnika przy tymże stężeniu dążącym do zera i prędkości ścinania (u) dążącej do zera, nazywamy lepkością graniczną:
[η] = limc-->0 u-->0 (ηwł/c)
Jednostką granicznej liczby lepkościowej jest cm3/g ( odwrotnośc stężenia ).
Wartości granicznej liczby lepkościowej odczytujemy z wykresu funkcji ηwł/c = f (c) poprzez ekstrapolację otrzymanej prostej do stężenia zerowego :)
ηwł/c
0 c
Posiadając wartośc granicznej liczby lepkościowej możemy wyliczyc masę dowolnych biopolimerów ( patrz pytanie 14 ).
17. Prawo Newtona, jednostki
Prawo newtona: Siła F wprowadzająca ciecz w ruch jest proporcjonalna do powierzchni S poruszających się względem siebie warstw cieczy oraz do spadku prędkości ∆V/∆x czyli:
F=Sη (∆V/∆x)
η - współczynnik lepkości (lepkość)
Jednostki lepkości: [η]=Ns/m²= kg/ms
Jednostka spoza układu Si: zwana Puazem ( P) 1P=10 ¹̄ Ns/m²
18. Reologia, wielkości, definicje
Reologia- obejmuje zagadnienia dotyczące odkształcenia i przepływu materii- czyli ruchu jednych elementów ośrodka względem innych. Przepływ cieczy lepkiej jest jednym ze specjalnych przypadków odkształcenia postaci materii.
Oddziaływania występujące w przepływających płynach można charakteryzować podając naprężenia styczne: τ = F/S , jako funkcję prędkości ścinania (u=dv/dx).
Wykres τ=f(u) nazywamy krzywą płynięcia. Różnicuje ona płyny na dwie kategorie: newtonowskie i nienewtonowskie. Dla pierwszej kategorii wykresem jest linia prosta przechodząca przez początek układu współrzędnych dla drugiej kategorii linia nie przechodzi przez początek.
Iloraz : τ/u jest lepkością płynu (η)
Rodzaje lepkości:
Lepkość względna i jej definicja: [η̕]=η/η₀
Lepkość właściwa Definicja: ηwł= (η/η₀)-1
Lepkość graniczna Definicja:
L. względna i właściwa- bezwymiarowe wielkości
L. graniczna- oznacza ηwł/c przy stężeniu c oraz u zmierzających do 0. Wyznaczamy ją z granicznej zależności: ηwł/c=[η] + k[η] gdzie k- stała Huggina
19. Ciecze newtonowskie i nienewtonowskie, podziały
Dla płynów newtonowskich lepkość nie zależy od szybkości ścinania, zależy natomiast od własności substancji tworzącej płyn i jego parametrów termodynamicznych takich jak temperatura i ciśnienie. Istnieją płyny, zwane płynami nienewtonowskimi, które nie spełniają powyższej zależności, dla nich naprężenia nie są proporcjonalne do gradientu prędkości, co jest równoznaczne z tym, że współczynnik lepkości nie jest stały lecz jest funkcją gradientu prędkości. Zależność naprężeń od gradientu prędkości przedstawiona na wykresie nosi nazwę krzywej płynięcia. Dla płynu newtonowskiego krzywa płynięcia jest prostą przechodzącą przez początku układu współrzędnych.
Krzywa płynięcia dla płynu newtonowskiego
Jeżeli krzywa płynięcia jakiegoś płynu nie jest prostą przechodzącą przez początek układu współrzędnych płyn taki jest płynem nienewtonowskim, lecz płynem z granicą płynięcia. Płyn newtonowski można też traktować jako specjalny przypadek płynu nienewtonowskiego.
20. Ciecze tiksotropowe
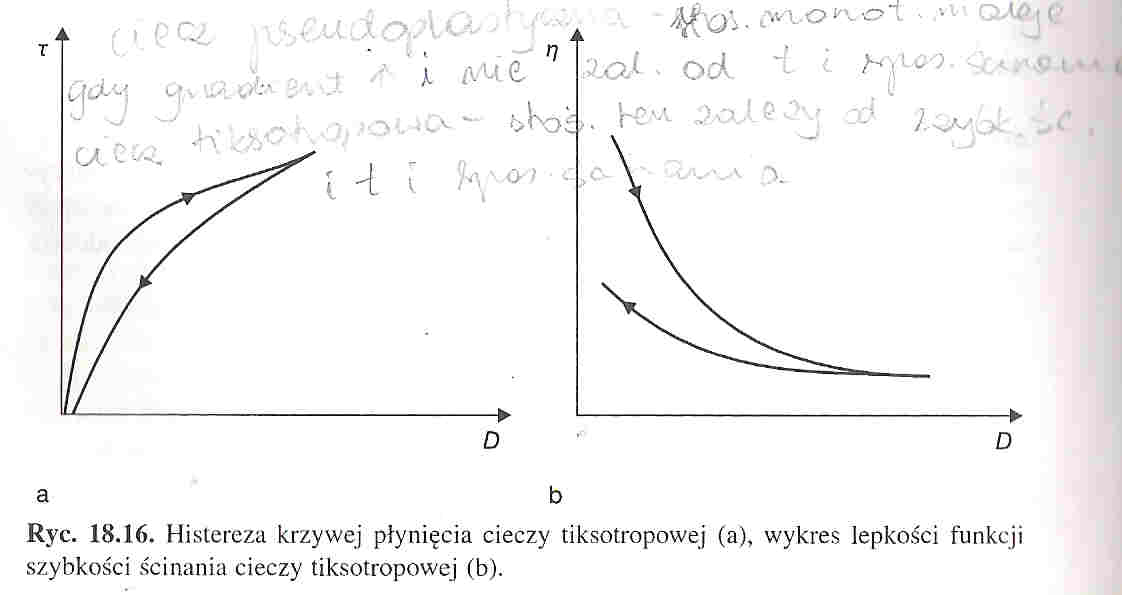
W cieczach tiksotropowych stosunek naprężenia ścinającego do gradientu prędkości zależy od szybkości, czasu i sposobu ścinania. Dla cieczy tiksotropowej krzywa płynięcia(wykres zależności naprężenia ścinającego od szybkości ścinania) wykazuje histerezę. Właściwości tiksotropowe krwi są związane z tworzeniem struktur w warunkach braku ścinania oraz i rozpadaniem się w obecności naprężeń ścinających. Dzięki temu badania krzywych płynięcia i ich analiza pozwalają wyciągnąć wnioski na temat rozmiarów struktur, łatwości ich tworzenia i warunków w jakich ulegają rozpadowi. Właściwości tiksotropowe krwi związane są z tworzeniem i rozpadaniem skupisk krwinek czerwonych. Zjawisko to nazywa się agregacją krwinek czerwonych. Odtwarzanie struktur odbywa się w bardzo krótkim czasie, w związku z tym histereza krzywej płynięcia jest prawie niezauważalna.
21. Ciecze pseudoplastyczne
Cieczami pseudoplastycznymi nazywa się ciecze w których stosunek naprężenia ścinającego do gradientu prędkości w określonych warunkach temperatury i ciśnienia nie jest stały. Może on także monotonicznie maleć wraz ze wzrostem gradientu prędkości lecz nie zależeć od czasu i sposobu ścinania. Taką ciecz jest między innymi krew.
22. Wzór Einsteina na lepkość
Wzór Einsteina określa lepkość względną roztworu, w Którym cząsteczki substancji rozpuszczonej mają kształt kulisty.
Gdzie:
Φ=
- współczynnik objętościowy roztworu; Vc-objętość cząsteczek substancji rozpuszczonej, Vr- objętość całkowita roztworu
η lepkość roztworu
η.-lepkość rozpuszczalnika
Objętość cząsteczek substancji rozpuszczonej jest równa iloczynowi liczby n moli tej substancji, liczby Avogadra NA i objętości V jednej cząsteczki:
Φ
Jeżeli uwzględnimy że M=
zaś c=
to powyższy wzór będzie wyglądał:
Φ
23. Akumulacja osiowa, efekt Magnusa
- Akumulacja osiowa polega na tym, że krwinki gromadzą się bliżej osi naczynia unikając jego ścian.
- Powstawanie akumulacji osiowej tłumaczy się efektem Magnusa (na ciało wykonujące ruch obrotowy i poruszające się ruchem postępowym działa siła prostopadła do tego ruchu powodująca odchylenie).
- Ruch obrotowy wywołujący efekt Magnusa (a co za tym idzie akumulację krwinek) powstaje w skutek wytworzonego gradientu prędkości (powstaję on ze względu na to, że bliżej ścianek naczynia warstwy płynu poruszają się wolniej). Ruch obrotowy pociąga za sobą ciecz nadając jej ruch cyrkulacyjny wokół krwinki, co jest powodem rozrzedzenia linii prądu przy odściennej stronie krwinki a zagęszczenie ich od strony odosiowej. W ten sposób wytwarza się różnica ciśnień, która znosi krwinkę do osi przewodu.
- Akumulacją osiową krwinek tłumaczy się zależność lepkości krwi od prędkości przepływu.
- W warunkach fizjologicznych krew zachowuje się jak ciecz newtonowska i lepkość prawię nie zależy od prędkości przepływu, jednakże akumulacja osiowa powoduje, że lepkość jest mniejsza (warstwa cieczy między ścianą a strumieniem krwinek zmniejsza tarcie)
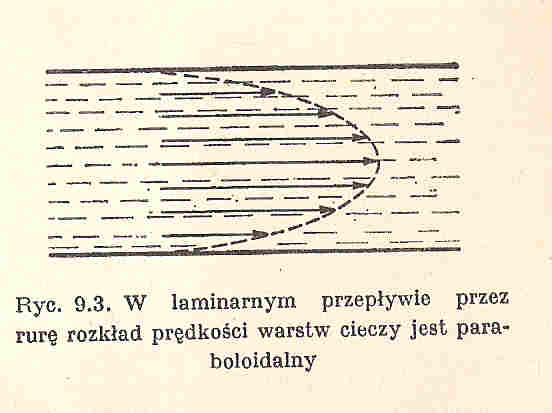
24. Przepływ laminarny
Przepływ laminarny (warstwowy) - jest to taki rodzaj przepływu płynu lepkiego, w którym największą prędkość ma ciecz poruszająca się wzdłuż osi przewodu, a ciecz przy ściance pozostaje nieruchoma (występuje gradient prędkości wywołany tarciem wewnętrznym <<lepkością>>). Zachodzi dla małych prędkości przepływu, gdy liczba Reynoldsa nie przekracza tzw. wartości krytycznej (powyżej której przepływ staje się turbulentny).
Objętość V cieczy przepływającej laminarnie w czasie t przez poprzeczny przekrój rurki włoskowatej o promieniu r i długości l, na końcach której panuje różnica ciśnień Δp jest określana prawem Poiseuille'a (które wykorzystujemy w pomiarze współczynnika lepkości).
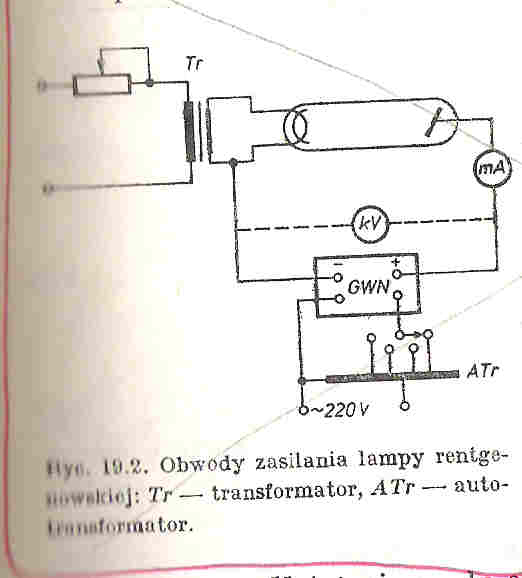
25. Budowa lampy rentgenowskiej i 26. Wytwarzanie promieni rentgenowskich
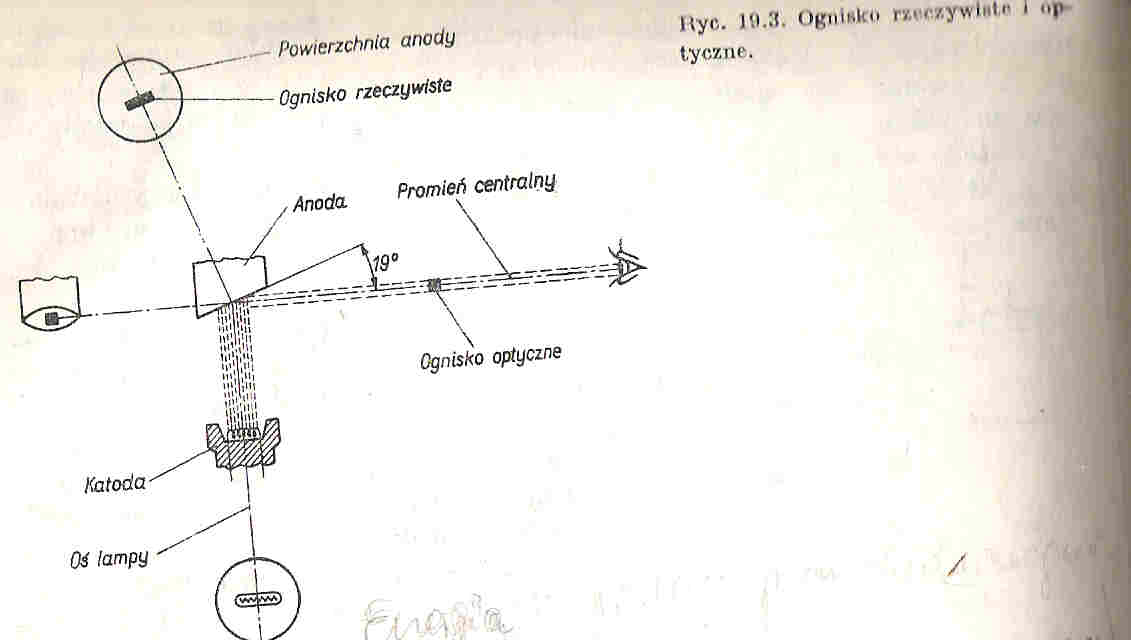
Działanie lampy rentgenowskiej opiera się na wykorzystaniu elektronów o wysokich energiach kinetycznych zaś uzyskanie promieniowania rentgenowskiego jest możliwe dzięki hamowaniu tych elektronów na anodzie lampy rentgenowskiej.
Lampa rentgenowska zbudowana jest z Katody (umieszczonej w czaszy ogniskującej) najczęściej wolframowej na, której na wskutek przyłożonego napięcia (ok. 10V) na drodze termoemisji wytwarzane są elektrony. Ilość emitowanych elektronów może być regulowana za pomocą umieszczonego w obwodzie katodowym opornika zmiennego, którym można regulować rozżarzenie katody.
Elektrony uzyskują wysoką energię kinetyczną w silnym polu elektrycznym, które powstaje dzięki przyłożonemu napięciu (od kilku do kilkuset tysięcy Volt), uzyskiwane dzięki generatorowi wysokich napięć (GWN), a następnie są ogniskowane za pomocą czaszy ogniskującej na anodzie w ognisku rzeczywistym.
Odbywa się tam zjawisko polegające na tym, że pola elektryczne jąder atomów anody działaj na wysokoenergetyczne elektrony co prowadzi do ich zahamowania. Podczas tego procesu 99% energii elektronów ulega rozproszeniu w postaci ciepła . Pozostała energia jest oddana w postaci promieniowania rentgenowskiego.
*Jeśli elektron ulegnie najpierw kilku zderzeniom niesprężystym to część energii traci podczas tych zderzeń.
*jeśli elektron straci całą energie podczas jednego gwałtownego hamowania to cała ta energia zostaje zamieniona na energie fotonu rentgenowskiego
Ognisko rzeczywiste - nazywamy miejsce na anodzie na które pada strumień elektronów.
Ognisko optyczne - nazywamy rzut ogniska rzeczywistego na płaszczyznę prostopadłą do przebiegu wiązki promieniowania elektromagnetycznego.
* rozmiary ogniska optycznego mają istotny wpływ na ostrość aparatu rentgenowskiego co jest ważne w lampach diagnostycznych
27. Powstawanie promieniowania rentgenowskiego, widmo ciągłe
Elektrony przyspieszone w silnym polu elektrycznym miedzy katoda, a anoda, przenikają w pobliże jader atomowych anody i pod działaniem pola elektrycznego atomu zostają zahamowane, uwalniając przy tym energie w postaci promieniowania elektromagnetycznego, o długości fali zależnej od wartości energii kinetycznej elektronu w okresie hamowania. Energia ta zależy od tego czy elektron straci od razu energie w procesie gwałtownego hamowania, czy najpierw dozna kilku zdarzeń niesprężystych z atomami anody, tracąc przy tym cześć energii, a po tym zostanie dopiero zahamowany. W tym pierwszym przypadku cala energia kinetyczna elektronów zostaje zamieniona na energie fotonu rentgenowskiego, dlatego promieniowanie emitowane przez lampę rentgenowska ma widmo ciągłe, czyli jest szerokim pasmem fal elektromagnetycznych o rożnych energiach i długościach fal. Rozkład energii widma jest na wykresie. Cechy charakterystyczne widma ciągłego:
1.istnienie ostrej granicy od strony fal krótkich. Związane z tym jest prawo Duane'a i Hanta,
U- napięcie anodowe
e- nabój elektronu
ν - częstość drgań krótkofalowej granicy widma
maksymalne ν otrzymamy gdy cala energie wypromieniowana zostanie w jednym fotonie. Max częstotliwość związana jest z minimalna w danym widmie długością fali, którą można otrzymać ze wzoru:
po podstawieniu h, c, i e otrzymuje się:
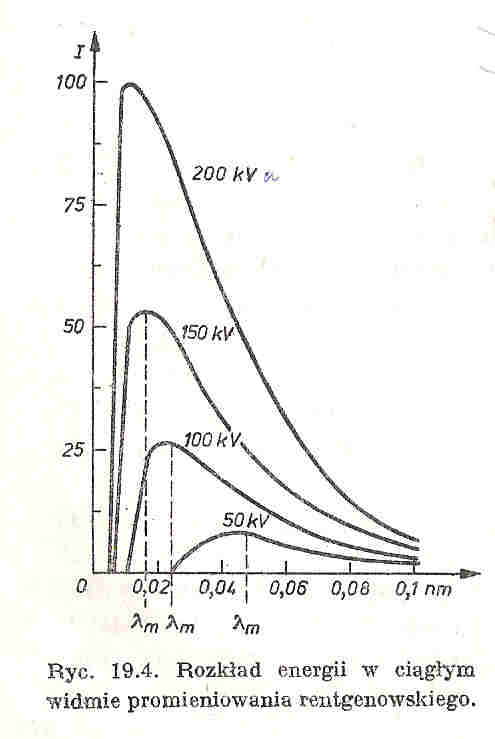
2. Gwałtowny wzrost natężenia promieniowania w miarę wzrostu napięcia anodowego, natężenie to jest proporcjonalne do kwadratu napięcia:
gdzie:
C - stała
Z - liczba atomowa materiału anody
i - natężenie prądu anodowego
U - Napięcie anodowe
28. Widmo charakterystyczne.
Na tle widma ciągłego występują wyraźne linie widmowe charakterystyczne dla pierwiastka, z jakiego jest zbudowana anoda. Powstaje wówczas, gdy energie elektronów przekroczy pewna konkretna wartość, która zależy od pierwiastka hamującego, wtedy spowoduje to przesuniecie sie elektronów orbitalnych atomów anody na wyższe poziomy energetyczne i powracając do stanu podstawowego emitują kwanty promieniowania rtg o energiach charakterystycznych dla danego pierwiastka. Są to głownie linie serii K i L, w przypadku cięższych pierwiastków M i N.
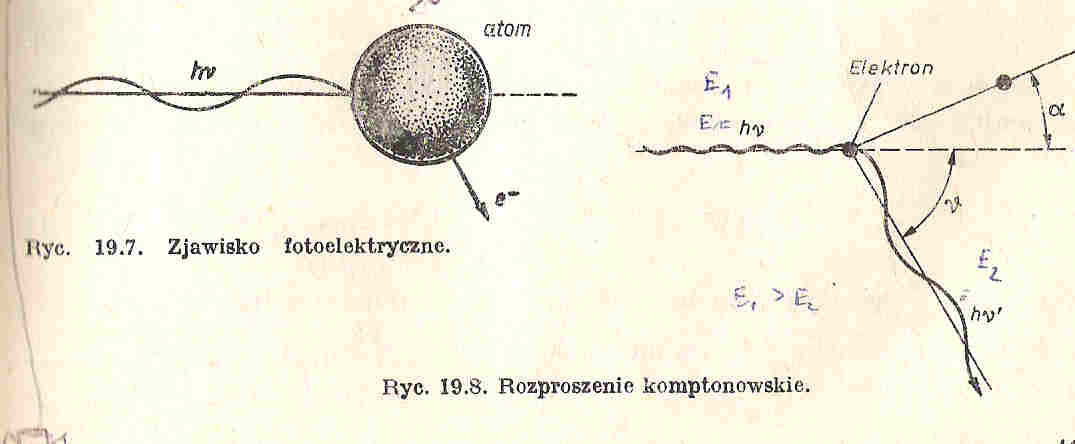
29. Zjawisko fotoelektryczne.
Zachodzi, gdy z atomu pod wpływem fali elektromagnetycznej zostaje wybity elektron, foton nadaje elektronowi energię kinetyczną 1/2mv2.
Energia fotonu hv zostaje zużyta na wykonanie pracy W potrzebnej do przezwyciężenia energii wiązania elektronu (praca wyjścia) oraz na nadanie elektronowi energii kinetycznej.
hv= W + 1/2mv2
Atom pozbawiony elektronu staje się jonem dodatnim. Wybity elektron to fotoelektron.
30 . Rozproszenie Comptonowskie.
Wynik sprężystego zderzenia fotonu z elektronem. Po zderzeniu foton zostaje odrzucony, a foton rozproszony. Elektron uzyskuje pęd p=mv, a foton rozproszony ma mniejszą częstotliwość od fotonu padającego. Związany jest z tym przyrost długości fali.
Ponieważ¿ zderzenie fotonu z elektronem jest sprężyste, podlega zasadzie zachowania pędu:
oraz zasadzie zachowania energii:
-długość fali Comptona
31. Tworzenie par elektron-pozyton
Zjawisko to zachodzi w polu jądra atomowego i polega na wyzwoleniu przez foton dwóch elektronów o przeciwnych ładunkach elektrycznych-negatonu i pozytonu, przy jednoczesnym jego unicestwieniu(fotonu).Proces ten jest możliwy jedynie wtedy, gdy energia fotonu przekracza energie równoważna masie spoczynkowej dwóch elektronów, czyli musi być większa niż. 1,022MeV (E jednego elektronu=0,511MeV). Przekaz energii i pędu zachodzi za pośrednictwem jądra atomowego lub elektronu.
hν=2 m0c2+Ek+ +Ek-
Ek- to energia kinetyczna elektronu Ek+ to energia kinetyczna pozytonu
Powstałe elektrony jonizują inne atomy kosztem swej energii kinetycznej. Pozyton po utracie energii łączy sie z negatonem, po czym oba elektrony ulęgają samounicestwieniu a na ich miejscu powstają 2 fotony.
32. Prawo osłabienia, współczynnik μ, warstwa połowiąca
Prawo osłabiania:
Mechanizmy oddziaływania promieniowania elektromagnetycznego z materia powodują, że wraz ze wnikaniem wiązki promieniowania w głąb środowiska, jej natężenie maleje w wyniku absorpcji i rozproszenia części fotonów. Spadek natężenia jest wyrażony prawem osłabiania, które głosi, że względne osłabianie natężenia promieniowania dI/I jest proporcjonalne do przyrostu grubości dx substancji pochłaniającej.
dI/I= - μdx
a po scałkowaniu:
I=I0 e-μx (I0- natężenie wiązki padającej; I- wiązki po przejściu warstwy o grubości x)
gdzie: μ -współczynnik osłabiania, jego wartość zależy od masy właściwej absorbentu i długości fali promieniowania
Warstwa połowiąca:
Warstwa połowiąca d - grubość warstwy danego materiału powodująca
zmniejszenie o połowę natężenia przechodzącej przez nią wiązki
promieniowania. Odgrywa ona wazna role przy ocenie przenikliwosci promieniowania w radioterapii.
0.5I0=I0e-μd
μd=lg2/lge=0.693
d=0.693/ μ
34. Działanie promieniowania jonizującego z materią
Oddziaływanie promieniowania jonizującego na materię sprowadza się głównie do jonizacji, będącej następstwem niesprężystych oddziaływań cząstek jonizujących z elektronami i jądrami atomów absorbentu. Jonizacja właściwa charakteryzuje zdolność jonizowania danego promieniowania. Jej miarą jest liczba par jon+elektron wytworzonych wzdłuż jednostki drogi cząstki jonizującej.
Cząstki jonizujące mogą powodować także wzbudzenie atomów lub cząsteczek (przeniesienie ich na wyższy poziom energetyczny, co jest związane z przesunięciem elektronów na orbitalach). Cząsteczki wzbudzone powstają bezpośrednio w wyniku zderzeń niesprężystych z cząstką jonizującą lub w wyniku jonizacji z natychmiastowym zobojętnieniem jonu: M M++ e- M*
Stany wzbudzone cząsteczek są nietrwałe, a powrót do stanu podstawowego może realizować się następującymi sposobami:
Nadmiar energii zostaje oddany w postaci promieniowania luminescencji,
Energia wzbudzenie zostaje zużyta na dysocjację cząsteczki,
Energia wzbudzenia jest przeniesiona na inną cząsteczkę poprzez bezpośrednie zderzenie lub rezonans.
Ciężkie cząstki naładowane (protony, deuterony, cząstki α) współdziałają z materią w następujących procesach:
Niesprężyste zderzenia z elektronami powłok atomów.
Reakcje jądrowe,
Sprężyste zderzenia z atomami lub jądrami atomów.
Rola każdego z tych procesów zmienia się w zależności od typu cząstki i jej energii. Nasilenie wywołanej jonizacji zależy od ładunku cząstki i jej masy. Gęstość jonizacji wzrasta w miarę zbliżania się cząstki do końca jej toru, gdzie następuje gwałtowny zanik jonizacji.
Elektrony działają na materię w odmienny sposób, co jest spowodowane ich małą masą. Mogą one bezpośrednio oddziaływać z polem elektrycznym jąder atomowych w sposób sprężysty lub niesprężysty. W pierwszym przypadku jądra absorbentu nie zyskują energii elektronów, natomiast w drugim ją pochłaniają.
Promieniowanie elektromagnetyczne (fotony): Oddziaływanie jonizacyjne fotonów z materią może być realizowane trzema mechanizmami: efektu fotoelektrycznego, zjawiska Comptona oraz zjawiska tworzenia się par elektron-pozyton. W ich wyniku powstają elektrony, zwane wtórnymi, które całkowicie lub częściowo przejmują energię fotonów. Są one właściwym czynnikiem jonizującym. Udział tych trzech procesów jest różny w zależności od energii fotonów, np. dla energii 10 keV zjawisko udział zjawiska fotoelektrycznego wynosi 99%, dla 2 MeV udział zjawiska Comptona wynosi 99%, a dla 20 MeV zjawisko Comptona i powstawanie par stanowią po 50% zachodzących procesów oddziaływania.
Neutrony mogą oddziaływać na materię na trzy sposoby:
Zderzenia sprężyste z jądrami atomów absorbentu. Suma energii kinetycznych rozproszonego neutronu i jądra absorbentu (jądro odskoku) po zderzeniu muszą być równe energii neutronu przed zderzeniem. W tkankach jądrami odskoku są zazwyczaj jądra tlenu, azotu, węgla i wodoru. Jądra wodoru w pewnych przypadkach mogą przejmować całkowitą energię neutronu. Neutrony nie jonizują więc materii bezpośrednio, lecz za pośrednictwem protonów.
Zderzenia niesprężyste. Część energii neutronu jest przekazana na wzbudzenie jąder absorbentu. Jądra te powracając do stanu podstawowego emitują kwanty γ.
Wychwyt neutronu przez jądra absorbentu. W procesie tym biorą udział głównie neutrony termiczne (znajdujące się w równowadze termicznej ze środowiskiem). W tkankach w procesie wychwytu biorą udział głownie jądra wodoru, fosforu i azotu. Dochodzi do przekształceń tych jąder np. 1H (n,p) 2H.
35: Dawki promieniowania jonizującego, jednostki, dawki graniczne, przykłady.
Wyróżniamy następujące dawki promieniowania jonizującego:
1. Dawka pochłonięta D określona wzorem D=E/m -jes to stosunek energii przekazywanej przez promienie jonizujące danemu elementowi masy m substancji przez masę m.
Jednostka: [1Gy]=1J/kg (Gy-grej)
W użyciu bywa też inna jednostka: 1rd (rad) 1rd=0,01J/kg
2. Dawka ekspozycyjna X określona wzorem X=Q/m -jest to suma ładunków elektrycznych jonów jednego znaku wytworzonych przez promieniowanie w jednostce masy powietrza m.
Jednostka: [X]=C/kg
W użyciu bywa też inna jednostka spoza układu SI 1R (rentgen) 1R=2,58*10^-4 C/kg
Ad 1,2 -stosujemy przyrosty dla m, E i Q dlatego iż pole promieniowania obszaru który nas interesuje (badany obiekt) jest niejednorodne.
3. Moc dawki pochłoniętej D jest to iloraz przyrostu dawki przez wartość czasu, w których przyrost następuje.
Określa ją wzór: D="delta"D/"delta"t
Jednostka: [D]=1Gy/s lub 1rd/s
Moc dawki ekspozycyjnej X="delta"X/"delta"t
Jednostka: [X]=1C/s lub 1R/s
4. Równoważnik dawki pochłoniętej H określa implikacje biologiczne spowodowane ekspozycją na promieniowanie przy małych wartościach dawek pochłoniętych.
Określony wzorem: H=D*Q*N
Jednostka: 1siwert 1Sv=PJ/kg używana jest także jednostka 1rem gdy D jest wyrażone w radach, czyli: 1Sv=1000rem
5. Efektywny równoważnik dawki Hef -ma zastosowanie w ocenie prawdopodobieństwa przypadku zgonu lub prawdopodobieństwa wystąpienia poważnych skutków dziedzicznych w dwóch pierwszych pokoleniach.
Określony jest wzorem:
36. Efektywny równoważnik dawki Hef
Wielkość ta jest wskaźnikiem pomocnym w ocenie prawdopodobieństwa przypadku zgonu(jako skutku somatycznego) lub prawdopodobieństwa wystąpienia poważnych skutków dziedzicznych w dwóch pierwszych pokoleniach.potrzeba wprowadzenia takiego wskaźnika wynika z tego że wra żliwość na promieniowanie różnych tkanek i organów dla takich samych równoważników dawek jest różna.
Hef=ΣT WTHT
gdzie:
HT-ŚREDNI równoważnik dawki w tkance lub organieT
WT-współczynnik wagi,wyrażający stosunek prawdopodobieństwa wystąpienia skutku somatyczno-stochastycznego wywołanego napromienieniem tkanki(organu) T do prawdopodobieństwa wystąpienia tego skutku przy równomiernym napromienieniu całego ciała
37. LET
LET (Linear Energy Transfer, liniowe przenoszenie energii) jest wielkością charakteryzującą zdolność jonizowania danej substancji, mierzona ilością energii oddanej przez cząstkę jonizującą na jednostkę drogi:
LET=E/x
Inna wielkością opisującą zdolność jonizowania jest jonizacja właściwa, której miarą jest liczba par jonów (jon + elektron) wyzwolonych wzdłuż jednostki drogi cząstki jonizującej
n/x.
LET lepiej obrazuje zjawisko wydatkowania energii gdyż cząstki jonizujące tracą swą energię nie równomiernie ale porcjami.
Między jonizacją właściwa i LET zachodzi związek:
E/xW = n/x
W- średnia energia, którą promieniowanie traci na wytworzenie jednej pary jonów (dla powietrza W= 34eV)
Wartość E/x zależy od wielu czynników
ładunku cząsteczki Ze (Z - liczba ładunków elementarnych, e - ładunek elementarny)
prędkości cząsteczki v
E/x (ZE)2/v2
LET jest wielkość odwrotnie proporcjonalną do kwadratu prędkości cząstki (cząstka dłużej przebywa w rejonie elektronu orbitalnego przez co prawdopodobieństwo oddziaływania z elektronem jest większe)
Polecam obejrzeć tę prezentację: http://www.biofizyka.amp.edu.pl/RADIOTERAPIA-MT-2009-studenci.pdf
38. Efekt biologiczny promieni jonizujących
z punktu widzenia biofizyki dwie właściwości wyróżniają promieniowanie jonizujące spośród czynników fizycznych
1. Niewspółmiernie intensywne działanie biologiczne stosunkowo bardzo małej ilości energii doprowadzonej do organizmu za pośrednictwem promieniowania jonizującego. Dawka śmiertelna dla człowieka w przypadku napromieniowania całego ciała wynosi ok. 600rad, co odpowiada 6 dżulom lub 1,4 kalorii. Ta mała energii jest biologicznie bardzo aktywna. Prawdopodobnie wiąże się to z tym, że pierwotne reakcje popromienne zachodzą w małych objętościach o rozmiarach cząsteczek i makrocząsteczek. Poza tym w warunkach żywego organizmu początkowe niewielkie uszkodzenie ulega zwielokrotnieniu (potencjalizacja uszkodzenia).
2. Każdy czynnik patogenny dowolnego pochodzenia (chemiczny, toksyczny, farmakologiczny, itp.) działa biologicznie dopiero po przekroczeniu charakterystycznej dlań wartości progowej. Powyżej tej wartości intensywność działania szybko wzrasta, aż do osiągnięcia wartości bezwzględnie śmiertelnej. W przeciwieństwie do tego promieniowanie jonizujące często cechuje się brakiem dawki progowej (np. dla uszkodzeń genetycznych), a oprócz tego różnica między nią a dawką śmiertelną może być bardzo duża. Fakt ten świadczy o istnieniu dużych różnic wrażliwości na promieniowanie między składnikami napromieniowanej populacji.
Efekt promieniowania ujawnia się w miejscu absorpcji tego promieniowania. Można je wtedy interpretować na podstawie tzw. Teorii trafień i teorii tarczy. Punktem wyjścia obu teorii jest stwierdzenie, że absorpcja promieniowania w materii nie jest procesem ciągłym, lecz kwantowym oraz podporządkowanym prawom statystyki.
Z matematyczny rozważań tego stwierdzenia wynika, że efekt biologiczny po napromieniowaniu jednorodnej populacji biologicznej (np.komórki w hodowli in vitro, kolonia drobnoustrojów, roztwór biocząsteczek, np. DNA itp.) ujawni się w statystycznym składniku tej populacji(komórka, bakteria cząsteczka DNA itp.) tylko wówczas,gdy w składniku tym znajdzie się określona minimalna ilość „trafień”, czyli pojedynczych aktów absorpcji promieniowania. Umiejscowienie trafień nie może być przy tym dowolne. W każdym żywym organizmie istnieje jedna lub kilka „wrażliwych objętości” lub „tarcz”, w których musi nastąpić określona ilość aktów absorpcji (trafień), aby efekt popromienny mógł się ujawnić.
Natura „tarcz” reprezentowanych przez liczbę ekstrapolacyjną nie jest dokładnie znana. Są dowody na to, że SA one zlokalizowane w jądrze komórkowym, przy czym cechom właściwym „tarczom” najbardziej odpowiada DNA. Liczba „tarcz” odpowiedzialnych za określoną funkcją komórki, np. reprodukcję, może być różna. Bakterie i komórki haploidalne mają jedną „tarczę” ( komórki diploidalne - więcej niż jedną. zniszczenie promieniowaniem jednej „tarczy” odpowiedzialnej za określoną funkcję powoduje wypadnięcie tej funkcji, np. komórka traci zdolność podziału.
W komórkach diploidalnych taki sam efekt można uzyskać po zniszczeniu wszystkich „Tarcz”. Jeśli pozostaje choćby jedna „tarcza”, odnośna funkcja zostaje zachowana. Uszkodzenie popromienne charakteryzujące się zniszczeniem części „Tarcz” nosi nazwę subletalnego. Po pewnym czasie „tarcze” unieczynione promieniowaniem ulegają odtworzeniu. Uważa się, że uszkodzenie subletalne dotyczy odpowiedniego odcinka tylko jednej nici DNA, a naprawa tego uszkodzenia jest realizowana na drodze syntezy sterowanej przez nie uszkodzoną komplementarną nić cząsteczki DNA. Natomiast uszkodzenie letalne dla komórki obejmuje obie nici cząsteczek DNA, co oczywiście uniemożliwia naprawę uszkodzenia.
W układach żywych nie zawsze zachodzi bezpośrednie działanie promieniowania: miejsce absorpcji energii nie musi być identyczne z miejscem ujawnienia się reakcji radiobiologicznej. w tym przypadku zachodzi pośrednie działanie promieniowania.
Za działanie pośrednio odpowiedzialne są przede wszystkim niektóre produkty radiolizy wody ustrojowej (rodniki H' , OH', HO2' oraz H2O2 i eaq). Ze względu na dużą zawartość wody działanie pośrednie odgrywa w organizmach żywych dużą rolę. Rodniki wodne mogą np. spowodować rozpad biocząsteczki na mniejsze fragmenty lub utleniając grupy SH, występujące prawie we wszystkich białkach, prowadzić do utraty lub zmiany aktywności biologicznej biocząsteczki. Rodniki wodne mogą działać biologicznie również pośrednio poprzez nadtlenki organiczne,np. rodnik OH', powstający podczas pośredniego działania promieniowania, reaguje ze związkami organicznymi według reakcji: RH+ OH' → ROO'. W obecności tlenu rodnik organiczny utlenia się: R' + O2 → ROO'.Nadtlenek organiczny staje się początkowym ogniwem reakcji radiobiologicznej.
Ważnym czynnikiem determinującym w dużym stopniu wrażliwość obiektów biologicznych na promieniowanie, a biorącym udział w pośrednim działaniu promieniowania, jest stężenie tlenu w obiekcie w chwili napromieniowania . od obecności tlenu zależy ukierunkowanie reakcji radiochemicznych w wodzie ustrojowej, np. rodnik HO2' powstaje tylko w obecności tlenu, przy czym ze względu na krótki czas trwania pierwotnych procesów radiolitycznych cząsteczek wody (rzędu 1018-1016s), istotne znaczenie ma tylko tlen obecny w czasie napromieniowania.
Eksponencjalne krzywe przeżycia przedstawiają skutki napromieniowania komórek białaczkowych myszy w warunkach beztlenowych (w atmosferze N2) i tlenowych. D37 wynosiła odpowiednio 3,6 i 1,6 Gy z czego wynika, że uwarunkowana obecnością O2 wrażliwość komórek za napromieniowanie jest około 2,3 - krotnie większa niż w warunkach beztlenowych.
Jest to fakt o dużym znaczeniu w radioterapii nowotworów. Większość guzów nowotworowych zawiera bowiem skupiska komórek niedotlenionych, czasem wręcz na pograniczu anoksji. Komórki te są względnie radioodporne, co w znacznym stopniu obniża wartość leczniczą radioterapii. Uważa się, ze właśnie od tych komórek zaczyna się ponowny rozwój nowotworu po napromieniowaniu . zapobieganie niepożądanemu oddziaływaniu hipoksji sprowadza się do :
poprawy natlenienia guza (reoksygenacja),
2) stosowania większych dawek promieniowania (nie zawsze jest to możliwe ze względuu na niebezpieczeństwo nieodwracalnego uszkodzenia tkanek zdrowych) i
3) stosowania promieniowania o wysokim LET. Im wyższy bowiem LET, tym mniejsze znaczenie ma „efekt tlenowy”. Równocześnie, ze wzrostem LET zwiększa się prawdopodobieństwo indukowania uszkodzeń letalnych w obrębie „tarcz”. Ogólnie, im większa dawka, moc dawki i LET tym większa skuteczność radioterapii. Tłumaczy to aktualne tendencje w radioterapii zmierzającej do wykorzystania strumieni cząstek o wysokich energiach i dużej zdolności jonizacyjnej (wysoki LET).
39. Efektywny okres połowicznego rozpadu izotopów promieniotwórczych podanych do wnętrza organizmu.
Radioaktywność zdeponowana w narządzie maleje w czasie dzięki dwóm procesom:
Rozpadowi radioaktywnemu z prędkością określoną stałą rozpadu λf zgodnie z równaniem:
Wydalaniu z organizmu na drodze normalnych procesów metabolicznych z prędkością określoną stałą wydalania λb zgodnie z równaniem
Oba te procesy sumują się, więc aktywność zdeponowana w tkance lub narządzie maleje z prędkością λef = λf+ λb. Korzystając z zależności λ= można zapisać:
Lub:
Tef - efektywny okres półtrwania substancji organicznej w organizmie jako funkcja rozpadu radioaktywnego i wydalania biologicznego
40. Zastosowanie izotopów promieniotwórczych do badania kinetyki przemian metabolicznych.
Badania kinetyki przemian metabolicznych są oparte na ocenie zmian aktywności źródła promieniotwórczości w czasie.
Badanie kinetyki jodu-123 w postaci 125I-:
Po dożylnym podaniu znacznika określa się jego aktywność w surowicy i w moczu, monitorując równocześnie od zewnątrz tarczycę licznikiem scyntylacyjnym. Badanie dotyczy układu trójprzedziałowego:
Powtarzane w odpowiednich odstępach czasu pomiary radioaktywności pozwalają na ocenę szybkości transferu k znacznika między składnikami układu
Badanie kinetyki technetu-99m w postaci 99mTcHO4-
Substancja wprowadzana jest dożylnie, skąd przechodzi do tkanek i narządów, wydalana jest z moczem.
Gdy za pomocą znakowanych związków jodu lub nadchlorku technetu zablokować wychwyt przez tkanki i narządy, układ ten redukuje się do składników 1 i 2, wtedy szybkość transferu k12 można obliczyć ze wzoru:
= k12*t
Znając k12 można obliczyć k13 ze wzoru
W podobny sposób bada się kinetykę związków żelaza lub bilirubiny w organiźmie
41. Metoda rozcieńczania izotopowego.
Metoda rozcieńczania izotopowego to jedna z metod analizy radiochemicznej. Opiera się na założeniu, że izotopy tego samego pierwiastka zachowują się pod względem chemicznym w identyczny sposób. Natomiast izotopy promieniotwórcze można łatwo wykryć poprzez emitowane przez nie promieniowanie.
Metoda pozwala wyznaczyć objętość lub stężenie składnika danej mieszaniny. Do wyznaczenia objętości V składnika S mieszaniny znakuje się odpowiednim izotopem objętość V₁ tej substancji. Gdy: Aktywność jednostki tej substancji wynosi A. Aktywność całkowita V₁ czyli A*V₁ musi być równa aktywności całkowitej objętości po w prowadzeniu V₁ do objętości V czyli ( V+ V₁)B (B- aktywność jednostki objętości V+V₁)
Czyli V₁*A = (V+V₁)*B
Po przekształceniu V = V₁ ( A/B - 1) gdzie A>B I V₁≥V
V = V₁ * A/B
Metoda rozcieńczania izotopowego ma zastosowanie gdy bezpośredni pomiar nieznanej objętości jest niemożliwy np. objętości krwi, chłonki, objętości krwinek czerwonych
42 - metody klirensowe
Są to badania izotopowe umożliwiające przede wszystkim pomiary przepływu krwi i
ukrwienia narządów.
Pomiar przepływu mózgowego:
Stosuje się tu Ksenon 133 - jest to radioaktywny gaz, który po wstrzyknięciu do tętnicy szyjnej dostaje się do naczyń włosowatych a następnie dyfunduje do ciał tłuszczowych. Miarą szybkości przejścia znacznika przez mózg jest krzywa oczyszczania ksenonu zmierzona nad mózgiem. W ten sposób możemy określić czy przepływ krwi przez badaną część OUN jest prawidłowy czy zaburzony.
Pomiar przepływu sercowego:
Do oceny przepływu sercowego znakuje się erytrocyty lub albuminy krwi nadtechnecjanem. Znacznik jest wstrzykiwany do żyły łokciowej po czym dokonuje się rejestracji przepływu krwi ze znacznikiem przez serce prawe, krążenie małe i serce lewe. Na podstawie uzyskanych informacjom można ustalić granice obszaru lewej komory, ruchliwość mięśnia sercowego, pojemność wyrzutową serca i czas przepływu krwi przez jamy serca.
Dzięki metodzie pefuzji mięśnia lewej komory serca talem 201 możliwe jest uwidocznienie miejsca przebytego zawału i określenie wielkości blizny pozawałowej.
Obecnie badania klirensowe przeprowadzane są za pomocą kamery scyntylacyjnej współpracującej z komputerem.
Inne przykłady badań klirenoswych:
- fitynian indu (In) - badanie wątroby, śledziony i płuc
43. Komora Wilsona i komora pęcherzykowa, działanie i zastosowanie
Komora Wilsona - W komorze Wilsona wykorzystuje się zdolność kondensacji pary wodnej na jonach wytworzonych przez cząstki naładowane. Komora ta składa się ze szklanego naczynia cylindrycznego, którego dno stanowi ruchomy tłok. Umożliwia on szybkie (adiabatyczne) rozprężenie znajdującego się w komorze powietrza z nasyconą parą wodną. W wyniku oziębienia pojawiają się kropelki rosy na jonach (ośrodkach kondensacji) tworzących się wzdłuż torów cząstek jonizujących przechodzących przez komorę. Zastosowanie bocznego oświetlenia powoduje rozproszenie światła na kropelkach rosy, dzięki czemu można obserwować ślady torów cząstek jonizujących i fotografować. Użycie pola magnetycznego w badaniach z komorą Wilsona umożliwia zakrzywianie toru cząstek. Pomiar promienia krzywizny dostarcza informacji o pędzie i masie cząstki, natomiast kierunek zakrzywienia toru pozwala określić znak ładunku cząstki. Wadą komory Wilsona jest mała zdolność hamowania cząstek, przez co duża część procesów oddziaływania cząstki z materią przebiega poza obrębem komory. Problem ten rozwiązało opracowanie komory pęcherzykowej.
Komora pęcherzykowa - w komorze tej zamieniono środowisko gazowe na ciekłe, co zwiększyło ilość oddziaływań cząstki z materią wzdłuż toru, a tym samym zdolność do hamowania cząstki. W komorze znajduje się ciecz (ciekły wodór, hel, etylen itp.) utrzymywana w stałej temperaturze. W wyniku działania urządzenia zwiększającego objętość komory, ciśnienie zmniejsza się do wartości mniejszej od ciśnienia pary nasyconej danej cieczy w panującej temperaturze. Ciecz staje się przegrzana. W wyniku przejścia cząstki jonizującej przez komorę, na powstałych jonach tworzą się pęcherzyki pary cieczy, co można zarejestrować aparatem fotograficznym. Tym samym fotografujemy podobnie jak w komorze Wilsona tory cząstek jonizujących.
Zastosowanie: Komora Wilsona i pęcherzykowa służą do obserwacji torów cząstek jonizujących. Pozwala to na badanie cząstek o wysokich energiach oraz procesów wzajemnego oddziaływania tych cząstek na siebie
44. Efekt Czerenkowa, MDD
Efekt Czerenkowa - zjawisko powstawania promieniowania widzialnego (świecenie) w przypadku, gdy naładowana cząstka porusza się w ośrodku, dla którego prędkość fazowa światła c/n (n- współczynnik załamania dla ośrodka) jest mniejsza od prędkości v poruszającej się cząstki. Promieniowanie (zwane promieniowaniem Czerenkowa) to można rejestrować za pomocą fotopowielaczy lub klisz fotograficznych. Urządzenie takie (nazwane licznikiem Czerenkowa) znajduje liczne zastosowania w badaniach fizyki jądrowej
MDD - Maksymalna dopuszczalna dawka - jest to graniczna (maksymalna) wartość mocy dawki promieniowania, którą można aplikować człowiekowi przez dowolnie długi czas bez obawy spowodowania uszkodzeń jego tkanek (moc dawki - wartość dawki promieniowania doprowadzonej do organizmu w określonym czasie np. 4Gy/min). Obecnie obowiązująca wartość MDD wynosi 2,58*10-5 C/kg na tydzień. Nie przekraczanie tej wartości chroni przed uszkodzeniami somatycznymi i ogranicza do minimum występowanie zmian o charakterze genetycznym. Zmiany te mogą dotyczyć aparatu genetycznego gamet i z tego względu ustalono dopuszczalną dawkę skumulowaną, w określonym czasie, która wynosi 1,29*10-3 C/kg/rok. Dopuszczalną dawkę skumulowaną przez organizm pracownika w dowolnym czasie można obliczyć ze wzoru Dskum.=1,29*10-3(N-18) C/kg, gdzie N- wiek pracownika w latach.
47. Scyntygraf, Scyntykamera - działanie, zastosowanie
Scyntygrafia jest metodą uzyskiwania obrazu narządów, a przede wszystkim oceny ich czynności, poprzez zastosowanie licznika scyntylacyjnego oraz niewielkiej dawki izotopu promieniotwórczego (radioznacznika). Detektor scyntylacyjny rejestruje promieniowanie, którego źródłem jest badana okolica ciała.
Scyntygrafy są aparatami, w których detektor przesuwa się nad badanym narządem ze stałą prędkością. Jego obraz drukowany jest na papierze dzięki odpowiednik pisakom. Zagęszczenie znaków jest proporcjonalne do liczny rejestrowanych impulsów. Scyntygrafia kolorowa pozwala zobrazować zmiany aktywności poprzez zastosowanie różnych barw.
Badanie scyntygraficzne trwa dość długo, dlatego służy do diagnostyki małych narządów (np. tarczycy).
Nowocześniejszych rozwiązaniem jest scyntykamera (gamma kamera). W scyntykamerze detektor jest nieruchomy. Duża głowica tego aparatu obejmuje swoim polem widzenia całość badanego narządu (wątroby, serca, mózgu, nerek), a badanie trwa znacznie krócej w porównaniu ze scyntygrafem. Wynik badania można otrzymać na błonie fotograficznej, chociaż obecnie utrwala się znacznie częściej w pamięci komputera. W obrazie komputerowym, zależnie od potrzeb, możliwa jest zmiana skal barwnych, filtrowanie, wygładzanie a przede wszystkim badanie czynności narządów. Gamma kamery ruchome (rotujące) umożliwiają uzyskanie obrazów warstwowych (tomograficznych), podobnie jak w tomografii komputerowej. Obrazy te uzyskuje się przez okrężny ruch głowicy aparatu wokół ciała pacjenta. Technika ta określana jest jako tomografia emisyjna pojedynczego fotonu (z angielskiego - SPECT).
48. Wyznaczanie dawki ekspozycyjnej metodą komory jonizacyjnej.
W celu wyznaczenia dawki ekspozycyjnej stosujemy komorę jonizacyjną. Stanowi ona pewien rodzaj kondensatora, pomiędzy którego okładki wprowadzana jest substancja promieniotwórcza. Pozwala on mierzyć natężenie promieniowania , poprzez pomiar zmiany różnicy potencjałów między elektrodami komory wywołanej działaniem promieniowania jonizującego.
W celu wyznaczenia dawki ekspozycyjnej na początku wyznaczamy wartość promieniowania tła odczytując wskazania, gdy nie jest wprowadzona ani źródło, ani absorbent, następnie wykonujemy pomiar natężenia promieniowania w układzie źródło-detektor). po wprowadzeniu do komory badanego obiektu lub jego fantomu w układzie źródło-absorbent-detektor (pomiarów dokonujemy wielokrotnie i wartości uśredniamy).
Otrzymujemy wartości średnie:
- szybkość zliczania związana z tłem
- szybkość zliczania związana z nieosłoniętym źródłem promieniowania
- szybkość zliczania związania ze źródłem przesłoniętym fantomem
Obliczamy pozorną aktywność źródła ze wzoru:
, gdzie A to aktywność źródła.
Następnie obliczamy dawkę ekspozycyjną związaną z pochłanianiem promieniowania przez absorbent:
Nr.49 Scholastyczne i niescholastyczne skutki napromieniowania
Działanie promieniowania jonizującego (rys.)
Biologiczne efekty oddziaływań promieniowania na żywy organizm dzielimy na:
Efekty somatyczne - dotyczą napromieniowanego organizmu i polegają na uszkodzeniu komórek utrzymujących procesy życiowe.
Efekty genetyczne- występują przy uszkodzeniu komórek rozrodczych odpowiedzialnych
Za przekazywanie cech dziedzicznych.
Ze względu na relacje między dawką promieniowania a efektem biologicznym skutki promieniowania dzielimy na:
Niescholastyczne (pewne)- kiedy możemy wykazać ścisły związek, zwykle liniowy, między wielkością dawki a natężeniem skutku.
Scholastyczne- jeśli możemy mówić o zależności prawdopodobieństwa wystąpienia
określonego skutku w funkcji pochłoniętej dawki promieniowania.
Efekty genetyczne promieniowania są zawsze scholastyczne, efekty somatyczne mogą być zarówno scholastyczne jak i niescholastyczne. Powstawanie jednych i drugich skutków tłumaczy się przy pomocy dwóch teorii oddziaływania promieniowania jonizującego:
Teoria „pocisku i tarczy” bezpośredniego oddziaływania.
Teoria oddziaływania pośredniego chemiczno-biologicznego.
50 Radioliza, znaczenie
Radioliza zachodzi pod wpływem działania promieniowania jonizującego. Prowadzi do zmian radiacyjnych związków biologicznie ważnych-białek, aminokwasów, enzymów, kwasów nukleinowych, polegających na inaktywacji cząsteczki. Istotne znaczenie mają zmiany radiochemiczne zachodzące w wodzie.
ETAP I
W wyniku jonizacji może zostać usunięty elektron:
- jeden z wiążących → cząsteczka rozpada się na H+ i OH lub H i OH-,
- niewiążący → powstaje jon H2O+.
Jon H2O+ z łatwością wychwytuje elektron, następuje przejściowa odbudowa cząsteczki, znajduje się ona w stanie wzbudzonym i ulega dalszemu rozpadowi na rodniki H˙ i OH˙.
H2O++e-->H2O*->H. .+OH.
Niezobojętnione jony H2O+ rozpadają się na H+ i OH-
Jony H+ reagując z elektronami dają atomy H.
ETAP II
Oprócz wolnych rodników powstają elektrony uwodnione e-(aq) → twory złożone z elektronu i grupy otaczających go cząsteczek wody. Powstają w ten sposób, że najpierw uwolnione elektrony podlegają terminalizacji ( ich energia ulega zmniejszeniu do poziomu właściwego ruchowi cieplnemu) a następnie hydratacji.
ETAP III
W końcowej fazie powstają cząsteczkowe produkty rozkładu wody w wyniku kombinacji atomów H
i rodników OH˙:
H + H→ H2
OH + OH → H2O2
W wyniku reakcji : H2O2 + OH˙ → HO2˙ + H2O. powstaje ważny w układach biologicznych rodnik HO2˙
51. Ochrona przed promieniowaniem jonizującym
W celu ochrony przed promieniowaniem jonizującym ustalono granicę bezpiecznego napromieniowania ludzi.
Jednym z parametrów charakteryzujących promieniowanie i decydującym o charakterze uszkodzenia jest moc dawki - stosunek dawki do czasu. Tą samą dawkę można doprowadzić do organizmu w różnym czasie. Im dłuższy jest czas promieniowania tym mniejsza jest moc dawki, a im mniejsza moc dawki tym mniejsze uszkodzenie żywej materii, mimo, że całkowita pochłonięta energia jest taka sama.
Ustalono również graniczną moc dawki czyli taką, którą można aplikować człowiekowi przez czas dowolnie długi bez obawy spowodowania uszkodzenia jego tkanek. Jest to maksymalna dopuszczalna moc dawki (MDD) i wynosi 2,58 × 10-5 C/kg × tydzień, przy 8-godzinnym dniu pracy. Dawka ta dotyczy osób zawodowo zatrudnionych przy źródłach promieniowania, dla ogółu ludności dawka ta ma wartość 10-krotnie niższą i wynosi 2,58 ×10-6 C/kg × rok. Utrzymywanie mocy ekspozycji na takim poziomie zapobiega powstawaniu uszkodzeń somatycznych i ogranicza możliwość wywołania zmian o charakterze genetycznym.
Wartość dopuszczalnej dawki skumulowanej w określonym czasie to 1,29 × 10-3 C/kg/rok.
Dopuszczalną dawkę skumulowaną, w dowolnie długim okresie oblicza się ze wzoru
Dskum. = 1,29 × 10-3 (N - 18) C/kg
Gdzie:
N - wiek pracownika w latach
18 - przy źródłach promieniowania można pracować dopiero po ukończeniu 18 roku życia
Promieniowanie jonizujące można również charakteryzować jako czynnik środowiskowy. Rozszerzający się zakres zastosowań promieni jonizujących sprawia, że na działanie tego promieniowania narażone są całe populacje ludzkie.
Wielkością odniesienia obciążenia populacji ze strony „cywilizacyjnych źródeł promieniowania” jest wartość tła - promieniowania jonizującego pochodzącego z przestrzeni pozaziemskiej oraz emitowanego przez naturalne radioaktywne skażenia biosfery.
Średnia wartość tła na półkuli północnej wynosi 100 - 120 mSv(milisiwertów)/rok.
Poza promieniowaniem tła istnieją źródła promieniowania stworzone przez człowieka, będące przyczyną dodatkowego promieniowania ludzi. Są to:
Źródła medyczne (promieniowanie rentgenowskie) stosowane w diagnostyce medycznej - 80-100% tła.
Opad promieniotwórczy pochodzący z doświadczalnych wybuchów jadrowych - 20-30% tła
Odpady radioaktywne w przemyśle atomowym i energetyce jądrowej - poziom nieustalony
Promieniowanie ze źródeł cywilizacyjnych obarcza populacje wartością równą wartości tla i stale rośnie. Może być to niebezpieczne ze względu na wzrost obciążenia genetycznego populacji.
Człowiek może być narażony na promieniowanie pochodzące z poza organizmu lub takie które znajduje się wewnątrz organizmu. To skąd pochodzi promieniowanie wpływa na ocenę stopnia zagrożenia i wybór sposobu ochrony.
Wewnętrzne skażenie organizmu substancją radioaktywna ma miejsce podczas stosowania otwartych źródeł promieniowania - substancji radioaktywnych w postaci płynów, gazów, aerozoli. W większości substancje te charakteryzują się wybiórczym powinowactwem tkankowym/ narządowym
35S - skóra
90Sr, 32P - kości
60Co - wątroba
131I - gruczoł tarczowy
59Fe - krwinki czerwone
Narządy te noszą nazwę krytycznych - zdeponowane w nich izotopy promieniotwórcze rozpadają się z właściwą im prędkością emitując przy tym promieniowanie. Promieniowanie γ dzięki dużej przenikalności opuszcza organizm, a β i α są pochłaniane w sąsiedztwie miejsca rozkładu, w takich warunkach narząd/tkanka mogą doznać znacznych uszkodzeń.
Możliwość usunięcia radioaktywności zdeponowanej w narządzie jest ograniczona - zachodzi dzięki procesom rozpadu radioaktywnego lub wydalania z organizmu na drodze normalnych procesów metabolicznych.
Analogicznie do MDD ustalono maksymalne dopuszczalne stężenia radioizotopów w wodzie i powietrzu (MDS). Są to aktywności, które po zdeponowaniu w narządzie krytycznym, rozpadając się całkowicie, nie obciążają go dawką, większą od dopuszczalnej.
52. Model anizotropowy kości.
Wielkości fizyczne dzielimy na skalary, wektory oraz tensory. Tensory są wielkościami bardziej złożonymi ni z tensory. Otrzymujemy je mnożąc każdy z trzech składowych jednego wektora przez trzy składowe drugiego. Przykładem tensorów są naprężenia mechaniczne oraz odkształcenia. Na rysunku poniżej zilustrowano schemat rozkładu sił działających na wycięty z materiału anizotropowego elementarny sześcian ułatwiający zrozumienie idei tensorów.
Na każdą ściankę sześcianu działają w trzech wzajemnie prostopadłych kierunkach siły, oznaczone odpowiednimi indeksami, przy czym pierwszy oznacza numer ścianki na którą działa siła, drugi - kierunek siły. Tak więc na każdą ze ścianek o powierzchni A działają po trzy siły o kierunkach wzajemnie prostopadłych. Ze względu na to, ze liczba ścianek wynosi 6, a liczba kierunków 3 otrzymujemy 3*6=18 tensorów naprężeń. Z kolei ze względu na warunek równowagi, w jakiej znajduje się rozważany element materiału, liczba naprężeń redukuje się do 9, a dalej - ze względu na symetrię - następuje dalsza redukcja liczby tensorów do 6, z których 3 mają kierunki normalne do danej powierzchni a pozostałem trzy równoległe.
Pierwsza cyfra oznacza numer ścianki, druga jej kierunek. W rezultacie otrzymujemy 6 tensorów naprężeń, przy czym i=1-6, podobnie otrzymujemy 6 tensorów względnych odkształceń sprężystych, przy czym j=1-6. Każda z sześciu składowych tensora naprężeń jest proporcjonalna do wszystkich sześciu składowych tensora odkształceń. Zatem dla materiałów anizotropowych prawo Hooke'a zapisujemy w postaci MACIERZY :
Macierz można zapisać również w postaci:
Macierz tensorów jest symetryczna względem przekątnej. tzn. cij=cji. W związku z czym dla ciał o całkowitej anizotropii liczba współczynników sprężystych redukuje się do 21, podczas gdy dla ciał izotropowych liczba ta wynosi 2; są to współczynniki związane ze sprężystością podłużną i poprzeczną. Współczynnikom tym odpowiadają odpowiednio: moduł sprężystości podłużnej E i moduł sprężystości poprzecznej G. Takie materiały jak kość, drewno itp. Są materiałami ortotropowymi. Dla tego typu materiałów liczba współczynników sprężystości cij=9. W przypadku izotropii poprzecznej liczba niezależnych współczynników sprężystości redukuje się do 5.
53. Model dźwignia - ramię.
Model zbudowany jest z dwóch dźwigni jednostronnych połączonych przegubowo oraz podwieszonych na statywie. Elastyczne cięgno C, symulując pracę włókien mięśniowych, łączy się poprzez zespół krążków z metalowym prętem, który odkształca się gdy układ jest obciążony ciężarem. Odkształcenie normalne pręta wyznaczane - w jednostkach arbitralnych au - przez czujnik C jest miarą składowej prostopadłej siły F napinającej cięgno (WAŻNY DOŁĄCZONY WYKRES CECHOWANIA z którego odczytujemy wartość siły prostopadłej w niutonach!!!) Związek trygonometryczny między siłami wyraża wzór: F= Fprostopadłe/sinβ, gdzie β jest kątem pomiędzy cięgnem a odkształcanym prętem. Śrubowym regulatorem R możemy zmieniać wartość siły F poprzez skracanie lub wydłużanie cięgna s, które odczytuje się z odpowiedniej skali.
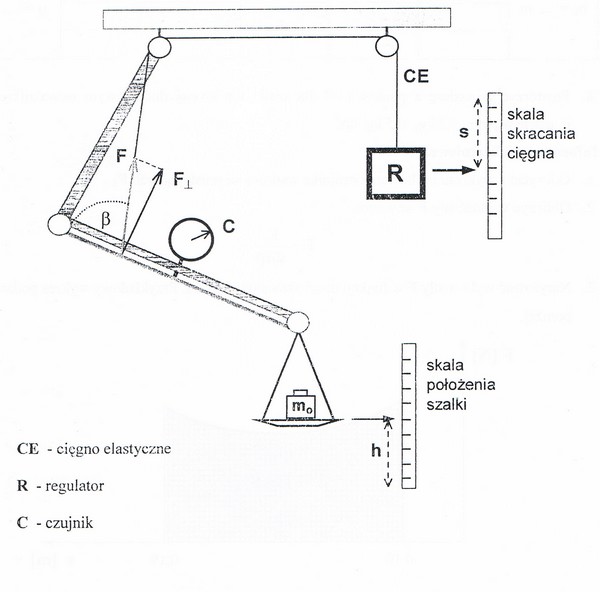
Z doświadczenia takiego możemy odczytać z wykresu cechowania czujnika wartość sił prostopadłych F. Możemy także obliczyć wartość siły F ze wzoru
F=
Wykreślamy również wykres siły F w funkcji drogi skracania cięgna s i wyliczamy pole pod wykresem, które odpowiada wykonanej pracy W. Obliczamy jeszcze energię potencjalną szalki ze wzoru:
Ep=mg(hk-hp)
Gdzie m=ms + mo g=9.81
I na koniec wyznaczamy sprawność układu z zależności:
n=
OGÓLNIE ćwiczenie prowadziło do wyznaczenia pracy oraz sprawności modelu dźwigni szkieletowo - mięśniowych.
WYKRES CECHOWANIA:
54 Właściowości biomechaniczne mięśni
Mięśnie gładkie przy rozciąganiu zachowują się ja model reologiczny Maxwella.
Mięśnie poprzecznie prążkowane zachowują się ta jak ciała lepko-sprężyste(model przedstawiono na ryc.14.60,str.433)
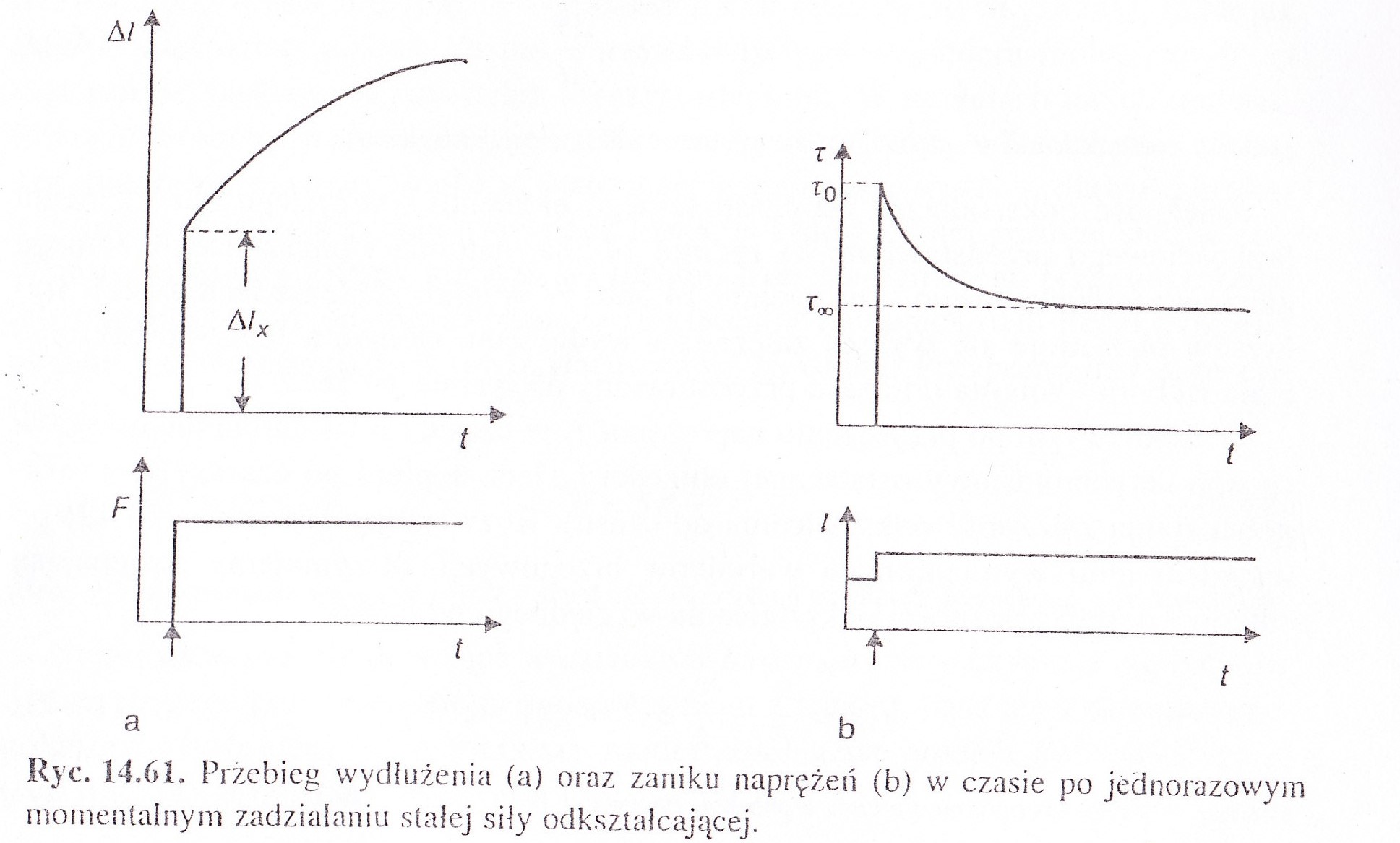
Przebieg wydłużenia w zależności od czasu dla tego modelu na ryc.14.61a.
Przebieg zaniku naprężenia na ryc.14.61b
Naprężenie to znika zgodnie z równaniem:
τ =τ∞ +(τ0-τ∞ )e-t/λ
gdzie, τ∞ -naprężenie graniczne, czyli naprężenie t->∞, λ- czas relaksacji
λ= η/(E1+E2)
Moduł sprężystości w czasie zmienia się według wzoru:
E(t)=E1E2/E1+E2+ (E2-E1E2/E1+E2) e-t/λ
Podobnie zachowuje się model sprężystości mięśni i innych tkanek lepko-sprężystych. Wykazuje on silną zależność od szybkości odkształceń.
Naprężenie w mięśniach p.p:
- mięsień znajdował się w stanie rozciągniętym, następuje jego skrócenie , podczas którego naprężenie szybko spada- nie do 0, do wartości napięcia fizjologicznego mięśnia = naprężenie spoczynkowe(wykres14.62)
Moduł sprężystości rośnie wraz ze wzrostem długości mięśnia( najpierw przy małych zakresach zmian długości nieznacznie, następnie znacznie szybszy). Krzywa naprężeniowo-odkształceniowa składa się z 2 części
A-naprężenie rośnie wolno
B- naprężenie rośnie szybko
Oba te zakresy odkształceń mają odmienne właściwości termodynamiczne( odmienna zależność naprężenia od temp.)
Podgrzewanie mięśnia przy odkształceniach odpowiednio zakresu A i B:
A.
Przy stałej długości mięśnia-wzrost naprężenia
Stałe naprężenie-skrócenie
B.
Przy stałej długości mięśnia-spadek naprężenia
Stałe naprężenie- wydłużenie
Odkształcenia tkanek powodują:
1.zmina energii wewnętrznej
2. zmiana entropii
Na podstawie 1 i 2 zasady termodynamik otrzymujemy: T-temp., U-energia wew., S-entropia, ε- odkształcenie względne.
τ =ρ(U/ε-T S/ε)r
Tak więc mamy źródła wzrostu naprężenia generowanego przez odkształcenie:
-wzrost energii wewnętrznej
- zmniejszenie entropii
Zgodnie z 1 i 2 zasadą termodynamiki: siła którą wydłużamy mięsień F
F=ΔU/Δl-TΔS/Δl
Dla zakresu A:
Zmniejsza się entropia towarzyszy temu wydzielanie ciepła. To zmniejszenie entropii wiąże się z porządkowaniem ogniw makrocząsteczek białkowych odpowiedzialnych za sprężyste właściwości mięśnia w kierunku działania siły-ta część siły sprężystości- termokinetyczna część siły sprężystości.
Dla zakresu B;
Przy dużym rozciągnięciu mięsień pochłania ciepło, następuje wzrost energii wew. Następuje wzrost siły sprężystości( powiększanie się odległości między drobinami białkowymi)
Właściwości elastyczne tkanek są związane z obecnością włókien kolagenu i elastyny. Są one ułożone w ten sposób że przy miernym rozciąganiu tkanki wydłużają się włókna elastylowe, przy większych obciążeniach kolagenowe.
55.Sarkomer, skurcz sarkomeru.
Sarkomer jest podstawową jednostką budowy komórki mięśniowej. Składa się z połówek miofilamentów cienkich - aktynowych (izotropowych) i (całych) miofilamentów grubych - miozynowych (izotropowego). Miofilamenty ograniczone są liniami Z (błonami podstawnymi), które jednocześnie oddzielają sarkomery od siebie. Pod mikroskopem obserwujemy w sarkomerach poprzeczne pasma, od których bierze się nazwa mięśnia poprzecznie prążkowanego szkieletowego.
Do skurczu sarkomeru dochodzi w wyniku zmiany polaryzacji błony komórkowej. Impuls nerwowy, dochodząc do sarkolemy depolaryzuje ją. Poprzez kanaliki T depolaryzacja dociera w okolice miofibryli. Zmiana spadku potencjału powoduje uwalnianie jonów wapniowych, które w fazie spoczynku związane są ze swoistymi białkami (zmiana potencjału wpływa na konformację białka, które zmienia swoje powinowactwo do jonów Ca2+). Jony dyfundują do wnętrza miofibryli i zapoczątkowują skurcz.
Mechanizm skurczu sarkomeru:
Cząsteczki aktyny i miozyny mogą się samorzutnie łączyć ze sobą w kompleks aktynomiozynę. Może on dysocjować na aktynę i miozynę poprzez dodanie ATP, które wiąże się z głową miozyny. Jeżeli dodamy do tego jony Ca2+ to aktywują one ATPazę miozyny i ATP ulega hydrolizie do ADP i Pi, a kompleks aktynomiozynowy ulega odnowieniu (ze względu na brak ATP, który go „blokuje”). Jeżeli ponownie dodamy ATP, znów dojdzie do dysocjacji na aktynę i miozynę. Te właściwości są podstawą skurczu mięśnia.
Wyróżniamy cztery jego fazy. W fazie 1 w głowowej części miozyny znajdują się związane cząsteczki ADP i Pi, a w cytoplazmie komórki nadmiar ATP. W fazie tej mięsień jest w spoczynku. Faza 2, w której głowa miozyny łączy się z aktyną (po aktywacji jonami Ca2+ troponiny C). W fazie 3 z powodu oddziaływania aktyny i miozyny zmienia się konformacja miozyny i głowa odchyla się o kąt 45', następnie zachodzi przesunięcie miofilamentów względem siebie. W fazie 4 cząsteczki ATP wiążą się z miozyną, wypierając cząsteczki ADP i Pi, wiązanie pomiędzy aktyną i miozyną zostaje rozerwane i układ wraca do fazy 1, czyli spoczynku. Przebieg procesu na wszystkich miofilamentach jednocześnie prowadzi do skurczu sarkomeru. W wyniku tego, że wszystkie sarkomery się kurczą, dochodzi do zmniejszenia długości komórki mięśniowej.
56.Miofilament. Skurcz
Aktyna. Cząsteczki aktyny mają kształt kulisty, łatwo polimeryzują, tworząc podwójne helisy. Są one głównym składnikiem miofilamentów cienkich. Oprócz aktyny w ich skład wchodzą cząsteczki tropomiozyny i troponiny. Troponina jest zbudowana z trzech podjednostek: troponiny I, troponiny C i troponiny T.
Miozyna. Cząsteczki miozyny są zbudowane z dwóch głównych łańcuchów polipeptydowych - tzw. łańcuchów ciężkich i czterech dodatkowych - łańcuchów lekkich. Większa część cząsteczki ma budowę podwójnej helisy, lecz głowa (są w niej zlokalizowane łańcuchy lekkie) jest aperiodyczna i to od niej zależy aktywność ATPazy miozyny. Cząsteczki miozyny agregują, tworząc miofilament gruby. Głowy miozyny tworzą wypustki do miofilamentów cienkich. 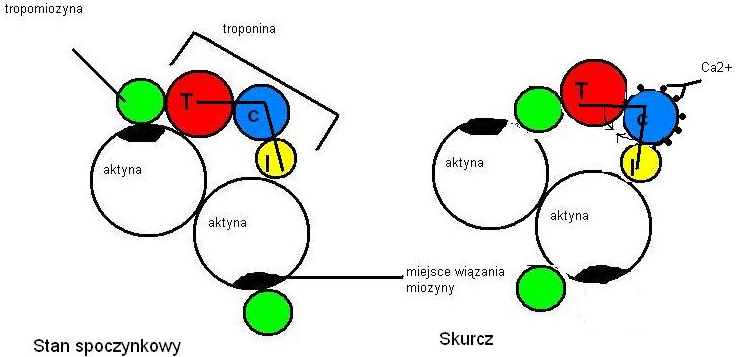
W stanie spoczynku cząsteczki tropomiozyny blokują miejsce wiązania miozyny na aktynie. Podczas skurczu jony Ca2+ łączą się z troponiną C, zmieniając konformację całego kompleksu troponinowego, co pociąga za sobą przesunięcie się tropomiozyny i odsłonięcie miejsc do związania miozyny - może dojść do połączenia miozyny i aktyny, co prowadzi do skurczu.
Pytanie 57 Jaroszyk strona 419 (zielone wydanie) Podstawowe zagadnienia i prawa związane z odkształceniami
Pytanie 58 Rodzaje odkształceń ciał stałych
1) Proste odkształcenie objętości- zostaje wywołane ciśnieniem działającym na ciało równomiernie ze wszystkich stron. Nosi ono nazwę naprężenia normalnego i wyraża się wzorem:
σ = F/Δ S [N/m2 = Pa]
F-wypadkowa sił działających prostopadle na element powierzchniowy ΔS
Miarą odkształcenia objętościowego jest zmiana objętości względnej ΔV/V, wtedy:
σ = K ΔV/V
K- moduł sprężystości objętościowej
2) Proste odkształcenie postaci- zostaje wywołane naprężeniem stycznym , zdefiniowanym zależnością:
τ = F/ ΔS
F-wypadkowa sił działających stycznie do elementu powierzchniowego ΔS
Miarą odkształcenia postaciowego jest kat γ skręcenia prostego, wówczas:
τ = G γ
G- moduł sprężystości postaciowej
59 i 60 Zginanie pręta i skręcanie pręta
Zginanie pręta
Czyste zginanie występuje, gdy siły zewnętrzne działające na belkę po jednej stronie od rozpatrywanego przekroju można sprowadzić do pary sił działających w osi belki lub równolegle do niej. Największe naprężenia występują w strefach skrajnych.
Strzałkę zgięcia S określającą wielkość odkształcenia dla belki w kształcie pręta:
S= 448π ∙ l3Er4 ∙F
r- promień belki
l- długość
Strzałkę zgięcia S, dla belki w kształcie rury zamocowanej na obu końcach i obciążonej w środku siła F, określającą wielkość odkształcenia wyraża wzór:
S= 448π∙ 1E ∙ l3Rz4- Rw4 ∙F
Rz- promień zewnętrzny
Rw- promień wewnętrzny
Ze wzoru wynika że strzałka zgięcia dla rury jest znacznie mniejsza od strzałki dla pręta o tej samej długości i wykonanego z tego samego materiału co rura. Stąd duża wytrzymałość kości przy jednoczesnej oszczędności materiału.
Skręcanie pręta
Skręcanie pręta o długości l zachodzi pod wpływem momentu skręcającego M wywołanego parą sił, przyłożonego w płaszczyźnie prostopadłej do jego osi w jednym końcu, drugi koniec przymocowany.
Kąt skręcenia w mierze łukowej przedstawia wzór:
φrad= 2π ∙ 1G ∙ lR4 ∙M
G- moduł sprężystości poprzecznej
M- moment pary sił
Pytanie 61 i 62
Prawo Hooke'a określa zależność miedzy siłą odkształcającą a odkształceniem dla ciał sprężystych.
τ= F/A = E ∆l/ll0 = E ε
τ- naprężenie
ε- wydłużenie względne
∆l- przyrost długości
l0- długość początkowa
A- pole powierzchni poprzecznego przekroju ciała
F- siła odkształcająca
E- moduł sprężystości podłużnej
Współczynnik Poissona- stosunek względnego wydłużenia poprzecznego εd do względnego wydłużenia podłużnego εp
µ= εd /εp
Pytanie 63 i 64. Energia skurczu mięśnia, wydajność energetyczna. Moc skurczu.
Rozkład ATP i łączenie się miozyny z aktyną są procesami samorzutnymi. Mięsień w fazie rozkurczu jest gotowy do skurczu, ale inhibitor (układ tropomiozyna-troponina) o odpowiedniej konformacji zapobiega skurczowi. Proces rozkurczu wymaga ATP. Ilość ATP w wypoczętym mięśniu wystarcza do kilkuset skurczów. Gdy poziom ATP spada do połowy zdolność do wykonania pracy zanika i mięsień pozostaje w fazie skurczu. Głównym procesem dostarczającym ATP jest oddychanie tlenowe w mitochondriach. W razie niedoboru tlenu zaczyna odgrywać rolę proces glikolizy. Mięsień posiada glikogen, który można rozłożyć do glukozy i z metabolizować. Część ATP mięsień uzyskuje z reakcji fosfokreatyny z ADP.
Miarą energii wyzwolonej w procesach chemicznych jest zmiana entalpii ΔH. Składa się na nią zmiana entalpii swobodnej ΔG oraz zmiana energii związanej TΔS. Procesy zachodzące w mięśniu są nieodwracalne. Entalpia swobodna równa ΔG'=ΔG-ΔQn jest zużyta na pracę, reszta ΔQn=TΔSi wyrażą ciepło nieskompresowane. Mięsień nie pobudzony wykonuje pracę wewnętrzną, która daje ciepło ( ΔWi=ΔGi=ΔG-ΔQni). Te ciepło nazywamy ciepłem spoczynkowym (ΔQsp=ΔHsp=ΔG'i + ΔQni+TΔS). Podczas skurczu izotonicznego, kiedy mięsień skracając się o długość x dźwiga ciężar F, zostaje wykonana praca ΔWe=Fx. Praca ta zostaje wykonana kosztem części zmiany entalpii swobodnej, której towarzyszy jednak wydzielanie dodatkowego ciepła ΔQsk w procesach wzmożonego metabolizmu. Mięsień wykonujący pracę zewnętrzną (ΔHsk=ΔWe+ ΔQsk+ ΔQsp. Na energię skurczu (E) wyraża się praca ΔWe i ciepło skurczu ΔQsk (E=ΔWe + ΔQsk). Na ciepło skurczu składa się ciepło (A)-ciepło aktywacji i ciepło skracania (ax). ΔQsk= A+ax. Ciepło aktywacji wytwarza się po pobudzeniu mięśnia i nie zależy od pracy. Ciepło skracania jest proporcjonalne do długości x skrócenia mięśnia. Współczynnik (a) nie zależy od wielkości naprężenia mięśnia. Po zakończeniu skurczu wydziela się ciepło odnowy.
Wydajność energetyczna η=ΔWe/E . E= A+(F +a)x. Po podstawieniu η=Fx/A+(F+a)x. Z całkowitej energii E można uzyskać moc skurczu. P=dE/dt (iloraz pochodnej energii do pochodnej czasu. Pochodna energii E= (F+a)dx/dt, bo dA=0 (pochodna wartości stałej zawsze jest 0). dx/dt=v (prędkość), więc P=(F+a)v.
65.Zależność siły od skracania mięśnia niepobudzonego
Zależność tą przedstawia ryc. 10.24 na stronie 229 w Pilawskim, można tu wywnioskować, że szybkość skurczu jest największa ,kiedy mięsień kurczy się bez obciążenia, czyli kiedy zwiększamy to obciążenie to szybkość skurczu maleje. Jest to jakby zobrazowanie równania Hilla i stąd wzór na tą szybkość maksymalną skurczu : Vmaks =Fmaks , więc gdy F=Fmaks to V=0.
Jak by spytał o zależność siły odkształcającej mięsień od wydłużenia to wtedy chodzi o zjawisko histerezy- ryc. 10.25 na tej samej stronie
66.Relaksacja- wiąże się z właściwościami lepko- sprężystymi ciał. Wyróżniamy:
Relaksację naprężenia- gdy przyłożymy do ciała naprężenie i spowoduje ono nagłe wydłużenie do pewnej długości ciała, która będzie następnie tak utrzymywana to naprężenie będzie malało z czasem- tą zależność przedstawia ryc. 14.59 b na str. 432 w Jaroszczyku . Relaksacja ta występuje w modelu Maxwella
Relaksację odkształcenia -jeśli utrzymuje stałą siłę, która odkształca ciało to długość ciała rośnie z czasem - jest to zjawisko zwane PŁYNIĘCIEM lub PEŁZANIEM, a zależność wydłużenia ciała w czasie przedstawia wykres 14.58 c na str. 431 w Jaroszczyku. Relaksacja odkształcenia występuje w modelu Kelvina- V oighta
67 i 68
Model Kelvina -Voighta służy do opisu właściwości lepko- sprężystych ciał o przewadze elementów sprężystych. Naprężenie jest sumą naprężeń wywołanych odkształceniem w elemencie sprężystym o module sprężystości E oraz w elemencie lepkim o lepkości η: τ = Eγ + η (dγ/dt)
Po przyłożeniu naprężenia w czasie t=0 ciało to nie osiąga w sposób natychmiastowy ostatecznej długości, lecz dopiero po czasie, po upływie którego odkształcenie= 0,63γo. Czas opóźnienia odkształceń odgrywa ważną role m.in. w układach regulacyjnych.
Model Maxwella służy do opisu właściwości materiałów o przewadze elementów lepkich(ciecze sprężysto- lepkie). Szybkość odkształceń jest sumą szybkości odkształceń zachodzących w elemencie sprężystym oraz lepkim.
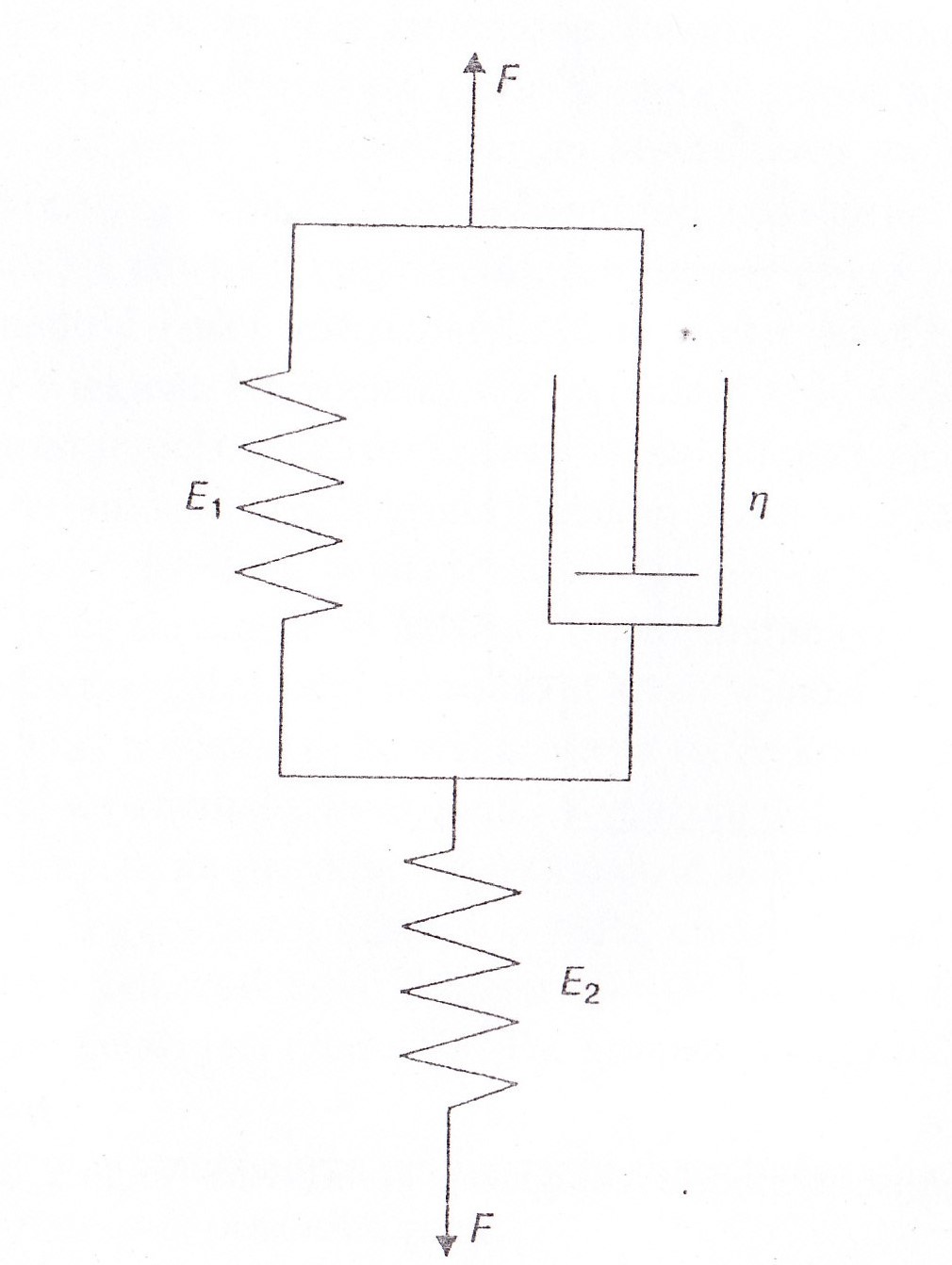
W chwili t=0 naprężenie jest równe naprężeniu max., a następnie zanika do zera w czasie po upływie którego naprężenie spadnie do wartości 0,37 naprężenia początkowego. Czasy relaksacji odgrywają ważną rolę m.in. w zjawisku skracania i wydłużania mięśni, czy w zjawisku odkształcania erytrocytów i leukocytów. Zależności odkształceń-str.431 i 433M
69 model reologiczny mięśnia poprzecznie prążkowanego ( rysunek i wykresy powyzej) Mięśnie poprzecznie prążkowane zachowują się jak ciała lepko-spężyste.
Zanik naprężenia (rys. b) następuje zgodnie ze wzorem:
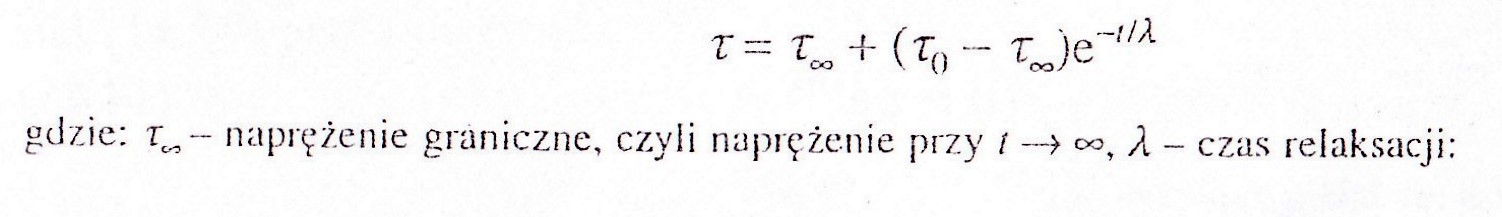
Efektywny moduł sprężystości mięśni
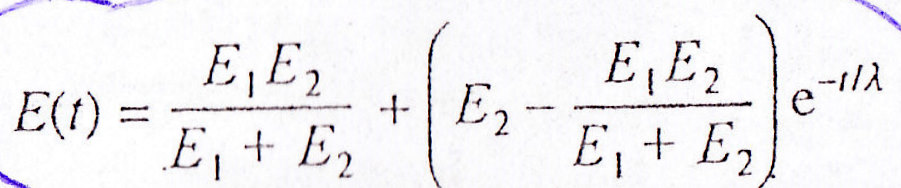
Wykazuje on silną zależność od szybkości odkształceń
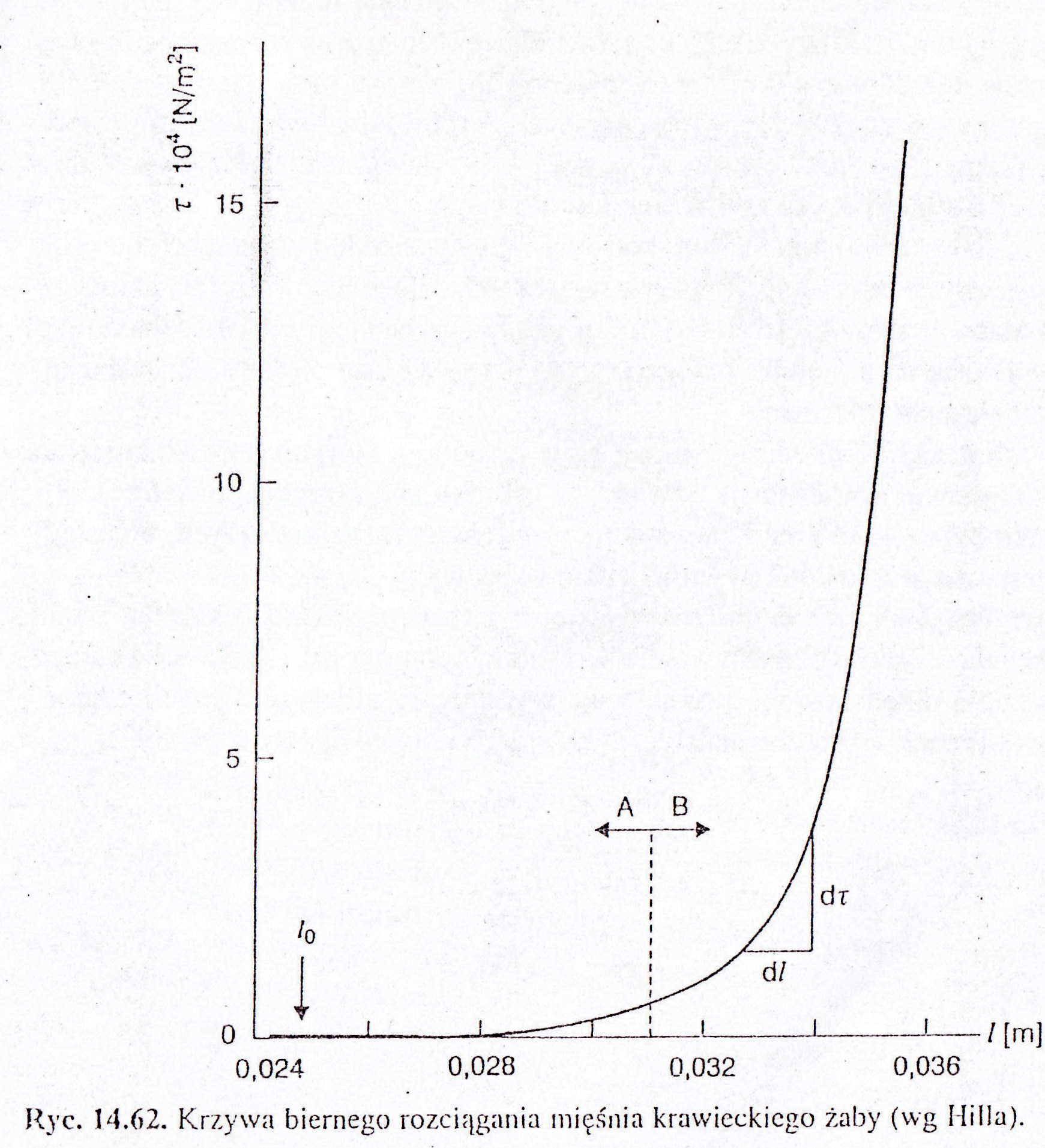
Moduł sprężystości rośnie wraz ze wzrostem długości mięśnia.
W małych zakresach zmian długości wzrost ten jest powolny (A-naprężenie rośnie wolno wraz ze wzrostem odkształcenia).
W dużych zakresach - wzrost jest szybki (B).
Oba zakresy odkształceń charakteryzują się odmiennymi właściwościami termodynamicznymi (mają odmienną zależność naprężenia od temperatury).
W A - gdy stała jest długość mięśnia to podgrzewanie mięśnia powoduje wzrost naprężenia.
gdy stałę jest naprężenie mięśnia to podgrzewanie powoduje jego skrócenie.
W B - zachowanie odwrotne.
72. Prawo Fouriera
Każdy transport wymaga działania bodźców stanowiących „siły napędowe” przepływów. Transport energii (przewodzenie ciepła) opisuje prawo Fouriera:
S - powierzchnia
λ - przewodność cieplna właściwa
dT/dx - spadek temperatur
71.Równanie Hilla
Na ciepło skurczu mięśnia
składa się:
ciepło A - ciepło aktywacji
ciepło skracania q (q=ax) proporcjonalne do długości skrócenia mięśnia
Po zakończeniu skurczu wydziela się tak zwane ciepło odnowy.
Moc P jest proporcjonalna do różnicy między maksymalną siłą F, jaką może wywrzeć mięsień przy skurczu izomerycznym (x=0), a aktualnie przyłożoną siłą.
(F+a)*(v+b)=(Fmaks+a)*b=const
- a,b - współczynniki proporcjonalności
Równanie to nazywamy równaniem Hilla.
Powoduje ono ważną zależność pomiędzy siłą wywieraną przez mięsień a szybkością, z jaką się kurczy. Prędkość skurczu jest największa, gdy miesień kurczy się bez obciążenia. Prędkość maleje wraz ze wzrostem obciążenia i staje się zerem gdy F=Fmaks.
Pytanie 73 - ruch harmoniczny
Ruch harmoniczny zaliczamy do ruchów drgających. Jest to ruch okresowy opisywany sinusoidalna funkcja czasu y=Asin(ωt+ φ)
Gdzie:
y-wychylenie punktu drgającego
omega-czestotliwosc fazowa
phi- stala fazowa
ω=2π/T=2πV częstotliwość zwiazana z okresem drgan
W równaniu ruchu drgającego wychylenie w ruchu harmonicznym zmienia się w czasie sinusoidalnie. Tą zależność przedstawia wykres:
Prędkość w ruchu harmonicznym okresla się wzorem :
V=ωAcos(ωt+φ)
Energia punktu drgającego o masie m jest zawsze rowna sumie Ep+Ek.W chwili odpowiadającej położeniu równowagi Ep=0 wtedy Ek ma wartość maxymalna=całkowitej wartości punktu drgającego:
E=0,5mω2A2
Pytanie 74 Drgania harmoniczne proste
Drgania harmoniczne proste - rzadkie zjawisko-duzo czesciej występują drgania zlozone.
Najprostszy rodzaj drgan okresowych,w których wychylenie ciala zmienia się wedlug wzoru :
A = A0sin(ωt + φ0), gdzie A0 — amplituda, ω — częst. kątowa, t — czas, φ0 — faza początkowa.
75,76
Dowolne złożone drganie okresowe o okresie T można przedstawić w postaci kombinacji liniowej prostych drgań harmonicznych o częstościach kołowych będących wielokrotnościami podstawowej częstości kołowej
:
.
Taki sposób przedstawienia funkcji okresowej nazywamy rozwinięciem tej funkcji w szereg Fouriera, lub analizą Fourierowską. Każdy wyraz szeregu odpowiada jednemu składowemu drganiu harmonicznemu o częstości kołowej w, 2w, 3w itd. Zbiór wszystkich czsto[ci skBadowych tworzy tzw. widmo rozważanej funkcji f(t). Skład widma zależy od postaci funkcji f(t). Drgania okresowe mają zawsze liniowe (dyskretne) widmo częstości. W prostych przypadkach widmo może składać się z niewielkiej liczby częstości. Istnieje również możliwość przeprowadzenia analizy Fourierowskiej funkcji nieokresowych (np. zmierzonych sygnałów). Zwykle jednak drgania nieokresowe mają ciągłe widmo częstości, oznacza to, że można je przedstawić w postaci złożenia olbrzymiej liczby drgań harmonicznych
Ryc.11.3 str. 239 Pilawski
Pytanie 77 - Drgania tłumione
Występują gdy na ruch drgający działa siła hamująca powodująca wykładniczy spadek amplitudy w czasie, zgodnie z równaniem:
A - amplituda - amplituda początkowa δ - współczynnik tłumienia, t - czas
δ wyraża liczbę drgań po których A zmniejszy się e-krotnie (czyli 2,72 razy)
to czas relaksacji, czyli czas, po którym A zmniejszy się do 37% wartości
Wykres zależności względnego spadku amplitudy od czasu znajdziecie na stronie 240 w pilawskim w materiałach z ćw. 2 - ryc. 11.4 (sorry ale nie mam skanera )
Pytanie 78 - związek między okresem drgań i siłą tłumienia
Okres drgań układu tłumionego (czy takiego, na który działa stała siła hamująca zmniejszająca amplitudę) wyraża się wzorem:
- dgrania własne układu δ - współczynnik tłumienia
Przy dużym tłumieniu, gdy > drgania stają się aperiodyczne (wartość pod pierwiastkiem staje się ujemna co nie ma sensu fizycznego, więc wtedy nie istnieje).
Jeżeli na ruch drgający działa siła zmienna, o jakiejś częstości kołowej to wtedy układ też zaczyna drgać z tą częstotliwością (czyli jakby podporządkowuje się tej zewnętrznej sile)wykonując tzw. drgania wymuszone. Im mniejsza jest różnica między częstotliwością drgań własnych i drgań „narzuconych” tym większa jest amplituda drgań wymuszonych, która osiąga maksimum gdy wystąpi rezonans, czyli
Ogólnie: im większe tłumienie tym mniejsza amplituda.
Wykres ryc.11.5 znajduje się w pilawskim na stronie 240
79.WPŁYW PRZECIĄŻEŃ NA ORGANIZM
Człowiek nie odczuwa negatywnych skutków przemieszczania się nawet z bardzo dużymi prędkościami - problemy pojawiają się przy zmianie prędkości, a więc wtedy gdy istnieje przyspieszenie.
Przyczyny pojawienia się przyspieszeń to zmiany:
Wartości prędkości liniowej w ruchu prostoliniowym
Kierunku prędkości w ruchu krzywoliniowym
Wartości prędkości kątowej
Wartość przyspieszenia liniowego wyrażamy jako n wielokrotności przyspieszenia ziemskiego (g) a=ng
Wpływ przyspieszenia zależy od:
Wartości przyspieszenia i szybkości jego zmian
Czasu trwania
Kierunku i zwrotu
Kondycji organizmu
Przyspieszenia (ze względu na czas trwania):
Udarowe t 0,05s
Krótkotrwałe 0,5s < t < 1s
Przedłużone 1s < t < kilka s
Przewlekłe t > kilka s
Przyspieszenia:
wzdłuż podłużnej osi ciała:
+Gz (głowa -> stopy)
-Gz (stopy -> głowa)
w strzałkowej osi ciała:
+Gx (mostek -> plecy)
-Gx (plecy -> mostek)
w poprzecznej osi ciała:
+Gy (prawa -> lewa)
-Gy (lewa - > prawa)
Wpływ przyspieszeń podłużnych (Gz)
Pozornie zwiększenie masy ciała
Tkanki i narządy opadają w dół -> zmiana ciśnienia w jamie brzusznej; przesunięcie przepony w dół powoduje zwiększa pojemność życiową płuc, a ograniczenie jej ruchów spłyca oddechy)
Spadek ciśnienia krwi ( 30mm Hg na każde 1g) w górnych obszarach ciała, wzrost ciśnienia i zastój krwi w kończynach dolnych
Podtrzymanie krążenia w mózgu wymaga zwiększonej pracy serca [niedotlenienie OUN to utrata widzenia obwodowego (3,5 -4g przez 5s), widzenia centralnego (4,5 -5,5g), utrata świadomości (5,5 - 6,5g przez 10s)]
„push-pull” - tolerancja na przeciążenia +Gz jest obniżona po wcześniejszym zadziałaniu przyspieszenia -Gz
bardziej szkodliwe
przemieszczenie krwi do mózgu: ból głowy (2-3g), przyrost ciśnienia o 70-90mm Hg (3g). Zaburzenia krążenia mózgowego to wydłużenie czasu krążenia i spadek ciśnienia tętnyczo-żylnego. Znaczne zmiany rytmu serca i zmiany w OUN
przy silnych przyspieszeniach udarowych (króciutkich) dochodzi do wylewów do mózgu
przemieszczenie narządów w jamie brzusznej ku górze zmniejsza pojemność oddechową płuc i częstotliwość oddechów (już przy 2,5g)
Wpływ przyspieszeń poprzecznych (Gy) i strzałowych (Gx)
Skutki obu są do siebie podobne
Kompresja klatki piersiowej i jamy brzusznej oraz przesunięcie i spłaszczenie przepony. Zmniejsza się pojemność płuc, oddychanie jest utrudnione (nasycenie krwi tlenem spada przy 6g o 13%, a przy 8g o 23%)
Zakłócenie pracy serca (6g zwalnia ją o 14%)
Siła ciężkości (g) wpływa na ciśnienie w naczyniach krwionośnych przez istnienie ciśnienia hydrostatycznego (zależnego od wysokości h)
W pozycji pionowej, gdy na poziomie serca ciśnienie w aorcie wynosi 13kPa (100mm Hg) to w dużej tętnicy głowy (h = 0,5m nad poziomem serca) ciśnienie jest o 5kPa mniejsze, a w dużej tętnicy stopy (h = 1m poniżej poziomu serca) ciśnienie jest o 10kPa większe. Nadwyżka ta jest zrównoważona ciśnieniem hydrostatycznym układu żylnego na zasadzie naczyń połączonych.
W pozycji poziomej ciśnienie hydrostatyczne nie ma większego znaczenia
Znaczne różnice ciśnień w naczyniach mogą wystąpić przy przeciążeniach przyspieszeniowych (patrz pytanie 79.)
OKULISTYKA- przyspawanie odwarstwionej siatkówki, tamowanie krwotoków wewnątrz gałki ocznej, leczenie jaskry i zaćmy.
Aktualnie próbuje się stosować je w onkologii - likwidacja mikroskopijnych ognisk nowotworowych.
Stomatologia - usuwanie próchnicy, plomby
Mikrochirurgia
Holografia - na mój gust to sobie można odpuścić…
Gdy promień w przestrzeni przedmiotowej jest równoległy do osi (punkt A jest odsunięty nieskończenie daleko, s=∞)
Gdy promień załamany jest równoległy do osi, obraz A' jest w nieskończoności, s'=∞
zdolnośc skupiająca D- odwrotnośc ogniskowej obrazowej, mierzymy ją w dioptriach (1 dptr=1/m) D=1/f'
Układ o zdolności skupiającej dodatniej skupia dodatnie, układ o zdolności skupiającej ujemnej skupia ujemnie (czyli rozprasza).
Dwa układy optyczne o zdolnościach skupiających równych co do wartości i różnych co do znaku mają wynikową zdolność skupiającą zawsze dodatnią
Im większa jest zdolność skupiająca soczewki korekcyjnej, tym bardziej „czuła” jest korekcja na zmiany odległości
Zdolności rozdzielczej jego układu optycznego
Czułości receptora (elementu światłoczułego oka) - jaka zmiana natężeń światła może być zarejestrowana
Wielkość powierzchni receptora
Jeżeli zarejestrowane zostaną przez jeden element światłoczuły, to zostaną one odebrane jako jeden punkt.
Jeżeli zostaną zarejestrowane przez rożne elementy światłoczułe i owe elementy sąsiadują ze sobą to nadal nie wiadomo czy to dwa punkty czy jeden taka „ziarnista” struktura fotoczuła rozróżnia dwa punkty wtedy, gdy pobudzone receptory elementarne rozdzielone są przynajmniej jednym niepobudzonym (a osie obrazów dwóch punktów przenikają siatkówkę w odległości 4 m od siebie - wtedy kąt jest równy 0,25 x 10 -3 rad).
średnica źrenicy - regulacja dopływu światła
ośrodki przezierne oka (np. rogówka, ciecz wodnista, ciało szkliste) - absorbcja 50% światła widzialnego i całkowita absorbcja UV
widzenie za pomocą pary oczu jest mechanizmem pozwalającym na dokładną ocenę trójwymiarowości obrazu.
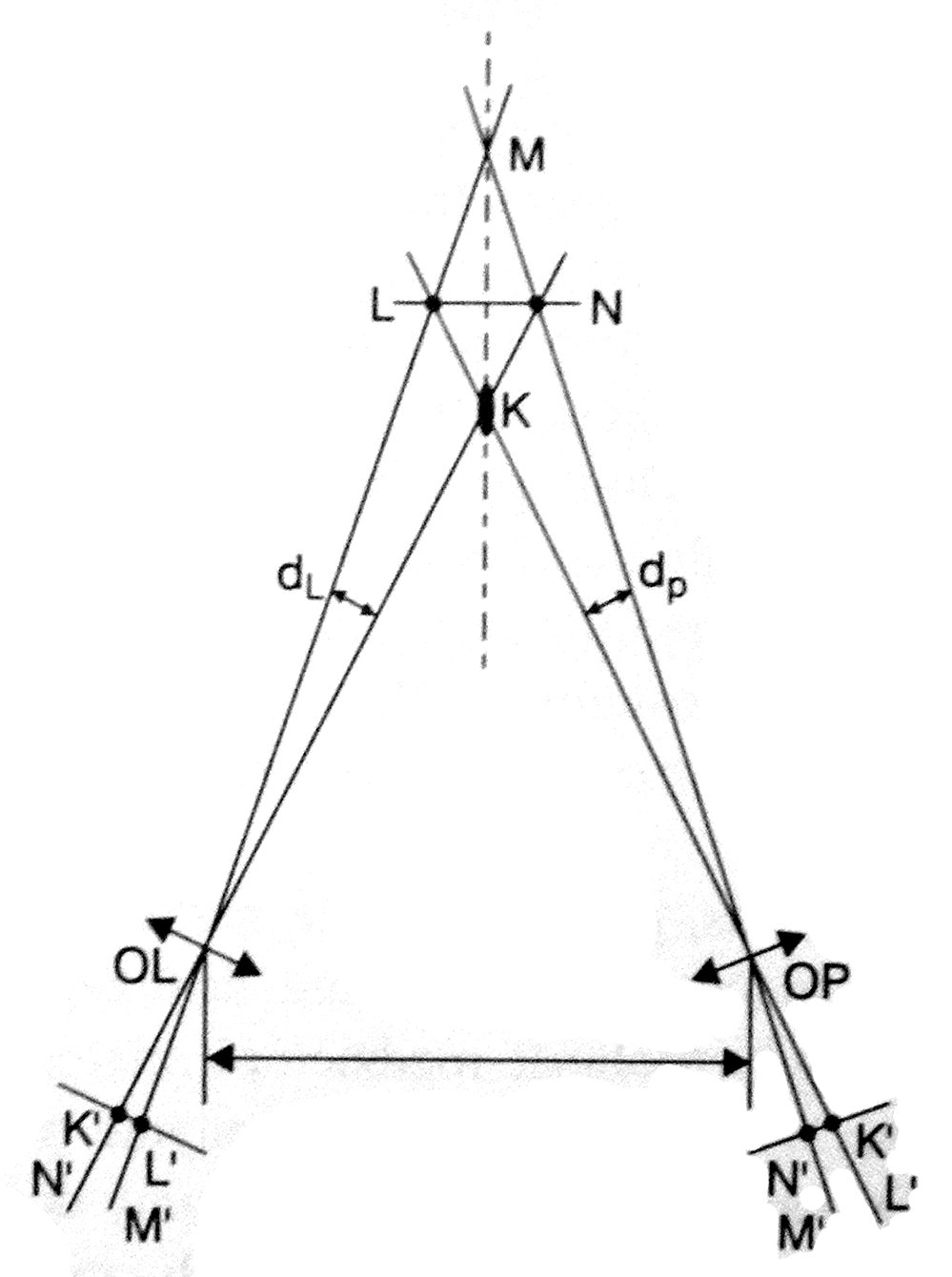
gdy dwa przedmioty (L i N) są jednakowo odległe od obserwatora, ich obrazy (N' i L') powstają na obu siatkówkach w tej samej kolejności - N' i L', od lewej do prawej.gdy dwa przedmioty (M i K) są w różnej odległości od obserwatora, ich obrazy (M' i K') powstają symetrycznie (M' przyśrodkowo, K' bocznie).
jeżeli przesuwamy obiekt bez zmiany odległości (poziomo, na naszym rysunku), to jego obraz na obydwu siatkówkach będzie się przesuwał w tym samym kierunku (w lewo albo w prawo).
jeżeli przesuwamy obiekt ze zmianą odległości, obraz na obu siatkówkach będzie przesuwał się w przeciwnych kierunkach (tzn. oba obrazy będą dążyły „do nosa” albo „do skroni”)
Miarą widzenia przestrzennego jest bezwzględna różnica kątów, pod jakimi każde z oczu widzi dwa przedmioty, jeszcze rozpoznawane jako położone w różnej odległości. Na rysunku górnym, przy założeniu, że |KM| to właśnie ta minimalna odległość, wzór wygląda:
Dobrą ilustracją dla zrozumienia, o co w tym chodzi, jest rysunek obok, gdzie obiekty ustawiono tak, że kąt dla jednego z oczu wynosi 0 (θ jest tu równoznaczne z γ).
γ jest bardzo małą wielkością - średnio rzędu 10'-12'.
Zdolność rozdzielczą można zwiększyć stosując immersję (czyli zwiększamy współczynnik załamania n)
Zdolność rozdzielczą można zwiększyć stosując światło o któtszej fali (czyli zmniejszamy λ)
apertura numeryczna obiektywu
stała
dla zwiększenia zdolności rozdzielczej mikroskopu można stosować imersję (n>1)
można również zastosować światło o krótszej fali dla tego samego efektu
Płuca znajdują się w klatce piersiowej , szczelnie zamkniętej przestrzeni w której panuje ciśnienie zwane ciśnieniem wewnątrzopłucnowym pop
Ciśnienie powietrza w płucach (w pęcherzykach płucnych) nazywane jest ciśnieniem śródpęcherzykowym pp
Pęcherzyki płucne oplecione są sprężystymi włókienkami białkowymi m. in. kolagenowymi które nadają tkance płucnej pewne właściwości sprężyste. Siły sprężystości usiłują zmniejszyć objętość płuc i w efekcie przy otwartej klatce piersiowej obserwujemy ich zapadanie. W zamkniętej klatce piersiowej płuca wypełniają ją całkowicie - co jest związane z różnicą ciśnień między płucami a przestrzenią opłucnową -> pp > pop . Różnica ciśnień rozciąga płuca, działając tym samym przeciw naprężeniom sprężystym tkanki płucnej.
Wynikiem działania sił sprężystych tkanki płucnej jest ciśnienie sprężyste tkanki płucnej - psp , które w stanie równowagi jest równe różnicy ciśnień śródpęcherzykowego i wewnatrzopłucnowego.
W stanie spoczynku ciśnienie śródpęcherzykowe jest równe ciśnieniu atmosferycznemu, które przyjmuje wartość = 0. W związku z tym ciśnienie wewnątrzopłucnowe , które musi byś mniejsze od śródpęcherzykowego - jest ujemne.
Podczas wdechu zostaje do płuc wprowadzona objętość zwana objętością oddechową
Objętość powietrza wdychana i wydychana w ciągu minuty - to wentylacja minutowa i przy spokojnym oddychaniu wyn. ok. 8dm3/min.
objętość nie wzrasta - jest wiele zapadniętych pęcherzyków, szczególnie małych (siły adhezji) i aby je otworzyć potrzeba tzw. ciśnienia otwarcia
objętość rośnie ze wzrostem ciśnienia
najpierw nieznacznie - wypełniają się na początku większe, mniej odporne pęcherzyki
następnie coraz gwałtowniej - napełniają się małe pęcherzyki co prowadzi do znacznego wzrostu objętościobjętość przestaje wzrastać - zaczynają działać siły sprężystości ograniczając przyrost objętości (jednocześnie zapobiega to pęknięciu pęcherzyka)
gwałtowny spadek ciśnienia przy nieznacznej zmianie objętości - gwałtownie maleją siły sprężyste
objętość maleje wraz z ciśnieniem (nie powoduje to zapadnięcia się płuc dzięki napięciom powierzchniowym)
Mała pętla na wykresie odpowiada procesowi spokojnego oddychania
wydajność z jaką organizm przekształca energię chemiczną na pracę mechaniczną (wartość w granicach 20-25%, gdyż jest to stosunek wykonanej pracy wewnętznej We do zużytej na ten cel energi ΔHe a nie do całej pobranej energi)
przemianę podstawową materii - najmniejszą moc energii jaką organizm potrzebuje do utrzymania procesów życiowych będąc w całkowitym spoczynku. Przemiana ta wynosi średnio 80W = 1700 kcal/24h
reakcja jest egzotermiczna jeżeli ΔU<0 albo ΔH<0 czyli gdy układ oddaje energię do otoczenia.
reakcja jest endotermiczna jeżeli ΔU>0 albo ΔH>0 czyli gdy układ pobiera energią z otoczenia.
do opisu kinetyki procesu służy pojęci szybkości zmiany entropii dS/dt;
na szybkość zmieniania się entropii układu składa się:
216. Ogniwo stężeniowe
Dokuczliwy we wnętrzach 35-40 dB (średnio głośna rozmowa)
Krytyczny 85-90 dB (np. syrena alarmowa)
Systematyczne
Spowodowane niewłaściwym wyskalowaniem przyrządów pomiarowych, opóźnionym refleksem osoby wykonującej pomiar, niewłaściwym ustawieniem „zera” na przyrządzie pomiarowym.
Są proste do wyeliminowania przez odpowiednią kalibrację przyrządów pomiarowych.Przypadkowe
Spowodowane chwilową niedyspozycją lub dekoncentracją osoby wykonującej pomiar, zmianami warunków podczas wykonywania pomiarów (skoki napięcia, wahania wilgotności, temperatury, zbyt głośne lub ciche otoczenie).
Nie da się ich wyeliminować.Grube
Spowodowane przez niewłaściwy zapis jednostek mierzonej wielkości, niewłaściwy odczyt wielkości mierzonej.
Są łatwe do wyeliminowania, ponieważ znacznie odbiegają od wartości normalnych. Pomiary z błędem grubym powinno się wykreślać i na ich miejsce wykonywać nowy pomiar.Bezwzględne Δxi=xi-xrzeczywiste
jest to wartość inna dla każdego pomiaru, zależy od jednostkiWzględne δ=Δxi/xrzeczywiste (*100%)
nie zależy od jednostek, jest to wielkość bezwymiarowa lub w %ABSORPCJA-wynik zamiany energii mechanicznej drgań cząstek ośrodka na ciepło
ROZPRASZANIE- związane z niejednorodnością ośrodków w których ultradźwięki się rozchodzą
Prędkość ultradźwięków w tkankach zależy od dwóch wartości:
ρ- gęstość ośrodka
Tłumienie
Odbicie
stałym polem magnetycznym \vec B_z, które jest wytwarzane magnesami (oś "Z" jest osią magnesu spektrometru, w literaturze często zamiast \vec B_z pisze się \vec B_0 ),
zmiennym polem magnetycznym \vec B_{xy}(t), skierowanym prostopadle do osi "Z" (generowanym przez fale elektromagnetyczne w cewce spektrometru, w literaturze \vec B_{xy} określane jest jako \vec B_1),
zmiennymi polami lokalnymi generowanymi przez sąsiednie jądra atomów oraz znajdujące się na nich chmury elektronowe.
Mechanizm działania:
przy +Gz
przy -Gz
80. WPŁYW SIŁY CIĘŻKOŚCI NA KRĄŻENIE
p= ρgh
ρ- gęstość cieczy
81. Wpływ temperatury na szybkość procesów biologicznych
Temperatura wpływa na:
- współczynnik dyfuzji, lepkości
- ciśnienie
- pot. Elektrochemiczne, pot. Chemiczne (szybkość reakcji chemicznej)
- trwałość zw. biochem.
- procesy metabolizmu, transportu
- pot. Bioelektryczne zw. pobudliwością komórek
Szybkość procesów biologicznych związana jest przede wszystkim z szybkością przebiegu reakcji chemicznych. Zależność szybkości reakcji chemicznych od temperatury wyraża prawo Arrheniusa, według którego stała szybkość reakcji
Procesy biologiczne zachodzą w przybliżeniu zgodnie z tym prawem. Wartość energii aktywacji Ea daje przy tym pewien pogląd na mechanizmy przebiegu procesu. Jednak wyznaczanie energii aktywacji dla procesów biologicznych jest często kłopotliwe, jeżeli w ogóle możliwe. Dlatego dla wyrażenia wpływu temperatury na procesy biologiczne wprowadza się współczynnik Van't Hoffa zwany współczynnikiem Q10. Współczynnik Q10 definiuje się stosunkiem szybkości przebiegu procesu w temperaturze (T + 10K) do jego szybkości w temperaturze T, czyli
Dla procesów zachodzących w organizmach żywych wartość Q10 jest zawarta w przybliżeniu w granicach 1÷4.
Dla procesów o charakterze fizycznym, np. dyfuzji w przybliżeniu jest 1,03< Q10<1,3.
Dla procesów o charakterze chemicznym jest na ogół 2 < Q10 < 3, dla enzymatycznych Q10 < 2.
Temperatura ma szczególnie duży wpływ na szybkość przewodzenia stanu pobudzenia. Istnieje pewna temperatura optymalna, dla stałocieplnych nieco ponad 40◦C w której szybkość przewodzenia jest największa.
Pyt. 82 Rola wilgoci w regulacji cieplnej ustroju, wzór i interpretacja.
Zmiana wilgotności otoczenia będzie miała decydujący wpływ na udział mechanizmu parowania w stratach cieplnych organizmów żywych. Równanie określające gęstość strumienia CIEPŁA PAROWANIA- :
Można również przedstawić w postaci:
Gdzie: stosunek ciśnienia cząstkowego pary wodnej w otoczeniu do ciśnienia cząstkowego pary wodnej na powierzchni skóry żywego człowieka. W przybliżeniu:
wilgotność względna powietrza ciśnienie cząstkowe pary wodnej nasyconej w temperaturze pary wodnej znajdującej się w otoczeniu i mającej ciśnienie cząstkowe
Przy wilgotności względnej procesy parowania z powierzchni skóry są zatrzymane.
Przy temperaturach powietrza niższych niż 30 ̊Cnie stwierdza się istotnego wpływu wilgoci względnej na temperaturę skóry żywego organizmu. Wilgotność wpływa na tzw. KOMFORT KLIMATOLOGICZNY żywego organizmu. Optymalny komfort- gdy wilgotność względna jest zawarta w granicach 40-75℅, a zakres temperatur otoczenia wynosi 25-35 ̊C.
Gdy temperaturach skóry niższych od temperatury otoczenia i wysokich wilgotnościach względnych parowanie staje się niemożliwe- organizm człowieka nie toleruje takiej sytuacji.
W wysokich temperaturach ale w całkowicie suchym powietrzu, w warunkach przemiany spoczynkowej , temperatura T organizmu nie ulegnie zmianie- do 15 min.
Na warunki wymiany ciepła oprócz temperatury otoczenia i jego wilgotności ma również prędkość ruchu powietrza. Zwiększenie ruchu powietrza powoduje wzrost strat cieplnych przez konwekcję i parowanie, a ich zmniejszenie przez mechanizm promieniowania.
83. Sposoby transportu ciepła.
86. Przewodnictwo
87. Konwekcja
Średnią temperaturę ciała, w normalnych warunkach otoczenia, oblicza się wzorem przybliżonym
Gdzie:
Ts - temperatura skóry
Tr - temperatura mierzona w odbycie
Wymiana ciepła pomiędzy organizmem a otoczeniem odbywa się przez:
1 przewodzenie ciepła
2 konwekcję
3 promieniowanie
4 parowanie wody
Na strumień ciepła oddany do otoczenia składają się :
-strumień zawiązany z konwekcją
-strumień związany z promieniowaniem
- strumień związany z parowaniem
1.PRZEWODZENIE- ma miejsce tylko przy przechodzeniu ciepła przez zewnętrzną powłokę ciała, przez warstwę powietrza przylegającą bezpośrednio do skóry. Np. przy siedzeniu.
2.KONWEKCJA- zjawisko unoszenia ciepła za pośrednictwem poruszającej się substancji. Powietrze ogrzewa i unosi się jego miejsce zajmuje powietrze chłodniejsze.
- współczynnik ostygania zal od ruchu otaczającego powietrza, gęstości, lepkości, od kształtu powierzchni oddającej ciepło, przy wietrze ten współczynnik jest większy
3. PROMIENIOWANIE -przy temperaturach ciała wyższych od otoczenia, energia jest przekazywana do otoczenia za pośrednictwem promieniowania elektromagnetycznego w zakresie podczerwieni
Strumień ciepła oddanego do otoczenia wyraża wzór Stefana-Boltzmana:
-temp skóry
-temp przedmiotów otaczających
-stała promieniowania ciała doskonale czarnego
-zdolność absorpcyjna powierzchni promieniującej
4. PAROWANIE - gdy temp otoczenia zbliży się do temp skóry zawodzą mechanizmy utraty ciepła przez konwekcję i promieniowanie, pozostaje więc parowanie. Woda stale wydzielana przez skórę wyparowując pobiera ciepło parowania. Przy zbyt obfitym wydzielaniu potu, szybkość parowania może być niewystarczająca, wtedy nadmiar potu opada kroplami. Jest to niekorzystne bo woda nie wyparowując nie pobiera ciepła parowania.
pS i pp - odpowiednio ciśnienia cząstkowe pary wodnej przy powierzchni skóry i w otaczającym powietrzu,
Sp -powierzchnia biorąca udział w parowaniu. Współczynnik kp zależy między innymi od ciepła parowania wody, ruchu powietrza itd.
NAJWIĘCEJ CIEPŁA ODDAWANE PRZEZ WYPROMIENIOWANIE
84.Granice tolerancji zmian temperatury.
Człowiek może trwać w stanie homeostazy tylko w określonych warunkach środowiska. Zbyt wysoka temperatura otoczenia wprowadza ustrój w stan hipertermii. Wtedy ciepło oddawane do otoczenia nie jest w stanie zbilansować ciepła wytwarzanego w organizmie i jego temperatura wewnętrzna rośnie. Przy zbyt niskiej temperaturze otoczenia - stan hipotermii, gdy ciepło oddawane do otoczenia przeważa nad ciepłem wytwarzanym, temperatura wewnętrzna się zmniejsza. Odchylenia temperatury ( w normie około 37 stopni C) o około 2 ͦC są przez organizm tolerowane. Wzrost temperatury wewnętrznej do 41:42 stopnie C wprowadza zakłócenia w funkcjonowaniu ośrodka centralnego, co prowadzi do wyłączenia termoregulacji. Wzrost temperatury powoduje wtedy wzmożenie procesów metabolicznych (zgodnie z prawem Arrheniusa )co pociąga za sobą wzrost wytwarzania ciepła. Sprzężenie zwrotne staje się dodatnie - układ zamiast działać w kierunku zmniejszenia skutków zakłócenia - przeciwnie, skutki te wzmacnia. Przy temperaturze wewnętrznej 44:45 stopni C zachodzą w organizmie zmiany nieodwracalne kończące się śmiercią osobnika. Obniżenie temperatury wewnętrzne poniżej 33 stopni C wprowadza zaburzenia w sprawnym działaniu termoregulacji a przy 30 stopniach C całkowite jej wyłączenie. Przy 28 stopniach C pojawia się zagrażające życiu zakłócenie rytmu serca.
Organizm jest bardziej odporny na hipo- niż na hipertermię. Pod ścisłym nadzorem, na krótki okres temperatura wewnętrzna może być obniżona nawet do 24 ͦC.
Pyt. 85. Rozkład temperatury w organizmie człowieka.
W przybliżeniu stałą temp. Utrzymuje tylko wnętrze organizmu. Powłoka zewnętrzna zmienia temp. Zależnie od warunków otoczenia. Grubość tej powłoki- dochodzi do 2,5 cm - co stanowi 20-30%. Ciepło wytworzone w narządach o dużym metabolizmie jest rozprowadzana przez krew po całym organizmie. Przez KONWEKCJĘ dostaje się także do powłoki powierzchniowej. Przy niższych temp. otoczenia, zewnętrzna powierzchnia ciała ma temp. niższą od jej wnętrza . W powłoce powierzchniowej istnieje wtedy spadek temperatury warunkujący transport ciepła przez przewodnictwo cieplne. Ten transport uzależniony jest od przewodności właściwej warstw powierzchniowych i od spadku temperatury gdzie Δx- grubosć warstwy przewodzącej ciepło) oraz od powierzchni S, przez którą ciepło jest przewodzone.
Przewodność właściwa λ tkanki uzależniona jest od stopnia ukrwienia, co wiąże się ze stanem rozszerzenia naczyń krwionośnych. Od tego stanu zależy też grubość warstwy powierzchniowej, a wiec i spadek temperatury. Transport ciepła poprzez powlokę wiąże się z NACZYNIORUCHOWOŚCIĄ.
88 - PRAWO ARRHENIUSA, WZÓR, INTERPRETACJA:
Szybkość procesów biologicznych związana jest przede wszystkim z szybkością przebiegu reakcji chemicznych.
PRAWO ARRHENIUSA - wyraża ono zależność szybkości reakcji chemicznej od temperatury. Według niego stała szybkości reakcji (k) wynosi:
Ea - energia aktywacji
A - stała dla danej reakcji
R - stała gazowa
T - temperatura
Pyt. 89 Współczynnik Q. Rola.
Współczynnik Q- wyraża wpływ temperatury na procesy biologiczne.
Współczynnik Q10- Stosunek szybkości przebiegu procesu w temperaturze (T+ 10K) do jego szybkości w temperaturze T:
Zgodnie z prawem Arrheniusa:
Albo:
Dla procesów zachodzących w organizmach żywych wartość Q jest zawarta w przybliżeniu w granicach 1-4. Dla procesów o charakterze fizycznym np. dyfuzji, potencjałów błonowych od 1,03- 1,3. Dla procesów o charakterze chemicznym 2-3, dla enzymatycznych mniejsze niż 2.
zachowuje się w szczególny sposób w okresie pobudzenia komórki. W okresie narastania potencjału czynnościowego Q zawarte jest w granicach 1,7-2, natomiast w okresie powrotu do stanu spoczynkowego ( w okresie refrakcji) zawiera się w granicach 2-4. Można wnioskować że procesy wywołujące pobudzenie są zbliżone do procesów typu fizycznego, natomiast podczas powrotu do stanu spoczynkowego- do chemicznego.
Pyt. 90. Fala tętna. Szybkość.
Fala tętna- Fala odkształceń sprężystych wywołana rytmicznymi skurczami serca, przenosząca się ruchem falowym wzdłuż tętnic, aż zostanie stłumiona w łożysku małych naczyń.
Szybkość fali tętna wyraża wzór:
c= gdzie: E- moduł Younga ścian naczynia, e- grubość ściany, ρ- gęstość, r- promień przekroju
Wzór Moensa- lepiej zgadza się z wynikami doświadczalnymi:
gdzie F oznacza współczynnik empiryczny- dlaaory człowieka przy ciśnieniu rozkurczowym (,5 kPa wynosi 0,6-0,7.
Pyt. 91. Impedancja tętnicza. Definicja, wzór, rola.
Średnia energia kinetyczna Ek porcji krwi o masie m wyraża się wzorem:
gdzie v- średnia prędkość liniowa porcji krwi o masie m=ρΔxS, gdzie ρ- gęstość krwi, Δx- droga którą przebywa fala tetna o prędkości w czasie, S- powierzchnia pola poprzecznego przekroju naczynia. Zatem:
Natomiast prędkość liniową krwi v można wyrazić jako stosunek strumienia objętości porcji krwi Q do powierzchni pola poprzecznego S: Zatem maksymalna energia kinetyczna wynosi:
Energia ta zamienia się na energię potencjalną sprężystości :
Gdzie: odpowiednio ciśnienie skurczowe i rozkurczowe, ΔV- objętość porcji krwi.
Porównując i - Zasada zachowania energii oraz dzieląc obustronnie przez Δt po uporządkowaniu otrzymujemy:
Lewa strona równania- DEFINICJA IMPEDANCJI TETNICZEJ
Prawa strona- określa czynniki, które wpływają na impedancję tętniczą- gęstość krwi, prędkość fali tętna, pole poprzecznego przekroju tętnicy. Impedancja tętnicza w obwodzie tętniczym naczyń krwionośnych odgrywa analogiczną rolę jak impedancja elektryczna w obwodzie RLC.
Pyt.92. Opór naczyniowy - współczynnik, wzór, rola, wartość.
Współczynnik R nosi nazwę OPORU NACZYNIOWEGO PRZEPŁYWU.
Można stwierdzić , że opór naczyniowy jest odwrotnie proporcjonalny do kwadratu pola przekroju przewodu . Gdy układ składa się z przewodników o różnym przekroju, różnym odcinkom układu odpowiada różny opór a więc i różny spadek ciśnienia. Na przewodzie o większym przekroju (mniejszym oporze) spadek ciśnienia jest mniejszy.
93 - PORÓWNANIE OPORU NACZYNIOWEGO Z ELEKTRYCZNYM:
R = Δ p/Q -> opór naczyniowy przepływu
analogia do prawa Ohma:
Opór odcinka przewodnika o stałym przekroju poprzecznym jest proporcjonalny do długości tego odcinka i odwrotnie proporcjonalny do pola powierzchni przekroju
Opór naczyniowy jest odwrotnie proporcjonalny do kwadratu pola przekroju przewodu ( л r^2)^2 ,
inaczej jak dla prądu elektrycznego, gdzie opór jest odwrotnie proporcjonalny do samego pola przekroju S.
94-ZWIĄZEK POMIĘDZY ZMIANAMI CIŚNIENIA BOCZNEGO, A WŁAŚCIWOŚCIAMI BIOMECHANICZNYMI NACZYNIA KRWIONOŚNEGO:
W naczyniach sprężystych przy wzroście ciśnienia napędowego rośnie ciśnienie działające na ściany naczynia.
Ściany naczynia rozciągają się, zmniejsza się czynnik geometryczny l/r^4, zmniejsza się opór naczyniowy.
Ciśnienie, z jakim krew działa na ściany naczynia, jest zrównoważone ciśnieniem ściany na krew. Jest ono wynikiem napięć sprężystych występujących w ścianie.
Siły rozciągające naczynia działają stycznie do cylindrycznej powierzchni naczynia i są przyłożone prostopadle do odcinków równoległych osi cylindra ryc.13.7 w Pilawskim, str.296).
Siłom tym przeciwstawiają się siły sprężyste w ścianie naczynia.
Stosunek wypadkowej F tych sił do długości L odcinka, wzdłuż którego są zaczepione, nazywa się napięciem sprężystym.
T = F / L [T] = Nm^-1
Naczynia mają także zdolność do czynnej zmiany światła ich przekroju (zdolność naczynioruchowa)-pobudzenie mięśni gładkich w ścianie naczynia powoduje ich skurcz. Podczas skurczu zmniejsza się promień naczynia.
95 - ZWIĄZEK MIĘDZY ZMIANAMI PROMIENIA TĘTNICY, A ZMIANĄ CIŚNIENIA BOCZNEGO:
Pomiędzy ciśnieniem sprężystym p, z jakim ściana naczynia cylindrycznego o promieniu r działa na ciecz, a napięciem sprężystym T istnieje zależność wyrażająca się wzorem Laplace'a:
p=T/r
ciśnienie sprężyste jest odwrotnie proporcjonalne do promienia naczynia
ciśnienie sprężyste jest proporcjonalne do napięcia sprężystego
małe naczynia potrafią przeciwstawiać się stosunkowo dużym ciśnieniom, dzięki znacznie mniejszemu promieniowi
p r = T
napięcie sprężyste T wzrasta w przybliżeniu liniowo ze wzrostem promienia dla odkształceń małych, dla odkształceń większych napięcie rośnie coraz gwałtowniej
96 - PODSTAWOWE WIELKOŚCI CHARAKTERYZUJĄCE UKŁAD KRĄŻENIA W ASPEKCIE BIOFIZYCZNYM
ciśnienie - ruch krwi jest uwarunkowany różnicą ciśnień między układem tętniczym i żylnym, utrzymywaną przez pracę serca (aorta - śr.100 mmHg, w żyłach ok.10mmHg, różnica - 90mmHg)
na ciśnienie krwi w naczyniach wpływa też ciśnieni hydrostatyczne wywołane polem grawitacyjnym, zależy ono od wysokości słupa cieczy:
p = ρgh
prędkość przepływu - wg.prawa ciągłości strumienia jest ona odwrotnie proporcjonalna do pola przekroju przewodu
Q = S v -> v = Q / S
opór naczyniowy przepływu - pyt.92
szybkość fali tętna(c):
c^2 = Ee / 2ρr
E-moduł Younga ścian naczynia
e - grubość ściany
ρ - gęstość
r - promień przekroju
praca, moc i wydajnośc serca - pyt.103
131. WŁAŚCIWOŚCI ŚWIATŁA LASEROWEGO
Światło laserowe powstaje na skutek emisji wymuszonych, więc jest monoenergetyczne. Ponadto charakteryzuje się zgodnością faz i częstotliwości. Powielone zostają jedynie fotony równoległe do luster w cylindrze, w skutek czego emitowane światło jest światłem spolaryzowanym, inaczej mówiąc wszystkie fotony drgają w jednym kierunku: są równoległe. Dzięki wszystkim tym cechom, światło laserowe możemy nazwać wiązką spójną. Równoległość i jednobarwność (zgodność częstotliwości) pozwala na zogniskowanie tego światła w bardzo małym punkcie, porównywalnym z długością fali (ryc. 18.2, str 397, Pilawski)
132 ZASTOSOWANIE LASERÓW
137 PRAWO MALUSA
Prawo Malusa definiujemy wzorem:
Io- natężenie światła padającego na nikol
I - Natężenie światła opuszczającego nikol
B eta ( we wzorze fi(?))- kąt jaki tworzy płaszczyzna światła padającego i opuszczającego nikol
Treść prawa: Natężenie światła spolaryzowanego liniowo po przejściu przez nikol jest równe iloczynowi natężenia światła padającego i kwadratu cosinusa kąta między płaszczyzną polaryzacji światła padającego a płaszczyzną polaryzacji światła po przejściu przez nikol.
139. Polarymetr Lippicha.
Polarymetr służy do pomiaru kąta skręcenia płaszczyzny polaryzacji α. Pomiarów dokonuje się dwukrotnie: raz gdy w rurce jest rozpuszczalnik i drugi raz, gdy w rurce jest badany roztwór. Różnica kątowego ustawienia analizatora w obu przypadkach jest równa kątowi skręcenia płaszczyzny polaryzacji.
Zasada działania:
Światło wychodzące ze źródła Ż przechodzi przez filtr F, zatem na polaryzator P pada światło jednobarwne, które po przejściu przez rurkę R z badanym roztworem i analizator A wpada do lunety.
139.1 Budowa polarymetru Lippicha: Ż- źródło światła; F- filtr; P- polaryzator; N- nikole; R- rurka z roztworem; A- analizator;
Przez umieszczenie za nikolem P małego nikola N otrzymujemy w lunecie dwa pola widzenia. Jedno pole widzenia jest oświetlone przez światło przechodzące przez polaryzator (pole I), drugie przez polaryzator i mały nikol (pole II).
1. 2. 3.
139.2 Względna jasność pól I i II obserwowanych w lunecie jest zależna od ustawienia analizatora w stosunku do kierunku drgań OA i OB. Linią przerywaną oznaczono kierunek drgań wyznaczony przez analizator.
Kierunek wektora OA drgań świetlnych w wiązce wychodzącej z polaryzatora P tworzy kąt γ (nie jest zaznaczony na rysunku) z linią podziału pól-taki sam jak kierunek wektora OB (wychodzący z małego nikola) z linią podziału pól.
1.Jeśli kierunek drgań wyznaczony przez analizator będzie prostopadły do wektora OA, to pole I będzie ciemne, a II jasne.
2.Natomiast gdy ten kierunek drgań będzie prostopadły do wektora OB to pole II będzie ciemne, a I jasne.
3.Wreszcie przy takim ustawieniu analizatora, przy którym kierunek wychodzącego z niego światła jest prostopadły do linii podziału pól- otrzymamy równomiernie oświetlone obydwa pola. Składowe OK i OM wektorów OA i OB są równe, a tylko światło z nimi związane przechodzi przez analizator.
Źródło: Kędzia, str. 202-203
140. Wyznaczanie stężenia za pomocą polarymetru.
Polarymetr służy do pomiaru kąta skręcenia płaszczyzny polaryzacji α.
Znając:
- kąt skręcenia płaszczyzny polaryzacji światła α przez roztwór optycznie aktywny,
- grubość warstwy roztworu l
- skręcalność właściwą [α]
możemy wyznaczyć stężenie roztworu ze wzoru: α = [α] ∙ c ∙ l
Zastosowanie: wyznaczanie stężenia glukozy w moczu u osób chorych na cukrzycę. Polarymetry służące do tego nazwane są sacharymetrami
138 BUDOWA NIKOLU
Nikol składa się z dwóch pryzmatów kalcytu: specjalnie oszlifowanych i sklejonych podstawami balsamem kanadyjskim. Balsam jest ośrodkiem optycznie rzadszym od kalcytu. (ryc. 26.3, str. 201)
142 KĄT GRANICZNY
Kąt graniczny gamma jest to taki kąt padania, przy którym przy przejściu światła z ośrodka gęstszego do rzadszego, kąt załamania jest równy 90 stopni. Po jego przekroczeniu wiązka światła ulega odbiciu.
1/sin gamma = n2,1
Gdzie:
n2,1 - względny współczynnik załamania ośrodka 2 względem ośrodka 1.
143 - Całkowite wewnętrzne odbicie
Występuje na granicy ośrodków o różnych współczynnikach załamania. Jeżeli kąt padania w ośrodku gęstszym jest większy od kąta granicznego, promień nie może przejść do ośrodka rzadszego (nie może się załamać) i na granicy ośrodków ulega całkowitemu wewnętrznemu odbiciu, odbija się pod kątem równym kątowi padania.
144. Refrakcja molekularna
Charakteryzuje cząsteczkę oraz jest związana ze współczynnikiem załamania.
Zsumowane refrakcje molekularne wszystkich wiązań równają się refrakcji molekularnej cząsteczki wówczas gdy chmury elektronowe oddziałujących ze sobą cząsteczek są od siebie niezależne, tzn. nie oddziałują ze sobą. Mówimy wówczas, że refrakcja molekularna jest addytywna. Addytywność refrakcji molekularnej wykazują związki organiczne oraz takie nieorganiczne, w których występują wiązania jonowe, np. NaCl.
Egzaltacją refrakcji molekularnej nazywamy różnicę między refrakcjami molekularnymi.
Jedną refrakcję liczymy sumując energie wiązań danego związku, drugą zaś mierzymy pośrednio poprzez pomiar współczynnika załamania oraz mając daną masę molową i gęstość danej substancji. Egzaltację molekularną możemy traktować jako pewnego rodzaju niezależność wiązań w cząsteczce. Jeżeli elektrony tworzące wiązania nie oddziałują ze sobą egzaltacja jest równa zeru, w miarę wzrostu oddziaływań egzaltacja również przyjmuje większe wartości.
Konsekwencją addytywności refrakcji wiązań są zależności jakie występują pomiędzy refrakcjami molekularnymi związków organicznych, które tworzą szeregi homologiczne. Różnica refrakcji związków, które sąsiadują ze sobą w szeregu homologicznym jest prawie niezmienna.
Wzór na refrakcję molekularną:
R = n2 - 1 M/ n2 + 2 ρ [R] = m3/mol
145.Refrakcja molekularna
Za współczynnik załamania n danej substancji odpowiedzialne są jej elektrony, a przede wszystkim elektrony walencyjne (biorące udział w tworzeniu wiązań). Ich reakcja na działania pola elektrycznego fali świetlnej decyduje o wartości współczynnika załamania danej substancji.
W związku z tym ze wiązania wpływają na wartość n wyprowadzono parametr charakteryzujący dana cząsteczkę i związany z n.
Jest to refrakcja molekularna:
Jeżeli chmury elektronowe w cząsteczce są od siebie niezależne (nie oddziałują ze sobą) to zsumowane refrakcje wszystkich wiązań równają się refrakcji molowej cząsteczki.
Dzieje się tak np. w wielu cząsteczkach organicznych oraz tych nieorganicznych w których występują wiązania jonowe. W takich przypadkach mówimy że refrakcja jest addytywna i liczymy ją jako sumę refrakcji wszystkich wiązań.
R=2*RC-H +2*RCl-C+RC=C
Refrakcje taką można również zmierzyć pośrednio mierząc współczynnik załamania światła i mając dane: masę molową i gęstość.
146. Egzaltacja
Pewne właściwości cząsteczki możemy traktować jako sumę właściwości tworzących je wiązań chemicznych. Takie podejście jest możliwe w odniesieniu do cząsteczek w których, chmury elektronowe poszczególnych wiązań są w znacznym stopniu od siebie niezależne tzn. nie oddziałują ze sobą. Wówczas zsumowane refrakcje molekularne wszystkich wiązań równają się refrakcji molekularnej cząsteczki. Mówimy, że refrakcja molekularna jest addytywna. Wykorzystując zasadę addytywności możemy obliczyć refrakcję molekularną np. dla dwuchloroetylenu C2H2Cl2. R(refrakcja wynosi) RC2H2Cl2=2*RC-H+2*RC-Cl+RC=C Gdzie z odpowiednich tablic odczytujemy potrzebne refrakcje wiązań. Podajemy ją w następującej jednostce [m3/mol]. Refrakcję możemy zmierzyć pośrednio - mierząc współczynnik załamania i mając dane: gęstość molową i gęstość badanej substancji. Ze wzoru:
R=n2-1M/n2+2d
Gdzie: d- gęstość, M- masa molowa, n- współczynnik załamania
Różnicę obu refrakcji, a właściwie jednej wyznaczonej dwoma metodami nazywamy egzaltacją refrakcji molekularnej. Można ją traktować jako pewną miarę niezależności wiązań chemicznych w cząsteczce. Gdy wiązania są od siebie niezależne, egzaltacja refrakcji jest bliska zeru; odwrotnie- jej wzrost świadczy o tym, że elektrony z różnych wiązań oddziałują ze sobą. Niezależnymi wiązaniami są wiązania pojedyncze a zależnymi wiązania wielokrotne.
147. Refraktometr Abbego
Mierząc kąt graniczny w ośrodku gęstszym o znanym współczynniku załamania n2 można wyznaczyć wsp. zał. ośrodka optycznie rzadszego n1
n1= n2 sin
Na tej zasadzie oparte jest działanie refraktometru Abbego. Jego główna częścią jest kostka złożona z dwóch prostokątnych pryzmatów p1 i p2 wykonanych ze szkła o dużym współczynniku załamania n2. Pryzmaty złożone są swoimi płaszczyznami przeciwprostokątnymi a powierzchnia dolnego pryzmatu jest matowa. Badana cześć wprowadzamy pomiędzy pryzmaty ( ciesz musi mieć n mniejsze od n szkła). Źródło światła Z kierujemy za pomocą zwierciadła L na dolny pryzmat gdzie ulega ono rozproszeniu na matowej powierzchni tak że w cieszy rozchodzi się w rożnych kierunkach. Na górny pryzmat padają promienie pod rożnymi kątami ale w pryzmacie biegną tylko w obrębie kąta granicznego. W okularze lunetki do której wpadają promienie po wyjściu z pryzmatu widzimy jasna i ciemna cześć pola widzenia (jasna oświetlona jest przez promienie w obrębie kata). Jeśli rozgraniczenie pól ustawimy za pomocą kostki przechodzącej przez punkt 0 na środek krzyża w okularze to możemy odczytać współczynnik załamania cieczy.
Jako ze współczynnik załamania światła zależy od stężenia to dla niektórych cieczy (dla takich dla których zależność współczynnika załamania od stężenia jest jednoznaczna ) wykonując pomiary współczynnika załamania światła można wykonać wykres n=f(c) dla znanych stężeń a następnie mierząc współczynnik załamania światła odczytać nieznane stężenie.
148. Aktywność optyczna
Aktywność optyczna lub czynność optyczna - właściwość niektórych związków chemicznych polegająca na zdolności skręcania płaszczyzny polaryzacji światła spolaryzowanego. Warunkiem koniecznym występowania aktywności optycznej cząsteczek jest ich chiralność, czyli istnienie w formie dwóch nienakładanych enancjomerów. Nie wszystkie cząsteczki chiralne wykazują jednak aktywność optyczną. Aby ją wykazywać w zauważalnym stopniu, chiralne cząsteczki muszą posiadać silnie spolaryzowane wiązania chemiczne blisko centrum chiralności lub posiadać przy tym centrum znacząco różne podstawniki. Skręcalność optyczna jest funkcją długości fali światła. Związki optycznie czynne mogą występować w odmianach prawoskrętnej i lewoskrętnej. Właściwość ta charakterystyczna dla wielu związków nosi nazwę izomerii optycznej i związana jest z rodzajem symetrii w budowie tych cząstek. Do związków skręcających płaszczyznę polaryzacji należą min. roztwory cukrów. Ta właściwość cukrów wykorzystywana jest w diagnostyce medycznej, gdzie za pomocą polarymetrów określa się stężenie cukrów w roztworach( głównie w moczu). Polarymetry takie nazywamy- sacharymetrami. Do optycznie aktywnych zaliczamy także roztwory wielu biopolimerów- w tym białek i kwasów nukleinowych. O aktywności optycznej tych związków decyduje zarówno asymetria budowy pojedynczych grup- merów jak i przestrzenne rozmieszczenie tych grup w łańcuchu polinukleotydowym.
149. Substancje optycznie czynne
Substancje optycznie czynne są to związki chemiczne wykazujące zdolność skręcenia płaszczyzny polaryzacji przechodzącego przez nie światła. Związki te można podzielić na 2 grupy. Pierwsza stanowią te które wykazują aktywność optyczna tylko w określonym stanie skupienia (np. krystalicznym- chloran sodowy). Druga obejmuje substancje wykazujące aktywność optyczna niezależnie od stanu skupienia - np. prawie wszystkie biopolimery. Musza one charakteryzować się posiadaniem jednej z dwóch cech: chiralnością lub brakiem elementów symetrii.
Chiralność oznacza ze związek chemiczny może występować w formach enancjomerycznych natomiast brak symetrii odnosi się najczęściej do związków zawierających asymetryczny atom węgla. Związki optycznie czynne wykazują wobec światła spolaryzowanego dwójłomność kołową. Oznacza to ze fale spolaryzowane w prawo i lewo rozchodzą się z rożnymi prędkościami. Jeżeli jedna wyprzedza druga to w roztworze występuje skręcenie płaszczyzny polaryzacji o kat
=[] * c * l
Gdzie: - skręcalność właściwa przy długości fali
l - długość drogi optycznej
c - stężenie
Dodatkowo dla niektórych związków chemicznych []= f() ma postać monotonicznie zmniejszającej się wartości [] wraz ze wzrostem długości fali. Przebieg zależności wykazuje zdecydowana odmienność jeżeli związek chemiczny charakteryzuje się w zakresie użytych długości fal występowaniem pasm absorpcyjnych. W takim ośrodku fale spolaryzowane kołowo nie tylko rozchodzą się z rożnymi prędkościami ale są tez w rożnym stopniu pochłaniane. Taki ośrodek wykazuje dichorizm kołowy ( wynik efektu Cottona)
150. Aberracje chromatyczne i sferyczne
Aberracja chromatyczna - Obrazem punktu nie jest punkt, ale obszar trójwymiarowy w którym strumień światła jest niejednorodny i w dodatku barwny. Związane jest to z tym, że prędkość rozchodzenia się światła tylko w próżni jest niezależna od częstotliwości, czyli od barwy. Współczynnik załamania światła a więc i ogniskowa są zależne od barwy światła. Jeśli punkt wysyła światło białe to układ optyczny wytworzy ciąg obrazów, gdzie obraz utworzony przez promienie fioletowe będzie najbliżej od układu a utworzony przez promienie czerwone - najdalej od układu. Powiększenie układu także zależy od barwy promieni i jest różne dla różnych barw. Zjawiska te nazywamy aberracjami chromatycznymi położenia i powiększenia i są spowodowane dyspersją czyli zależnością współczynnika załamania od częstotliwości. Miarą dyspersji jest współczynnik dyspersji, który jest różny dla różnych rodzajów szkła co jest wykorzystywane do korekcji aberracji chromatycznych w układach optycznych. Korekcja: pokrycie ogniska utworzonego przez promienie fioletowe i ogniska utworzonego przez promienie czerwone w układzie złożonym z dwóch soczewek dodatniej i ujemnej tak żeby wartość bezwzględna zdolności skupiającej soczewki dodatniej były np. dwa razy większe niż ujemnej, a współczynnik dyspersji szkła soczewki dodatniej dwa razy mniejszy niż ujemnej. Taki układ jest achromatyczny(pierwszy stopień korekcji chromatyzmu).
Aberracja sferyczna - Jeżeli promień biegnie poza obszarem przyosiowym wówczas ogniskowa jest zależna od wysokości h, im większe h tym krótsza ogniskowa. Aberracja sferyczna jest miarą wady układu optycznego, jej miarą jest odległość między ogniskiem dla promieni przyosiowych a ogniskiem dla promieni skrajnych dla h maks. Aberracja sferyczna jest aberracja osiową - dotyczy obrazów punktów lezących na osi. Aberracja dotyczaca obrazów punktów lezących poza osia nazywa się koma.
Aberracja pozaosiowe: astygmatyzm, krzywizna pola i dystorsja.
Astygmatyzm rośnie z kątem ω( kąt między promieniem padającym a osia optyczną). Jego miarą jest różnica zdolności skupiającej w dwóch przekrojach głównych : południkowym i równoleżnikowym. Im bardziej skośna wiązka tym większa różnica zdolności skupiającej między tymi przekrojami. Przekrój południkowy jest wyznaczany przez płaszczyznę południkową zawierającą oś wiązki i oś optyczną, przekrój równoleżnikowy jest wyznaczany przez płaszczyzną równoleżnikową prostopadła do poprzedniej i zawierającą oś wiązki światła. W tych przekrojach promienie krzywizn są różne.
Krzywizna pola - obszar płaszczyzny jest powierzchnią krzywą.
Dystorsja - powiększenie P układu zmienia się z kątem ω, obrazem siatki kwadratowej ma kształt poduszki przy rosnącym P wraz ze wzrostem ω lub beczki przy malejącym P.
151. Układ optyczny oka
Układ optyczny:- jest to każdy przeźroczysty obszar z przestrzennym rozkładem współczynnika załamania n=f(x,y,z).
Jest szerszym pojęciem niż soczewka, ponieważ obejmować może soczewkę, układ soczewek, układ układów optycznych (mikroskop).
Elementarnym układem optycznym jest powierzchnia załamująca (np. soczewka składa się z 2 powierzchni załamujących).
Zadanie układu optycznego:- przekształcenie przestrzeni przedmiotowej (zbioru punktów tworzących przedmioty) w przestrzeń obrazową (zbiór punktów tworzących obrazy tych przedmiotów).Więc każdy punkt przedmiotowy ma odpowiadający mu punkt obrazowy wyjątek:-ogniska. Ognisko obrazowe NIE jest obrazem ogniska przedmiotowego.
Układ optyczny oka
składa się z: rogówki i soczewki ocznej. Ponieważ ośrodki optyczne graniczące z nimi są różne to ogniskowe obrazowa i przedmiotowa też są różne.
przesłoną aperturową jest tęczówka.
ma wyjątkową soczewkę ponieważ jej współczynnik załamania jest różny w poszczególnych warstwach(jądro-1,40; warstwy zewn.-1,33).
przez różne napięcie mięśnia soczewki, staje się ona bardziej lub mniej wypukła= zmienna zdolność skupiająca oka przy stałej odległości ukł. optycznego oka od siatkówki umożliwia tworzenie na siatkówce obrazów przedmiotów dalekich i bliskich= akomodacja.
152. Próg czułości oka
Żeby wywołane zostało wrażenie wzrokowe do oka musi być dostarczona określona porcja energii świetlnej, nie mniejsza od bezwzględnego progu czułości oka. Dla przeciętnego oka wynosi on 4x10-17 J co odpowiada około 100 kwantom. Bezwzględny próg czułości siatkówki wynosi 1-8 kwantów.
Aby wywołać wrażenie wzrokowe do oka musi dotrzeć określona ilość światła nie mniejsza od bezwzględnego progu czułości oka . W celu określenia bezwzględnego progu czułości oko które uprzednio jest zaadaptowane do ciemności poddaje się krótkim błyskom świetlnym zwiększając stopniowo energię tych błysków aż do momentu gdy pierwszy z nich zostanie zauwżony.
Jeżeli za 100 kwantów przyjmiemy 100% to w wyniku odbicia światła od ośrodków przeziernych do oka dotrze 40% z czego absorbowanych jest 20% czyli 8kwantów. Zatam bezwzględny próg czułości siatkówki wynosi 8 kwantów. Kwanty te nie padają na 1 pręcik tylko na grupę pręcików można przyjąć że 1 kwant powoduje pobudzenie 1 pręcika . Za pomocą rachunku statystycznego Pirenne potwierdził porównując wartości teoretyczne z doświadczalnymi, że bezwzględny próg czulości ma wartość 1-8 kwantów.
153. Refrakcja oka
Refrakcją oka R nazywamy odwrotność odległości SD punktu dalekiego D od oka
R=1/SD
Refrakcja jest mierzona w dioptriach. Gdy refrakcja oka jest równa 0 mówi się że oko jest miarowe wówczas punkt daleki od oka miarowego jest w nieskończoności. W przypadku gdy refrakcja oka nie jest równa 0 to oko obarczone jest wadą krótko lub dalekowzroczności. Zatem miarą wad wzroku jest refrakcja R
154. Zdolność skupiająca przedniej części rogówki. ???
Rogówka jest jednym z ośrodków przeziernych oka ograniczających ilość światła dochodzcego do siatkówki. Powoduje załamywanie promieni świetlnych. Jest soczewką wypukło-wklęsłą. Współczynnik załamania światła wynosi 1,376
155. Akomodacja oka
Akomodacja oka to zdolność tworzenia się na siatkówce obrazów przedmiotów zarówno bliskich i dalekich mimo praktycznie stałej odległości układu optycznego oka od siatkówki dzięki temu ze oko posiada zmienną zdolność skupiającą (wynika ona ze zmiany kształtu soczewki a co za tym idzie jej ogniskowej).
Ma ona pewien skończony zakres, wyznaczony przez zdolność do odwzorowania ostro na siatkówce obszaru między osiowymi punktami dalekim i bliskim. Obraz pierwszego jest utworzony na siatkówce gdy zdolność skupiająca oka jest najmniejsza, a drugiego gdy jest ona maksymalna.
156. Starczowzroczność
Starczowzroczność to proces zwężania zakresu akomodacji, który wywoływany jest przez sztywnienie w raz z wiekiem soczewki ocznej. Wynikiem tego przy stałym położeniu punktu dalekiego D punkt bliski B oddala się od oka np. dziecko punkt bliski ma w odległości kilku cm od oka natomiast człowiek 50-letni około pół metra.
Proces ten nie zmienia refrakcji oka.
Korekcja starczowzroczności polega na tym aby obraz punktu bliskiego oka został ustawiony przez tę soczewkę w odległości dogodnej do pracy.
157. Krótkowzroczność. Korekcja
Krótkowzroczność jest jedną z najczęściej spotykanych wad refrakcyjnych wzroku polegającą na tym, że tor optyczny oka nieprawidłowo skupia promienie świetlne. Promienie równoległe, które w akomodującym oku miarowym ogniskowane są na siatkówce, w nieakomodującym oku krótkowzrocznym ogniskowane są przed siatkówką.
Obraz na siatkówce w krótkowzroczności jest zamazany, a wrażenie wzrokowe krótkowidza jest nieostre. Żeby dobrze zobaczyć przedmiot krótkowidz przysuwa go bliżej oczu. Krótkowidz patrząc na obiekty odległe nie może pomóc sobie akomodacją, jak to czyni dalekowidz. Jeśli jednak jest wystarczająco jasno to pomaga sobie mrużąc oczy, zmniejszając rozproszenie obrazu na siatkówce poprzez zwiększenie głębi ostrości. W celu poprawy ostrości widzenia krótkowidza stosuje się okulary korekcyjne lub soczewki kontaktowe. Są to soczewki rozpraszające wklęsło-wypukłe. Ich moc optyczną podaje się w dioptriach dodając znak minus. Możliwy jest również zabieg chirurgiczny (bardzo duża skuteczność, możliwe ciężkie efekty uboczne).
158. Dalekowzroczność, korekcja
Oko jest miarowe jeżeli refrakcja oka jest równa zero, czyli sD = ∞, siatkówka jest styczna do ogniskowej oka nieakomodującego, punkt D jest w nieskończoności. Jeżeli ten warunek nie jest spełniony to wówczas mamy do czynienia z wadą wzroku. Promienie równoległe, które w nieakomodującym oku miarowym ogniskowane są na siatkówce, w nieakomodującym oku nadwzrocznym ogniskowane są za siatkówką. Refrakcja jest większa od zera i sD jest większe od zera.
Korekcja polega na dobraniu takich soczewek żeby obraz punktu nieskończenie odległego utworzonego przez tą soczewkę pokrywał się z punktem dalekim oka. Czyli soczewkę która po ustawieniu przed okiem miałaby ognisko obrazowe w punkcie dalekim oka. Wtedy płaszczyzna ogniskowa obrazowa układu soczewka korekcyjna + układ optyczny oka jest styczna do siatkówki oka nieakomodującego. Zdolność skupiająca soczewki Dk
Dk =R/ (1 - lR)
Gdzie: l to odległość soczewki od oka R - refrakcja oka
Przy dalekowzroczności │ Dk │< │R│
159. Punkty kardynalne, rola
W układzie optycznym mamy 6 punktów kardynalnych:
1)dwa ogniska- F i F'
2)dwa punkty główne H i H'są to punkty przecięcia płaszczyzny głównej przedmiotowej i obrazowej z osią optyczną.
3)dwa punkty węzłowe K i K'są to punkty osi optycznej spełniające warunek: Gdy kierunek promienia padającego pod pewnym kątem do osi optycznej przechodzi przez punkt węzłowy przedmiotowy, to kierunek promienia załamanego przechodzi przez punkt węzłowy obrazowy i jest nachylony pod tym samym kątem do osi.
Gdy współczynnik załamania w ośrodku przed i za układem jest taki sam to pkt. węzłowe pokrywają się z pkt. głównymi.
Dla oka pkt. węzłowe NIE pokrywają się z pkt. głównymi
ROLA pkt. kardynalnych:znając ich położenie możemy jednoznacznie ustalić bieg promieni przez układ. Są one potrzebne do wyznaczenia parametrów (wielkość i położenie) obrazu utworzonego przez ten układ.
160. płaszczyzna obrazowa i przedmiotowa
Gdy nie można określić środka układu optycznego rzeczywistegonie można ustalić długości ogniskowej i wykreślić biegu promieni przez układwprowadzamy pojęcie płaszczyzn głównych.
*Płaszczyzna główna obrazowa-zbiór punktów M' gdzie przecinają się:
1)przedłużenia promieni padających równolegle do osi z
2)przedłużeniami odpowiednich promieni załamanych.
Miejsce przecięcia jest w ognisku obrazowym F';
*Płaszczyzna główna przedmiotowa-zbiór punktów M gdzie przecinają się:
1)przedłużenia promieni załamanych i biegnących dalej równolegle do osi z
2)przedłużeniami odpowiednich promieni padających.
Miejsce przecięcia jest w ognisku przedmiotowym F.
Odległość między tymi dwiema płaszczyznami jest zawsze dodatnia (układ skupiający i rozpraszający).
Punkty H i H' przecięcia tych płaszczyzn z osią optyczną to punkty główne układu optycznego.
Ogniskowa obrazowa:- to odległość między pkt. H' i F' (ogniskiem obrazowym).
Ogniskowa przedmiotowa:- to odległość między pkt. H i F (ogniskiem przedmiotowym).
Układ skupiający- ma ogniskową obrazową- dodatnią.
Układ rozpraszający- ma ogniskowa obrazową- ujemną.
161.
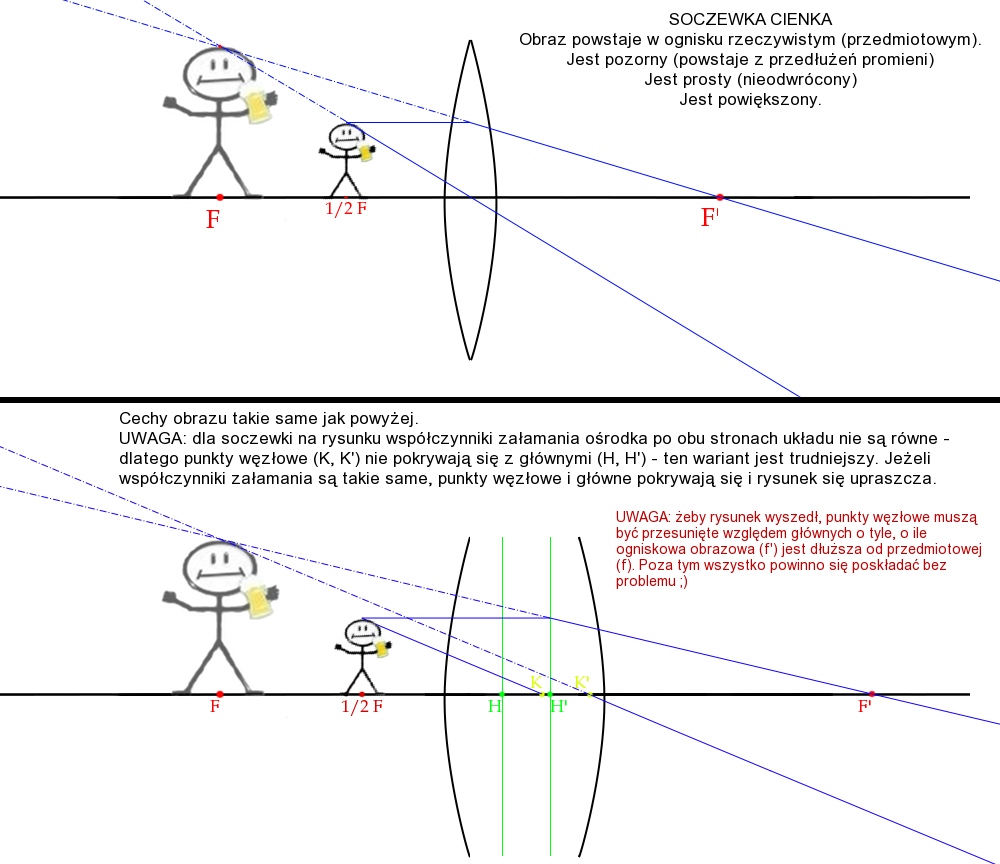
162.
Układ optyczny oka składa się z rogówki i soczewki ocznej, przy czym ośrodki optyczne (powietrze, ciecz wodnista i ciało szkliste) graniczące z tymi elementami są różne. Stąd ogniskowe obrazowa i przedmiotowa są różne. Przesłoną aperturową oka jest tęczówka. Układ optyczny oka spośród innych wyróżnia wyjątkowa soczewka. Współczynnik załamania jest różny w poszczególnych jej warstwach, w jądrze wynosi 1,40 a w warstwach zewnętrznych 1,33. Nadto przez różne napięcie mięśnia soczewki, soczewka staje się bardziej lub mniej wypukła. Dzięki temu zdolność skupiająca oka jest zmienna, co pozwala na tworzenie na siatkówce obrazów przedmiotów bliskich i dalekich.
Ciecz wodnista - substancja wypełniająca przednią komorę oka. Występuje w ilości ok. 0,3 cm³ w każdej gałce ocznej. Przeźroczysta ciecz wytwarzana w tylnej komorze oka w wyrostku rzęskowym w ilości ok. 2 mm³/min.. Przez źrenicę dostaje się do komory przedniej oka. Stamtąd nadmiar cieczy wodnistej jest odprowadzany kanałem Schlemma do układu żylnego. Ciecz wodnista odprowadza szkodliwe produkty przemiany materii oraz odżywia rogówkę i soczewkę. Współczynnik załamania n=1336.
Rogówka- wypukła zewnętrzna warstwa gałki ocznej w jej przedniej części. Ludzka rogówka ma ok. 11,5 mm średnicy i grubość 0,5-0,6 mm w środkowej części oraz 0,6-0,8 mm w części obwodowej. Za rogówką znajduje się ciecz wodnista a za nią soczewka. Rogówka nie jest unaczyniona, naczynia upośledzałyby jej przezierność. Odżywia się dzięki dyfuzji - przez łzy i ciecz wodnistą gałki ocznej, a także dzięki neurotrofinom dostarczanym przez unerwienie rogówki. Posiada dużo zakończeń bólowych, włókien bezrdzennych. Rogówka silnie skupia promienie świetlne (ok. 43 D), bardziej niż soczewka (ok. 20 D). Jednak w przeciwieństwie do soczewki, siła skupiania promieni przez rogówkę jest stała (nie podlega regulacji). Współczynnik załamania n=1,376
Ciało szkliste- galaretowata substancja wypełniająca tylną część gałki ocznej, nadająca jej kształt i chroniąca siatkówkę. Współczynnik załamania n=1,336
163 powierzchnia załamująca
Bieg promienia przez sferyczną powierzchnię załamującą oddzielającą 2 ośrodki o różnych współczynnikach załamania:
Pojedyncza powierzchnia sferyczna o promieniu krzywizny r jest w stanie skupić wiązkę rozbieżnych promieni- a więc utworzyć obraz.
Dla promieni przyosiowych (gdy h jest bliskie zeru): sin i ≈ i oraz sin i'≈ i' , z prawa załamania światła ( n sin i = n' sin i' ) możemy zapisac ni = n'i' gdzie: i jest kątem padania, i'- kątem załamania
Kąt i (zewnętrzny trójkąta ADO) i= u + ρ
Kąt i' i'= ρ - u'
Podstawiając do wzoru => n(ρ+u) = n'(ρ-u')
Ponieważ h jest bardzo małe: ρ=h/r; u=h/s; u'=h/s'
=> n (h/r + h/s) = n' (h/r - h/s') (dzielimy przez h) => n'/s' - n/s = (n'-n)/r
-przecięcie promienia z osią w przestrzeni obrazowej= ognisko obrazowe (s'=f', n/∞=0)
f'=
-przecięcie promienia z osią w przestrzeni przedmiotowej= ognisko przedmiotowe (n'/∞=0, s=f)
f= -
-odległość zredukowana- długość geometryczna podzielona przez współczynnik załamania ośrodka l zred= l/n (odległość jaką ten odcinek miałby w próżni- w praktyce w powietrzu)
164. Ognisko przedmiotowe i obrazowe
układ skupiający (dodatni)
Ognisko obrazowe to punkt, w którym skupia się równoległa
wiązka promieni padających na układ optyczny po jego przejściu.
Ognisko przedmiotowe- pkt. z którego wychodzą promienie padające, które po przejściu przez powstaje wiązka promieni równoległych.
układ rozpraszający (ujemny)
Ognisko obrazowe- to punkt, w którym skupiają się przedłużenia
promieni wychodzących z układu, gdy na układ pada wiązka promieni równoległych
Ognisko przedmiotowe - pkt. z którego wychodzą przedłużenia promieni padających gdy po przejściu przez układ powstaje wiązka promieni równoległych
Ogniska obrazowe i przedmiotowe leżą zawsze po dwóch różnych stronach soczewki: dla soczewki dodatniej ognisko przedmiotowe F leży przed soczewką, a obrazowe F' leży za soczewką, dla soczewki zaś ujemnej położenie ogniska jest odwrotne - ognisko przedmiotowe leży za soczewką, a obrazowe - przed nią.
Obydwa ogniska soczewki dodatniej (cienkiej) są rzeczywiste, soczewki zaś ujemnej {cienkiej) są pozorne. Ogniska przedmiotowe F i obrazowe F' leżą w równych odległościach od soczewki cienkiej.
Ogniskowa- odległość od punktu głównego(przedmiotowego/obrazowego) do ogniska(przedmiotowego/obrazowego).
165. Zdolność skupiająca układu optycznego prostego i złożonego, definicje, wzory, jednostki.
Zdolnością skupiającą D układu optycznego (inaczej moc optyczna) nazywamy odwrotność jego ogniskowej obrazowej.
Wzór:
Jednostka:
Domyślnie wzór ten stosuje się dla powietrza. Jeżeli dana soczewka znajduje się w ośrodku materialnym (np. olej imersyjny), którego współczynnik załamania wynosi n, zdolność skupiającą wyraża wzór
.
Dla układu optycznego złożonego stosuje się zasadę sumowania zdolności skupiającej dla dwóch powierzchni:
gdzie
- zredukowana zdolność skupiająca powierzchni załamujących
- zredukowana odległość między powierzchniami załamującymi (jest to długość geometryczna odcinka podzielona przed współczynnik załamania ośrodka, w którym ten odcinek mierzono)
166:Metoda geometryczna pomiar zdolności skupiającej:
Odwrotność ogniskowej mowi o tym w jakim stopniu układ otyczny zmienia zbieżność światła, czyli jest miara zdolności skupiającej.
Zdolność skupiająca układu lub danej soczewki. to odwrotność ogniskowej i jest ona mierzona w dioptriach [D]= 1/m
gdzie D - zdolność skupiająca, f - ogniskowa.
Zdolność skupiająca układu optycznego jest funkcją zdolności skupiających jego powierzchni załamujących oraz wzajemnych odległości miedzy tymi powierzchniami.
Zdolność skupiająca układu optycznego:
D1+2= D1+D2- lz x D1 x D2
D1 i D2-zredukowana zdolność skupiająca powierzni załamujących
Lz - zredukowana odległość miedzy powierzchniami załamującymi
x- znak mnożenia
Jest to wzór ogólny dla układu soczewek.
Wnioski ze wzoru
1)dwa układy optyczne o zdolnościach skupiających równych co do wartości a odwrotnych co do znaku, są od siebie oddalone i maja zawsze zdolność skupiająca dodatnia
2) w przypadku korygowania wad wzroku: łączna zdolność skupiajaca soczewki i oka może być zbyt mała lub zbyt duza. Im wiksza jest zdolność skupiająca soczewki korekcyjnej, tym bardziej czuła jest korekcja na zmiany odległości
Gdy soczewka znajduje się w powietrzu to:
n1=n2=1=n
1/f'=D= (n-1) (1/r1-1/r2)
Gdzie r1 i r2 to promienie krzywizny odpowiednich soczewek
Dodatnia zdolność zbierająca oznacza soczewkę lub układ optyczny skupiający, a ujemna - soczewkę lub układ rozpraszający. Zerowa zdolność zbierająca oznacza brak zmiany kierunku promieni po przejściu przez soczewkę (obie powierzchnie robocze płaskie i równoległe do siebie - może wystąpić najwyżej przesunięcie równoległe, gdy kąt padania promieni będzie różny od zera).
167. WADY SOCZEWEK, PRZYCZYNY
a) aberracja chromatyczna położenia - prędkość światła zależy od częstotliwości (barwy), z tego wynika, że współczynnik załamania jest zależny od barwy, a ogniskowa jest różna dla różnych barw. Jeśli punkt wysyła światło białe to układ optyczny tworzy ciąg obrazów. Najbliżej od układu będzie obraz utworzony przez promienie fioletowe, a najdalej obraz utworzony przez promienie czerwone.
Rysunek: Pilawski Ryc. 12.6 a; strona 261
b) aberracja chromatyczna powiększenia - spowodowana dyspersją (zależnością współczynnika załamania od częstotliwości - opisane przy aberracji położenia). Jeżeli punkt wysyła światło białe to obraz utworzony przez promienie fioletowe będzie najmniej powiększony. Najbardziej powiększony będzie obraz utworzony przez promienie czerwone.
Rysunek: Pilawski Ryc. 12.6 b; strona 261
c) aberracja sferyczna - ogniskowa jest zależna od wysokości h w ten sposób, że im większe h, tym krótsza ogniskowa. Aberracja ta powoduje, że im większy jest otwór, przez który wpadają promienie, tym większa plamka. Jest aberracją osiową, czyli dotyczy obrazów punktów leżących na osi układu.
Rysunek: Pilawski Ryc. 12.7; strona 262
d) koma - aberracja sferyczna dotycząca przedmiotów leżących poza osią układu. Dla punktów leżących poza osią obraz punktu stanowi plamka przypominająca wyglądem kometę.
e) astygmatyzm - gdy światło biegnie pod pewnym kątem do osi optycznej powierzchnia sferyczna stanowi dla wiązki świtała powierzchnię asferyczną (np. jeśli światło pada na wycinek kuli, czyli powierzchnię sferyczną, to część oświetlona jest widziana przez wiązkę światła jako niesferyczna). Im bardziej skośna jest wiązka, tym większa różnica zdolności skupiającej między przekrojem południkowym, a równoleżnikowym. Przekrój południkowy jest wyznaczony przez płaszczyznę południkową zawierająca oś wiązki i oś optyczną, a przekrój równoleżnikowy jest wyznaczony przez płaszczyznę równoleżnikową i zawierającą oś wiązki światła. Miarą astygmatyzmu jest różnica zdolności skupiającej w dwóch przekrojach głównych (południkowym i równoleżnikowym). Astygmatyzm jest aberracją pozaosiową rosnącą wraz ze wzrostem kąta padania wiązki (w stosunku do osi optycznej) - ω
Rysunek: Pilawski Ryc. 12.9; strona 263
f) krzywizna pola - aberracja pozaosiowa, powoduje, że obraz płaszczyzny jest powierzchnią krzywą
g) dystorsja - aberracja pozaosiowa, sprawia, że powiększenie P układu zmienia się z kątem padania światła względem osi optycznej (ω). Obraz siatki kwadratowej przy rosnącym P wraz ze wzrostem ω ma kształt poduszki, przy malejącym ω ma kształt beczki.
168. Zdolność rozdzielcza liniowa, kątowa.
Każdy układ optyczny charakteryzuje zdolność rozdzielcza (d) definiowana jako odwrotność najmniejszej odległości (a) dwóch punktów widzianych jeszcze oddzielnie.
d = =
A- Apertura
λ- długość fali
Dla oka wygodniej posługiwać się ZDOLNOŚCIĄ ROZDZIELCZĄ KĄTOWĄ, która stanowi odwrotność kąta α pod jakim widziane są ze źrenicy wejściowej obrazy dwu punktów jeszcze przez układ optyczny rozdzielonych.
α =
d =
gdzie :
-średnia źrenicy wejściowej
λ- długość fali
Zdolność rozdzielcza zależy od budowy układu optycznego, a także od czułości receptora i wielkości jego powierzchni.
169 . Zdolność rozdzielcza - odwrotność najmniejszej odległości dwóch punktów widzianych jeszcze oddzielnie:
d = 1/a = 2A/1,22
gdzie:
A = apertura
= długość fali
Dla oka wygodniej stosuje się zdolność rozdzielczą kątową - odwrotność kąta , pod jakim widziane są ze źrenicy wejściowej obrazy dwóch punktów jeszcze rozdzielonych.
Przyjmując kryterium Rayleigha, kąt :
= 1,22/dź dź = średnia źrenicy wejściowej
stąd:
d=1/ = dź/1,22
( przykład )
Kąt widzenia dla:
dź = 3 mm
= 600 nm
0,28 x 10 -3 rad 1'
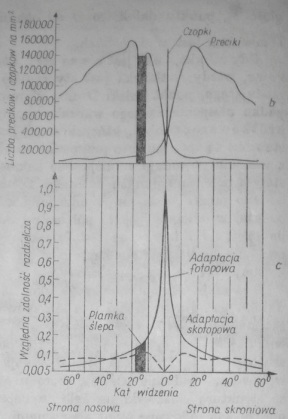
Zdolność rozdzielcza oka zależy od:
Zdolność rozdzielcza oka jest największa w plamce żółtej.
(patrząc, tak ustawiamy oko, by obraz właśnie tam się pojawił)
W przypadku siatkówki:
Mamy dwa punkty rozdzielane przez układ optyczny:
Głębia ostrości - obrazy przedmiotów w pewnej odległości od układu są widziane jednakowo dobrze - pewien wycinek przestrzeni trójwymiarowej zostaje przekształcony w przestrzeń dwuwymiarową (telewizja itd.)
Czynniki ograniczające dopływ światła do soczewki:
170. Kryterium Rayleigha, wzór, rysunek
170. W przestrzeni znajdują się dwa jednakowe punktowe źródła światła,które zbliżają się do siebie prostopadle względem osi optycznej. Przy znacznej odległości względem siebie otrzymujemy dwa obrazy dyfrakcyjne. W trakcie dalszego zbliżania w pewnym momencie obrazy zaczną się na siebie wzajemnie układać i będzie się dało zaobserwować sumowanie natężeń światła. Ciężko będzie stwierdzić czy jest to jedno niepunktowe źródło światła czy dwa punktowe. Gdy maksimum główne jednego obrazu dyfrakcyjnego leży w miejscu minimum I-rzędu drugiego obrazu, to minimum powstałe pomiędzy maksimami nie może stanowić więcej niż 0.735 natężenia maksima - wtedy źródłem są dwa punktowe źródła światła - kryterium Rayleigha.
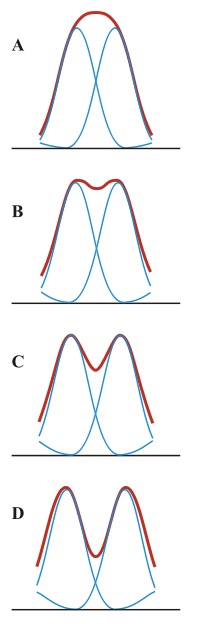
#A - dwa maksima dyfrakcyjne leżą tak blisko siebie, że linie zlewają się w jedną - są nierozróżnialne;
#B - linie są bardzo trudno rozróżnialne;
#C - spełnione jest kryterium Rayleigha (maksimum pierwszej linii pokrywa się z minimum drugiej) - linie są rozróżnialne;
#D - linie są wyraźnie rozróżnialne.
Dla obrazów dyfrakcyjnych powstałych po przejściu światła przez otwór kołowy warunek Rayleigha można zapisać wzorem
![]()
gdzie:
φ - minimalny kąt między promieniami, których obrazy mają być rozróżnialne, czyli inaczej - ich odległość kątowa;
λ - długość fali światła;
d - średnica otworu.
Ponieważ kąt φ jest bardzo mały, można zapisać w przybliżeniu:
![]()
171. Energetyka procesu widzenia
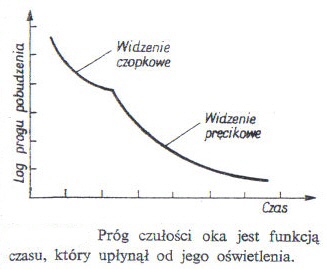
Bezwzględny próg czułości jest to najmniejsza porcja energii, jaka musi dotrzeć do oka, żeby wywołać wrażenie zmysłowe. W tym celu przeprowadzono doświadczenie, w którym eksponuje się zaadoptowane do ciemności oko na krótkie błyski światła , o długości fali odpowiadającej maksimum widmowej czułości oka przy adaptacji ciemnej. Następnie stopniowo zwiększano energię kolejnych błysków, przy pierwszym zauważonym można zmierzyć jego energię. Na podstawie takich pomiarów ustalono, że bezwzględny próg czułości dla przeciętnego oka wynosi 4*10-17 J (λ=510 nm; 100 kwantów). Obliczono także bezwzględny próg czułości dla siatkówki i wynosi on 8 kwantów, a dla pojedynczego pręcika 1 kwant (kwant energii pada na grupę receptorów).
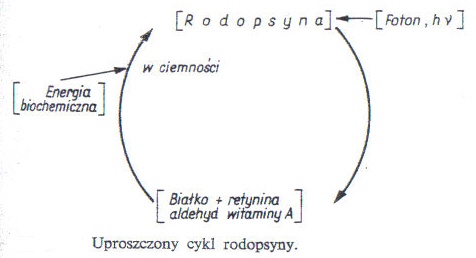
Mechanizmy adaptacyjne to możliwości przystosowania oka do zmiennych warunków, np. adaptacja do natężenia oświetlenia, barwa światła itd. Wśród nich wyróżniono automatyczną regulację średnicy źrenicy i przystosowanie się receptorów światłoczułych. Czopki charakteryzują się małą czułością na światło, potrzebne jest obfite oświetlenie - widzenie jasne (fotopowe), a pręciki odpowiedzialne są za widzenie ciemne (skotopowe). Absorpcja światła w widzeniu ciemnym powoduje rozkład rodopsyny. Wzrost natężenia światła powoduje zmniejszanie ilości rodopsyny, a tym samym zmniejszenie czułości pręcików, działa to na zasadzie ujemnego sprzężenia zwrotnego. Potwierdza to krzywa absorpcji światła przez rodopsynę w funkcji długości fali z krzywą wrażliwości widmowej w widzeniu ciemnym. Natomiast przy zaadoptowaniu oka do jasności krzywa ma przesunięte maksimum w kierunku fal dłuższych względem maksimum wrażliwości widmowej w widzeniu ciemnym. Dlatego inaczej oceniamy względną jasność dwóch przedmiotów o odmiennej barwie przy adaptacji jasnej i inaczej przy adaptacji ciemnej.
Na podstawie badań wysunięto wnioski, że wszelkie wrażenia barwne można wywołać ze pomocą odpowiednio dobranych trzech długości fal, tym samym istnieją trzy rodzaje czepków (pierwsza teoria widzenia barwnego). W dalszym ciągu przeprowadza się szereg doświadczeń, mających na celu poznanie mechanizmu widzenia barw. Pewnym jest, że nie wystarczy jeden rodzaj receptorów oraz oko zaadoptowane do ciemności nie widzi barw.
172. Widzenie przestrzenne
Patrząc jednym okiem, potrafimy rozróżniać do pewnego stopnia głębię obrazu (ponieważ mózg bierze pod uwagę takie elementy jak cienie, zasłanianie jednych przedmiotów przez drugie czy rozmazanie odległych obiektów), jednak precyzyjna ocena odległości wymaga współpracy obu oczu.
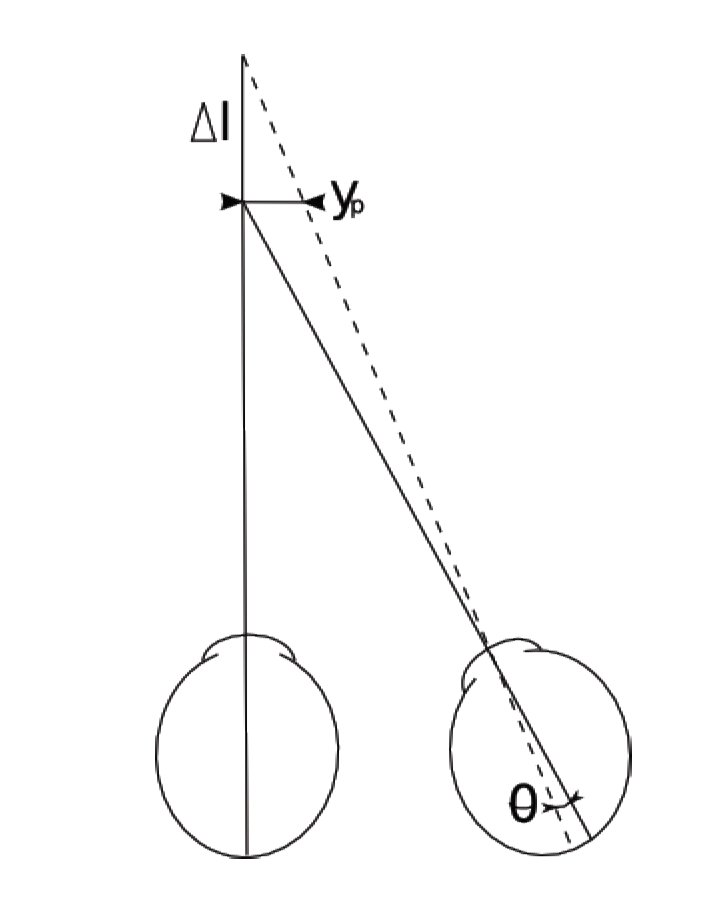
Powyższe zależności w zupełności pozwalają mózgowi uzyskiwać informacje o położeniu obiektów w przestrzeni trójwymiarowej.
173.Bieg promieni w mikroskopie
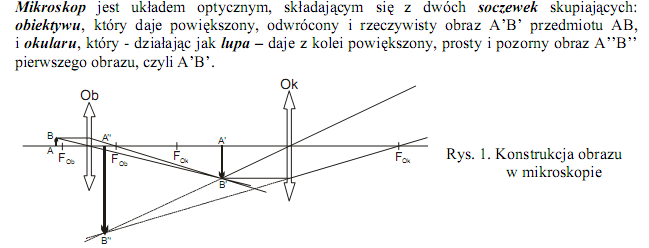
174. OBLICZENIE APERTURY MIKROSKOPU
a) obliczenie kąta aperturowego ze wzoru
tgu=m/2h
m - szerokość pola widzenia
h - grubość krążka
b) z tangensa obliczyć sam kąt, a następnie jego sinus
c) obliczenie apertury numerycznej ze wzoru
A= n sin u
d) obliczenie zdolności rozdzielczej mikroskopu ze wzoru
Z= 2A/ 1,22λ
λ - długość fali (w ćwiczeniu trzeba było przyjąć, że λ =0,55μm)
e) obliczenie powiększenia użytecznego (optymalnego) mikroskopu
Puż=1000 A
W praktyce nie stosuje się powiększeń większych od powiększenia użytecznego, bo nie pozwalają one dostrzec żadnych szczegółów oglądanego preparatu. (Komentarz z instrukcji :P)
f) obliczenie optymalnej (użytecznej) wartości powiększenia okularu
Puż, ok=Puż/Pob
Pob - powiększenie obiektywu
175. Zdolność rozdzielcza mikroskopu
Powiększenie mikroskopu jest funkcją ogniskowych obiektywu i okularu:
gdzie
- powiększenie odpowiednio obiektywu i okularu
- ogniskowe odpowiednio obiektywu i okularu w metrach
- długość tubusa w metrach
Teoretycznie zmniejszając odpowiednio ogniskowe można by uzyskać dowolnie duże powiększenie. Jednak możliwości techniczne stawiają barierę i dlatego maksymalne wykorzystywane powiększenia to ok. 1500x ( powiększenie obiektywu do 100x i okularu do 15x). Dalsze powiększenie pociągałoby również zmniejszenie pola widzenia ze względu na konieczność korekcji aberracji. Zatem otrzymalibyśmy mniejszy wycinek obrazu bez nowych szczegółów.
Zdolność rozdzielczą mikroskopu przy obserwacji preparatu można wyrazić wzorem
gdzie
a - stała granicznej siatki dyfrakcyjnej (czyli takiej, której rysy jeszcze mikroskop rozdzieli).
n - współczynnik załamania
λ - długość fali
Wynikające z tego wzoru wnioski:
Niestety w obydwu przypadkach są ograniczenia. W pierwszym przypadku nie uda się zwiększyć rozdzielczości nawet dwukrotnie, w drugim zwiększymy zdolność rozdzielczą mniej niż 10x.
Co dalej? Można wykorzystać dualizm korpuskularno-falowy i użyć elektronów - czyli mikroskop elektronowy. Tutaj długość fali λ zgodnie z twierdzeniem de Broglie'a wynosi
gdzie
h - stała Plancka
m - masa elektronu
v - prędkość elektronu
Jak duży jest zysk? Mikroskopy elektronowe pozwalają na powiększenie rzędu miliona razy i mają zdolność rozdzielczą 1000x większą niż mikroskopy świetlne.
176. Osiągnięcie powiększenia przedmiotowego jest podstawowym zadaniem mikroskopu.
Powiększenie przedmiotowe jest funkcją ogniskowych obiektywu i okularu - wykonując krótkoogniskowe układy optyczne, można uzyskać dowolnie duże powiększenie - miałoby to sens wtedy, gdy powiększenie obrazu pokazałoby drobniejsze szczegóły.
P = Pob x Pok (0,25 x l) / (fob x fok)
Pob , Pok Powiększenie obiektywu i okularu
l Długość tubusa w metrach
fob , fok. ogniskowe obiektywu i okularu w metrach
To założenia teoretyczne, gdyż rozwój techniczny daje pewną maksymalną możliwą do osiągnięcia zdolność rozdzielczą - max stosuje się powiększenie 1500x (wystarczające do obserwacji najdrobniejszych struktur)
Powiększenie użyteczne (optymalne)
Puż = 1000A
A = apertura numeryczna danego obiektywu
A = n sin u
tg u = m/2h
m 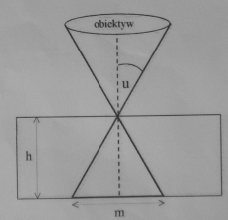
szerokość pola widzenia
h grubość krążka pomiarowego (przypomnieć sobie ćwiczenia)
W praktyce nie warto stosować większych powiększeń od powiększenia użytecznego - nie pozwalają one dostrzec drobniejszych szczegółów danego preparatu.
177.WARUNEK ABBEGO DZIAŁANIA MIKROSKOPU. RÓWNANIE ABBEGO.
„Przez mikroskop dostrzeżemy tylko te szczegóły preparatu, które ugięły światło w takim stopniu, że co najmniej wiązka ugięta I rzędu weszła do obiektywu.”
Jeżeli potraktujemy preparat jako szereg nałożonych na siebie w sposób nieuporządkowany siatek dyfrakcyjnych o różnej stałej, po rozłożeniu go i obserwowaniu każdej siatki oddzielnie przez mikroskop zobaczymy, że poniżej pewnej wartości stałej siatki rysy są niewidoczne. Siatka graniczna, której rysy byłyby jeszcze widoczne to taka, której światło ugięte tworzące prążek I rzędu jeszcze weszło do mikroskopu. Rysy pozostałych siatek, które uginają światło tak silnie, że w mikroskopie powstaje tylko prążek zerowy widma dyfrakcyjnego nie są przez mikroskop rozdzielane. Rzeczywisty obraz światła powstaje na skutek interferencji między wiązkami światła ugiętymi i nieugiętymi.
Można udowodnić, że graniczna siatka dyfrakcyjna tj. ta, której rysy mikroskop jeszcze rozdzieli, miałaby stałą a, dla której słuszny jest wzór określający zdolność rozdzielczą mikroskopu:
d=1a=2Aλ=2 n sinuλ
d- zdolność rozdzielcza mikroskopu
λ- długość fali
n- współczynnik załamania
WNIOSKI:
178.MIKROSKOP ELEKTRONOWY
Według de Brogli`a każda cząstka materialna będąca w ruchu może być rozpatrywana jako fala o długości
. Wiązka pędzących elektronów zachowuje się w polu elektrycznym lub magnetycznym(o symetrii osiowej) podobnie jak wiązka światła w soczewce (bieg elektronów w symetrycznej soczewce elektrostatycznej w Pilawskim str. 285) Dla uzyskania odpowiednich długości fali elektrony przyspiesza się w polu elektrycznym. Próbka znajduje się w próżni i jest często pokryta warstwą metalu. Wiązka elektronów przemiata badany obiekt i trafia do detektorów. Na podstawie sygnałów i badanej próbki urządzenia elektroniczne odtwarzają powiększony obraz. Współczesne mikroskopy osiągają powiększenie rzędu miliona razy i zdolność rozdzielczą około tysiąc razy większą niż w mikroskopach świetlnych (dop=2*109 1/m del=2*1012 1/m)
Preparaty nie muszą być barwione i utrwalane w taki sposób jak do obserwacji w tradycyjnym mikroskopie, dzięki czemu zachowują swoją strukturę, powstający obraz nie jest zniekształcony.
179.Porównanie mikroskopu elektrycznego z optycznym:
Oraz:
1. W mikroskopie optycznym wykorzystuje się promienie świetlne, w mikroskopie elektronowym wiązkę elektronów. W optycznym rolę soczewek spełniają zwykłe soczewki z różnych gatunków szkła, natomiast taką rolę w elektronowym spełniają cewki elektromagnetyczne. W mikroskopie optycznym mamy możliwość obserwacji żywych komórek a w elektronowym martwych gdyż preparat znajduje się w próżni.
2. W mikroskopie optycznym za obiektywem mamy obraz powiększony, odwrócony rzeczywisty (zwany również obrazem pośrednim) a za okularem powiększony, odwrócony pozorny (powiększony względem obrazu pośredniego). W mikroskopie elektronowym uzyskujemy obraz powiększony na ekranie. Jeśli jest to mikroskop transmisyjny mamy zwykły obraz podobny do tego, który widzimy w optycznym (przekrój) a w skaningowym obraz trójwymiarowy. Na jakość oglądanego obrazu wpływa również zdolność rozdzielcza. W mikroskopie optycznym uzyskujemy powiększenia ok. 1000 razy a w mikroskopie elektronowym do milionów razy .
3. W mikroskopie optycznym można zobaczyć pojedyńcze komórki roślinne, zwierzęce, bo wybarwieniu nawet bakterie (pod immersją). W mikroskopie elektronowym możemy zobaczyć struktury komórkowe dokładniej niż w mikroskopie optycznym (struktury komórkowe bakterii w mikroskopie optycznym są niewidoczne a innych komórek niedokładne - zbyt małe aby zobaczyć ich szczególy).
180.Mikroskop z kontrastem fazowym:
Zbudował go Zernick, jego działanie polega na tym, że trzeb spowodować przesunięcie fazy światła nieugiętego o kąt 90stopni, oraz odpowiednio osłabić natężenie tego światła. Wówczas obraz rzeczywisty utworzony przez obiektyw mikroskopu w wyniku interferencji światła nieugiętego, zmiany jasności spowodowane różnicami faz wywołanymi przez preparat będą porównywalne z całkowitą jasnością obrazu. Będą te zmiany rejestrowane przez receptor czuły na różnice energii.
181.MECHANIZM WENTYLACJI PŁUC - prawa
Ruchy powietrza do i z puc spowodowany jest zmienną różnicą ciśnień między powietrzem atmosferycznym a płucami.
WDECH. - podczas wdechu mięśnie oddechowe powiększają objętość klatki piersiowej. Ciśnienie wewnątrzopłucnowe zmniejsza się , a płuca rozciągają się jeszcze bardziej. Wzrost objętości płuc powoduje wzrost objętości pęcherzyków. Zgodnie z prawem Boyle'a - Mariotte'a ze wzrostem objętości gazu zmniejsza się jego ciśnienie. Ciśnienie pp w pęcherzykach staje się nieco mniejsze od ciśnienia atmosferycznego. W ten sposób powstaje spadek ciśnienia w drogach oddechowych wymuszający przepływ powietrza do pęcherzyków. W miarę zwiększania się spadku ciśnienia rośnie strumień powietrza, stając się maksymalny gdy ciśnienie w pęcherzykach osiągnie ok. - 0,2 kPa. Od tej pory tłoczące się do pęcherzyków powietrz e zwiększa panujące w nich ciśnienie, niwelując spadek ciśnienia w drogach oddechowych aż do momentu kiedy ciśnienie sródpęcherzykowe zrówna się z atmosferycznym.
WYDECH. - podczas spokojnego wydechu mięśnie oddechowe rozluźniają się, klatka piersiowa zmniejsza objętość, a siły sprężyste zmniejszają objętość pęcherzyków. Ciśnienie wewnątrzopłucnowe rośnie, a śródpęcherzykowe staje się dodatnie, czyli większe od atmosferycznego. Wzrastające ciśnienie w pęcherzykach wypiera z nich powietrze , jego strumień staje się największy gdy ciśnienie sródpęcherzykowe wzrośnie do ok. 0,02 kPa, po czym maleje aż do momentu kiedy ciśnienie w pęcherzykach ponownie zrówna się z ciśnieniem atmosferycznym.
(wykresy obrazujące wentylacje płuc : Jaroszyk str.595 lub Pilawski str. 313)
182. Surfaktant, rola
Surfaktant to substancja powierzchniowo czynna, zbudowana ze związków lipoproteidowych pokrywająca ściany pęcherzyków płucnych. Zapewnia ciągłą - bez zmian skokowych - zmianę objętości płuc. Napięcie powierzchniowe surfaktantu zależy od grubości jego warstwy:
grubsza warstwa - mniejsze napięcie powierzchniowe ( od 0,510-2 do 110-2 N/m )
cienka warstwa - większe napięcie powierzchniowe
Gdy wdychamy powierzchnia pęcherzyków płucnych zwiększa się, powodując zmniejszenie warstwy surfaktantu. Jako że cieńsza warstwa surfaktantu powoduje zwiększenie napięcia powierzchniowego, to zgodnie z prawem Laplace'a wzrasta ciśnienie. Ów wzrost ciśnienia (wraz z ciśnieniem sprężystym tkanki płucnej) pozwala na utrzymanie równowagi z ciśnieniem napierającego powietrza, dzięki czemu wzrost objętości odbywa się w sposób ciągły, bez zmian skokowych. Przy wydechu mamy do czynienia z odwrotną sytuacją.
Przy braku surfaktantów (co zdarza się głównie u noworodków - wcześniaków) pęcherzyki płucne są zapadnięte, więc wdech wymaga dużego wysiłku do ich otwarcia. Przy wydechu zapadają się one ponownie.
183. Histereza objętościowo-ciśnieniowa płuc
Jest to zjawisko podczas którego inaczej zmienia się objętość płuc przy podwyższaniu ciśnienia niż przy jego obniżaniu. Podczas badania właściwości mechanicznych tkanki płucnej, wyizolowane płuca nadmuchuje się powietrzem (inflacja) mierząc ciśnienie i objętość, a następnie opróżnia (deflacja) wykonując identyczne pomiary. Wyniki pomiarów przedstawione na wykresie świadczą o tym, że inaczej zmienia się objętość płuc przy podwyższaniu ciśnienia niż przy jego obniżaniu - jest to zjawisko histerezy objętościowo-ciśnieniowej. Przyczynami tego zjawiska są:
właściwości sprężyste tkanki płucnej
napięcie powierzchniowe warstwy powierzchownej pęcherzyków płucnych
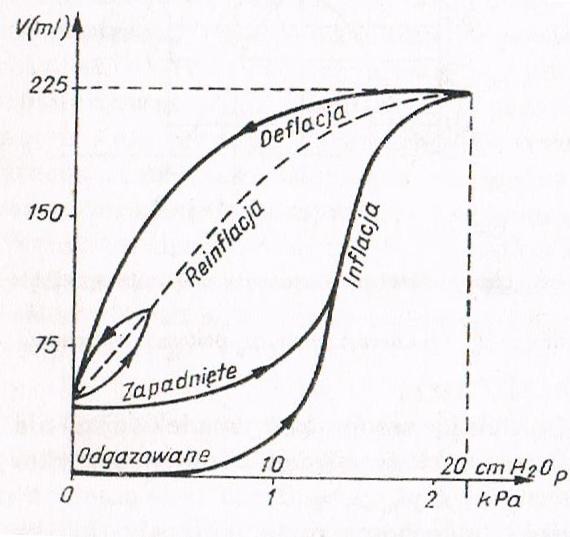
Analizując wykres możemy wyróżnić:
1. Proces inflacji (wdechu) - 3 fazy
2. Proces deflacji (wydechu) - 2 fazy
184. Rola właściwości sprężystych tkanki płucnej, napięcia powierzchniowego warstwy powierzchniowo - pęcherzykowej i promienia pęcherzyków płucnych w mechanice oddychania.
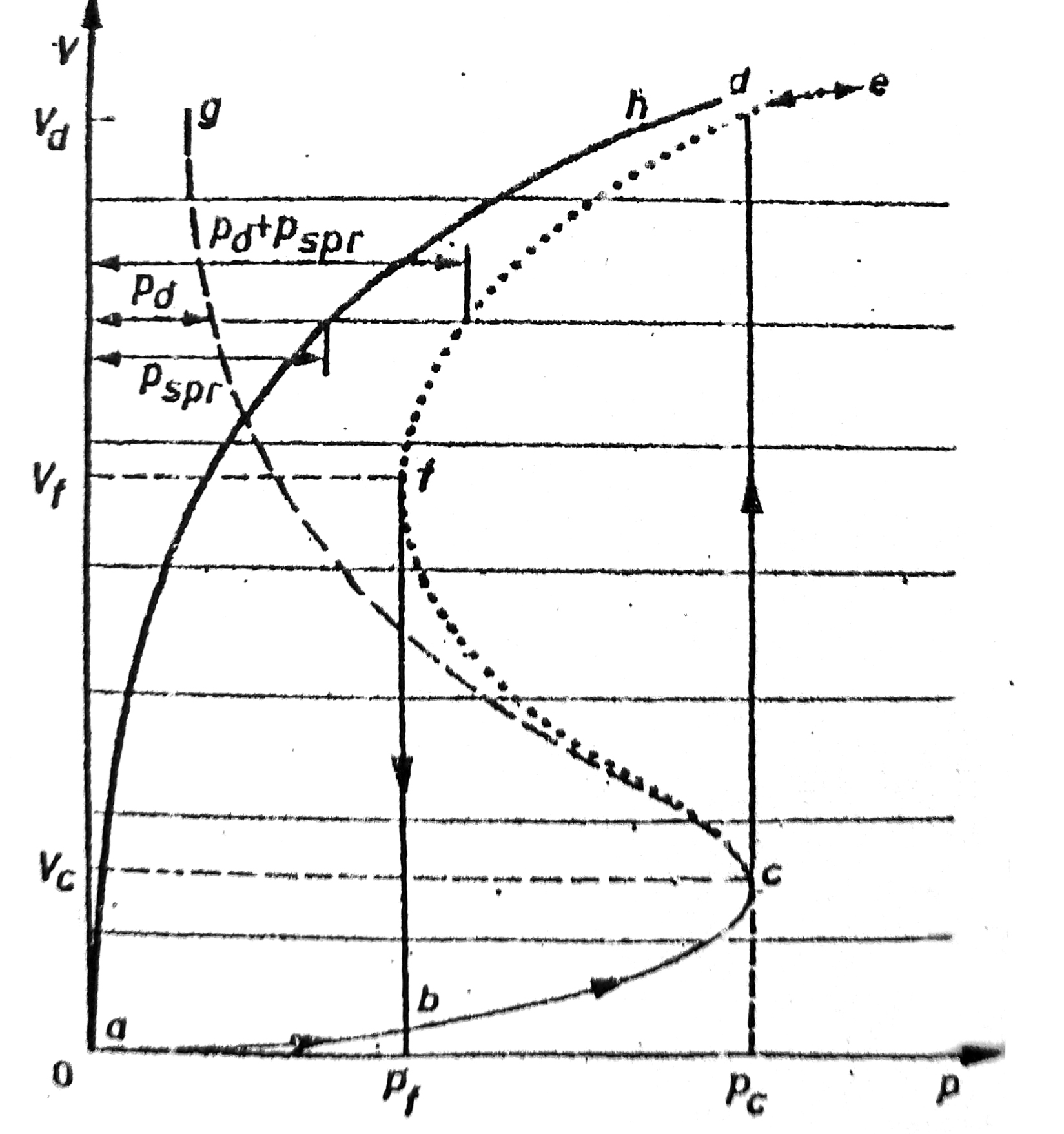
Opory sprężyste, do których zaliczamy napięcie powierzchniowe i sprężyste napięcie tkanki pęcherzyków płucnych sprawiają, że płuca wykazują stałą skłonność do biernego zapadania się podczas ich rozciągania. W wyniku działania sił napięcia powirzchniowego wytwarza się w pęcherzyku ciśnienie, które jest tym większe, im mniejszy jest promień pęcherzyka. Zależność tą wyraża prawo Laplace'a:
.
Gdyby zobrazować zjawisko na modelu dwóch baniek połączonych rurką, to powietrze będzie przepływało z bańki o promieniu mniejszym do bańki o promieniu większym. Taka sytuacja uniemomżliwiałaby oddychanie, jednak częsciowo układ pęcherzyków jest stabilizowany przez siły sprężyste, spowodowane obecnością włókien sprężystych i kolagenowych tkanki łącznej. Dzięki temu po przekroczeniu pewnej objętości Vc pęcherzyki skokowo przyjmują objętość Vd gdzie siły napięcia powierzchniowego zostają zastąpione przez siły sprężyste i bańka nie pęka (wykres).
Krzywa ah - zależność objętości V od ciśnienia psp ,
za które odpowiedzialne są siły sprężystości
Krzywa abcg - zależność objętości V od ciśnienia pσ,
Za które odpowiedzialne jest napięcie powierzchniowe
Krzywa abcfd - krzywa wypadkowa
185.Praca i moc układu oddechowego, graficzny sposób wyznaczania pracy ukł.oddechowego, wzory, interpretacja.
Na prace wykonywaną przez układ oddechowy składa się ruch klatki piersiowej, przepony, niektorych narządów śródpiersia i jamy brzusznej, płuc oraz powietrza.
Obliczenia teoretyczne ograniczają sie tylko do pracy wykonywanej na uruchomienie samych płuc i powietrza. (reszta trudna do ujęcia matematycznego)
Wzrost objętości płuc podczas wdechu dokonuje się za pośrednictwem różnicy ciśnień jaka istnieje miedzy pęcherzykami a opłucna.
Zwiększając objętość płuc o dV przy ciśnieniu p zostaje wykonana praca dW=pdV
pracę wykonaną przy zwiększeniu objętości płuc o objętość oddechową V(t) należy obliczyć za pomocą całki:
W=~ pDV
obliczenie tej całki wymaga znajomości funkcji p=f(V)
Na ciśnienie p składa się: p=Psp+ Ppow+ Pl+ Pm
Psp- cieśninie pokonujące opory sprężyste tkanki płucnej
Ppow- ciśnienie pokonujące opory ruchu powietrza w drogach oddechowych
Pl-ciśnienie pokonujące opory lepkościowe
pm- pokonanie oporów bezwładności mas wprowadzanych w ruch (możemy pominąć)
p=psp+pnp pnp-opory nie sprężyste czyli ppow i pl
więc prace możemy wyrazić jako praca wykonana przeciw siła sprężystym oraz niesprężystym:
W=~Psp dV + ~Pnp dV
Praktycznie prace można wyznaczyć metodą planimetryczną(przez pomiar pola)
W tym celu rejestruje się przy oddychaniu ciśnienie wewnątrzopłucnowe za pomocą urządzenia urządzenia manometrycznego połączonego z igła wkłutą do przestrzeni opłucnowej.
Rys 14.6 PIlawski str 319
krzywa ABC-wdech, CEA-wydech
Pętla ABCEA przedstawia histerezę dynamiczną, otrzymaną w czasie ruchu płuc i powietrza.
można wykazać ze pole trapezu ACDO wyraża pracę wykonaną przeciw oporom sprężystym podczas wdechu(pierwsza cześć całki) a pole ABCA odpowiada oporom niesprężystym.
siły sprężyste podlegają prawu hooka'e czyli: przyrost ciśnienia jest proporcjonalny do przyrostu objętości
dp=1/C* dV
wpołczynnik c=dV/dp to podatność płuc wyraza ona liczbowo zmianę objętości płuc wywołaną jednostkową zmianą ciśnienia sprężystego
więc całka przyjmuje dla oporów sprężystych: Wsp= ~(po+1/C *V)dV
Z pomiarów pola trapezu OACD otrzymuje się prace wykonaną przeciw oporom sprężystym płuc, wynosi ona 0,3J na wdech. Na pokonanie oporów niesprężystych wypada ok 0,1J na wdech i tyle tez na wydech.
Cała praca uruchamiająca płuca i powietrze wynosi więc ok 0,5J na jeden cykl trwający ok 4s. (8l/min) to moc zużyta przez mięśnie oddechowe na ten cel wynosi ok 0,13W.(wynika to oczywiście ze wzoru na moc czyli P=W/t)
186. Praktyczna metoda obliczania pracy w układzie oddechowym:
Pracę wykonaną przez mięśnie oddechowe podczas oddychania można obliczyć na podstawie wydatku energetycznego przeznaczonego na ten cel, który wyraża się tzw. kosztem tlenowym. Mierzy się w tym celu nadwyżkę tlenu zużytego ponad poziom oddychania w spoczynku przy oddychaniu wysiłkowym. Z otrzymanych danych można wyliczyć zużycie tlenu na spokojne oddychanie. Przy wentylacji 8 l/min zużycie tlenu wynosi około 4×10-3 l O2/min. Uwzględniając współczynnik energetyczny tlenu, który wynosi 20 kJ/l , otrzymuje się energię zużytą na oddychanie - 80 J/min. Odpowiada to mocy 1,4 W. Stanowi to niecałe 2% przemiany spoczynkowej.
187. Rodzaje oporów sprężystych:
?(nie z książki)
Opór sprężysty- to głównie sprężysty opór klatki piersiowej i siły retrakcji płuc- tzn. siły wywołującej tendencje ścian pęcherzyków płucnych do zapadania się; jest to głównie napięcie sprężyste pęcherzyków płucnych i napięcie powierzchniowe.
188. Biofizyczne mechanizmy i prawa dotyczace wymiany gazowej miedzy krwia a pecherzykami plucnymi, wzory i interpretacja.
Wymiana gazów oddechowych odbywa się na drodze dyfuzji. Zasadniczą rolę w tym procesie odgrywa rozpuszczalność gazów we krwi. Rozpuszczalność gazów w cieczy podlega prawu Henry'ego.
„Stężenie gazu rozpuszczonego w cieczy jest w stanie równowagi proporcjonalnie do ciśnienia cząstkowego (p) gazu pozostałego nad cieczą, niezależnie od obecności innych gazów.”
Prawo to można wyrazić wzorem;
c = α
gdzie; c - stężenie gazu w cieczy,wyraża się najczęściej stosunkiem objętości Vg jaką gaz rozpuszczony zajmowałby w warunkach normalnych, do objętości V cieczy.
α - współczynnik rozpuszczalności gazu , zwany też współczynnkiem absorpcji. Zależy od rodzaju gazu i cieczy, od temperatury(maleje ze wzrostem temperatury) oraz ciśnienia całkowitego gazów nad cieczą.[ α=
]
p - ciśnienie cząstkowe danego gazu nad cieczą.
Jako miarę ilości gazu rozpuszczonego w cieczy podaje się ciśnienie cząstkowe tego gazu w warunkach równowagi przy p = const. i T =const.
Podczas wdechu do płuc dostaje się ok. 0,5 l powietrza, z tego 0,12 l pozostaje w przestrzeni martwej (drogach oddechowych). Reszta miesza się z powietrzem w przestrzeni czynnościowej zalegającej płuca. Skład powietrza w pęcherzykach różni się w związku z tym od składu powietrza atmosferycznego.
Także powietrze wydechowe zmienia skład w stosunku do pęcherzykowego, miesza się bowiem onoz powietrzem w przestrzeni martwej, zmniejsza się stężenie CO2, a zwiększa O2.
Ciśnienie cząstkowe pary wodnej nie zmienia się w płucach i krwi, gdyżjest to para nasycona, której prężność od ojętości nie zależy.
Porównanie ciśnień cząstkowych gazów oddechowych w powietrzu atmosferycznym, płucach i krwi pozwala uzasadnić kierunek dyfuzji tych gazów.
Szybkość dyfuzji gazów z pęcherzyków do krwi wyraża się strumieniem objętości dV/dt gazu dyfundującego poprzez błony pęcherzyków i ściany naczyń do krwi. Strumień objętości dyfundującego gazu jest proporcjonalny do różnicy ciśnień cząstkowych gazu w pęcherzykach
i w naczyniach włosowatych
, czyli :
=
(
-
)
Współczynnik proporcjonalności
nazywa się zdolnością dyfuzyjną płuc. Wyraża objętość gazu dyfundującą w jednostce czasu przy jednostkowej różnicy ciśnień cząstkowych gazu między pęcherzykami a krwią. Zależy od; właściwości błon, powierzchni, rozpuszczalności gazu. Wpływana niego różnica ciśnień cząstkowych gazu między pęcherzykami a krwią - krew zabierając tlen nie dopuszcza do wyrównania ciśnień.
189.Dynamiczne rozproszenie światła
W rzeczywistych strukturach-cząsteczki lub ich związki-wykonują chaotyczne ruchy termiczne - zwane ruchami Browna, przemieszczając się względem określonego układu odniesienia. Stąd na skutek zjawiska Dopplera następuje poszerzenie częstotliwości światła rozproszonego w stosunku do częstotliwości światła padajacego. Ten rodzaj rozproszenia nazywamy DYNAMICZNYM ROZPROSZENIEM ŚWIATŁA. Wyjaśnienie tego zjawiska oparte jest na zjawisku fluktuacji lokalnych (wyjaśnienie podali niezależnie Smoluchowski i Einstein). Obecnie wykorzystuje się metodę DLS oraz odpowiednie teorie hydrodynamiczne do określenia rozmiarów i kształtu związków wielkocząsteczkowych.
[Ilustracja graficzna zmiany częstotliwości świtała w rozpraszaniu dynamicznym- F. Jaroszyk str. 73]
190.Rozproszenie Ramana
(zjawisko Ramana, rozpraszanie kombinacyjne, rozpraszanie ramanowskie)
WYJAŚNIENIE ZJAWISKA Rozproszenie to zachodzi w ciałach stałych, ciekłych i gazowych. Światło rozproszone zawiera poza długością fali światła padającego λ0 także fale nieco dłuższe λ0+ Δλ i krótsze λ0 - Δλ .Zjawisko polega na tym, że światło o energii fotonów hvo powoduje wzbudzenie cząstek substancji, przez którą przechodzi. Cząsteczka ze stanu o energii Ej przechodzi do stanu El=Ej+hv0 [Rys. Jaroszyk s.72]. Przy powrocie do stanu wyjściowego Ej zostaje wypromieniowany foton o tej samej hv0. Jeżeli jednak cząsteczka zamiast do stanu Ej przejdzie do stanu o energii Ek nieco większej, zostanie wypromieniowany foton o nieco mniejszej energii El-Ek= h(v0- Δv) przy czym energia hΔv odpowiada wzbudzonym poziomom oscylacyjnym lub rotacyjnym. W świetle rozproszonym znajduje się wówczas obok linii widmowych o częstotliwości podstawowej v0 także linia o częstotliwości v=v0- Δv, o nieco dłuższej fali (rozproszenie ramanowskie) Istnieje też możliwość, że foton, trafiając na cząsteczkę, zastanie ją w stanie energii Ek; cząsteczka absorbując go, przechodzi w stan pobudzony El. Przy przejściu do stanu wyjściowego Ej zostanie wypromieniowany kwant o energii większej hv=hv0+hΔv. W tym przypadku w widmie światła rozproszonego pojawia się linia o częstotliwości większej (czyli o fali krótszej). Linia ta nazywa się linią antystokesowską, ma natężenie mniejsze: prawdopodobieństwo takiego zdarzenia jest mniejsze.
ZASTOSOWANIE Efekt Ramana wykorzystuje się w analizie materiałowej i spektroskopii. Stosunek intensywności pasm stokesowskich i antystokesowskich może posłużyć do wyznaczenia temperatury obiektu rozpraszającego.
W SKRÓCIE
Polega ono na tym, że przy rozproszeniu wiązki światła w widmie rozproszonym występują, obok fotonów o takiej samej energii (rozpraszanie Rayleigha) fotony o zmienionej energii. Powoduje to powstanie w widmie, obok pasma Rayleigha o takiej samej częstotliwości jak światło padające, tak zwanych pasm stokesowskich i antystokesowskich o odpowiednio zwiększonej i zmniejszonej częstotliwości, symetrycznie położonych po obu stronach pasma Rayleigha.
191.Rozproszenie światła Tyndalla
Efekt Tyndalla-jest to zjawisko rozproszenia światła przez roztwory koloidowe(roztwory makrocząsteczek)
[Jeżeli przez roztwór koloidalny przepuści się wiązkę światła, to wskutek uginania się promieni na cząstkach fazy rozproszonej, światło staje się widoczne w postaci tzw. stożka Tyndalla. Intensywność tego zjawiska jest tym większa, im większa jest różnica między współczynnikiem załamania fazy rozproszonej i ośrodka dyspersyjnego. Z wikipedii;)]
Natężenie światła I przechodzące przez warstwę roztworu o grubości l jest mniejsze od natężenia światła padającego I0
I=I0 e-τl
τ-współczynnik rozpraszania światła,zależy on od różnicy współczynników załamania światła substancji makrocząsteczkowej i rozpuszczalnika (n-n0), od masy cząsteczkowej M, stężenia roztworu c i długościfali świetlnej λ
Rozproszenie światła przez makrocząsteczkę na ryc 8.13. Pilawski str. 190
Makrocząsteczka jest tu potraktowana jako punkt rozpraszający światło.
Dla cząsteczek o wymiarach porównywalnych z długością fali świetlnej należy uwzględnić interferencje promieni rozproszonych od różnych punktów tej samej makrocząsteczki(ryc.8.14. Pilawski str.190)Natężenie światła rozproszonego zależy od kąta pod którym prowadzimy obserwację.
192.Rozproszenie światła Rayleigha
Rozpraszanie może być spowodowane przez atomy, cząsteczki, jony lub zawiesiny.
W rozproszeniu Rayleigha nie zmienia się długość fali.Zderzenia fotonów z „ośrodkami” rozproszenia są sprężyste. W rozpraszaniu rayleighowskim światła zakłada się, że czasteczki, w których następuje indukowanie dipoli elektrycznych emitujących wtórną falę elektromagnetyczną o niezmienionej częstotliwości, są nieruchome. Rysunek 4.12 w Jaroszyku na str.71
193 Rozpraszanie światła w roztworach koloidalnych
Efekt Tyndalla to zjawisko fizyczne polegające na rozpraszaniu światła przez koloid z
wytworzeniem charakterystycznego stożka świetlnego nazwanego efektem (zjawiskiem)
Tyndalla.
Jeżeli przez roztwór koloidalny przepuści się wiązkę światła, to wskutek uginania się
promieni na cząstkach fazy rozproszonej, światło staje się widoczne w postaci tzw. stożka
Tyndalla. Intensywność tego zjawiska jest tym większa, im większa jest różnica między
współczynnikiem załamania fazy rozproszonej i ośrodka dyspersyjnego.
W przypadku wymiarów cząstek znacznie mniejszych od długości fali promieniowania
rozpraszanego λ, natężenie światła rozproszonego IΘ pod kątem Θ do kierunku światła
padającego I0, mierzone w odległości R od rozpraszającej objętości V, wyraża się wzorem:
IΘ = I0·(8π4NVα2/λ4R2)·(1+cos2Θ),
gdzie:
N - liczba cząsteczek rozpraszających w jednostce objętości,
α - polaryzowalność cząstek rozpraszających, zależna od współczynników załamania światła
dla układu koloidalnego i czystego rozpuszczalnika.
Najsilniej ulega rozproszeniu światło o najkrótszej fali, co stanowi przyczynę błękitnej barwy
nieba (rozproszenie światła na cząstkach atmosferycznych) oraz dymu papierosowego.
197 Chromatografia żelowa
Chromatografia żelowa (sączenie żelowe) jest to metoda stosowana jest do rozdziału głównie białek i wielocukrów ze względu na różnice w ich wielkości i kształcie.
Kolumnę chromatograficzną wypełnia się złożem (faza stacjonarna) w postaci ziarenek o określonej wielkości porów zbudowanych z nierozpuszczalnego polimeru (typu: dekstran, agaroza) lub poliakrylamidu.Po nałożeniu na żel mieszaniny, białka o małych rozmiarach wnikają do wnętrza ziaren duże natomiast nie mogą. Droga do momentu wycieku z kolumny, którą musi pokonać każdy ze składników próbki jest więc nierówna. Cząsteczki o najmniejszym ciężarze cząsteczkowym mają do pokonania najdłuższą drogę i dlatego wypływają najpóźniej z kolumny. Białka o dużej masie cząsteczkowej i o średnicy większej niż pory ziaren złoża mają do pokonania krótszą drogę w żelu i wędrują najszybciej. Pojawiają się zatem jako pierwsze u wylotu kolumny.
198 Dyfuzja makrocząsteczek w roztworze, współczynnik dyfuzji a geometria makrocząsteczek, wzór, rola, przykładowe wartości
Współczynnik dyfuzji D zależy m.in. od rozmiarów i kształtów cząsteczek dyfundujących, tak więc pomiar tego współczynnika może dostarczyć informacji o cechach makrocząsteczek.
Dla cząsteczek kulistych zależność współczynnika D od promienia cząsteczki wyraża wzór:
gdzie: n- lepkość rozpuszczalnika r- promień cząsteczki
k- stała Boltzamana D- współ. Dyfuzji (cm2/s)
T- temperatura
Współczynnik dyfuzji zgodnie ze wzorem jest odwrotenie proporcjonalny do wartości promienia r.
Dzieje się tak ze względu na wytstępujące siły tarcia w roztworach.
Współczynnik ten może się przydać do wyliczenia masy cząsteczkowej (gdy są znane także dane o sedymentacji w ultrawirówce)
-11
Przykładowe wartości: 10 m2/s dla białek a dla substancji małocząsteczkowych ok 10-100 razy większy.
199 I zasada termodynamiki
Przyrost energi wewnętrznej U2-U1 układu jest równy sumie dostarczonego mu ciepła Q i wykonanej pracy, co wyraża się wzorem:
U2-U1=Q+W
Ewentualnie:1. Energia wewnętrzna U układu jest energią związaną z nieuporządkowanym ruchem cząsteczek, zarówno kinetyczną jak i potencjalną ich wzajemnego oddziaływania.
2. Wzór wyżej podany można przestawić w formie (-W)+( U2-U1)=Q wtedy można powiedzieć że ciepło dostarczone układowi zużywa się na wzrost jego energi wewnętrznej i wykonaną przez układ pracę.
Przy dostarczaniu układowi ciepła przyrost energi wewnętrznej zależy od tego czy układ wykonuje pracę. Np: przy ogrzewaniu gazu przy stałej objętości praca nie jest wykonywana W=0 (bo -W=pΔV a zmiana objętości ΔV=0) więc całe ciaepło jest wykorzystywane na wzrost energi wewnętrznej Q=( U2-U1). Gdy jednak układ zmienia objętość to -W=pV a więc Q=( U2-U1)+pΔV
200 - I zasada terodynamiki w układach biologicznych, biokalorymetria pośrednia i bezpośrednia
I zasada termodynamiki jako zasada zachowania energi powinna być zachowana w procesach biologicznych. Energia organizmowi jest potrzeban do zachowania struktury, przeprowadzanai procesów, wykonywania czynności. Pochodzi ona z utleniania produktów pokarmowych przy stałej temperaturze i ciśnieniu. Energia odstarczona nie jest jednak równa entalpi swobodniej ΔG gdyż część energi (76kJ/mol glukozy) wchodzi w skład energi związanej i proces ten nie jest odwracalny. Dlatego za miarę energi dostarczonej przyjmuje się entalpie ΔH.
Kosztem energi ΔH organizm wykonuje pracę wewnętrzną Wi i zewnętrzną We. Praca zewnętrzna jest równa pracy wykonanej kosztem wysiłku mięśniowego. Praca wewnętrzna związana jest z pokonywaniem oporów podczas wielu procesów (krążenie, oddychanie, transport przeciw gradientom stężeń itp) i w końcowym efekcie zamienia się w ciepło Wi=Q.
Bilans Energi wyraża się więc wzorem ΔH= We+Q
Ciepło oddawane przez organizm do otoczenia można mierzyć dzięki kalorymetrom.
1. Biokalorymetria bezpośrednia - obiekt badany znajduje sięw komorze o dokładnej izolacji cieplnej. Ilość ciepła wytworzoną w komorze mierzy się ilością ciepła pobraną przez wodę przepływającą przez system rur znajdujący się w komorze.
Mierząc masę m przepływającej wody i przyrost jej temperatury ΔT ilość ciepła obliczymy ze wzoru: Q=cmΔT.
Wielkość wykonanej pracy We mierzy się za pomocą cykloergometru (przypomina rower)
Energię którą organizm otrzymuje, mierzy się energią którą organizm pobrał w procesach utleniania związków pokarmowych (przydatne tabele wykorzystania energi przez organizm z utlenienia danego związku)
Kalorymetr ten pozwala także zmieżyć ilość zużytego przez organizm tlenu i wydalonego CO2, a wiedząc ile tlenu się zużywa na spalenie określonej ilość związku i ile względnie powinno w tym procesie powstać CO2 można obliczyć ciepło metabolizmu.
2. Kalorymetria pośrednia - polega na pomiarze ilości pobranego tlenu i wydalonego CO2, wykorzystuje siędo tego maskę/ustnik oddzielający powietrze wydychane i wdychane. Obliczenie ciepła metabolizmu wymaga jednak znajomości jaki składniki został utleniony. Określić to pomaga iloraz oddechowy RQ, wyraża się on stosunkiem objętości wydalonego przez organizm dwutlenku węgla Vco2 do objętości pobranego tlenu Vo2 : RQ= Vco2 /Vo2
Stosunek oddechowy dla węglowodanów wynosi 1 dla tłuszczów 0,71 a białek 0,81
Pomiary kalorymetryczne pozwalają zmierzyć:
201. II zasada Termodynamiki
Za wielkość określającą stan uporządkowania układu można przyjąć wprowadzoną przez Boltzmanna wielkość S proporcjonalną do ln W (liczba mikrostanów wyrażająca liczbe sposobów wg. Ktorych z elementow mikroskopwych daje sie zrealizowac dany stan makroskopowy układu)
Więc:
S=k*lnW
Gdzie: k - stała Bolzmanna
S- jest funkją stanu zwaną jako entropia
Entropia jest funkcją stanu określającą w jakim kierunku mogą zachodzić procesy w układnie izolowanym.
Jeżeli entropia początkowo była S1= k lnW1 a końcowo S2= k lnW2 to przy przejsciu ze stanu 1 do stanu 2 entropia układu zmieni się o
ΔS= S2-S1 = k ln W2/W1=k ln P2/P1
W układzie izolowanym proces zmierza w kierunku od mniejszego prawdopodobieństwa P1 do większego P2, od Mniejszego nieporządku W1 do większego W2..
Wobec tego P2>P1 oraz W2>W1 . Musi być:
S2 > S1
ΔS > 0
W układzie izolowanym procesy mogą zachodzić tylko w kierunku wzrostu Entropii ; w stanie równowagi entropia przyjmuje wartość stałą maksymalną.
ΔS=0 S=Smaks -> w stanie równowagi
Jest to treść drugiej zasady termodynamiki
Clausjusza.
Wg Clausjusza doprowadzenie do układu ciepła w ilości dQ przy temp. T w sposób quasi-statyczny powoduje wzrost entropii układu o
dS =
proces quasi-statyczny
Jeżeli temp układu zmieni sie podczas dostarczania ciepła zmiana entropii ΔS układu wyrazi sie wzorem
ΔS = S2-S1 =
Poglądowo interpretacja wygląda tak: Dodanie ciepła w ilości dQ oznacza dodanie nieporządku co powoduje wzrost entropii. W im wiekszej temp to zachodzi tnz. Przy im wiekszym stanie nieporządku dodamy go jeszcze troche tym mniejsze to powinno miec znaczenie dla entropii, czego odpowiednikiem jest T w mianowniku . Dotyczy to procesow odwracalnych
Nieodwracalne psuja porządek na wlasna reke przyrost entropii jest wiec wiekszy od tego spowodowanego odwracalnym dodaniem ciepła dQ. Czyli:
dS =
lub dS = dSe + dSi
Na przyrost entropii składa sie : przyrost dSe wynikający z dodania ciepła dQe ; oraz przyrost dSi będący wynikiem procesów nieodwracalnych. Ciepło dQi zwane jest ciepłem nieskompensowanym - wytworzone w procesach dyssypacyjnych, rozpraszajacych energie w wyniku pokonywania oporow np tarcia.
Zawsze jest dSi = dQi / T > 0
Wyrazenie dS =
lub dS = dSe + dSi mozna uznac za ogólne sformułowanie drugiej zasady termodynamiki .
Układ izolowany dQe = 0
Proces quasi statyczny dSi = 0 Proces nieodwracalny dSi > 0
dS=0 S=const dS>0 S2>S1
W układzie izolowanym entropia nie może maleć dS ≥ 0
Wymieniajacy ciepło z otoczeniem dQe ≠ 0
Proces q s : dSi = 0 Proces nieodwracalny dSi > 0
dS =
dS >
W układach wymieniajacych ciepło z otoczeniem przyrost entropii dS nie moze byc mniejszy od
dS ≥
202 II zasada w układach biologicznych
Entropia organizmu żywego stanowiącego układ otwarty zmienia sie zgodnie z szybkością
=
gdyby organizm był układem zamknietym po pewnym czasie organizm znalazłby sie w stanie równowagi statycznej rownoważnej ze śmiercią.
Organizm stanowiąc układ otwarty wymienia entropie dSe z otoczeniem ; otrzymuje bowiem entropie
dS'e > 0 z pokarmem oraz oddaje dS''e < 0 wraz z zdegradowanymi produktami przemiany materii i zdegradowana energią ( w postaci ciepła). Wymieniona z otoczeniem entropia dSe jest ujemna :
dSe = |dS'e| - |dS''e| < 0 bowiem |dS'e| < |dS''e| . Rownoczesnie w organizmie zachodzą procesy nieodwracalne tworzace entropie dSi. W organizmie dojrzalym nie zmieniającym biomasy szybkosc tworzenia entropii jest rowna szybkosci oddawania dSi/dt = |dSe /dt|
Entropia organizmu nie zmienia sie w czasie dSorg/dt = 0 , Sorg= const. Organizm znajduje sie w stanie stacjonarnym.:
Model org żywego w stanie stacjonarnym. (jakby co rysunek 6.2 strona 150 Pilawski)
W stanie stacjonarnym stale czynne sa procesy nieodwracalne destrukcyjne tworzące entropie . Procesom tym przeciwstawiaja sie procesy konstruktywne zwiazane z wymiana entropii z otoczeniem zmniejszające entropie.
;Stwierdzono doświadczalnie ze młode organizmy w rozwoju oddaja wiecej ciepła do otoczenia , odznaczają sie większą dyssypacją energii niż organizmy dojrzałe . Znaczy to że w stanie rozwoju żródło entropii jest wieksze od wymaganego zasada Prigogine'a minimum . Swiadczy to o zywiej zachodzacych procesach metabolizmu i o wiekszej aktywnosci organizmu. Mozna zaryzykowac stwierdzenie ze szybkosc produkcji entropii jest miara zywotnosci organizmu. Stąd wniosek ze dla utrzymania wiekszej zywotnosci , dla zachowania mlodosci nalezy zwiekszyc procesy metabolizmu, prowokujace zwiekszenie produkcji entropii, prowokujace zarazem org. Do walki z nia. Uzyskuje sie to przede wszystkim aktywnoscia fizyczna. Wysiłek wzmaga procesy transportu zwiekszajac z jednej strony zrodlo entropii a z drugiej zwiekszajac zapotrzebowanie na energie i materie (pokarmy)
Utrzymanie organizmu przy zyciu okupione jest wzrostem entropii otoczenia . Jesli za układ uwazac organizm i otoczenie bedzie to uklad izolowany. Zgodnie z 2 zasada termodynamiki entropia w takim ukladzie moze tylko rosnac : ΔSprzyrody = ΔSorg + ΔSotoczenia > 0
203. III zasada termodynamiki
Sformulował ją Nernst : dla układów skondensowanych (ciala stałe i ciecze) entropia staje sie zerem w temperaturze zera bezwzględnego .
Postulat ten uogólnił Planck: entropia każdego ciała doskonale jednolitego jest zerem w temp zera bezwzględnego.
Lim S = 0
T->0
Postulat wywodzi sie z zaleznosci S = k lnW
Ciało doskonale jednolite to ciało ktorego uporzadkowanie w zerze bezwzglednym jest doskonale to znaczy że W = 1 czyli S = 0
Wynikaja z tej zasady ważne wnioski np możliwośc obliczenia bezwzględnej wartosci entropii ciał dla ktorych jest spełniona
204. Równania fenomenologiczne
Bodzce wywołują transport odpowiednio: energii, substancji, ładunku elektrycznego. Zjawiska te podlegaja prawom:
prawo fouriera przewodzenia ciepła ( s - powierzcnia
- przewodność cieplna własciwa ,
dT/dx - spadek temperatur)
prawo Ficka dyfuzji
prawo Ohma przewodzenia pradu ( dq/dt -prad elektr,
- przewodnosc elektr wlasciwa,
dV/dx - spadek pot. Elektr)
Oznaczając bodźce termodynamiczne ogolnie przez Xi oraz przyporządkowane im przepływy przez
Ji =
(gestość strumienia odpowiednio : ciepła przy di= dQ, substancji przy di=dn, ładunku elektrycznego przy di = dq)
Prawa te mozna ogólnie ując jednym wzorem Ji = LiXi (Li - wspolczynnik proporcjonalnosci
charakteryzujący dane zjawisko , wyraza
liczbowo przeplyw odpowiadajacy bodzcowi jednostkowemu)
Transport opisany tym wzorem jest raczej uproszczeniem, na ogoł w ukladzie dziala nie jeden a wiecej bodzców wzajemnie od siebie zaleznych. Pojawiają sie wtedy przeplywy wymuszone zwane sprzezonymi powodujac pojawienie sie nowych bodzców. Np bodziec temp w mieszaninie gazów poza transportem energii powoduje wtórnie transport dyfuzyjny - termodyfuzje.
Wtedy kazdy przeplyw Ji jest funkjcą nie tylko bodzca Xi ktoremu jest przyporzadkowany ale tez funkcją pozostalych bodzców.
Ji = f(X1,X2,...,Xi...,Xn)
Przyjmuje sie ze funkcje te są liniowe co jest uzasadnione w stanie niezbyt odleglym od równowagi. Mozna wtedy napisac równania
Ji = Li1X1+ Li2X2...+ LiiXi... LinXn, i=1,2...n
Rownan takich jest n po jednym dla kazdego przepływu J1,...Jn - nazywa sie je równaniami fenomenologicznymi. Wspolczynniki L zwane wspolczynnikami fenomenologicznymi charakteryzują zachodzące procesy transportu. Jest ich n2 . Wg onsagera wspolczynniki symetryczne sa sobie rowne Lik=Lki
Wtedy liczba charakteryzują proces ogranicza sie do ½ (n2+n)
Przy 2 bodzcach np. J1= L11X1+L12X2
J2= L21X1+L22X2 Proces charakteryzuja 3 wspolczynniki L11,L22, L21=L12
PYTANIE 205 ENTROPIA
Entropia- funkcja stanu określająca stan uporządkowania układu, która zgodnie ze wzorem Boltzmanna jest proporcjonalna do lnW, a więc:
S= k*lnW gdzie: k- stała Boltzmanna
W- liczba mikrostanów, wyrażająca liczbę sposobów
według których z elementów mikroskopowych
daje się zrealizować dany stan makroskopowy
układu. Stan makroskopowy gazu jest
opisany parametrami mierzalnymi (ciśnienie
temp) które to wielkości są wynikiem
uśredniania wielkości mikroskopowych (pędy
cząsteczek, ich energie). Miara nieporządku w
stosowana w termodynamice.
Wcześniej entropia została wprowadzona przez Clausjusza na podstawie rozważań Carnota dotyczących sprawności motorów cieplnych.
Entropia określa w jakim kierunku mogą zachodzić procesy w układzie izolowanym. Jeżeli entropia układu w stanie początkowym była S1= k*lnW1 a w stanie końcowym S2=k*lnW2 to przy przejściu ze staniu początkowego do końcowego entropia układu zmieni się o:
ΔS=S2-S1= k*lnW2/W1= k*lnP2/P1
W układzie izolowanym proces zmierza od prawdopodobieństwa mniejszego P1 do prawdopodobieństwa większego P2 czyli od mniejszego nieporządku W1 do większego W2. Skoro więc P2>P1 oraz W2>W1 to:
S2>S1
ΔS>0
W układzie izolowanym procesy mogą zachodzić tylko w kierunku wzrostu entropii. W stanie równowagi entropia przyjmuje wartość stałą maksymalną (II zasada termodynamiki):
ΔS=0 S=Smax (stan równowagi)
PYTANIE 206 ENTROPIA A WYMIANA CIEPŁA
I. Procesy odwracalne
Jeśli doprowadzimy do układu ciepło w ilości dQ przy temperaturze T w sposób quasi-statyczny (odwracalny) to nastąpi wzrost entropii układu o:
dS= dQ/T
Jeżeli temp. układu zmieni się w czasie dostarczania ciepła to zmiana entropii układu wyrazi się wzorem:
T2
ΔS= S2-S1= ƒ dQ/T
T1
Z powyższej zależności wynika, że dodanie ciepła do układu w ilości dQ jest równoznaczne z dodaniem nieporządku (nieuporządkowany ruch cieplny) z czym wiąże się wzrost entropii. Jednak w im wyższej temperaturze proces ten zachodzi tym mniejsze ma to znaczenie dla entropii (świadczy o tym T w mianowniku)
II. Procesy nieodwracalne
W procesach nieodwracalnych przyrost entropii będzie większy od tego, który wby był spowodowany odwracalnym dodaniem ciepła dQ (dyż procesy te „psują” porządek na własną rękę) co wyraża wzór:
dS= dQe/T + dQi/T lub po prostu dS=dSe+dSi
Zatem jak wynika ze wzoru na przyrost entropii układu składa się przyrost dSe wynikąjący z dodania ciepła w ilości dQe oraz przyrost dSi wynikający z procesów nieodwracalnych, w których ciepło dQi (ciepło nieskompensowane) to ciepło wytworzone w procesach dyssypacyjnych, rozpraszających energię w wyniku pokonywania oporów (tarcie, lepkość itp.) Należy pamiętać, że przyrost dSi jest zawsze większy od 0.
Dla układu izolowanego (dQe=0)
proces quasi statyczny: dSi=0 proces nieodwracalny: dSi>0
dS=0 S= const dS>0, S2>S1
Wniosek: W układzie izolowanym entropia nie może maleć.
Dla układu wymieniającego ciepło z otoczeniem (dQe≠0)
proces quasi- statyczny: dSi=0 proces nieodwracalny dSi>0
dS=dQe/T dS>dQe/T
Wniosek: w układach wymieniających ciepło z otoczeniem przyrost entropi dS nie może być mniejszy od dQe/T.
W układach wymieniających ciepło z otoczeniem przyrost entropii dS może być większy lub mniejszy od zera, może też być zerem. Zależy to od znaku oraz od wartości entropii dSe wymienionej z otoczeniem.
PYTANIE 207 ENERGIA WEWN I ENTALPIA- ich zachowanie się w procesach endo i egzetermicznych.
Ze względu na ciepło, które układ wymienia z otoczeniem reakcje chemiczne można podzielić na endotermiczne i egzotermiczne. Ciepło to zależy od tego czy reakcja zachodzi izochorycznie czy izobarycznie. W pierwszym przypadku miarą ciepła reakcji jest zmiana energii wewnętrzenej ΔU (V=const), a w drugim zmiana entalpii ΔH (p=const). Rozróżnianie energii wewn i entalpii jako miar ciepła jest konieczne tylko w przypadku gazów, natomiast w przypadku cieczy i ciał stałych praktycznie ΔU= ΔH ze względu na małe zmiany objętości.
PYTANIE 208 ENERGIA SWODOBNA ENTALPIA SWOBODNA.
W procesach zachodzących izotermicznie kierunek ich przebiegu wyznacza energia swobodna F (w przemianach izochorycznych) oraz entalpia swobodna G (w przemianach izobarycznych.
Energia swobodna wynika z pierwszej i drugiej zasady termodynamiki, gdyż zgodnie z 1 zasadą: ΔU= ΔQ+ΔW czyli (-ΔW)= (-ΔU) + ΔQ, gdzie: (-ΔW)- praca wyk przez układ
(-ΔU)- ubytek energii wewnętrznej
ΔQ- ciepło wymienione z otoczeniem
Natomiast zgodnie z 2 zasadą termodynamiki ΔQ≤ T*ΔS (znak równości dotyczyłby procesów odwracalnych, a nierówności procesów nieodwracalnych), zatem:
(-ΔW)≤ (-ΔU)+ (T*ΔS)
Powyższy wzór dla procesów izotermicznych przyjmuje postać:
(-ΔW)≤ -Δ(U-TS) dla T=const
Zatem o pracy jaką może wykonać układ decyduje wielkość F:
F= U- TS
Powyższy wzór dla procesów izotermicznych może przyjąć postać:
ΔF= ΔU- T*ΔS
Wielkość F nazwana jest energią swobodną
W procesach izotermicznych ubytek energii swobodnej (-ΔF) jest równy pracy wykonanej przez układ (-ΔW), jeżeli proces przebiega odwracalnie; jest natomiast większy od pracy wykonanej, jeżeli proces jest nieodwracalny. Ubytek energii swobodnej układu wyraża więc maksymalną pracę, jaką może wykonać układ:
(-ΔF)= (-ΔW).
W procesie nieodwracalnym tylko część energii swobodnej ΔF'< ΔF zostaje wykorzystana jako praca, zaś reszta ΔF- ΔF'= ΔQ' zostaje rozproszona w postaci ciepła (tzn. zjawisko dyssapacji energii).
Z wzoru U=F+TS wynika, że niecała energia wewn. może być wykorzystana do wykonania pracy, a tylko jej część równa energii swobodnej F= U- TS, zaś pozostała część (TS) to energia związana, będąca energią nieużyteczną, która nie nadaje się do wykonania pracy. Energia swobodna F stanowi więc tę część energii wewn. układu, która w odpowiednich warunkach może być wykorzystana jako praca.
Jeżeli układ nie wykonuje pracy, nawet objętościowej to ΔW=0, proces przebiega izochorycznie, gdyż ΔV=0, więc zależność (-ΔF)= (-ΔW) przyjmie postać:
ΔF≤0
Zależność ta mówi o tym, że wyłączając zachodzące w układzie procesy odwracalne, dla których energia swobodna układu zachowuje wartość stałą, procesy izotermiczno- izochoryczne mogą przebiegać samorzutnie wyłącznie w kierunku zmniejszania się energii swobodnej (ΔF<0). Przyjmuje ona wartość najmniejszą w stanie równowagi. W ten sposób udowodniliśmy, że energia swobodna wyznacza kierunek procesu a ponadto stan równowagi układu.
Entalpia swobodna G
Entalpia swobodna zwana także potencjałem termodynamicznym Gibbsa lub potencjałem termodynamicznym pełni podobną rolę w procesach izotermiczno-izobarycznych co energia swobodna w procesach izotermiczno- izochorycznych.
Na pracę w procesie izobarycznym składa się praca objętościowa wykonana przez układ: (-ΔWobj)= pΔV, a ponadto układ może wykonać jakąś inną pracę (-ΔWi). Wówczas całkowita praca wykonana przez układ będzie wynosiła:
(-ΔW)= pΔV+ (-ΔWi), a po przekształceniu otrzymamy, że praca nieobjętościowa wykonana przez układ wynosi:
(-ΔWi)= (-ΔW)- pΔV
Jeśli podstawimy za (-ΔW) wyrażenie (-ΔW)≤ (-ΔU)+ (TΔS) to dla procesów izotermiczno-izobarycznych można otrzymać zależność:
(-ΔWi)≤ -Δ(U+ pV- TS), gdzie U+ pV= H to entalpia układu, zatem:
(-ΔWi)≤ -Δ(H-TS).
Wilekość G= H-TS nazywa się entalpią swobodną, która dla procesów izotermicznych może przyjąć postać:
ΔG= ΔH- TΔS
Korzystając z powyższego wzoru i wiedząc, że (-ΔWi)≤ -Δ(H-TS) można otrzymać zależność:
(-ΔG)≥(-ΔWi ) dla T=const i p=const
Z powyższego wzoru wynika treść fizyczna funkcji G: W procesach izotermiczno- izobarycznych ubytek entalpii swobodnej jest równy pracy nieobjętościowej (-ΔWi) wykonanej przez układ w procesie odwracalnym, jest natomiast większy od tej pracy, jeżeli proces przebiega nieodwracalnie.
Gdy układ poza pracą objętościową nie wykonuje innej pracej wtedy:
(-ΔG)> 0
Z zależności tej (pomijając procesy odwracalne) wynika następujące prawo: Procesy izotermiczno- izobaryczne mogą w układzie przebiegać samorzutnie wyłącznie w kierunku zmniejszania się entalpii swobodnej. Przyjmuje ona wartość najmniejszą w stanie równowagi układu.
- zmiana entropii dS może być spowodowana procesami nieodwracalnymi, tworzącymi entropię (dSi>0) oraz wymianą entropii z otoczeniem (dSe</>0), związaną z wymianą energii czy substancji
- w stanie stacjonarnym układu otwartego dSi/dt > 0
- szybkość tworzenia entropii
211. Charakterystyka termodynamiczna stanu stacjonarnego układu izolowanego i otwartego
Układ izolowany |
Układ otwarty |
- za wzrost entropii odpowiedzialne są tylko zachodzące w nim procesy nieodwracalne, czyli procesy tworzące entropię
- w stanie równowagi układu izolowanego dSi/dt =0
- szybkość tworzenia entropii
|
- zmiana entropii dS może być spowodowana procesami nieodwracalnymi, tworzącymi entropię (dSi>0) oraz wymianą entropii z otoczeniem (dSe</>0), związaną z wymianą energii czy substancji
- w stanie stacjonarnym układu otwartego dSi/dt > 0
- szybkość tworzenia entropii
|
- szybkość dSe /dt , z jaką entropia jest wymieniana z otoczeniem
- szybkość dSi /dt, z jaką entropia jest tworzona przez zachodzące w układzie procesy nieodwracalne
I wtedy:
dS/dt = dSe /dt + dSi /dt
Musi być: dSi /dt >= 0 , więc:
Szybkość tworzenia się entropii w układzie:
- nie może być „-”;
- jest 0 dla procesów odwracalnych,
- „+” dla nieodwracalnych.
Ale : szybkość, z jaką zmienia się entropia układu dS/dt może być „+” (zwiększa się), „-” (zmniejsza się) lub 0 (nie zmienia się) - to zależy od znaku dSe /dt, bo dSi /dt jest zawsze „+”.
Entropia układu się nie zmienia, jeśli dS/dt =0 i wtedy: dSi /dt = - dSe /dt
(entropia wytworzona w układzie w jednostce czasu jest równa entropii efektywnie oddanej w jednostce czasu do otoczenia).
Jeżeli układ otrzymuje w jednostce czasu z otoczenia entropię dSe`/dt, a oddaje dSe”/dt, to różnica
dSe /dt = dSe`/dt - dSe”/dt ujemna przy | dSe”/dt | > dSe`/dt
jest kompensowana szybkością tworzenia się entropii dSi /dt
W tych warunkach entropia układu się nie zmienia (S=const); układ znajduje się w tzw. stanie stacjonarnym. Rośnie natomiast entropia otoczenia. Jeśli otoczenie wliczymy do układu, otrzymamy układ izolowany, w którym entropia się zwiększa zgodnie z II zas. termodynamiki.
W stanie stacjonarnym funkcje termodynamiczne układu zachowują stałą wartość w czasie - stała entropia, energia, entalpia swobodna. Funkcje te też są stałe w układzie izolowanym, w stanie równowagi, ale stan stacjonarny układu otwartego różni się od stanu równowagi układu izolowanego.
212.
W stanie stacjonarnym funkcje termodynamiczne układu zachowują stałą wartość w czasie - stała entropia, energia, entalpia swobodna. Funkcje te też są stałe w układzie izolowanym, w stanie równowagi, ale stan stacjonarny układu otwartego różni się od stanu równowagi układu izolowanego.
ZASADA PRIGOGINE'A
Brzmienie:
W stanie stacjonarnym szybkość tworzenia się entropii jest stała i przyjmuje wartość najmniejszą.
W stanie stacjonarnym w układzie zachodzą procesy tworzące entropię dSi/dt > 0 - wykres.
(dla odróżnienia: w stanie równowagi dSi/dt =0, a entropia przyjmuje wartość maksymalną (energia swobodna minimalna)).
Ryc. 5.2. w Pilawskim to (wg dr S.) ilustracja wniosku z zasady Prigogine'a : zmiana bodźca Xi powoduje wzrost szybkości tworzenia entropii, przywracający stan stacjonarny.
214. Potencjał elektrochemiczny, definicja, rola
Jeżeli układ zawiera cząsteczki mające ładunek elektryczny (elektrolity, koloidy), to zmiana liczby moli jakiegoś ze składników może się wiązać z wykonaniem pracy nie tylko chemicznej ΔWch, ale takze elektrycznej ΔWel . Zmiana entalpii swobodnej składnika i o Δni moli wyraża się zależnością:
ΔWi= ΔGi= ΔWch+ ΔWel
Praca chemiczna:
Δ Wch=
μi Δni
Praca elektryczna:
ΔWel= ψΔqi
Wyraża zmianę energii układu spowodowaną zmianą ładunku elektrycznego Δqi przy potencjale elektrycznym φ. Przy czym ładunek elektryczny składnika i , przy zmianie jego ilości o Δni moli zmienia się o :
Δqi = zF Δni
z - liczba ładunków elementarnych związanych z cząsteczką
F - stała Faradaya
Zmiana entalpii swobodnej bedąca wynikiem zmiany liczby moli substancji i o Δni
wynosi :
ΔGi = φ zF Δni + μ Δni
Potencjał elektrochemiczny to zmiana entalpii swobodnej na 1 mol, czyli:
Potencjał elektrochemiczny odgrywa tę samą rolę w układzie zawierającym ładunki elektryczne co potencjał chemiczny w układzie bez ładunków elektrycznych.
215. Potencjał elektrodowy
Zanurzając metal do roztworu elektrolitu z kationami tego metalu zachodzi reakcja:
5.11
Atomy metali, pozostawiając elektrony walencyjne, w postaci jonów przechodzą do roztworu. Na granicy metalu i roztworu tworzy się podwójna warstwa ładunków elektrycznych przeciwnego znaku. Dodatni ładunek elektrolitu hamuje dalszy dopływ kationów z metalu.
Przy określonej różnicy potencjałów między metalem a elektrolitem ustala się stan równowagi, wtedy reakcja powyższa przebiega w obie strony z jednakową szybkością , a proces można uznać za odwracalny. W tych warunkach różnica potencjałów elektrycznych między metalem a elektrolitem zwana jest potencjałem elektrodowym delta V danego metalu wyraża się wzorem Ernsta:
5.12
Plus rycina 5.6-Pilawski
Delta Vo jest równe różnicy potencjałów przy jednostkowym stężeniu jonów w elektrolicie i nosi nazwę potencjału standardowego. Potencjału tego nie można zmierzyć bezpośrednio, wyraża się go umownie różnicą potencjału ogniwa , w którym drugą elektrodą jest elektroda wodorowa , czyli platyna opłukiwana wodorem przy ciśnieniu 101,3 kPa , zanurzona w roztworze o jednostkowym stężeniu jonów wodorowych w temperaturze 298K.
Potencjał elektrodowy odgrywa ważną rolę przy pomiarach elektrofizjologicznych np. potencjałów bioelektrycznych.
Jeżeli 2 elektrody z tego samego metalu zanurzone w roztworach ich soli o różnym stężeniu, czyli 2 półogniwa, połączyć kluczem elektrolitycznym(rurka szklana wypełniona agarem z roztworem KCL lub NH4NO3) w celu uniknięcia mieszania się elektrolitów, to otrzymuje się ogniwo stężeniowe.
Siła elektromotoryczna takiego ogniwa wyrazi się wzorem Nernsta:
Wzór ten otrzymuje się jako różnicę dwóch potencjałów elektrodowych:
Plus rycina 5.7-schemat ogniwa(Pilawski)
218. Równowaga donnanowska
Błona rozdziela roztwory zawierające po jednej stronie aniony białkowe B- i kationy K+ o stężeniu c1, po drugiej aniony Cl- i kationy K+ o stężeniu c2. Błona nie przepuszcza jonów białkowych. Jony Cl- dyfundują wtedy z przestrzeni II do I.
W celu zachowania równowagi elektrycznej pociągają za sobą jony K+. Błona ładuję się i przy określonej różnicy potencjałów ΔV ruch jonów zostaje zatrzymany, ustali się stan równowagi przy określonych stężeniach po obu stronach błony.
Porównanie potencjałów elektrochemicznych prowadzi do warunku równowagi, wyrażającego się zależnością
Potencjał błonowy wyraża się wzorem
Wzór ten odpowiada stanowi równowagi. Teoria Donnana nie uwzględnia transportu aktywnego.
219. Potencjał chemiczny, definicja i rola
Zmiana entalpii swobodnej jakiejś substancji, w pewnym obszarze układu , może być wynikiem zmiany jej ilości spowodowanej wymianą z otoczeniem , wejściem w reakcję chemiczną, zmianą fazy, itp. Każdy z tych procesów związany jest z wykonaniem pracy (praca chemiczna, osmotyczna, transportu itp.). Jeżeli proces zachodzi quasi-statycznie, miarą pracy Δ Wi
wykonanej jest zmiana entalpii swobodnej.
Δ Wi = ΔGi
Zmiana entalpii swobodnej jest proporcjonalna do zmiany liczby moli Δni
substancji i, czyli:
Δ Wi = ΔGi
Δni
Współczynnik proporcjonalności
nosi nazwę potencjału chemicznego substancji i.
Entalpię swobodną substancji i należy uważać jako funkcję wielu zmiennych :
Gi=
,…,nN
)
Żeby proces zachodził quasi-statycznie, zmiana liczby moli substancji musi być nieskończenie mała δn, powodując nieskończenie małą zmianę entalpii swobodnej δG, wtedy potencjał chemiczny µi wyrazi się pochodną cząstkową:
µi=(δG/δni)T
P=const
T=const
const j
Potencjał chemiczny składnika i wyraża liczbowo pracę wykonaną podczas zmiany liczby moli tego składnika o jeden, przy zachowaniu stałości temperatury, ciśnienia oraz ilości innych składników wchodzących w skład układu. Praca wyrażona wzorem : Δ Wi = ΔGi
Δni
nosi nazwę pracy chemicznej lub pracy osmotycznej, lepiej odpowiada nazwa praca transportu.
Potencjał chemiczny składnika i wyraża się wzorem:
- potencjał chemiczny składnika i w stanie czystym (
, w temperaturze T i przy ciśnieniu p.
Powyższy wzór jest również stosowany dla roztworów doskonałych, czyli roztworów, w których zaniedbać można oddziaływania międzycząsteczkowe; w przybliżeniu warunek ten spełniają roztwory bardzo rozcieńczone.
Dla roztworów rzeczywistych, w celu uwzględnienia oddziaływań międzycząsteczkowych wprowadza się zamiast stosunku molowego pojęcie aktywności ai. Spełniona ma być zależność:
Aktywność ai składnika i definiuje się wzorem:
ai
Współczynnik proporcjonalności fai nosi nazwę współczynnika aktywności. Wyznacza się go doświadczalnie. Dla roztworów rzeczywistych wynosi 1.
Zamiast stosunku molowego xi wprowadza się często stężenie roztworu ci. Wtedy wzór przyjmuje postać:
Dla roztworów rzeczywistych należy zamiast stężenia stosować aktywność stężeniową, wtedy:
gdzie aci
- współczynnik aktywności (stężeniowy)
Rola Potencjału chemicznego:
-ocena stanu układu pod względem możliwości zachodzenia w nim transportu materii.
Jeżeli w układzie istnieją różnice potencjałów chemicznych, zachodzą w nim procesy fizyczne lub chemiczne związane z transportem substancji, zmieniająca skład układu. Różnice potencjałów chemicznych stanowią więc rodzaj „sił napędowych” zwanych bodźcami termodynamicznymi transportu substancji. W stanie równowagi różnice potencjałów chemicznych zanikają, potencjały chemiczne składników układu przyjmują wartości minimalne.
Przykłady zjawisk wywołanych różnicą potencjałów chemicznych, prowadzących do stanów równowagi układu są zjawiska dyfuzji i osmozy.
220. Dyfuzja przez błonę, jeżeli dwa roztwory o stężeniach molowych
oraz
będą rozdzielone błoną utrudniającą dyfuzję, to prawo Ficka, daje się zapisać w postaci:
Gdzie:
szybkość dyfuzji, wyrażona stosunkiem liczby moli
przepływających przez powierzchnię
do czasu
,
- przepuszczalność błony dla danej substancji, wyrażona w m/s jeśli stężenie jest w mol/
Chociaż wzór ten jest uproszczeniem, gdyż dyfuzja w tym przypadku jest zakłócona różnicą ciśnień osmotycznych, jest on stosowany do opisu transportu przez błony biologiczne.
221. Transport przez błonę.
Błony biologiczne nie są doskonale półprzepuszczalne, wykazują różną dla różnych substancji przepuszczalność; stosowanie do nich zwykłych praw dyfuzji i osmozy jest dużym uproszczeniem. Problem należy rozpatrzeć z punktu widzenia termodynamiki nierównowagowej.
Miarą właściwości wybiórczego przepuszczania błony jest współczynnik odbicia
, wyrażający się stosunkiem ciśnień:
Gdzie:
- ciśnienie napiętej błony,
- różnica ciśnień osmotycznych
Dla błon biologicznych 0<
, ciśnienie z jakim działa błona na wnętrze komórki nie jest zrównoważone różnicą ciśnień osmotycznych.
Gęstość strumienia roztworu tłoczonego przez błonę jest:
Gdzie:
- współczynnik filtracji
Transport przez błonę jest zjawiskiem dynamicznym. W związku z przenikaniem substancji przez błonę jest ona mniej napięta niż w przypadku błony półprzepuszczalnej, czyli
zmniejsza się w stosunku do
. Komórki żywe nie znajdują się w stanie równowagi termodynamicznej, lecz stanie stacjonarnym. Utrzymanie tego rodzaju stanu wymaga podtrzymywania bodźców, np. w postaci różnicy stężeń, wtedy oprócz transportów biernych w kierunku zgodnym z działaniem bodźców będą istnieć transporty wymuszone. Transporty wymuszone odbywające się w kierunku przeciwstawnym bodźcom, wymagają nakładu energii i nazywane są transportami aktywnymi.
223. Prawo van't Hoffa określa ciśnienie osmotyczne:
Gdzie:
- stężenie molowe, R - stała gazowa, T - temperatura
Ciśnienie osmotyczne jest proporcjonalne do stężenia molowego i do temperatury. Ciśnienie osmotyczne zależy więc od liczby cząsteczek rozpuszczonych w jednostce objętości, nie zależy natomiast od rodzaju ciała rozpuszczonego.
Przy stosowaniu prawa van't Hoffa w stosunku do elektrolitów należy uwzględnić stopień dysocjacji; jony stanowią bowiem samodzielne cząstki.
224. Filtracja
Roztwory o jednakowych w stanie wyjściowym stężeniach są przedzielone błoną przepuszczającą zarówno rozpuszczalnik, jak i ciało rozpuszczone (ryc 5.5). Różnica ciśnień
spowoduje przepływ roztworu, gęstość strumienia o objętości
jest proporcjonalna do różnicy ciśnień, czyli:
c = 0)
Tego rodzaju transport uwarunkowany różnicą ciśnień hydrostatycznych nazywa się filtracją, a
jest współczynnikiem filtracji.
225. Ultrafiltracja.
Zachodzi dla roztworów o takich samych stężeniach substancji rozpuszczonej, przedzielonych błoną przepuszczającą wybiórczo rozpuszczalnik i substancję rozpuszczoną, między którymi istnieje różnica ciśnień hydrostatycznych Δp. Przepływy Jr -rozpuszczalnika i Js - substancji rozpuszczonej, będą uwarunkowane różnicami potencjałów chemicznych między roztworami przedzielonymi błoną i przepuszczalnością błony.
Potencjały chemiczne nie będą jednakowe, ponieważ potencjał zależy od ciśnienia.
Przepływowi Jr- rozpuszczalnika, towarzyszy przepływ Js - substancji rozpuszczonej, jednak pomniejszony o mniej przepuszczającą błonę.
Względna gęstość strumienia objętości Jd substancji w stosunku do rozpuszczalnika wynosi:
(dla Δc = 0)
Ldv - współczynnik ultrafiltracji
Δp - różnica ciśnień hydrostatycznych
Jd - względna gęstość strumienia obj. Jd substancji w stosunku do rozpuszczalnika.
Warte zaznaczenia jest to że powyższy wzór nie jest do końca prawdziwy bo mówi on o sytuacji wyjściowej kiedy różnica ciśnień substancji w roztworach jest równa 0, ale podczas przebiegu procesu tworzy się różnica stężeń subst. za sprawą różnej przepuszczalności błony dla subst. rozpuszczonej i rozpuszczalnika, co powoduje powstanie ciśnienia osmotycznego skierowanego w przeciwną stronę, jest to przykład procesów sprzężonych które przedłużają życie układu.
226. Wyznaczanie masy molowej metodą ciśnienia osmotycznego.
Przy określaniu masy molowej należy wyjść z prawa vant' Hoffa, czyli:
R - stała gazowa
T - temperatura w Kelwinach
Π - ciśnienie osmotyczne
Cm - stężenie molowe
Ciśnienie osmotyczne zależy od liczby cząsteczek ciała rozpuszczonego w jednostce obj. Nie zależy natomiast od rodzaju ciała rozpuszczonego.
Prawo van't Hoffa można zapisać w postaci (to jest właściwy wzór który trzeba umieć! Ale poprzedni też dobrze znać):
C=m/V - stężenie masowe (inaczej molane)
Mm - masa molowa subst. Rozpuszczonej
*Dla roztworów rzeczywistych trzeba do tego wzoru wprowadzić poprawki.
227. Energia powierzchniowa, napięcie powierzchniowe
Energia powierzchniowa właściwa - lub współczynnik napięcia powierzchniowego - napięcie powierzchniowe - stycznie do powierzchni cieczy działają siły zwane siłami napięcia powierzchniowego starające się zmniejszyć swobodną powierzchnię cieczy.
(Ryc. 6.16 str. 102 Jaroszyk) W celu utrzymania stałego pola powierzchni błony mydlanej rozpiętej na ramce z drutu, trzeba na ruchome ramię ramki działać siłą F. Wymaga to zrównoważenia wypadkowej sił napięć powierzchniowych zaczepionych wzdłuż ramienia o długości L=2l (2l - bo siły działają po obu stronach błony).
Zwiększenie pola błony o ∆S=L ∙ ∆x wymaga wykonania pracy ∆W=F ∙ ∆x , stąd napięcie powierzchniowe wyraża wzór:
σ=∆W/∆S = F ∙ ∆x/L ∙ ∆x
σ=F/L [σ]=J/m² = N/m
F - siła napięcia powierzchniowego działająca równolegle do powierzchni cieczy, dążąca do zmniejszenia powierzchni cieczy,
L - długość odcinka na którym działa siła
Napięcie powierzchniowe wyraża się stosunkiem wypadkowej sił napięcia powierzchniowego do długości odcinka, wzdłuż którego są zaczepione.
228. PRAWO LAPLACE'A
Jest związane ze stanami powierzchniowymi zakrzywionej powierzchni cieczy. Stany te powodują, że pod zakrzywioną powierzchnią cieczy panuje inne ciśnienie aniżeli pod płaską. W przypadku powierzchni wypukłych ciśnienie to jest większe, natomiast w przypadku wklęsłych mniejsze - jak w przypadku powierzchni płaskich. Wartość nadwyżki ciśnienia p dla cieczy w kształcie kuli wyraża wzór Laplace'a:
p=2sigma/r gdzie: sigma-napięcie powierzchniowe
r-promień powierzchni kulistej
dla cieczy o różnych krzywiznach:
p= sigma(1/R1 + 1/R2)
gdzie: R1 i R2 to promienie krzywizny powierzchni cieczy w dwóch do siebie prostopadłych przekrojach
dla walca:
p=sigma/R
Prawo Laplace'a znazło szerokie zastosowanie w analizach biofizycznych, np. w ocenie ciśnienia w naczyniu krwionośnym, w pęcherzykach płucnych, itp.
234. Roztwory stałe. Stopy. (zamiast pytania: sieć doskonała i rzeczywista, bo tego materiału nie ma w rozpisce)
Roztwór stały - jednorodna pod względem fizycznym krystaliczna mieszanina dwóch lub więcej izomorficznych substancji, znajdująca się w stałym stanie skupienia. Mieszaninę taką traktuje się, jako roztwór, jeżeli po dodaniu substancji rozpuszczonych struktura krystaliczna rozpuszczalnika nie zmienia się i roztwór ten pozostaje w pojedynczej fazie jednorodnej.
Stopy stanowią roztwory stałe, co najmniej dwóch metali. Są często stosowane w medycynie, jako wszczepy(implanty). Cechy, którymi powinien się charakteryzować materiał tworzący wszczep: zgodność biologiczna, odporność na korozję, odpowiednia wytrzymałość statyczna i zmęczeniowa, plastyczność.
Podstawowe informacje o możliwości tworzenia stopów uzyskujemy z diagramów fazowych wykreślanych na podstawie analizy termicznej- pomiarze zmian temperatury próbki w czasie jej równomiernego ogrzewania lub ochładzania( przykładowe str. 109, Jaroszyk). (Str. 126 tegoż samego pana- wykresy)
Informacje o teksturze otrzymanych faz dostarcza analiza mikroskopowa.
Substancje izomorficzne wykazują nieograniczoną rozpuszczalność w fazie stałej, częściej występują stopy o ograniczonej rozpuszczalności.
Innym rodzajem stopów są stopy międzywęzłowe- składniki o dużej różnicy promieni atomowych.
239. Widma dźwięków
Widmo jest fizycznym aspektem dźwięku, określa rozkład natężenia składowych dźwięku w zależności od jego częstotliwości. Ze strukturą widmową wiążę się barwa dźwięku.
Ze względu na rodzaj widma dźwięki klasyfikuje się następująco:
1) ton (dźwięk prosty) - drganie sinusoidalne o jednej częstości. Widmo liniowe, o brzmieniu ubogim.
2) wieloton harmoniczny (dźwięk złożony) - drganie będące sumą drgań sinusoidalnych o częstościach będących wielokrotnościami (1,2,3,...) częstości podstawowej. Widmo liniowe, o brzmieniu złożonym.
3) wieloton nieharmoniczny - ich częstotliwości nie są całkowitą wielokrotnością częstotliwości podstawnej. drganie będące sumą nie uporządkowanych drgań. O brzmieniu ostrym.
4) szum - dźwięk o widmie ciągłym lub ciągłym w pewnych zakresach częstotliwości.
Dla fal okresowych częstotliwości składowych, dla których natężenie jest różne od zera, tworzą ciąg oddzielnych wartości - widmo liniowe.
Dla przebiegów falowych nieokresowych widmo zawiera ciągłe przedziały częstotliwości - widmo ciągłe.
240. Poziom głośności. Jednostki.
Poziom głośności określa relacje między głośnością dźwięku a odpowiadającym mu natężeniem dźwięku. Jako miarę poziomu głośności Ln przyjmuje się poziom natężenia głośności tonu o częstotliwości 1000 Hz, który jest słyszany jednakowo głośno jak ton badany.
Fon - jednostka poziomu głośności. Liczba fonów tonu ocenianego jest równa liczbie decybeli tonu o częstotliwości 1000 Hz słyszanego tak samo głośno. Dla tonu 1000 Hz o różnych natężeniach liczba fonów jest równa liczbie decybeli. Wszystkie tony o natężeniu progowym mają poziom głośności równy 0 fonów.
Poziom głośności : wielkość subiektywna i względna.
Pytanie 241: Natężenie dźwięku, poziom, jednostki
Natężenie dźwięku I to stosunek mocy P dźwięku przechodzącego przez powierzchnię jednostkową A
I = P/A [I] = 1 W/m2
I = P/A = W/A*t, gdzie W - praca sił parcia w jednostce czasu t
Próg słyszalności - najmniejsze słyszalne natężenie dźwięku I0=10-12 W/m2 (dla tonu 1000 Hz) lub p0=2*10-5 Pa
Próg bólu - Imax=1 W/m2 lub pmax=2*10 Pa
Poziom natężenia dźwięku L - logarytm stosunku natężenia dźwięku badanego I do natężenia odniesienia I0.
L=lg(I/I0) (w belach)
L=10 lg(I/I0) (w decybelach)
Gdzie I0=10-12 W/m2 [L]=1 dB
Dla progu słyszalności L=0 B
Dla progu bólu L=12 B
Poziom natężenia dźwięku można zastąpić poziomem ciśnienia akustycznego z zależności I~pm2
L=lg(pm/p0)2=2 lg (pm/p0) (w belach)
L=20 lg (pm/p0) (w decybelach) , gdzie p0=2*10-5 Pa
Pytanie 242: Prawo Webera - Fechnera
Stosuje się go do zmysłów.
Najmniejszy zauważalny przyrost bodźca (próg różnicy ∆I0), jest proporcjonalny do natężenia I bodźca już działającego.
∆I0 / I = const
Przy upraszczających założeniach: przyrost głośności jest proporcjonalny do logarytmu stosunku natężeń dźwięków porównywalnych.
Pytanie 243: Krzywe izofoniczne
Krzywe jednakowego poziomu głośności dźwięku to krzywe izofoniczne. Izofony (krzywe izofoniczne) są przedstawione w układzie logarytmicznej zależności poziomu natężenia dźwięku lub poziomu ciśnienia akustycznego od częstotliwości. Krzywe są dlatego, że nasz zmysł słuchu nie ma „liniowej charakterystyki przetwarzania”. Głośność dźwięku określa się przez porównanie wrażenia wywołanego przez dany dźwięk z wrażeniem wywołanym przez dźwięk o częstotliwości wzorcowej 1 kHz.
Izofony "normalnego" ucha wg Fletchera i Munsona. Wartości fonów są oznaczone na niebiesko.
Najniżej położona krzywa (0 fonów) stanowi próg słyszalności, czyli określa najmniejszą wartość poziomu głośności dźwięku o danej częstotliwości wywołującego wrażenie słuchowe. Krzywa położona najwyżej (ok. 120 fonów) stanowi granicę bólu co oznacza że tony o określonych przez nią poziomach powodują ból, a nawet mogą uszkodzić słuch.
Dolna granica słyszalności i granica bólu wyznaczają obszar (powierzchnię) słyszalności.
Ze względu na swój subiektywny charakter, krzywe izofoniczne nie maja ścisłego kształtu, ani położenia i różnią się w zależności od metod badawczych użytych do ich wyznaczenia.
Izofony wykorzystuje się w badaniach słuchu, telekomunikacji.
Fon - jednostka poziomu głośności dźwięku. Poziom głośności dowolnego dźwięku w fonach jest liczbowo równy poziomowi natężenia (wyrażonego w decybelach) tonu o częstotliwości 1 kHz, którego głośność jest równa głośności tego dźwięku. Dźwięki o tej samej liczbie fonów wywołują to samo wrażenie głośności, ale nie muszą być to dźwięki identyczne w sensie barwy (np. o różnych częstotliwościach).
Obecnie powszechnie stosuje się liniową jednostkę głośności dźwięku wyrażoną w sonach.
1 son odpowiada głośności tonu o częstotliwości 1000 Hz i natężeniu 40dB.
N=20,1(LN-40) w przybliżeniu lgN = 0,03(LN-40)
LN - liczba fonów
N - son
Pytanie 244: Hałas, wielkości wpływające na skutki działania hałasu.
HAŁAS = niepożądane, dokuczliwe dźwięki, szkodliwe dla zdrowia (narząd słuchu, układ nerwowy,
zaburzenia niektórych procesów biochemicznych)
Dłuższe przebywanie w hałasie ubytek słuchu (NIEODWRACALNY!) + podwyższenie progu
słyszalności (TRWAŁE!)
- próg słyszalności: L = 0 B
- próg bólu: L = 12 B = 120 dB
Walka z hałasem = problem ochrony środowiska, problem społeczny.
UWAGA!!! Nie wiem o co dokładnie im chodzi w drugiej części pytania… Ale może o to…
Wielkości wpływające na skutki hałasu:
-poziom natężenia dźwięku L:
L= lg I/Io (w belach) = 10 lg I/I0 (w decybelach), gdzie:
I - natężenie dźwięku badanego
I0 - natężenie dźwięku odniesienia (przyjmujemy za nie natężenie progowe tonu 1000 Hz, czyli 10-12 W/m2 )
Dla 1000 Hz zakres wynosi od 0 do 12 B.
Poziom natężenia dźwięku można zastąpić poziomem ciśnienia akustycznego.
L= lg (pm/p0)2 = 2 lg pm/p0 (w belach)
-częstotliwość: związana z wysokością dźwięku
Ucho słyszy dźwięki w zakresie częstotliwości 16 - 20 000 Hz.
Drgania o niższej częstotliwości= INFRADŹWIĘKI i o wyższej częstotliwości=ULTRADŹWIĘKI również mogą być szkodliwe dla ucha!
-poziom głośności dźwięku LN:
Jest to taki poziom natężenia głośności tonu o f=1000 Hz, który jest słyszany jednakowo głośno jak ton badany. Jednostka to fon. Wszystkie tony o natężeniu progowym mają poziom głośności 0 fonów!!!
Obecnie skala głośności wyrażana jest w sonach: N=2 0,1(LN-40), w przybliżeniu lg N ≈ 0,03(LN-40).
Znalazłam przydatną prezentację na temat hałasu: http://www.chemia.pk.edu.pl/wydzial/pliki/HAlAS%20I%20WIBRACJE_studenci.pdf
Pytanie 245: Rola kostek słuchowych w transporcie fali w uchu, mechanizm wzmacniania dźwięku.
Kosteczki słuchowe ucha środkowego: młoteczek, kowadełko, strzemiączko przekazują ruch drgający z bębenka (który jest wynikiem zmiany ciśnienia po dojściu fali głosowej) na błonę okienka owalnego. Drgania błony okienka owalnego wprowadzają w ruch perylimfę wypełniającą przewody ślimaka. Ciśnienie potrzebne do tego celu zapewnia ucho środkowe, które pełni rolę wzmacniacza. Amplituda drgań zostaje co prawda zmniejszona, ale zwiększone zostaje ciśnienie. Wzmocnienie to zostaje uzyskane w następujący sposób: układ kosteczek słuchowych działa jako dźwignia (ryc.11.10), dzięki czemu na okienko owalne działa siła F2=(r1/r2)F1; ponadto powierzchnia działania siły F2 na okienko owalne jest znacznie mniejsza od powierzchni działania siły F1 z bębenkiem. W ostatecznym rozrachunku przyjmuje się, że ciśnienie działające na okienko owalne jest ok. 17 razy większe od ciśnienia z jakim bębenek działa na młoteczek.
Układ kosteczek słuchowych uczestniczy także w dopasowywaniu oporności akustycznej ucha zewnętrznego i wewnętrznego (gdyby nie było kosteczek ponad 99,9% fali akustycznej z powietrza zostałoby odbite przez okienko owalne).
Ucho środkowe chroni też ucho wewnętrzne przed przeciążeniem dźwiękami o zbyt dużym natężeniu. Przy zbyt dużych siłach strzemiączko zamiast uciskać okienko owalne z większą siłą, wykonuje ruchy skręcające. Dodatkowe tłumienie jest spowodowane działaniem mięśni, które kurcząc się, usztywniają układ kosteczek słuchowych i napinają bębenek.
Pytanie 246: Ucho - odbiornik, teoria Bekesy'ego.
Według teorii Bekesy'ego, drgania błony okienka owalnego wprowadzają w ruch perilimfę. Pojawia się różnica ciśnień między schodami przedsionka, a schodami bębenka, powoduje ona odkształcenie błony podstawnej. Odkształcenie to w postaci impulsu falowego rozchodzi się wzdłuż błony. Maksimum odkształcenia błony dla częstotliwości wysokich, wypada bliżej okienka owalnego (błona jest bardziej napięta i węższa), im częstotliwość niższa tym maksimum znajduje się dalej od okienka. Maksimum odkształcenia błony podstawnej wypada więc w różnych miejscach, powodując pobudzenia komórek rzęsatych. Te z kolei wyzwalają impulsy nerwowe, przekazywane do układu ośrodkowego. W ten sposób ucho dokonuje analizy częstotliwości.
Nawet jeżeli maksimum odkształcenia błony nie jest wyraźnie zaznaczone, ucho zachowuje stosunkowo dużą zdolność do rozróżniania częstotliwości - okazuje się, że selektywność wyboru częstotliwości przez włókna nerwowe jest dokładniejsza niż by to wynikało z obszerności odkształcenia błony.
Wzrost natężenia bodźca powiększa częstotliwość impulsów nerwowych. Jest ona jednak ograniczona przepustowością włókna nerwowego, dlatego też informacja o natężeniu dźwięku musi być przekazywana jednocześnie przez większą liczbę włókien.
Pytanie 247: Obliczyć błąd względny (a*2-b*2)/4a.
Pytanie 248: Obliczyć błąd względny σ/σ0(ρη0/ρ0η).
Pytanie 249: Obliczyć błąd względny R=R0(I1/I2).
Pytanie 250: Obliczyć błąd względny f=(l2+d2)/4d2.
Pytanie 251: Błąd n=(R*K)/RK.
Pytanie 252: Błąd na lepkość.
η=[2r2g(ρ1- ρ2)t]/9h
g, ρ1, ρ2 - wielkości stałe, a=[2g(ρ1- ρ2)]/9
η=a[r2t/h]
ln η = ln a + ln r2 + ln t - ln h
ln η = ln a + 2 ln r + ln t - ln h
d ln η = 0 + 2 d ln r + d ln t - d ln h
d η/η = 2 d r/r + d t/t - d h/h
Δ η/η = 2 Δ r/r + Δ t/t + Δ h/h
(wszystkie wielkości są wartościami uśrednionymi)
Pytanie 253: Błąd względny refrakcji molekularnej.
Pytanie 254: Podział błędów.
Błędy dzielimy na:
Inny podział:
25256. BŁĄD BEZWZGLĘDNY DLA OPORNIKA ELEKTRYCZNEGO
Opór elektryczny(rezystancja)
R - opór elektryczny [1Ω]
U - napięcie [1V]
I - natężenie prądu [1A]
Metoda różniczki zupełnej
R(U,I)=U/I tzn. U i I są wartościami zmiennymi
d - oznacza pochodną , tzn z danej funkcji trzeba zrobić jej pochodną wg. wzoru f(x)= xn
to jego pochodna f(x)'= nxn-1
ΔR= ( dU/dIU)ΔU + (dU/dII)ΔI
Wiec ΔR=(1/I)ΔU +(U/-)ΔI
Metoda pochodej wartosci logarytmicznej
lnR=lnU - lnI
dlnR=dlnU-dlnI
∆R/R=∆U/U + ∆I/I
Liczniki- błędy standardowe
Mianowniki- wartości średnie
257. BŁAD STANDARDOWY= średni błąd średniej arytmetycznej
∆x= s/n
s- odchylenie standardowe
n - liczba pomiarów
obrazuje odchylenia średnich wyników prowadzonych niezależnie
258. ODCHYLENIE STANDARDOWE
odchylenie średnie wyników pomiarów tej samej wielkości otrzymanych przy użyciu tego samego narzędzia pomiarowego. Oznacza się go zwykle symbolem s i wyraża wzorem:
gdzie xi - i-ty wynik pomiaru,
- wartość średnia wyników pomiarów, n - liczba pomiarów.
260. Średnia arytmetyczna to taka miara, dla której suma wszystkich kwadratów odchyleń przyjmie wartość minimalną. Stosując ją, chcemy obliczyć minimum funkcji Ψ (formy kwadratowej), czyli taką wartość x , kiedy funkcja Ψ przyjmuje najmniejszą wartość.
Ψ=i=1nxi-x2
Aby znaleźć tą minimalną wartość funkcji, liczymy pochodną tej funkcji i przyrównujemy do zera. Rozwiązując poniższe równanie x będzie argumentem funkcji Ψ(x) dla którego funkcja ma minimalną wartość.
dΨdx =-2i=1nxi-x =0
-2i=1nxi-x =0 /÷-2
i=1nxi-x =0
i=1nxi-i=1nx=0
(Na podstawie wzoru: i=1nk=nk)
i=1nxi=nx /÷n
OSTATECZNY WZÓR NA ŚREDNIA ARYTMETYCZNĄ :
x=1ni=1nxi
261. Błąd systematyczny, dokładność pomiarów.
Błędy systematyczne wynikają z niewłaściwego wyskalowania przyrządów, np. za duże lub za małe odległości między liniami podziałki, opóźniający lub spieszący stoper, niewłaściwe ustawienie zegara w miernikach elektrycznych. Mogą one wynikać również z cech osobniczych osoby wykonującej pomiary - nadmierna lub opóźniona reakcja na bodziec. Wielkość błędów zależy od dokładności narzędzi pomiarowych- podziałka w śrubie mikrometrycznej co 0.01 mm oznacza dokładność pomiaru równą 0.01 mm, podziałka w wadze analitycznej co 1mg oznacza dokładność pomiaru równa 1mg, np. pomiar wyniósł 100mg (100 ± 1mg).
Błędy systematyczne można wyeliminować odpowiednio kalibrując przyrządy pomiarowe.
262. Błąd przypadkowy.
Błędy przypadkowe wynikają z chwilowej niedyspozycji bądź dekoncentracji osoby prowadzącej pomiary, np. zbyt głośne/ciche otoczenie, chwilowe wahania napięcia sieci przy wykorzystaniu mierników elektrycznych, chwilowe wahania temperatury, wilgotności powietrza. Błędów tych nie da się wyeliminować.
264. Zjawisko piezoelektryczne występuje w kryształach nie posiadających środka symetrii, np. kwarc.
Mechaniczne ściskanie przeciwległych płytek płaskorównoległych wyciętych z kryształu anizotropowego → deformacja powłok elektronowych atomów; przesunięcie dodatnich i ujemnych ładunków względem siebie → na płytkach pojawiają się ładunki przeciwnego znaku = powstaje między nimi napięcie elektryczne.
Zjawisko to działa też w drugą stronę: napięcie elektryczne przyłożone do przeciwległych powierzchni płytki powoduje mechaniczną deformację tej płytki.
Jeżeli przyłożone napięcie jest zmienne w czasie to płytka będzie wykonywać drgania z częstotliwością równą częstotliwości przyłożonego napięcia.
263. 2 typy głowic:
Służy takżę do niszczenia tkanek nowotworowych niezłośliwych przez lokalne podwyższenie temperatury nawet do 80-90st.C (metoda HIFU - High Intensity Focused Ultrasound )
265. Wzmocnienie w USG
Chodzi o Strefową Regulację Wzmocnienia, czyli metoda kompensacji strat sygnału polegająca na płynnym podwyższaniu wzmocnienia toru odbiorczego w miarę upływu czasu po nadaniu impulsu sondującego czyli w miarę wzrostu zasięgu, z którego powracają echa. (Internet)
266. Podstawy USG dopplerowskiego.
Metoda ta wykorzystywana jest w diagnostyce układu krążenia , pozwala na wyznaczenie średniej prędkości przepływu krwi w naczyniach, prędkości chwilowej krwi oraz na analizę rozkładu prędkości krwi w naczyniach. Pozwala także na analizę przepływu krwi w ciągu 1 sekundy.
Metoda ta jest oparta na zjawisku Dopplera, czyli pozornej zmianie częstotliwości źródła dźwięku wynikającej albo z ruchu źródła albo z ruchu obserwatora.
Głowica wysyła sygnał do naczyń krwionośnych który napotyka element upostaciowiony w ruchu (np. trombocyt).
Element oddala się od głowicy z prędkością v. Rejestruje on więc dźwięki o częstotliwości wyższej, element ten nie pochłania fali, lecz staje się wtórnym źródłem ultradźwięków o częstotliwości f2.
Głowica jest teraz obserwatorem a trombocyt źródłem.
Teraz źródło oddala się od obserwatora, więc głowica rejestruje fale o częstotliwości f1.
gdzie: c- prędkość ultradźwięków we krwi; v- prędkość krwi
Podstawiając f2 do wzoru na f1:
gdy się oddala od głowicy `-' a gdy przybliża `+'
267. Wytwarzanie i detekcja USG
Przetworniki piezoelektryczne służą do rejestrowania i wytwarzania ultradźwięków do celów medycznych. Wykorzystuje się w nich zjawisko piezoelektryczne i jego odwrócenie.
Zjawisko to występuje w anizotropowych kryształach dielektrycznych np. kwarc. (patrz wyżej- zjawisko piezoelektryczne )
Jeśli częstotliwość drgań płytki będzie wynosiła 17kHz- 1GHz wówczas płytka wytwarza ultradźwięki.
Drgające przetworniki piezoelektryczne przyłożone do ośrodka biologicznego przekazują mu drgania. Jest to wtedy generator ultradźwięków.
Jeżeli od ośrodka biologicznego drgania dojdą do przetwornika piezoelektrycznego to wytworzone w nim zmienne napięcie elektryczne. Jest to wtedy detektor ultradźwięków.
METODA FALI CIĄGŁEJ: pierwszy przetwornik wytwarza ultradźwięki (przetwornik nadawczy), a drugi służy do odbioru ultradźwięków (przetwornik odbiorczy).
METODA IMPULSOWA: przetwornik wytwarza bardzo krótkie fale ultradźwięków, a w przerwie ich wytwarzania je odbiera, a więc zarówno jest detektorem i generatorem.
Przetworniki znajdują się wewnątrz głowicy piezoelektrycznej.
268. Charakterystyka fal USG (?)
W ultrasonografii wykorzystuje się fale ultradźwiękowe. Są to fale akustyczne (mechaniczne), których częstotliwość zawiera się w zakresie 17kHz - 1 GHz (powyżej hiperdźwięki).
269. Zjawisko tłumienia w USG
Zjawisko tłumienia uniemożliwia otrzymanie dowolnie dużych częstotliwości f dla otrzymania dużej zdolności rozdzielczej.
p (d)= p0 × e-αd
p- ciśnienie akustyczne na głębokości d
p0 - cisnienie akustyczne początkowe
α -współczynnik tłumienia
d- głębokość wnikania
Za tłumienie ultradźwięków w tkankach odpowiedzialne są 2 zjawiska:
Im większa częstotliwość ultradźwięków tym absorpcja jest silniejsza
α a ~ f αa - współczynnik absorpcji
W zależności od wielkości ośrodka rozpraszania wyróżniamy 2 rodzaje rozpraszania ultradźwięków:
a) rozpraszanie Rayleigha - zachodzi gdy długość ultradźwięków jest dużo większa od wielkości struktur rozpraszających np.-. rozpraszanie ultradźwięków na erytrocytach, trombocytach
αR = kR ×f4 αR- współczynnik rozpraszania Rayleigha
b) rozpraszanie Tyndalla- zachodzi gdy długość ultradźwięków jest porównywalna do wielkości struktur rozpraszających ( wielkości tego samego rzędu) wystepuje zazwyczaj na granicy dwóch różnych tkanek
αT = kT × f 2 αT- współczynnik rozpraszania tyndalla
Wzrost częstotliwości powoduje wzrost współczynnika rozpraszania. α= αa+ αr
α współczynnik tłumienia
αa- współczynnik absorpcji
αr- współczynnik rozpraszania
270. zdolność rozdzielcza USG
Jest to odwrotność odległoścdmin między dwoma punktami które można oddzielić w danej metodzie( można je zobaczyć).
Z= 1/ dmin~1/λ~f
Zdolność rozdzielcza powinna być jak największa, czyli odległość między dwoma punktami powinna być jak najmniejsza.
Zdolność rozdzielcza jest rzędu długości fali używanej w danej metodzie. Jest odwrotnie proporcjonalna do długości fali i wprost proporcjonalna do częstotliwości fali.
271. Echa USG
Fala ultradźwiękowa wnikając do organizmu i trafiając na przeszkodę w postaci krwi lub tkanki tłuszczowej (których współczynniki odbicia są większe od zera) ulega częściowemu odbiciu i wraca do aparatu USG w postaci echa. Echo niesie ze sobą informację o granicy dwóch tkanek.
Im dalej jest granica dwóch tkanek od głowicy tym amplituda powracających ech jest mniejsza co jest tłumaczone efektem tłumienia. Na podstawie czasupowrotu echa otrzymuje sie informacje o odległości granicy tkanek od głowicy piezoelektrycznej. Echa przedstawiane są w prezentacjach A, M, 2D.
Zależność odległości granicy tkanek od głowicy przedstawia równanie:
2x=ct, gdzie c to szybkość rozchodzenia się ultradźwięku w tkance.
Więc x=ct/2
272. Wzmocnienie USG
W badaniu USG otrzymujemy szereg ech ultrasonograficznych. Ze względu na tłumienie ultradźw. amplituda ech jest coraz mniejsza. Do wzmocznienia ultradżwięków wykorzystujemy metodę SRW - strefowej regulacji wzmocnienia im później echo dociera do głowicy piezoelektrycznej tym jest silniej wzmacniane. Dzięki temu dochodzi do wyrównania amplitudy ech.
275. Czynniki wpływające na rozchodzenie się fal ultradźwiękowych
c=
gdzie: k- współrzędna sprężystości ośrodka
Dla kości i mięśni prędkości te zależą również od kierunku fali, bo są to ośrodki anizotropowe.
Przykładowe prędkości: w powietrzu- 340m/s, w tk. miękkich- ok.1500m/s, w kościach- 4000m/s
Długość fali zależy od prędkości rozchodzenia się: (f- częstotoliwość)
=
Zdolność rozdzielcza jest proporcjonalna do częstotliwości i odwrotnie proporcjonalna do długości fali.
276. Prezentacja A
-(amplitudowa, askopia)
-wykorzystywana w okulistyce
-polega na analizie amplitud powracających ech
-do uzyskania obrazów wystarczy głowica USG z pojedynczym kryształem piezoelektrycznym
277 prezentacja m
Prezentacja M (Motion, ruch) jest jednym ze sposób w echografii przedstawienia informacji o granicach tkanek w sercu. W prezentacji M cała podstawa głębokości porusza się ruchem jednostajnym. W metodzie tej stosuje się ekrany z długą poświatą, które długo utrzymują obraz, dzięki czemu można go sfotografować. Dzięki znajomości prędkości przemieszczania się głębokości podstawy można wyliczyć takie parametry serca jak: szybkość drgań m. sercowego oraz zastawek.
278 ilościowa metoda pomiaru prędkości krwi w Dopplerze
Ilościowa metoda pomiaru prędkości krwi jest możliwa, gdy znamy kąt Θ, czyli położenie naczynia krwionośnego. (Jeśli nie znamy to JAKOŚCIOWA metoda.)
W wykładach jest taki schematyczny rysunek do tego.
Mamy 2 pary głowic piezoelektrycznych, przełącznik i analizator. Przełącznik najpierw pozwala na pracę jednej głowicy. Wysłana fala odbija się i powraca. Analizator rejestruje częstotliwość fal dla 1-szej pary generatorów:
Po zanalizowaniu czestoliwości z pierwszego generatora, przełącznik wyłacza go i pozwala na pracę drugiemu generatorowi, który wysyła fale o tej samej częstotliwości. Fale powracają i analizator rejestruje częstotliwość fd2
Po porównaniu fd1 do fd2 i przekształceniach wychodzi:
Fd1,fd2->częstoliwość dopplerowska
Kąt Θ-> położenie naczynia krwionośnego.
279. Częstotliwość dopplerowska - jest charakterystyczna m.in. dla fal elektromagnetycznych i dźwiękowych, zjawisko to polega na pozornej zmianie częstotliwości źródła fal, wynikającej z ruchu źródła albo z ruchu obserwatora.
Ruch badanego obiektu w kierunku głowicy powoduje wzrost częstotliwości fali odbitej, natomiast ruch "od" głowicy powoduje spadek częstotliwości fali odbitej.
1) Ruchome źródło, obserwator nieruchomy
a) źródło zbliża się z pewną prędkością do obserwatora. Obserwator odbierze wyższą niż emitowaną częstotliwość
f1= f0 c/c-v
b) źródło oddala się z pewną prędkością do obserwatora. Obserwator odbierze niższą niż emitowaną częstotliwość
f1= f0 c/c+v
2) Nieruchome źródło, obserwator ruchomy
a) obserwator zbliża się z pewną prędkością do obserwatora (v)
f2= f0 c+v/c
b) obserwator oddala się z pewną prędkością do obserwatora (v)
f2= f0 c-v/c
Zjawisko Dopplera zostało wykorzystane w diagnostyce układu krążenia, do wyznaczania średniej prędkości krwi, rozkładu prędkości krwi w naczyniach, głownie dla dużych naczyń klatki piersiowej i większych tętnic obwodowych.
280. Impulsowa metoda dopplerowska.
Znajomość prędkości krwi otrzymanej za pomocą metody fali ciągłej ultrasonografii nie jest wystarczająca. Monitorowanie rekonwalescencji wymaga często oznaczenia wydatku krwi w naczyniu krwionośnym.
Ten właśnie WYDATEK można wyznaczyć METODĄ IMPULSOWĄ ULTRASONOGRAFII DOPPLEROWSKIEJ.
Strumień krwi: wydatek
Q=ΔV/Δt=lS/Δt=Vśrπr2
Q= VśrΠr2
→ trzeba zmierzyć Vśr i promień naczynia r
Na granicy z naczyniem część fal ulega odbiciu - pierwsze echo, część wchodzi odbija się od warstw krwi, część odbija się od drugiej ścianki - drugie echo.
Mierzy się czas I i II echa:
d= ct → r= 1/2 ct gdzie c prędkość, t czas
2r=cτ → r=1/2cτ τ - średni czas między echami
Z powyższych mamy promień. Możemy wyliczyć wydatek czyli ilość krwi przepływającą w danym czasie.
282 Dlaczego zanika sygnał NMR?
-Wynika to z wzoru na moment pędu μ=-e/T*πr^2 gdzie czas jest w mianowniku więc z jego wzrostem zmniejsza się wartość moment pędu od której zaś zależy NMR
283.
Częstość Larmora (fL) częstość z jaką jądra precesują wokół własnej osi
fL=1/2π*γ*Bo
284
Obrazowanie NMR
Jeżeli zewnętrzne pole magnetyczne jest niejednorodne (istnieje gradient pola), to częstość rezonansowa będzie zależała od współrzędnej położenia jądra w próbce. Obserwując natężenie sygnału w zależności od głebokości można uzyskać przestrzenny rozkład atomów danego pierwiastka.
Stosując gradient kolejno w kierunkach osi x, y i z otrzymuje się pełny, 3-wymiarowy obraz badanego ciała.
Indukcja pola magnetycznego w położeniach x1 i x2 jest różna
źródło informacji to sygnału magnetycznego rezonansu jądrowego
• badany obiekt umieszczany jest w zewnętrznym silnym polu magnetycznym Boi oświetlany falą elektromagnetyczną o częstości ω= γBo, odpowiadającą częstości precesyjnej Larmora obserwowanych jąder
• ze względu na wysoką koncentrację w materii biologicznej i duży współczynnik giromagnetyczny najczęściej są to jądra 1H.
•na jednorodne pole magnetyczne nakładany jest liniowy gradient pola G -różnicuje to zatem częstość rezonansu jąder w poszczególnych komórkach analizowanego obiektu (vokselach)
Obrazowanie -metoda projekcji. Gradienty pola podawane pod różnymi kątami względem pola Bo pozwalaj ąna otrzymywanie zbiorczych sygnałów od odpowiednich warstw ciała. Procedura komputerowa pozwala na otrzymanie z nich obrazów przestrzennych (podobnie jak w tomografii rentgenowskiej)
Gradient magnetyczny NMR
Niezerowy spin jądrowy posiadają praktycznie wszystkie atomy. W bardzo dużym uproszczeniu spin jądrowy można sobie wyobrazić jako rotowanie jądra wokół własnej osi. Jest on związany z wewnętrznym momentem pędu jądra. Każde jądro jest obdarzone dodatnim ładunkiem elektrycznym, stąd jego spin generuje bardzo słabe pole magnetyczne i jest źródłem momentu magnetycznego.
Podstawą zjawiska NMR jest oddziaływanie spinów jądrowych z polami magnetycznymi:
285. Zależność nmr od czasu. (nie wiem czy na pewno tak należy odpowiedzieć ale nic innego nie wymysle. może chodzi o czasy T1 i T2 ale to jest w innych pytaniach, osłabienie sygnału też jest w osobnym pytaniu. najwyraźniej niektóre pytania się w jakimś stopniu pokrywają)
Po wyłączeniu impulsu fali radiowej RF zaburzony układ recesujących jąder wraca do stanu równowagi - rośnie wartość namagnesowania podłużnego Mz a maleje do 0 namagnesowanie poprzeczne Mxy i indukuje ono na cewce odbiorczej napiecie - sygnał FID/prąd indukcyjny SEM/.
Sygnał ma malejącą w czasie amplitudę. Spowodowane to jest przez sąsiednie jądra. wytwarzają one pola magnetyczne które są różne gdyż jądra te precesują z różnymi czestotliwościami, z różnymi prędkościami i następuje rozfazowanie które osłabia sygnał.
Sygnał bezpośrednio odbierany jest jako widmo w domenie czasu (U=f(t)) i następnie komputer dokonuje przekształcenia Fouriera i otrzymuje się sygnał NMR jako widmo w domenie częstości (A=f(f)) który dopiero teraz jest użyteczny w diagnostyce medycznej.
286
Pole radiowe NMR
Po umieszczeniu pacjenta w magnesie, generowana jest fala radiowa o częstotliwości radiowej, takiej samej jak częstotliwość precesji. Działanie impulsu RF jest krótkotrwałe. Fala radiowa zwana impulsem RF (RF - ang. Radio Frequency) ma na celu wywołanie zakłócenia w precesji protonów. Tylko wówczas będzie możliwa wymiana energii impulsu RF z protonami. Wymiana energii między protonami i impulsem RF to właśnie zjawisko rezonansu. W najprostszym ujęciu - rezonans zachodzi wówczas, gdy protony wirują z częstotliwością podawaną przez impuls RF.
Przez odpowiedni wybór częstotliwości radiowych możemy zmusić do precesji tylko jeden, wybrany rodzaj jądra.
Moment magnetyczności można obrócić o dowolny kąt α radiowym sygnałem α-stopniowym. Jeżeli wektor M obróci się o 90®, to znaczy, że do próbki został podłączony sygnał radiowy 90®
Wektor magnetyczności wykonuje ruch precesyjny wokół kierunku pola radiowego - pole radiowe wyznacza kierunek, wokół którego wektor magnetyzacji wykonuje ruch precesyjny.
Precesja pola radiowego: fl,r=(1/2π)γB1=1/Tr (B1 - pole radiowe, γ - czynnik giromagnetyczny)
W czasie 1/Tr wektor magnetyzacji wykona ruch o kąt 180®
360®/Tr=α/t
Gdzie: t - czas pola radiowego
α=(t*360®)/Tr=(360®/2π)γB1t
Regulując czas pola radiowego, możemy regulować α
Wirujące (precesujące) jądra wytwarzają pole magnetyczne. W cewce odbiorczej (cienki drucik miedziany o maleńkim oporze) powstanie prąd indukcyjny. Ta powstająca siła elektromotoryczna nazywa się sygnałem Enemerowskim.
287. Fala Radiowa NMR
Gdy umieścimy obiekt w magnesie, generowana jest fala radiowa o częstotliwości radiowej, takiej samej jak częstotliwość precesji.
Fale radiowe są falami niejonizującymi. Ich częstotliwość jest znacznie mniejsza od częstotliwości fal rentgenowskich, o energiach mniejszych od fal światła widzialnego. Jest to promieniowanie o niskiej energii, dlatego też bezpieczne.
(na pionowej osi w górę M₀, poziomej M₁ a w dół M₂)
Przez odpowiedni dobór fal radiowych możemy zmusić do precesji tylko jeden wybrany rodzaj jądra atomowego. Po włączeniu pola radiowego wektor M dchyla się od osi Z' wokół osi Y'(na wykresie lina okrągła ) Podłączony impuls może być dowolny np. 90 albo 180 stopni.
289.Zjawisko Zeemana -
rozszczepienie poziomów energetycznych atomu (cząsteczki) pod wpływem zewnętrznego pola magnetycznego, w wyniku którego obserwuje się rozszczepienie linii widmowych emitowanego przez ten atom (cząsteczkę) promieniowania; odkryte zostało w widmie promieniowania sodu przez Petera Zeemana.
Zjawisko Zeemana normalne występuje dla linii singletowych; przy obserwacji w kierunku prostopadłym do linii sił pola magnetycznego każda linia widmowa rozszczepia się na 3 linie składowe (zjawisko Zeemana poprzeczne- wówczas światło tych linii jest spolaryzowane pionowo), a przy obserwacji w kierunku równoległego do linii sił pola — na 2 składowe (światło linii spolaryzowane pionowo).
gdzie:
mJ - liczba kwantowa rzutu momentu magnetycznego,
B - indukcja magnetyczna,
Zjawisko Zeemana anormalne występuje dla linii multipletowych i polega na rozszczepieniu każdej linii widmowej na wiele składowych. Rozszczepienie jest niewielkie i nawet w silnych polach magnetycznychjego obserwacja wymaga stosowania spektrometrów interferencyjnych jak na przykład interferometr. Wyjaśnienie tego zjawiska daje kwantowa teoria atomu (skwantowanieenergii oddziaływania momentów magnetycznych elektronów na zewnętrzne pole magnetyczne)
290- 291.
Czas relaksacji T1
Relaksacja- bezpromieniste przekazanie nadmiaru energii spinów do otoczenia.
Czas relaksacji T1(podłużnej), to powrót składowej do stanu wyjściowego, wynika z oddziaływania spin-sieć. Stanowi czas, po którym wartości składowych osiągną zmiane 63% ich wartości maksymalnej.
Mz(f)= Moz (1-e^t/T1)
Gdzie:
Moz- poczatkowa wartość magnetyzacji
Mz-wektor magnetyzacji względem osi Z
t-czas
T1- czas relaksacji podłużnej
Jest to czas, po którym układ dochodzi do równowagi termicznej pomiedzy układem spinow a siecia-otoczeniem. ( ciecz- kilka sekund, ciala stale-kilka godzin)
Zjawisko to wykorzystuje się w tomografii NMR-owskiej, gdzie uzyskujemy obraz, podający rozklad czasu relaksacji (odpowiednim czasom przyporzadkowuje się określone kolory)
Czas relaksacji T2(poprzecznej)
Powrót składowej Mx,z do zera, wynikajaca z oddziaływania spin-spin. Stanowi czas, po którym wartości składowych osiągną zmiane 63% ich wartości maksymalnej.
Gdy do probki przyłożymy impuls 90º wektor M zacznie wirowac w płaszczyźnie XY . Od tych wirujących jader wytwarza się pole magnetyczne w płaszczyźnie XY. Cewka zbiorcza znajduje się w polu magnetycznym. Powstaje w nim prad indukcyjny SEM- sygnał NMR
SEM=μo e^-t/T2
Gdzie:
μo- poczatkowa wartość magnetyzacji
t-czas
T2- czas relaksacji poprzecznej
Dla cieczy (występują ruchy Browna)-pola magnetyczne sąsiednich jader sie zeruja. T2 kilka sekund
Ciała stałe( pola magnetyczne sąsiednich jader sie nie zeruja) T2 rzedu milisekund
Zjawisko to wykorzystuje się w tomografii NMR-owskiej, gdzie uzyskujemy obraz, podający rozklad czasu relaksacji (odpowiednim czasom przyporzadkowuje się określone kolory)
292. Generacje CAT
Tomografy I generacji
a ) Stosuje się matrycę 256×256 1 pixel = 1mm
1024×1024 1 pixel = 0,1mm
b) W zależności od ilości pól mamy różną rozdzielczość. W tomografii komputerowej przyjmujemy, że voxel jest strukturą niejednorodną, nie rozpatrujemy jego budowy.
c) Zdjęcie otrzymane w TK (tomogram) jest obrazem rozkładu współczynnika absorpcji dla różnych voxeli. Wartościom współczynnika absorpcji przyporządkowuje się różne odcienie szarości, czerni i bieli.
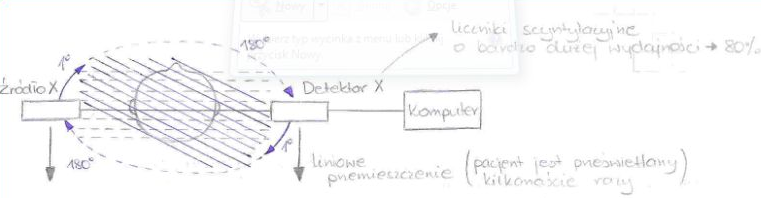
d) Czas wykonywania zdjęcia 5 min (ze wzgl na obroty i rotację przyrządów)
Tomografy II generacji
a) Czas wykonania zdjęcia ok. 20s
b) Źródła promieniowania wytwarzają wiązkę wachlarzowatą. Promieniowanie pada na układ detektorów. Przesunięcie liniowe układu źródło-detektory . Potem obrót układu o 10˚. Kolejne przesunięcia i obroty.
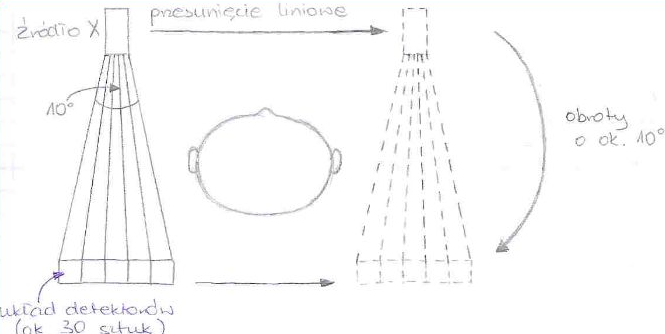
Tomografy III generacji
a) Czas wykonania zdjęcia ok. 3s
b) Likwidacja przesunięcia liniowego
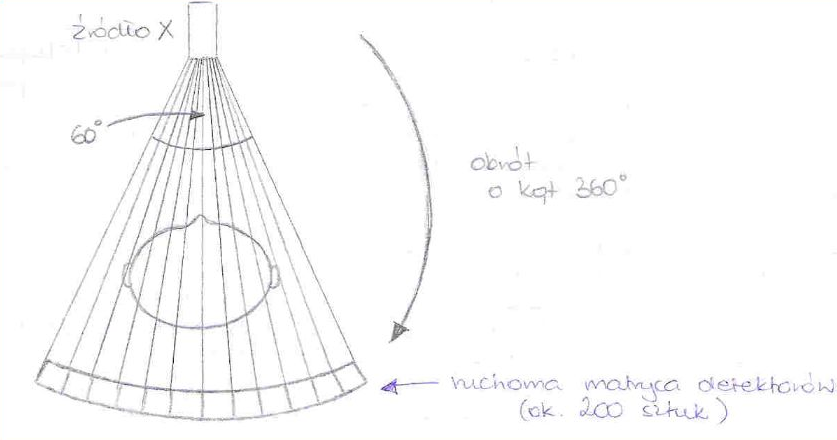
c) Układ źródło-matryca obraca się o 360˚ wokół pacjenta.
Tomografy IV generacji
a) Czas wykonania zdjęcia 1s
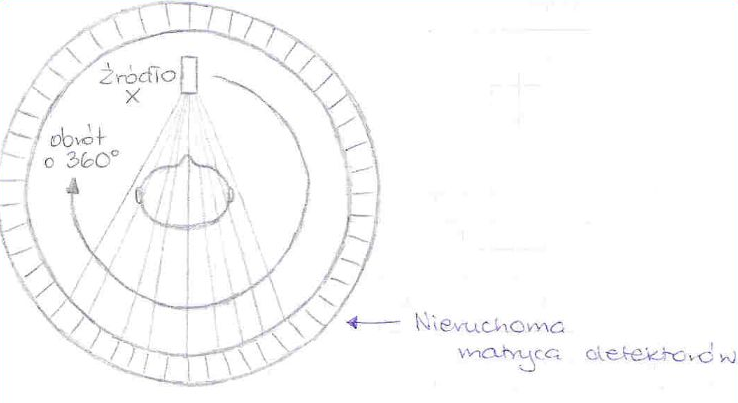
Tomografia spiralna - jednostajne wsuwanie stolika z pacjentem do wnętrza tomografu - możliwe ciągłe wykonywanie zdjęć.
293. CAT - wady i zalety
ZALETY |
WADY |
duża czułość zdjęć - obserwujemy obszary różniące się absorpcją o 0,5% : widać np. istotę białą i szarą mózgu, skrzepy krwi, płyny ustrojowe |
każda dawka promieniowania jonizującego jest niebezpieczna |
możliwość rekonstrukcji przestrzennej obrazu |
dąży się do skrócenia czasu naświetlania |
294 Współczynnik osłabienia CAT
Współczynnik osłabienia CAT, zakładam że chodzi o wsół. Absorpcji, bo to chyba to samo.
W tomografii komputerowej, w której analiza ilościowa opiera się na pomiarze natężenia wykorzystuje się współ. osłabienia.
Nateżenie promieniowana po przejściu przez układ vokseli jest równe:
Wprowadza się tzw PREZENTACJE- P.
( wzory macie w wykladach)
Znajomosc tych prezentacji pozwala na obliczenie współczynnikow osłabiania.
W rzeczywistym obrazie, róznym współczynnikom osłabiania przyporządkowuje się rozne szarości. Stopień szarości określa liczba CT , czyli jednostka Hausfielda HV:
(wzor w wykladach)
Dla powietrza HV= - 1000 i obraz jest dokladnie czarny
Dla kosci HV= 3000 i wtedy mamy wszystkie odcienie kolorow.
W praktyce stosuje się obrazy o odnienieach od 0 do 256.
→
Mz
Wyszukiwarka
Podobne podstrony:
Bank pytan (lekarski) id 79351 Nieznany (2)
Bank pytań biochemia stoma i lek
Bank pytan teoretyczny egzamin dyplomowy
bank pytań
bank pytań, ŚUM, anatomia, banki pytań
BANK PYTAŃ TESTOWYCH, kosmetyka
bank pytań z fizjo
Bank pytan fizjologia 08 opracowane
bank pytan neurologia dziecieca, fizjoterapia w pediatrii
bank pytan kardiologia(1), Nauka, Medycyna, Kardiologia
Bank pytan z anatomii, 1
Bank pytan testowych z tabelka odpowiedzi
OTO PRZED TOBĄ BANK PYTAŃ STWORZONY SIŁĄ WIELU OS, Immunologia, inne
Bank pytan fizjo macio p
BANK PYTAŃ TESTOWYC2, kosmetyka
ET EGZAMIN BANK PYTAŃ, SGGW TRiL, ET Tril sggw Eksploatacja techniczna
bank pytań z fizjo, II ROK STOMATOLOGIA SUM ZABRZE, FIZJOLOGIA, FIZJOLOGIA EGZAMIN, foldery z pytani
więcej podobnych podstron