Postać ostateczna transmitancji obiektu:

Postacie transmitancji podrzędnych wynikają z poniższego wzoru.

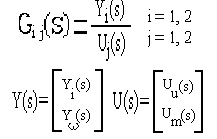
Macierz transmitancji.

- wymuszeniowa: prądowa G_{I U} = ^I(s) / _U(s) - zakłóceniowa: prądowa G_{I M} = ^I(s) / _M(s)

prędkość. G_ωU = ^ω(s) / _U(s) prędkość. G_ωM = ^ω(s) / _M(s)

4.Postacie numeryczne.

Dane : R = 0,8Ω L = 0,04 H n _N =1100 obr / min I_N = 100 A U_N =220V J = 2,5kgm²

Z tych danych można policzyć k.

K = (U_N -I_NR) / ω_N ...(14)

ω_N = 2*π*f

f=1100 obr / 60 sek

f=18,33..(3) Hz

Można przyjąć, że f =18,33 Hz, więc ω_N = 115 s^-1

Po podstawieniu do (14) K=1,22 [V*s]

oraz Mn=K*I =122[V*s*A]

a)

b)

c) Wyznaczenie G(s) na podstawie matlaba.

Korzystam z funkcji [N,E]=ss2tf(A,B,C,D,iu), gdzie iu to numer wejścia, A, B, C ,D macierze stanu, macierz E zawiera współczynniki mianownika, macierz N zawiera współczynniki licznika.

Postać programu:

A=[-30.5,-20;0,0.49]

B=[25,0;0,-0.4]

C=[1,0;0,1]

D=[0,0;0,0]

[N1,E1]=ss2tf(A,B,C,D,1)

[N2,E2]=ss2tf(A,B,C,D,2)

***********************

G_{I U} = 0

G_{I M} = (0s² + 0.4000s-12.2000)/(1s²+30.0100s -14.9450)

G_ωU = (0s² + 25s-12.2500) /(1s² + 30.0100s -14.9450)

G_ωM = (0s² + 0s -+8) / (1s² + 30.0100s -14.9450)

Widać, że te wyniki policzone prez Matlaba są identyczne jak policzone ręcznie.

5. Odpowiedź układu na skok jednostkowy na podstawie matlaba.

Polecenie step(A,B,C,D) umożliwia wygenerowanie odpowiedzi układu na skok jednostkowy.

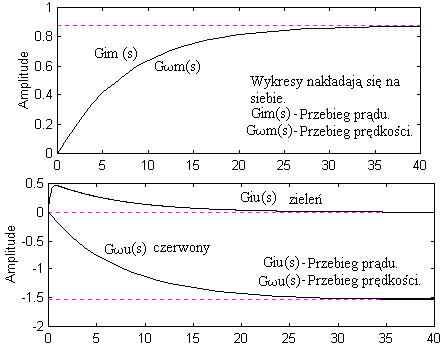
6. Wykresy w jedym oknie:

1. W pierwszym oknie jest odpowiedź na M(s) =s^-1 czyli przebiegi G_{I U} G_ωU.

2. 
   W drugim oknie jest odpowiedź na U(s) = s^-1 czyli przebiegi G_IM G_ωM.

2

---