Wydział Nauki o żywności Olsztyn, 18.05.2009r.

Kierunek: Technologia żywności i żywienie człowieka

Sprawozdanie nr 43

Temat: Pomiar współczynnika załamania światła oraz wyznaczenie stężenia roztworów metodą refraktometryczną.

Część teoretyczna:

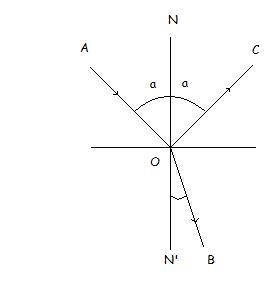
Zazwyczaj przy padaniu światła na granicę dwóch ośrodków przezroczystych, różniących się prędkością rozchodzenia się światła, część energii promienistej przechodzi do drugiego ośrodka w postaci promienia załamanego. Załamanie światła na granicy dwóch ośrodków izotropowych polega następującym prawom:

1. Kąt padania
   i kąt załamania
   leżą w jednej płaszczyźnie. Kąt załamania jest to kąt utworzony przez normalną ON' i promień załamany OB.

2. Stosunek sinusa kąta padania do sinusa kąta załamania równa się stosunkowi prędkości
   rozchodzenia się światła w ośrodku pierwszym do prędkości
   rozchodzenia się światła w ośrodku drugim. Jest to wielkość stała dla danych dwóch ośrodków i danego rodzaju promieniowania

Wielkość
nazywamy współczynnikiem załamania ośrodka drugiego względem pierwszego. Wprowadzamy też pojęcie bezwzględnego współczynnika załamania. Jest to współczynnik załamania danego ośrodka względem próżni. W próżni wszystkie rodzaje promieniowania rozchodzą się z tą samą prędkością. Prędkość tę wyznaczano różnymi metodami. Parę podstawowych metod omówimy w następnym paragrafie.

Oznaczamy bezwzględne współczynniki załamania dwóch ośrodków, np. ośrodka A i ośrodka B, przez
:

Skąd względny współczynnik załamania ośrodka B względem A (przejście promienia z A do B)

Zjawisko całkowitego wewnętrznego odbicia:

Rozważmy przejście promienia z ośrodka B o mniejszej prędkości rozchodzenia się światła do ośrodka A o prędkości większej.

Promień padający I pada pod kątem
, załamuje się pod kątem
, a równocześnie częściowo się odbija. Kąt
, ponieważ
. Promień II pada pod kątem
, załamuje się pod kątem
, większym od
. Dalszy promień III może padać pod takim kątem
, któremu odpowiada kąt załamania
równy 90
. Jeśli jeszcze bardziej powiększymy kąt padania promienia, to już nie otrzymamy promienia załamanego: cała energia promienia padającego przypadnie na promień odbity. W tych warunkach mówimy o zjawisku całkowitego wewnętrznego odbicia.

Ustalamy warunki, jakie muszą być spełnione, aby mogło wystąpić zjawisko całkowitego wewnętrznego odbicia. Przede wszystkim promień musi przechodzić z ośrodka B o mniejszej prędkości rozchodzenia się światła (czyli z ośrodka optycznie gęstszego) do ośrodka A o prędkości większej (optycznie rzadszego). Poza tym kąt padania promienia musi być większy od tzw. kąta granicznego. Przez kąt graniczny rozumiemy taki kąt padania, któremu odpowiada kąt załamania równy 90
. Kąt ten spełnia równanie:

Gdzie
są odpowiednio bezwzględnymi współczynnikami załamania ośrodka optycznie rzadszego A i gęstszego B.

Część praktyczna:

Tabela1.

Pomiar numer			W radianach					W radianach
1			0,331607	0,191983	1,706252308			1,63504954
2			0,628308	0,34906	1,718571822
3			0,733026	0,418872	1,645123543
4			1,082086	0,593402	1,578975863
5			1,22171	0,663214	1,526324164
6							41	0,715573	1,524274117

Niepewność pomiarowa:

Tabela2:

Lp.	n		C
Woda	1,3332		-
1	1,3379		3,4%
2	1,3445		7,9%
3	1,3509		11,9%
4	1,3559		15%
5	1,3643		20,4%
Temp. pomiaru

---