data.28.10.2002

Dzień.tyg. poniedziałek

WYDZIAŁ INŻYNIERII PRODUKCJI Godzina 14⁰⁰-17⁰⁰

Kierunek ZIP grupa 7

Ćwiczenie nr. 64

Temat: Wyznaczanie zależności współczynnika załamania światła od stężenia roztworu za pomocą refraktometru Abbego.

Cel ćwiczenia :

Celem tego ćwiczenia jest pomiar zależności współczynnika załamania światła od stężenia roztworów w naszym przypadku badany będzie roztwór gliceryny. Do pomiaru współczynnika załamania cieczy został wykorzystany refraktometr Abbego.

Wstęp teoretyczny :

Prawa dotyczące odbicia i załamania światła:

Przy omawianiu oddziaływania światła z różnymi obiektami można pojęcie promienia świetlnego jeśli pominiemy korpuskularno - falową jego naturę. Promień świetlny to po prostu bardzo wąska wiązka światła, której oś wyznacza kierunek rozchodzenia się energii świetlnej. Bieg promieni po przezroczystym ośrodku można określić opierając się na podstawowym założeniu optyki geometrycznej, że światło w ośrodku jednorodnym i izotropowym rozchodzi się wzdłuż linii prostych, a przecinające się wiązki światła nie oddziaływują ze sobą . Trzeba jednak pominąć możliwość ugięcia lub interferencji światła.

Zachowanie się promieni świetlnych na granicy dwóch ośrodków opisują prawa odbicia i załamania światła. Prawa te choć początkowo istniejące w fazie doświadczalnej łatwo jest udowodnić w praktyce. Gdy wiązka światła trafia na swej drodze na inne środowisko , to na powierzchni granicznej część promieniowania zostaje odbita, rozproszona lub pochłonięta, a reszta przechodzi dalej ulegając załamaniu.

Prawa dotyczące odbicia i załamania są następujące.

1. promień padający, odbity i załamany oraz normalna do powierzchni granicznej leżą w jednej płaszczyżnie.

2. kąt padania α₁ jest równy kątowi odbicia α₁` : α<sub>1</sub>=α<sub>1</sub>`

3. stosunek sinusa kąta padania α₁ do sinusa kąta załamania α₂ jest wielkością stałą :

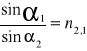
gdzie n_2,1 jest współczynnikiem załamania ośrodka 2 względem ośrodka 1, z którego wychodzi.

Współczynnik załamania wyraża się dodatkowo stosunkiem prędkości w obu ośrodkach

n_2,1 = v₁/v₂

v₁ - prędkość światła w ośrodku 1, v₂ - prędkość w ośrodku 2.

Współczynnik załamania światła w próżni nosi nazwę bezwzględnego współczynnika załamania n,

n = c/v

c - prędkość światła w próżni, v - danym ośrodku. Bezwzględny współczynnik załamania ośrodka w praktyce można posługiwać się wsp. załamania danego ośrodka względem powietrza ponieważ wsp. względem powietrza różni się bardzo niewiele od wsp,. w próżni. Przekształcając wzór otrzymamy :

n_2,1 =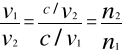

czyli względny współczynnik załamania n_2,1 dwóch sąsiadujących ze sobą ośrodków równy jest stosunkowi bezwzględnych współczynników załamania tych ośrodków.

Dużo prostszy sposób wyznaczania współczynnika załamania ośrodka oparty jest na zjawisku całkowitego wewnętrznego odbicia światła.

Całkowite wewnętrzne odbicie

Ma ono miejsce wówczas, gdy promień świetlny biegnie ze środowiska optycznie gęstszego 2 do rzadszego 1pod kątem większym od tzw. kąta granicznego. Światło przechodząc z ośrodka 2 do 1 ulega załamaniu od normalnej , czyli kąt załamania jest większy od kąta padania. W tym przypadku musi więc istnieć taki kąt graniczny padania α_g , przy którym kąt załamania równy jest π/2 i wówczas promień załamany biegnie równolegle do granicy dwóch ośrodków. Przy kątach α
α_g promienia załamanego nie obserwuje się w ogóle. Jest to całkowite wewnętrzne odbicie, ponieważ w promieniu odbitym zawiera się całkowita energia promienia padającego. Z prawa załamania światła wynika, że w przypadku przejścia światła z ośrodka 2 do 1 możemy napisać :

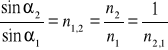
Wartość kąta granicznego α_g= α₂ określona jest przez warunek , aby kąt załamania α₁ w ośrodku 1 spełniał α₁ = π/2, skąd na podstawie wcześniejszego wzoru otrzymujemy :

n_2,1 =

Zasada działania refraktometru Abbego.

Zasadniczą częścią działania refraktometru Abbego są dwa prostokątne pryzmaty - oświetlający P₁ i pomiarowy P₂, wykonane ze szkła o dużym współczynniku załamania (szkło flintowe). Pryzmat P₁ może obracać się wokół osi O₁. Miedzy te pryzmaty wprowadzamy kilka kropel badanej cieczy, której współczynnik załamania powinien być mniejszy niż współczynnik załamania szkła pryzmatów. Ciecz tworzy między przeciwprostokątnymi powierzchniami pryzmatów cienką, płasko-równoległą warstewkę. Do oświetlenia pryzmatu P₁

Stosuje się światło białe rozproszone. Pada ono pod różnymi kątami na powierzchnię graniczną między pryzmatem P₁, a warstewką cieczy. Do cieczy przechodzą tylko promienie padające pod katem mniejszym od kąta granicznego. Promienie, które przechodzą dalej biegną przez pryzmat P₂, doznając w warstwie cieczy niewielkiego równoległego przesunięcia. Pryzmat P₃, zwany kierującym, zmienia kierunek promieni przechodzących, które docierają do lunetki L przez układ pryzmatów Amiciego P₄ i P₅. W wyniku zjawiska wewnętrznego odbicia na przeciwprostokątnej powierzchni pryzmatu P₁, część pola widzenia w lunetce jest oświetlona, a część pozostaje ciemna. Linię odgraniczającą część oświetloną od zaciemnionej możemy przesuwać w górę i w dół obracając pryzmat P₃ wokół osi O₂ - do pomiaru ustawiamy ją na przecięciu nici pajęczych okularu lunety L. Z pryzmatem P₃ połączona jest podziałka, na której odczytujemy wartość kąta granicznego lub bezpośrednio współczynnik załamania cieczy- podziałkę tę obserwujemy w dodatkowej lunetce.

W pryzmatach refraktometru jak i w badanej cieczy występuje zjawisko dyspersji czyli rozszczepienia światła białego. W wyniku tego zjawiska, linia rozgraniczająca pole widzenia nie jest ostra lecz barwna i rozmyta. W refraktometrze Abbego rozszczepienie jest skompensowane przy użyciu dwóch układów pryzmatów P₄ i P₅ wykonanych z kilku pojedynczych pryzmatów z różnych gatunków szkła. Kąty łamiące poszczególnych pryzmatów są tak dobrane, że światło żółtej linii sodu nie ulega żadnemu odchyleniu, a odchyleń przeciwnych kierunkach doznają promienie czerwone fioletowe. Przez względny obrót pryzmatów kompensatora można zlikwidować zabarwienie linii podziału.

Przeprowadzenie doświadczenia:

• Przed przystąpieniem do wykonania doświadczenia trzeba wykonać kilka czynności przygotowujących. Odkręcamy zakrętkę zawierającą pryzmaty pomiarowe P₁ i P₂ refraktometru i przemywamy powierzchnie wodą destylowaną poczym wycieramy bibułką. Wprowadzamy badaną ciecz na powierzchnię pryzmatu tak aby pokryła całą jego matową powierzchnię i zamykamy pryzmaty.

• Włączamy lampkę i przy użyciu lusterka refraktometru kierujemy światło na oba pryzmaty aby trafiało do lunetki obserwacyjnej L.

• Przekręcamy pokrętło aż do ujrzenia lini rozgraniczającej pola jasne i ciemne.

• Nastawiamy okular lunetki L tak, aby zobaczyć ostry obraz krzyża z nitek pajęczych i wyrażną linię rozgraniczającą pola jasne i ciemne.

• Ustawiamy położenie linii granicznej na skrzyżowaniu nici pajęczych.

• Odczytujemy na dodatkowej lunetce , bezwzględny współczynnik załamania badanej cieczy. Powtarzamy pomiar trzykrotnie i obliczamy średnią wartość współczynnika załamania n.

Wartości pomiarowe dla wody destylowanej: stężenie c= 0

n_i=1,333

n_i=1,332 n średnie n=1,333

n_i=1,334

kąt graniczny
≈ 0,7502

Wartości pomiarowe dla gliceryny o stężeniu c = 0,050

n_i=1,339

n_i=1,340 n średnie n=1,339

n_i=1,339

kąt graniczny
≈ 0,7468

Wartości pomiarowe dla gliceryny o stężeniu c =0,100

n_i=1,346

n_i=1,347 n średnie n=1,347

n_i=1,347

kąt graniczny
≈ 0,7423

Wartości pomiarowe dla gliceryny o stężeniu c =0,150

n_i=1,356

n_i=1,355 n średnie n=1,356

n_i=1,356

kąt graniczny
≈ 0,7375

Wartości pomiarowe dla gliceryny o stężeniu c =0,200

n_i=1,357

n_i=1,356 n średnie n=1,357

n_i=1,358

kąt graniczny
≈ 0,7369

Wartości pomiarowe dla gliceryny o stężeniu c =0,250

n_i=1,360

n_i=1,361 n średnie n=1,361

n_i=1,361

kąt graniczny
≈ 0,7347

Wartości pomiarowe dla gliceryny o stężeniu c =0,300

n_i=1,365

n_i=1,366 n średnie n=1,366

n_i=1,366

kąt graniczny
≈ 0,7320

Wartości pomiarowe dla gliceryny o stężeniu c_x =?

n_i=1,360

n_i=1,361 n średnie n=1,361

n_i=1,361

kąt graniczny
≈ 0,7347

Rachunek błędów.

Stężenia roztworów c podane są z dokładnością Δc = 0,0025 g/cm³

Błąd pomiaru roztworu Δn :

Δn = maxn - n₁

dla wody destylowanej : Δn = 0,001

dla gliceryny o stężeniu c =0,050
: Δn= 0,001

dla gliceryny o stężeniu c =0,100
: Δn= 0,001

dla gliceryny o stężeniu c =0,150
: Δn= 0,001

dla gliceryny o stężeniu c =0,200
: Δn= 0,001

dla gliceryny o stężeniu c =0,250
: Δn= 0,001

dla gliceryny o stężeniu c =0,300
: Δn= 0,001

Wnioski:

Mierząc kąt graniczny padania w ośrodku 2 optycznie gęstszym, możemy ze wzoru ostatniego wyznaczyć jego współczynnik załamania n_2,1 względem ośrodka 1 optycznie rzadszego. A także znając bezwzględny współczynnik załamania jednego ośrodka można wyznaczyć bezwzględny współczynnik drugiego ośrodka . Zapoznaliśmy się także z obsługą i działaniem refraktometru Abbego. Dowiedliśmy także ,że kąt graniczny zależy od stężenia roztworu. Znając zależność między stężeniem , współczynnikem załamania i kątem granicznym można w przybliżeniu podać stężenie procentowe nieznanego roztworu . Takie doświadczenie są jednak opatrzone pewną dozą błędu pomiarowego wynikającego z niedokładnego oczyszczenia powierzchni pryzmatów, a także z niedość precyzyjnego ustawienia linii rozgraniczającej na przecięciu nitek pajęczych.

---